基于單頻GPS精密單點定位算法研究

陳 蕾，許文桓

（國核電力規劃設計研究院重慶有限公司，重慶 401121）

隨著人們對GPS定位精度要求的不斷提高，國內外學者已經給出了一些可能的靜動態的精密單點定位模型［1－4］，在這些定位模型中，為了減少觀測誤差和噪聲，消除電離層誤差的偽距和載波相位組合等方法經常用到，然而，這種方法不能保證載波相位的整周模糊度的整數性，這就降低了定位精度，而且這種算法只限于雙頻GPS。

本文提出了一種針對廉價的單頻GPS接收機新的精密單點定位算法，這種算法不需要偽距和載波相位觀測量的線性組合，這樣就保持了整周模糊度的整數性，提高了定位精度。在這個算法中，L1載波和基于C/A碼的偽距用新的GPS回歸方程和回歸矩陣進行描述，這些回歸方程和回歸矩陣作為單頻精密單點定位的觀測模型。由電離層延遲、對流層延遲、衛星軌道誤差、衛星鐘誤差和接收機鐘差引起的載波相位和基于C/A碼的偽距誤差，利用合適的誤差模型嵌入到回歸方程中，用最小二乘估計所有的未知參數，在估計的過程中，考慮觀測噪聲的隨機屬性，提高參數估計的可靠性和縮短收斂時間。此外，由于每一歷元的觀測數據都可以連續得到，這樣就可以應用卡爾曼濾波得到單頻精密單點定位回歸方程。

1 算法模型

1.1 單頻精密單點定位回歸方程

將L1載波相位和基于C/A碼的觀測定位數據公式［5－9］化為

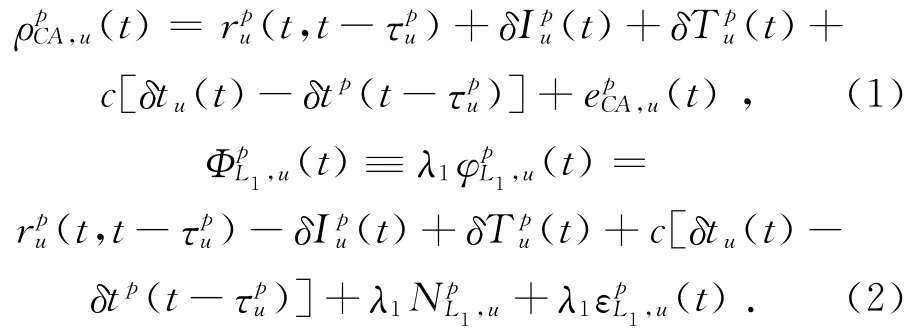
式中：u≡［xu，yu，zu］T為測站位置坐標向量；sp≡［xp，yp，zp］T為衛星P的坐標向量（t）為t時刻測站u到衛星P的偽距；（t）為t時刻L1載波的相位觀測值；τpu為測站u到衛星P的信號傳播時間；λ1：L1載波的波長，數值為0.190 3m；δIpu（t）、δTpu（t）為電離層、對流層延遲誤差；δtu（t）、δtp（tτpu）為接收機在t時刻和衛星在t－τpu時刻的鐘差；為L1載波的整周模糊度；為測量誤差；rpu（t，t－τpu）為t時刻測站到t－τpu時刻衛星P的幾何距離。

為了方便表示將

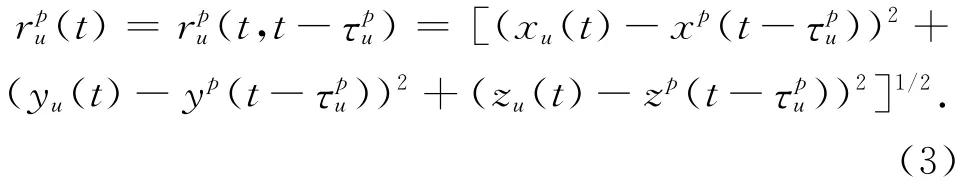
式中，衛星坐標xp，yp，zp可以通過導航電文得到，但包含有軌道誤差，本文通過衛星精密星歷軌道化消除了軌道誤差，達到了精密定位的精度。定義＾sp為已經計算出來的衛星的精確坐標，下面為了算法的簡捷敘述將t，t－τpu省略。

由導數關系可以得到

將式（3）在u＝，（j＝1），sp＝＾sp進行一階泰勒展開為

這樣式（1）和式（2）轉變為

式中：

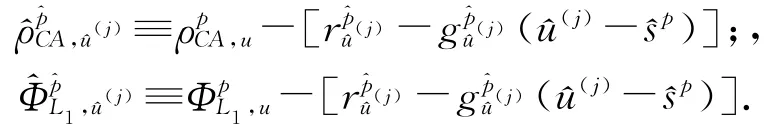
將式（6）和式（7）用向量矩陣表示為

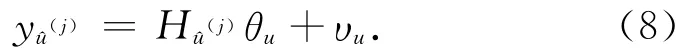
式中：

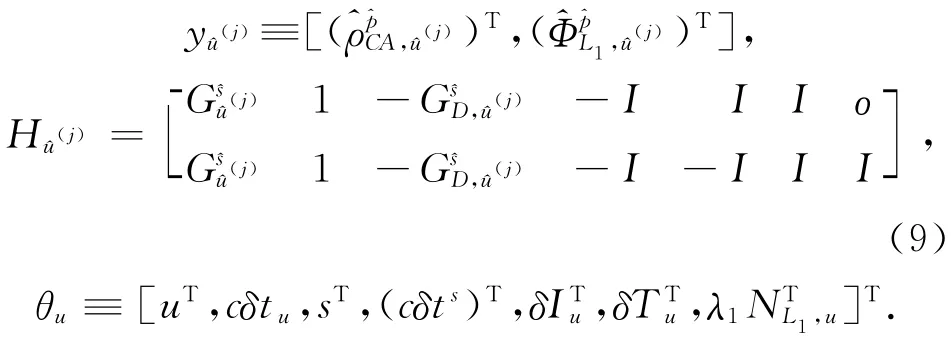
υu≡［，］T，I定 義為ns×ns單 位 矩陣，0定義為［1，1，…，1］T的ns×1向量。

為了得到θu的最小二乘估計，下面考慮未知參數和回歸方程的個數，從上述可以看出未知變量有4＋7ns個，即u：3，cδtu：1，s：3ns，cδts：ns，δIu：ns，δTu：ns，NL1，u：ns，而回歸方程個數為2ns，這樣就得不到θu的最小二乘解。如果已經計算出了衛星的位置坐標s，衛星鐘差cδts，電離層改正和對流層改正δIu，δTu。可得

此方程即為單頻GPS精密單點定位的觀測模型。式中：

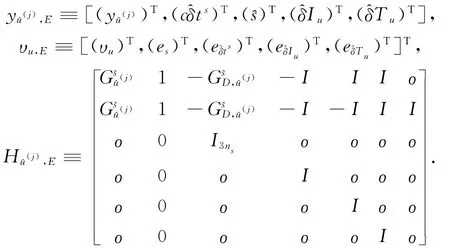
在這種情況下，回歸方程的個數為8ns，當ns≥4，8ns≥4＋7ns，這樣就可以計算出未知參數的準確值。當ns＜4時，系數矩陣H＾u（j），E是奇異的，這時不能夠得到θ的確切值。

對于式（10）來說，θu的最小二乘估計值是這樣得到的［10－11］：

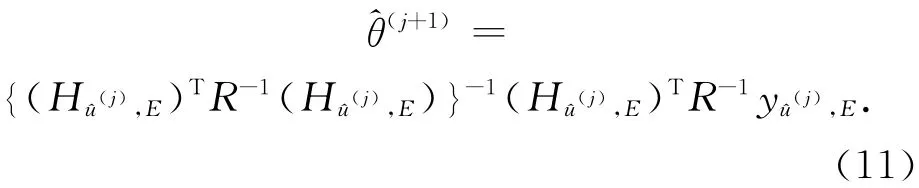
式中：R≡Cov［υu，E］，其誤差方差為

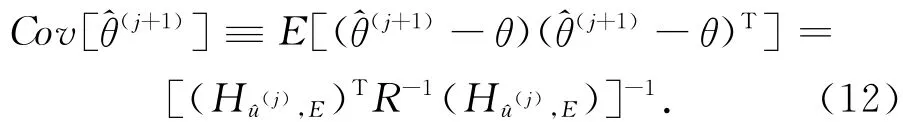
1.2 卡爾曼濾波應用于單頻精密單點定位

1.2.1 卡爾曼濾波的觀測方程

由式（10）可得

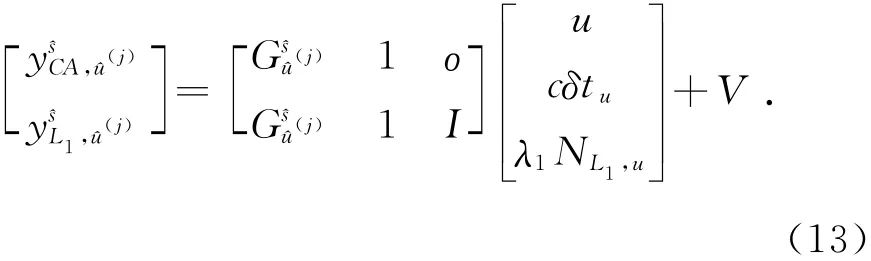
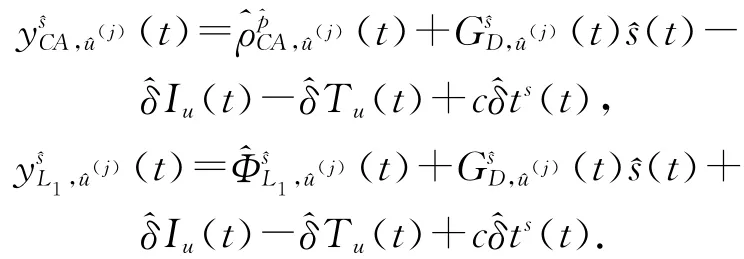
式（13）即為卡爾曼濾波的觀測方程。

1.2.2 狀態向量

在靜態定位時，點位的三維坐標、接收機鐘差和模糊度是必須要估計的，因此，定義靜態位置狀態向量

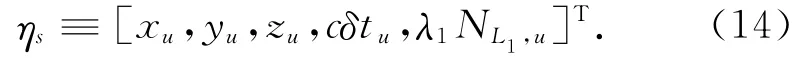
動態定位時，需要運動物體的數學模型，將接收機的速度假定為一階馬爾可夫過程［12－13］，因此，定義動態向量

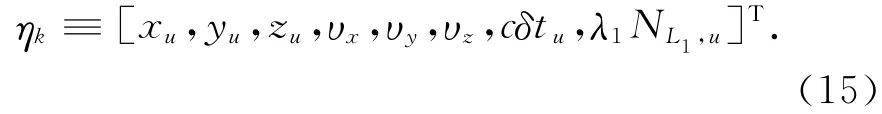
對于這2種情況，接收機鐘差cδtu也假定為一階馬爾可夫過程，可以得出下面的狀態方程：

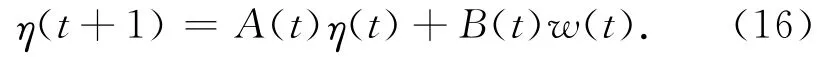
式中，狀態轉移矩陣為

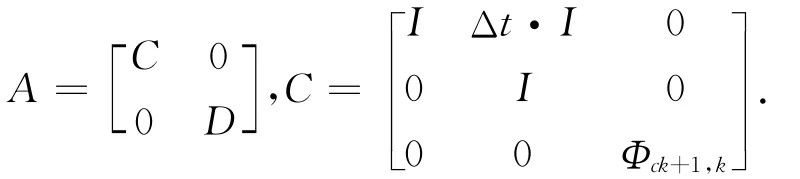
式中：I為3×3階單位矩陣，D為n維對角矩陣，對角元素取值為（2n－1）/（2n＋1），n＝100，Φck＋1，k＝為采樣率。

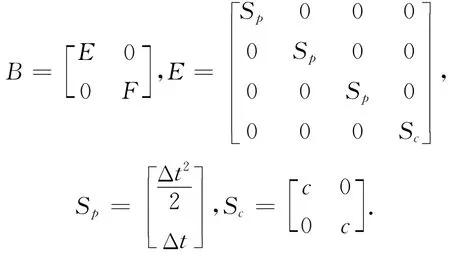
式中：F為n維對角矩陣，對角元素為：2n/（2n＋1），n＝100。w為系統噪聲，系統噪聲協方差矩陣為

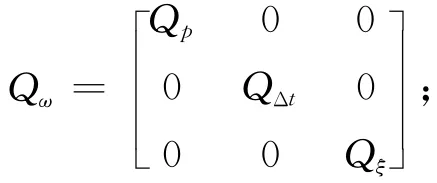
式中：Sdt，S˙dt參考Allan協方差參數［14］，Qξ為n維對角矩陣，對角元素取值為0.3P，P為用戶量程精度，可以從衛星星歷中求取。從式（13）和式（16）可見，觀測方程可以表示為

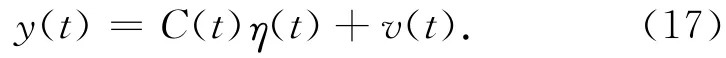
誤差

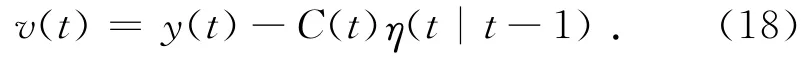
其協方差矩陣

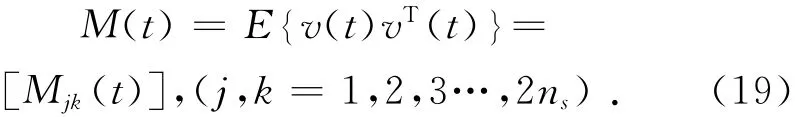
式中：P（t｜t－1）是濾波過程中η（t｜t－1）的方差矩陣，一般情況下v（t）是均值為0，方差為M（t）的白高斯噪聲［11］。

2 算例分析

實驗采用本文提出的單頻精密單點定位模型，GPS定位的所有誤差都必須考慮，主要通過2種途徑來解決：①對能精確模型化的誤差采用模型改正，如地球旋轉改正、相對論效應等都可以采用現有的模型精密改正。②對于不能精確模型化的誤差以參數形式進行估計，比如電離層延遲改正，目前還難以用模型精確模擬，則以參數對其進行估計。用載波相位變化率和切比雪夫多項式探測與修復周跳，用IGS網站提供的精密星歷對衛星軌道和衛星鐘差進行擬合求值。

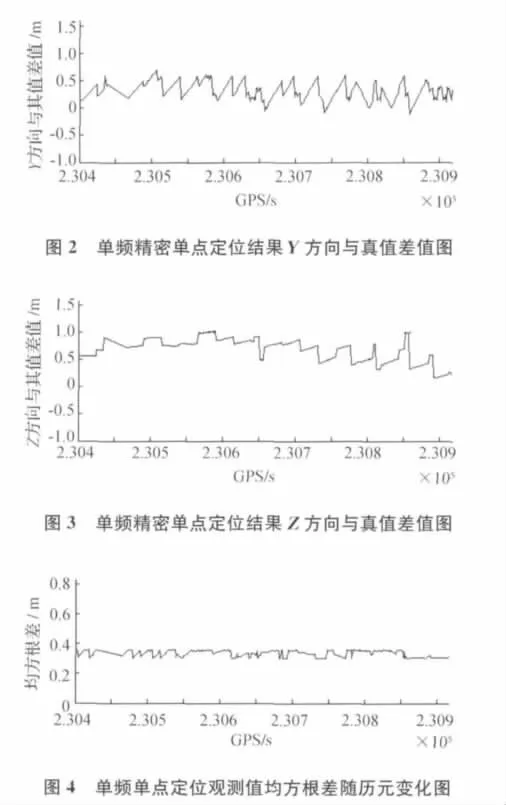
實驗用卡爾曼濾波對動態數據進行精密單點定位，采用數據為2008－03－11的觀測數據，采樣率為1s，觀測時衛星數目都在6～8顆，衛星截止高度角為10°，采用事后處理方式，實驗點的精確坐標前文已經敘述由差分載波相位模型精確得出。得到的單頻精密單點定位結果與實驗點的精確坐標進行對比，X，Y，Z坐標差如圖1、圖2、圖3所示，觀測值均方根差隨歷元變化，如圖4所示。

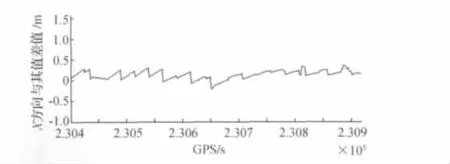
圖1 單頻精密單點定位結果X方向與真值差值圖

3 結 論

從上述圖中可以看出在Z方向比在水平X，Y方向有較大的偏差，Z方向收斂的時間大于水平方向。對于所有的數據單頻GPS精密單點定位能夠得到比較高的精度，而且定位結果比較穩定，在X方向的偏差小于50cm，在Y方向的偏差小于70cm，在Z方向的偏差小于1m，均方根在30～38cm之間。

［1］Sugimoto S，Kubo Y.GNSS Regressive Models and Precise Point Positioning，Proc.36th ISCIE International Symposium on Stochastic Systems Theory and its Applications，Oct.pp.159－164，2004［C］.Saitama：ISCIE，2004.

［2］Sugimoto S，Kubo Y.Carrier－Phase－Based Precise Point Positioning－a novel approach based on GNSS regression models，Proc.GNSS 2004 Symposium，Dec.P94，2004［C］.Sydney：GNSS，2004.

［3］Kubo Y，Kitao S，Fujita S，et al.A New RTK Algorithm for Carrier－Phase－Based Precise Point Positioning Based on GNSS Regression Models，Proc.18th Int.Tech.Meeting of the Satellite Division of The Institute of Navigation，Sep.pp.1492－1499，2005［C］.Long Beach，CA：ION GNSS，2005.

［4］Gao Y，Shen X.A New Method for Carrier－Phase－Based Precise Point Positioning［J］.Journal of The Institute of Navigation，2002，49（2）：109－116.

［5］Beran T，Kim D，Langley R B.High－Precision Single－Frequency GPS Point Positioning，Proc.16thInt.Tech.Meeting of the Satellite Division of The Institute of Navigation，Sep.pp.1192－1200，2003［C］.Portland，OR：ION GPS/GNSS，2003.

［6］Salam M A，Gao Y.Ambiguity Resolution in Precise Point Positioning：Preliminary Results，Proc.16th Int.Tech.Meeting of the Satellite Division of The Institute of Navigation，Sep.pp.1222－1228，2003［C］.Portland，OR：ION GPS/GNSS，2003.

［7］Le A Q.Achieving Decimetre Accuracy with Single Frequency Standalone GPS Positioning，Proc.17thInt.Tech.Meeting of the Satellite Division of The In－stitute of Navigation，Sep.pp.1881－1892，2004［C］.Long Beach，CA：ION GNSS，2004.

［8］Teunissen P J G，Kleusberg A（Eds.）.GPS for Geodesy［M］.2nd edition，Berlin：Springer－Verlag，1998.

［9］Leick A.GPS Satellite Surveying［M］.3rd edition，New York：Johon Wiley ＆Sons，2003.

［10］Sugimoto S，Kubo Y，Kumagai H.GPS Naviga－tion Algorithms and Estimation－Detection Theory，Systems，Control and Information［J］.ISCIE，2002，46（5）：276－285.

［11］Gelb A.Applied Optimal Estimation［M］.MIT Press，Massachusetts，1974.

［12］Uratani C，Sone K，Muto Y，et al.Dynamical Models for Carrier－Phase Kine－matic GPS Positioning，Proc.16th Int.Tech.Meeting of the Satellite Division of the Institute of Navigation，Sep.pp.809－818，2003［C］.Portland，OR：ION GPS/GNSS，2003.

［13］Muto Y，Kubo Y，Uratani C，et al.New Dynamical Models for Kinematic GPS Positioning，Proc.17th Int.Tech.Meeting of the Satellite Division of The Institute of Navigation，Sep.pp.2519－2528，2004［C］.Long Beach，CA：ION GNSS，2004.

［14］BROWN R G，HWANG PY C.Introduction to Random Signals and Applied Optimal Estimation［M］.2nded.New York：Wiley，1992.