半群DOn中理想的秩和相關(guān)秩
羅 永 貴
(貴州師范大學(xué) 數(shù)學(xué)與計算機科學(xué)學(xué)院, 貴陽 550001)
0 引 言
一個有限半群S的秩通常定義為rank(S)=min{A:A?S, 〈A〉=S}, 半群S及其子半群V之間的相關(guān)秩定義為
r(S,V)=min{A:A?S,A∩V=?, 〈A∪V〉=S}.
對于有限半群的秩及其相關(guān)秩的研究目前已有許多結(jié)果[1-10].
設(shè)[n]={1,2,3,…,n}(n≥3)并賦予自然數(shù)的大小序.Tn與Sn分別表示[n]上的全變換半群和對稱群, Singn=TnSn是[n]上的奇異變換半群. 設(shè)α∈Singn, 若對任意的x,y∈[n],x≤y?xα≤yα, 則稱α是保序的. 記On為[n]上的保序有限奇異變換半群. 若對任意的x,y∈[n],x≤y?xα≥yα, 則稱α是反序的. 記Dn為[n]上所有反序變換構(gòu)成的集合. 令DOn=On∪Dn. 顯然,DOn是Singn的子半群, 稱為保反序有限奇異變換半群. 記
LD(n,r)={α∈DOn: Imα≤r} (1≤r≤n-1),
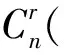
本文在文獻[1-3]的基礎(chǔ)上考慮保反序有限奇異變換半群DOn的雙邊理想LD(n,r)的秩及其相關(guān)秩, 證明了如下結(jié)果:
定理1設(shè)n≥3, 1≤r≤n-1, 則Jr是LD(n,r)的生成集, 即LD(n,r)=〈Jr〉.
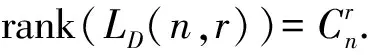
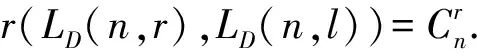
1 預(yù)備知識
設(shè)P,Q是自然序集[n]的非空子集, 若對任意的a∈P,b∈Q有a Kerα={(x,y)∈[n]×[n]:xα=yα}, 對任意的t∈Imα,tα-1表示t的原象集. 設(shè)α∈LD(n,r), 如果x 其中每個Ai(i=1,2,…,k-1,k)都是凸集, 并且A1 為敘述方便, 這里引用Green-等價關(guān)系[11]. 文獻[3]對半群LD(n,r)的L,R,J有如下刻劃: 對任意的α,β∈LD(n,r), (α,β)∈L ? Imα=Imβ, (α,β)∈R ? Kerα=Kerβ, (α,β)∈J ? Imα=Imβ. LD(n,1)?LD(n,2)?…?LD(n,n-2)?LD(n,n-1)=DOn. 本文未定義的術(shù)語及符號參見文獻[12-17]. 引理1J1?J2·J2. 情形1) 若a=1, 令 則β,γ∈J2且α=βγ. 情形2) 若a=n, 令 則β,γ∈J2且α=βγ. 情形3) 若1 則β,γ∈J2且α=βγ. 引理2對2≤k≤r-1, 2≤r≤n-1, 有Jk?Jk+1·Jk+1. 證明: 對任意的α∈Jk, 設(shè)α的標準表示為 這里每個Ai(i=1,2,…,k-1,k)都是凸集, 并且A1 由于2≤k≤r-1≤n-2, 因此必存在i∈{1,2,…,k-1,k}, 使得Ai≥2. 若α是保序的, 則記x=minAi; 若α是反序的, 則記x=maxAi. 下面分3種情形證明存在β,γ∈Jk+1, 使得α=βγ. 情形1) 若a1≠1, 令 則β,γ∈Jk+1且α=βγ. 情形2) 若ak≠n, 令 則β,γ∈Jk+1且α=βγ. 情形3) 若a1=1且ak=n, 結(jié)合2≤k≤n-2知, 存在j∈{2,3,…,k-1,k}, 使得aj-aj-1>1. ① 如果i 則β,γ∈Jk+1且α=βγ. ② 如果i=j, 令 則β,γ∈Jk+1且α=βγ. ③ 如果i>j, 令 則β,γ∈Jk+1且α=βγ. 由引理1和引理2可知, 對任意的α∈LD(n,r)都可以表示為LD(n,r)的頂端J-類Jr中秩為r的元素的乘積或α∈Jr. 即Jr是LD(n,r)的生成集,LD(n,r)=〈Jr〉. 引理3設(shè)α,β∈LD(n,r), 若(α,β),(α,αβ)∈J, 則(αβ,β)∈L, (α,αβ)∈R. 證明: 設(shè)α,β∈LD(n,r), 若(α,β),(α,αβ)∈J, 則Imα=Imβ=Im(αβ). 再由Im(αβ)?Imβ, Kerα?Ker(αβ)與Xn的有限性知, Im(αβ)=Imβ, Kerα=Ker(αβ), 即(αβ,β)∈L, (α,αβ)∈R. 注意到當(dāng)r=1時, J1中共有n個L-類和1個R-類, 且每個H=R∩L僅有一個保序的元素, 因此, 有: 推論2設(shè)自然數(shù)n≥3, 則rank(LD(n,1))=n. 2) 這m個冪等元都是保序變換. 其次, 對任意的α∈Jr, 分兩種情形驗證α∈〈M〉, 即Jr?〈M〉. 1) 若存在i,j∈{1,2,…,m-1,m}, 使得Kerα=Kerαi, Imα=Imαj. ① 若α是保序的, 則當(dāng)i α=αiαi+1…αm-1αmα1α2α3…αi-1αi…αm-1αm; 當(dāng)i=j=m時, 有α=αmα1α2α3…αm-1αm; 當(dāng)i=j α=αiαi+1…αm-1αmα1α2α3…αi-1αiαi+1…αm-1αmα1α2…αj-1αj. ② 若α是反序的, 則當(dāng)i α=αiαi+1…αj-1αj…αm-1αmα1α2…αi-1αiαi+1…αj-1αj; 當(dāng)i α=αiαi+1…αm-1αmα1α2…αi-1αi; 當(dāng)i>j時, 有α=αiαi+1…αm-1αmα1α2…αj-1αj. ① 若α是保序的, 則當(dāng)j=1時, 有β=βi; 當(dāng)2≤j≤m時, 有 α=αjαj+1…αm-1αmα1α2…αj-1αjαj+1…αm-1αmβi. ② 若α是反序的, 則當(dāng)1≤j≤m時, 有α=αjαj+1…αm-1αmβi. 當(dāng)1≤l [1] Gomes G M S, Howie J M. On the Ranks of Certain Semigroups of Order-Preserving Transformations [J]. Semigroup Forum, 1992, 45(1): 272-282. [2] Garba G U. On the Idempotent Ranks of Certain Semigroups of Order-Preserving Transformations [J]. Portugaliae Mathematica, 1994, 51(2): 185-204. [3] Fernandes V H, Gomes G M S, Manuel M J. Congruences On Monoids of Order-Preserving or Order-Reversing Transformations on a Finite Chain [J]. Glasgow Mathematical Journal, 2005, 47: 413-424. [4] Howie J M. Idempotent Generators in Finite Full Transformation Semigroups [J]. Proceedings of the Royal Society of Edinburgh: Sect A Math, 1978, 81(3/4): 317-323. [5] Howie J M, McFadden R B. Idempotent Rank in Finite Full Transformation Semigroups [J]. Proceedings of the Royal Society of Edinburgh: Sect A Math, 1990, 114(3/4): 161-167. [6] Howie J M, Ruskuc N, Higgins P M. On Relative Ranks of Full Transformation Semigroups [J]. Communication in Algebra, 1998, 26: 733-748. [7] Umar A. On the Semigroups of Order-Decreasing Finite Full Transformations [J]. Proceedings of the Royal Society of Edinburgh: Sect A Math, 1992, 120(1/2): 129-142. [8] Umar A. On the Ranks of Certain Finite Semigroups of Order-Decreasing Transformations [J]. Portugaliae Mathematica, 1996, 53(1): 23-34. [9] ZHAO Ping, YOU Tai-jie, XU Bo. Idempotent Rank of SemigroupPC(n,r) [J]. Journal of Jilin University: Science Edition, 2012, 50(1): 44-48. (趙平, 游泰杰, 徐波. 半群PC(n,r) 的冪等元秩 [J]. 吉林大學(xué)學(xué)報: 理學(xué)版, 2012, 50(1): 44-48.) [10] XU Bo, ZHAO Ping. Maximal Subsemibands of the SemigroupPOn[J]. Journal of Jilin University: Science Edition, 2012, 50(3): 445-451. (徐波, 趙平. 半群POn的極大子半帶 [J]. 吉林大學(xué)學(xué)報: 理學(xué)版, 2012, 50(3): 445-451.) [11] Green J A. On the Structure of Semigroups [J]. The Ann of Math, 1951, 54(1): 163-172. [12] Clifford H, Preston G B. The Algebraic Theory of Semigroups [M]. Providence: Amer Math Soc, 1961. [13] Howie J M. An Introduction to Semigroup Theory [M]. London: Academic Press, 1976. [14] Higgins P M. Techniques of Semigroup Theory [M]. New York: Oxford University Press, 1992. [15] Howie J M. Fundamentals of Semigroup Theory [M]. Oxford: Oxford University Press, 1996. [16] Ganyushkin O, Mazorchuk V. Classical Finite Transformation Semigroups [M]. London: Springer, 2009. [17] Nikola Ruskuc. Semigroup Presentations [D]. St Andrews, Scotland: University of St Andrews, 1995.
2 定理的證明
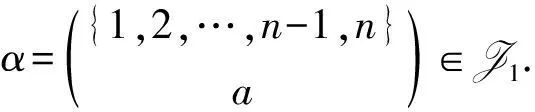
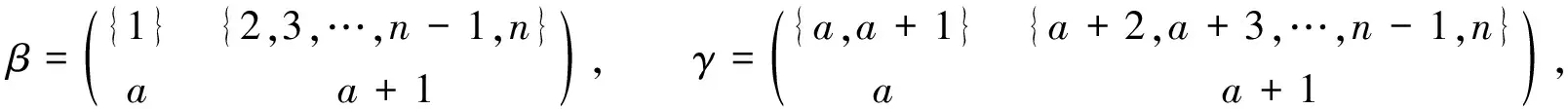
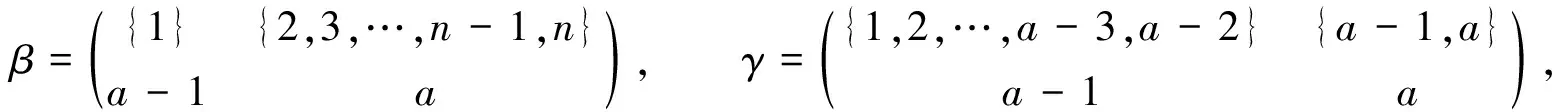
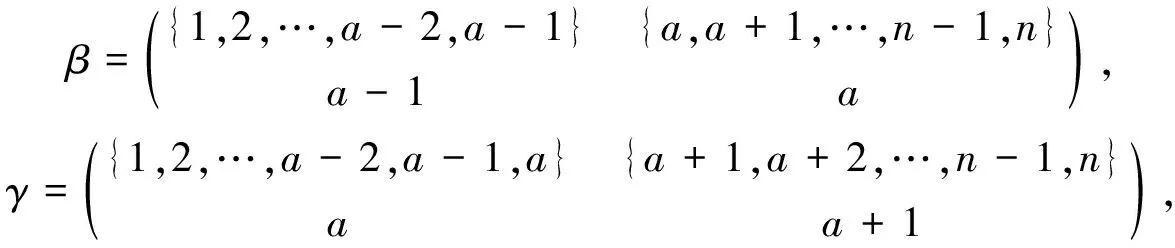
2.1 定理1的證明
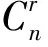
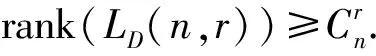
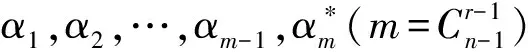
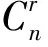
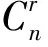
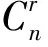
2.2 定理2的證明
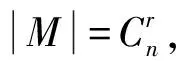
2.3 定理3的證明


