高樁式LNG全容罐的地震作用計算

宋延杰 李金光 鄭建華

中國寰球工程公司 北京 100029

全容式LNG儲罐的基礎形式有高樁式基礎、地面式基礎、樁式地面基礎和板式高承臺基礎等多種形式。儲罐采用何種形式的基礎與場地的地質條件、地質環境、地震及冷量消散方式等諸多因素有關。目前國內外已建或在建的全容式LNG儲罐最常采用的基礎形式是高樁式基礎。

對全容式LNG儲罐進行地震作用計算是LNG儲罐設計建造的一項重要內容，不僅有正常操作基準地震(OBE)作用計算，還有安全停運地震(SSE)作用計算。其中，操作基準地震是指設施在其設計壽命期內可承受的可能發生的地震，安全停運地震是在設施所在地罕見的強烈地震[1,2]。高樁式LNG全容罐不僅是固-液同時作用的結構設施，且基礎形式還較為復雜，需考慮樁-土間的相互作用。在地震作用下，儲罐設施中的內罐和外罐各自的動力反應如何？樁頭的地震作用力多大，能否滿足承載力要求？這些都是儲罐工程設計中需要考慮的地方。本文以某實際工程項目的高樁式LNG全容罐為例，對其在地震作用下的效應進行計算分析，為樁基方案的確定提供了依據。

1 地震作用計算要點

1.1 內罐液體在地震作用下的效應計算

內罐液體在地震作用下的效應分為液體沖擊作用對罐體產生的動壓力和液體晃動作用對罐體產生的動壓力。通常，液體的晃動周期比較長(一般為10s左右)，在該周期處，加速度已非常小，這樣晃動作用產生的動壓力就很小；另一方面，液體晃動作用和沖擊作用不會同時出現，根據SRSS組合規則，晃動作用的影響將會更小，在實際計算中可忽略不計。這樣，在水平地震作用計算中，僅計算沖擊作用產生的動壓力即可。

由Housner理論可知，當儲罐受到來自罐底的水平加速度a1(t)作用時，作用于罐壁上任一點(θ，z)處的液體沖擊動壓力為[3，4]：

(1)

式中，a1(t)為水平加速度，m/s2；ρ為儲液罐中液體的密度，kg/m3；r為儲液罐半徑，m；h為液位高，m；θ為任意一點沿圓周方向的方位角，rad；z為該點距底板的高度，m；其坐標及參數符號見圖1。

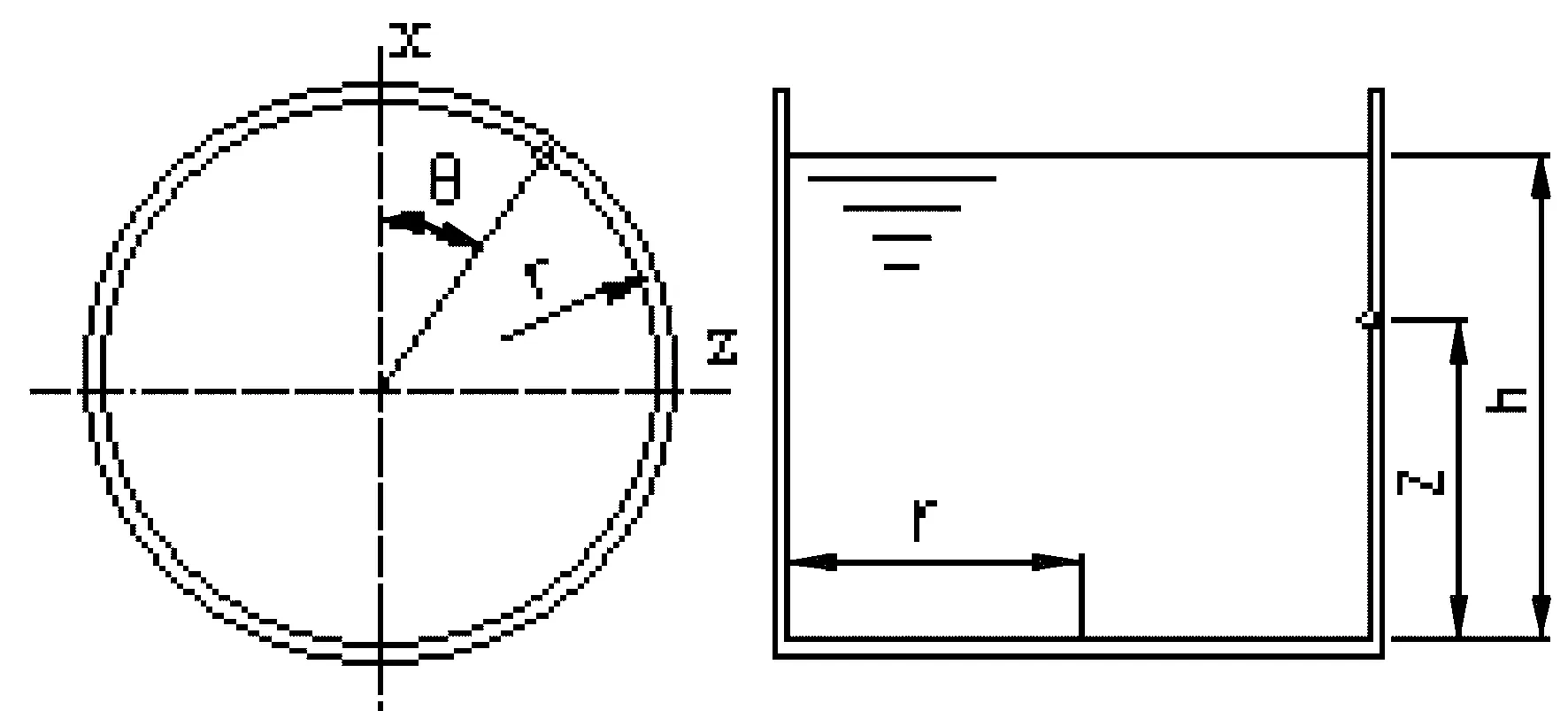
圖1 儲罐坐標及參數符號示意圖

1.2 計算模型

內罐的地震作用計算采用附加質量法計算模型[5]。附加質量法是一種計算液固耦合問題的近似方法，其基本思路是把液體對罐壁某點處的沖擊動壓力等效為與該點一起運動的附加質量對該點的慣性力，通過施加附加質量于內罐罐壁來模擬液體的沖擊作用，該計算模型使得計算解耦，從而減少了計算量。

根據式(1)的動壓力計算公式，可推導出某位置處的附加質量為：

(2)

附加質量沿罐壁環向的分布形式見圖2。

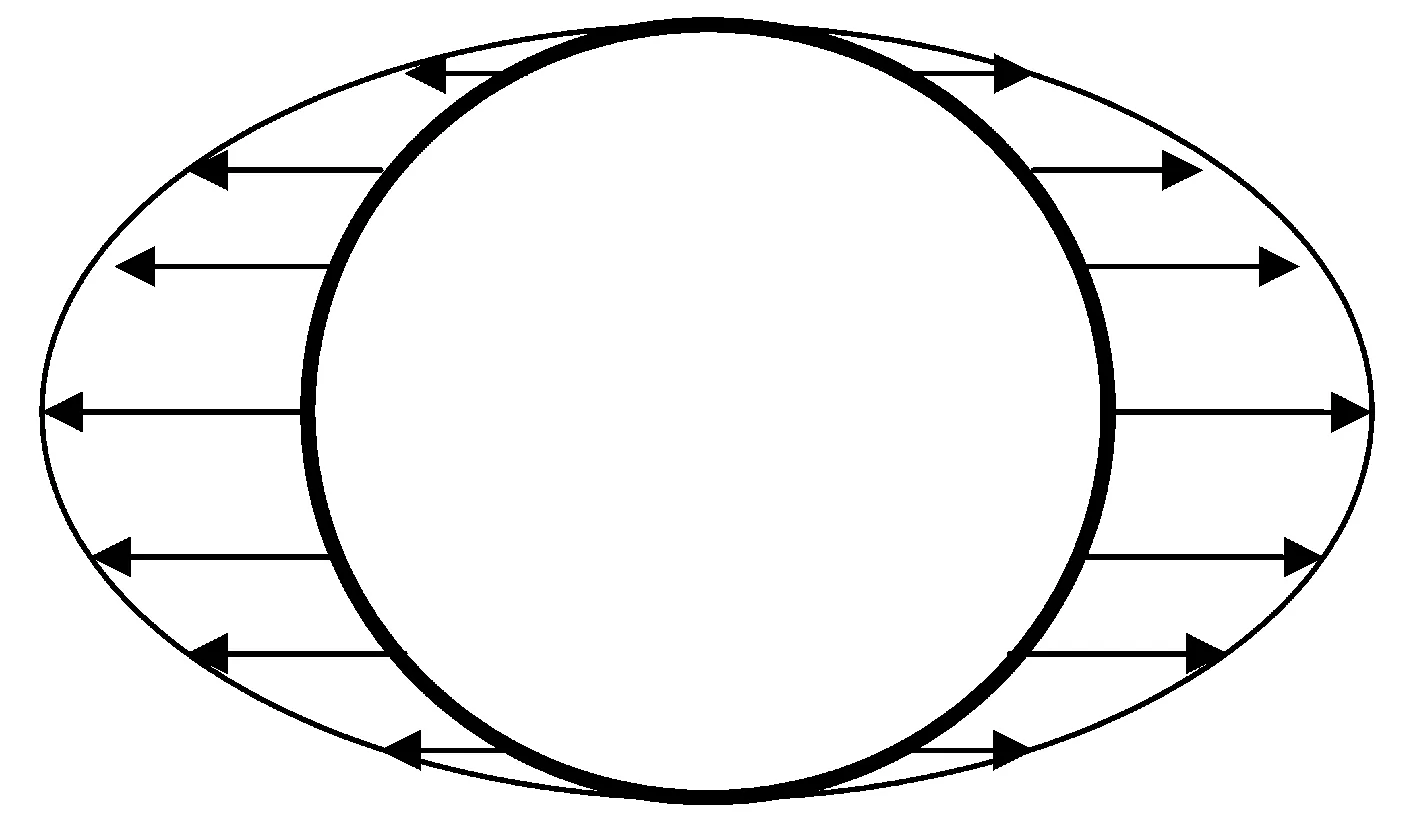
圖2 附加質量沿環向分布示意圖

可見，θ為0處的附加質量是最大值，并且附加質量關于加速度方向以及與加速度方向垂直方向的分布都對稱。

外罐是實體混凝土結構，采用殼單元按實際尺寸來模擬其質量和剛度分布。儲罐地震作用是一種動力作用，其結果跟質量和剛度相關，而保冷層等輔助材料的質量很小，剛度更軟，對整個結構的動力反應影響很小，因此，在建立計算模型時不需將這些材料建立幾何單元到模型中，只需將它們的質量附加到外罐模型中，考慮質量影響而忽略其剛度的影響。

對于高樁式基礎，其地面以上的樁用梁單元來模擬；地面以下的樁，用彈性嵌固模型來模擬，即在每根樁的地面位置處用水平彈簧單元來模擬土體對樁的水平約束，用豎向彈簧單元來模擬土體對樁的豎向約束，用轉動彈簧單元來模擬土體對樁的抗彎約束。

高樁式LNG全容罐的地震作用計算模型見圖3。

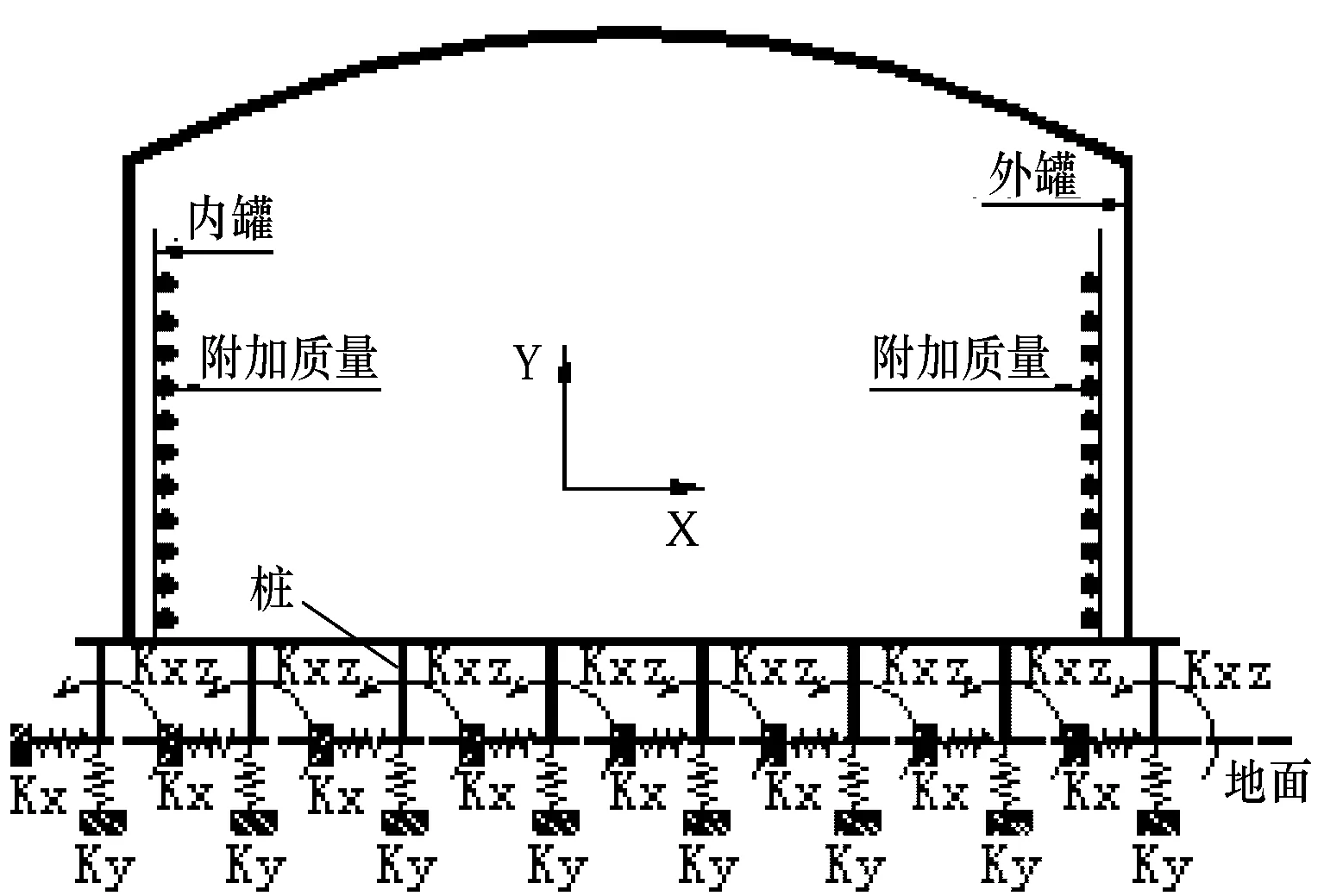
圖3 高樁式LNG全容罐的地震作用計算模型

1.3 計算步驟

LNG全容罐的地震作用計算應分三步進行：

1.3.1 模態分析

該分析步進行模態計算，得到LNG儲罐在空罐和滿罐兩種工況下的振型和頻率。

1.3.2 反應譜分析

該分析步根據第一步計算得到的振型和頻率，再結合地震加速度反應譜進行反應譜分析，得到LNG儲罐的地震作用效應。用平方和平方根方法(SRSS)來組合各個振型的結果作為輸出結果。

1.3.3 效應組合

根據參考文獻6的4.3.3.5節要求，水平地震與豎向地震同時作用時采用一方效應100%參與組合，另一方效應30%參與組合的線性組合方式，具體見表1。

表1 效應組合規則

2 計算實例

2.1 基本參數

以某1.6×105m3高樁式LNG全容罐為例，其基本形狀見圖4。

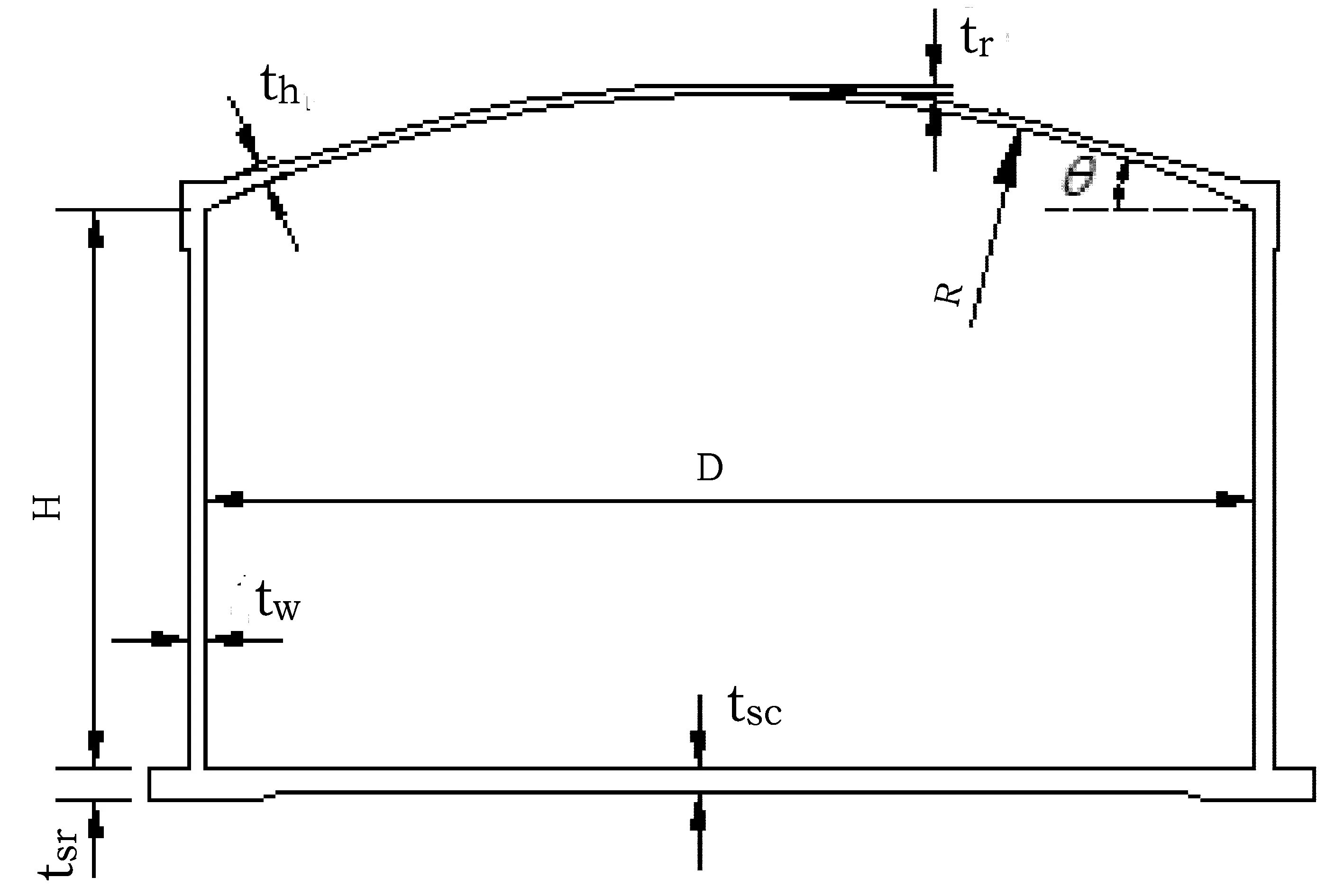
圖4 高樁式LNG全容罐的基本幾何尺寸

外罐內直徑D=82m，罐壁高度H=38.55m，壁厚tw=0.8m，罐頂厚度中心tr=0.4m，罐頂腋部厚度th=0.8m，罐頂半徑R=82m，底板中心厚度tsc=0.9m，底板邊緣厚度tsr=1.2m；C50混凝土密度ρc=2500kg/m3；內罐泄漏后的液位HL=33.3m，液體密度ρL=480kg/m3，蒸汽壓力qv=29kPa；OBE地震作用時，土體對地面以下樁的水平約束Kx=Kz=1.61×108N/m，豎向約束Ky=1.28×109N/m，抗彎約束Kxz=Kzx=4.67×108N·m/rad，SSE地震作用時，土體對地面以下樁的水平約束Kx=Kz=9.45×107N/m，豎向約束Ky=1.28×109N/m，抗彎約束Kxz=Kzx=3.27×108N·m/rad。

2.2 荷載簡化

內罐罐壁自重和彈性毯自重簡化為集中荷載施加到底板上；珍珠巖保冷層自重、內罐底板自重和附于底板上的材料(保溫材料、混凝土)自重簡化為面荷載施加到底板上；抗壓環自重、鋼罐頂自重和吊頂及吊頂保溫材料自重簡化為集中荷載施加到罐壁上。

2.3 反應譜

反應譜參數取自現場地震評估報告，5%阻尼比的反應譜計算公式：

Sa(T)=Amaxβ(T)

αmax=Amaxβmax

式中，Amax是最大水平地面加速度，m/s2；β(T)是地面加速度譜乘數；αmax是最大地震影響系數。其中：

水平地震加速度和相關反應譜參數見表2。

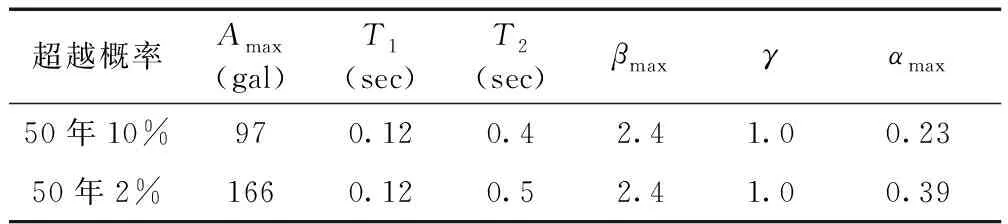
表2 水平地震加速度和相關反應譜參數

根據參考文獻2的定義，取50年10%的參數作為OBE地震條件，50年2%的參數作為SSE地震條件，這樣可以得到以下兩計算式。

(1)OBE- 水平地震：

(2)SSE- 水平地震：

OBE、SSE水平地震反應譜圖形形式見5。

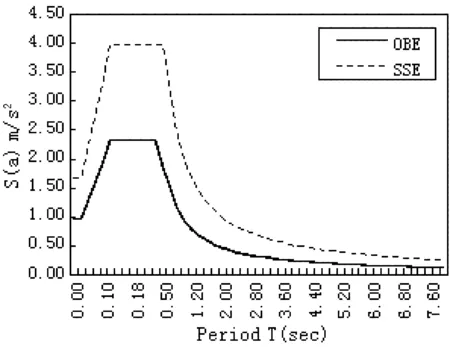
圖5 OBE、SSE水平地震反應譜

豎向地震反應譜取相應水平地震反應譜最大值的65%[7]。

3 有限元分析

3.1 有限元模型

高樁式LNG全容罐的地震計算模型采用三維有限元模型，由于結構和邊界條件的對稱性，取一半實體模型來進行網格劃分，計算模型見圖6。其中，外罐部分的節點數為30982，單元數為32709；內罐罐壁的節點數為2938，單元數為2800；每層內罐加強圈的節點數為452，單元數為336；樁的節點數為1800，單元數為1620。內罐液體為空時，儲罐模型總質量為2.378×107kg；內罐液體盛滿時，儲罐模型總質量為4.266×107kg。

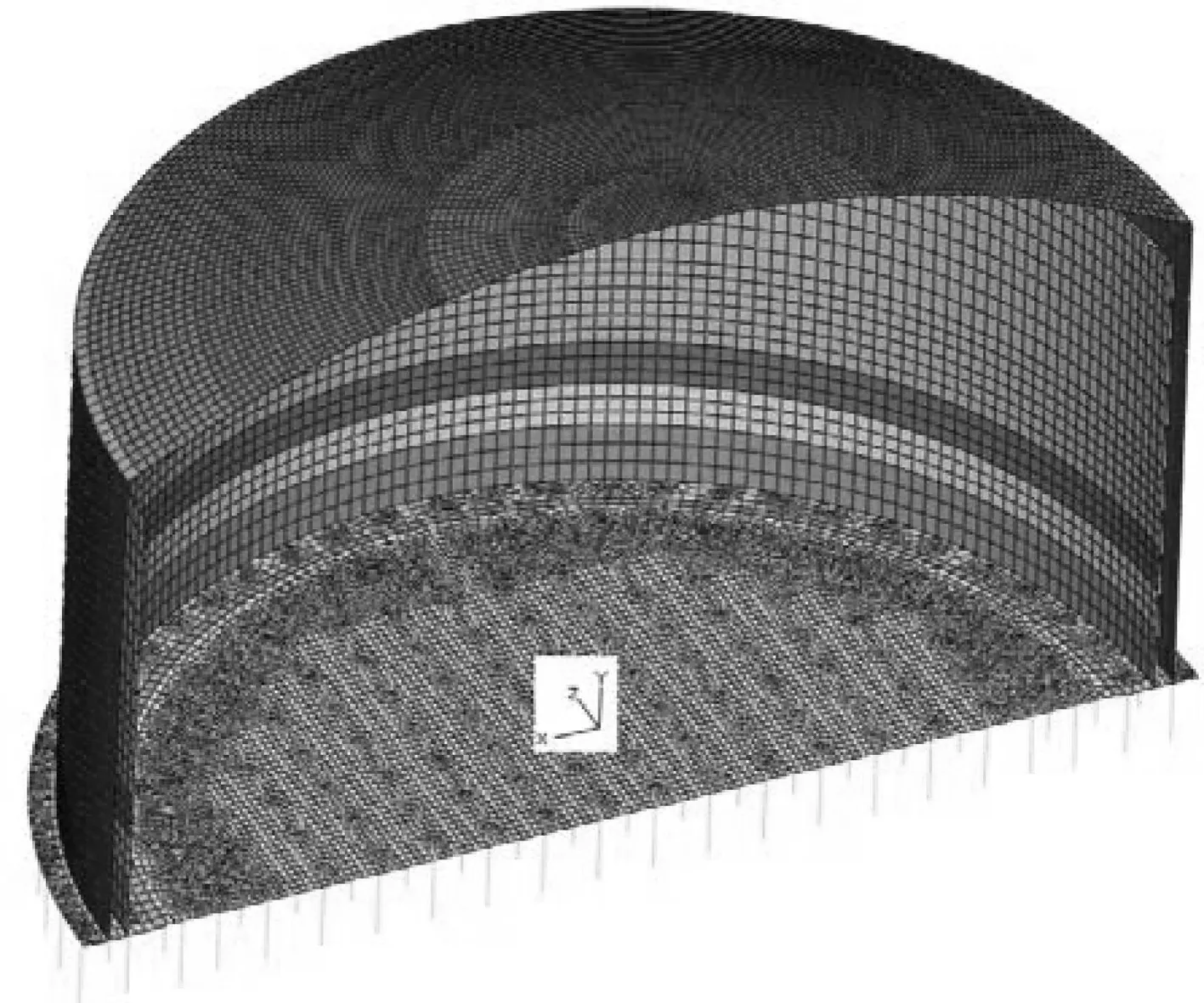
圖6 儲罐三維有限元模型

3.2 計算結果

3.2.1 模態分析計算結果

(1)內罐液體為空時的周期和參振質量見表3。

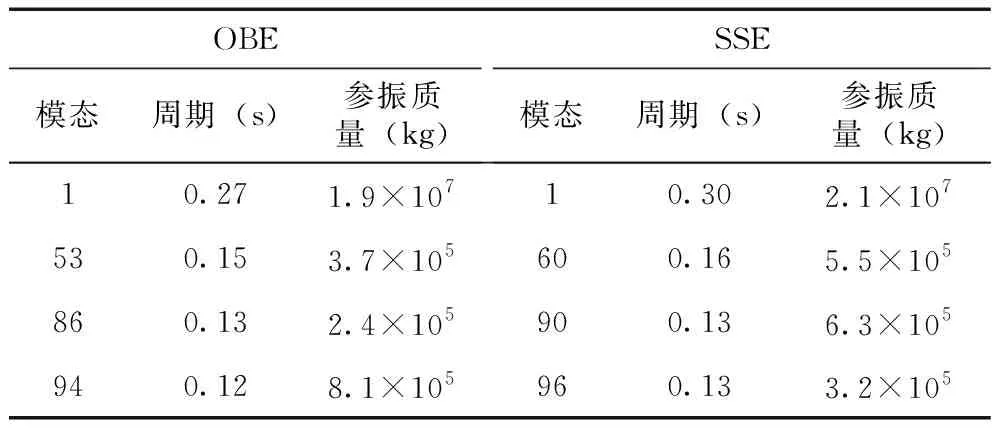
表3 空罐時模型周期和參振質量

空罐時OBE、SSE條件下的模態形狀見圖7～圖10。

圖7 OBE條件下第1階/第53階模態

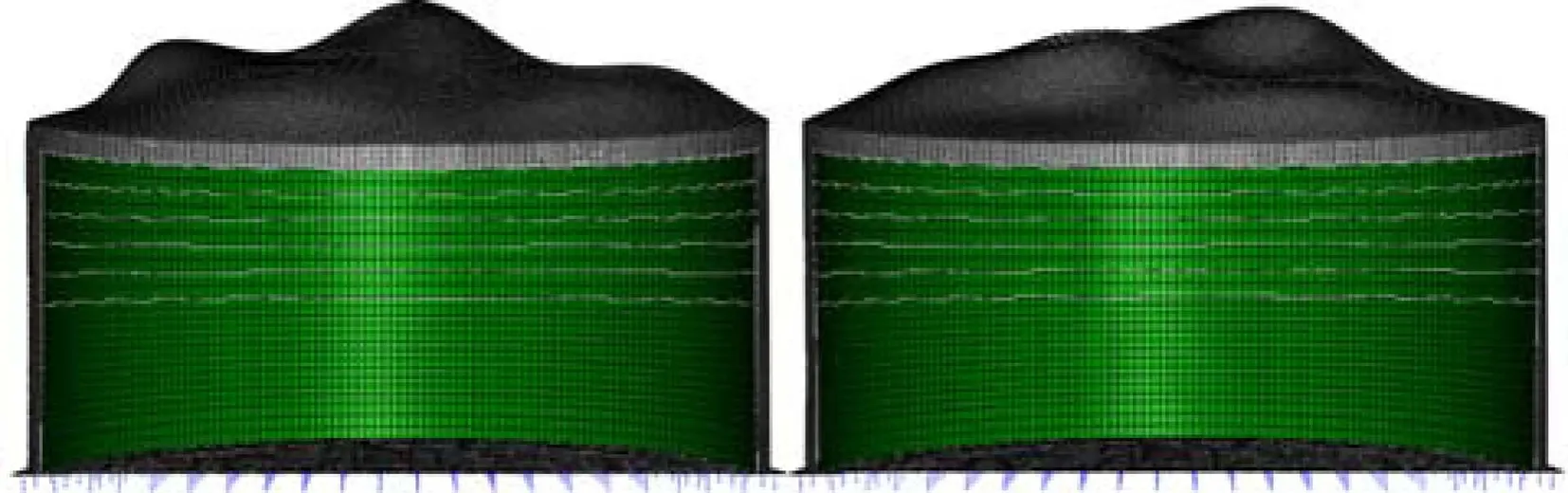
圖8 OBE條件下第86階/第94階模態

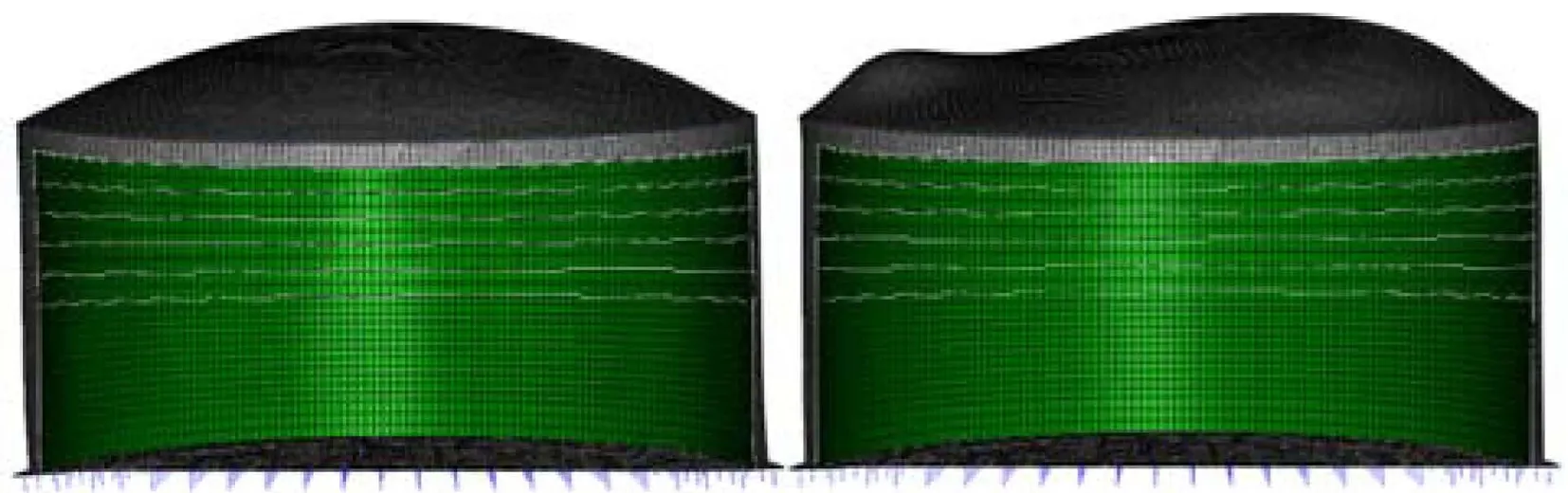
圖9 SSE條件下第1階/第60階模態

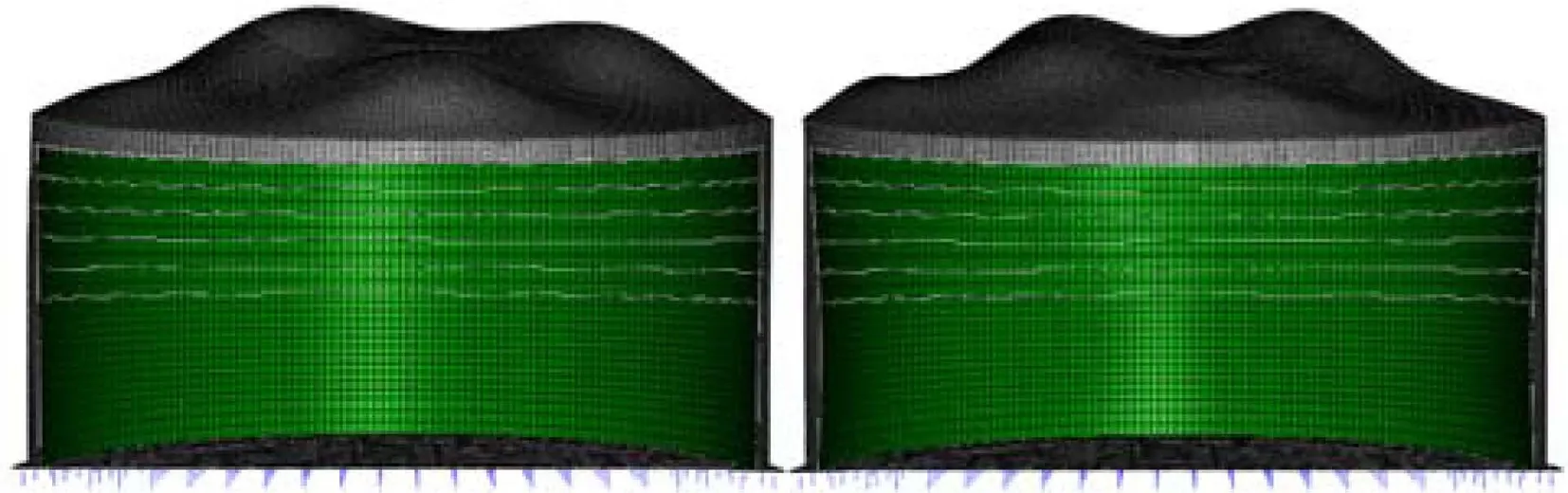
圖10 SSE條件下第90階/第96階模態

(2)內罐液體盛滿時的周期和參振質量見表4。

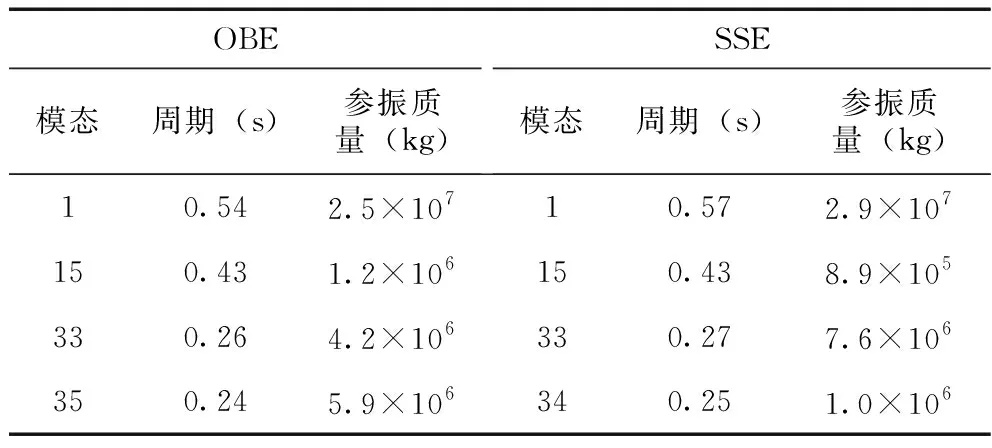
表4 滿罐時模型周期和參振質量

滿罐時OBE、SSE條件下的模態形狀見圖11～圖14。

圖11 OBE條件下第1階/第15階模態

圖12 OBE條件下第33階/第35階模態

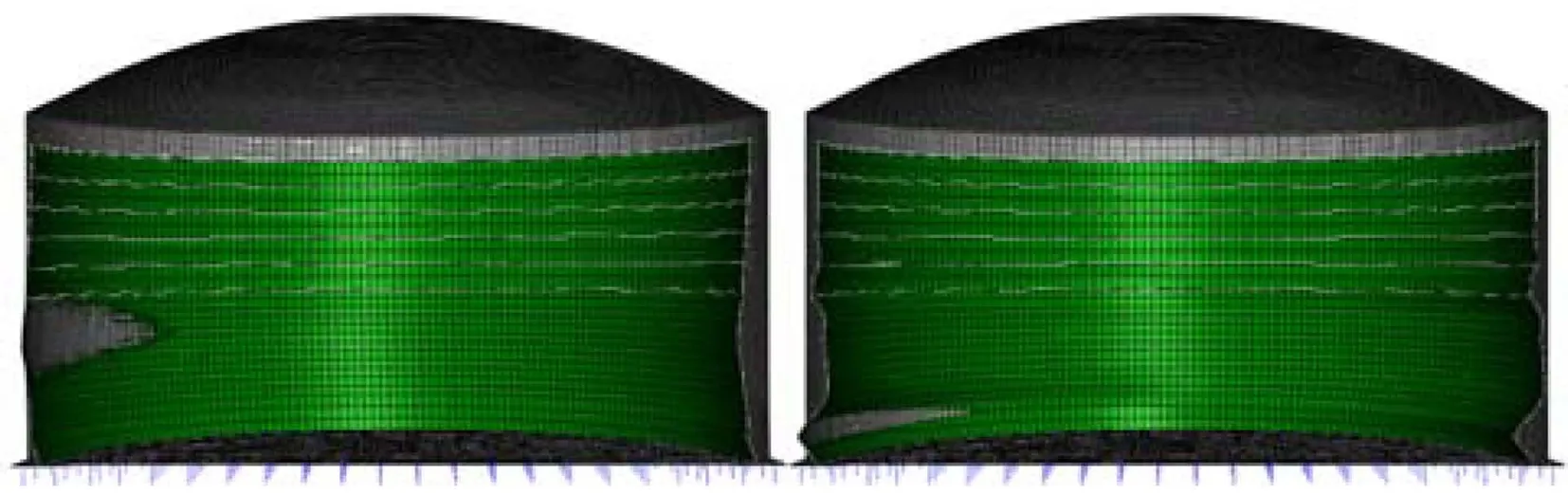
圖13 SSE條件下第1階/第15階模態

圖14 SSE條件下第33階/第34階模態

3.2.2 樁頂作用力組合結果

根據反應譜分析得到的水平地震作用應和豎向地震作用及自重作用按表1進行組合，得到地震作用時的最不利結果，以此來檢驗樁的水平承載力和豎向承載力能否滿足要求。豎向地震作用的計算根據規范的要求，等于水平向反應譜最大值的65%乘以重力荷載代表值[7]。

(1)空罐-OBE組合工況下最值統計見表5。

表5 空罐-OBE組合值 (t)

注：G為自重作用，H為水平地震作用，V為豎向地震作用。

(2)空罐-SSE組合工況下最值統計見表6。

表6 空罐-SSE組合值 (t)

(3)滿罐-OBE組合工況下最值統計見表7。

表7 滿罐-OBE組合值 (t)

(4)滿罐-SSE組合工況下最值統計見表8。

表8 滿罐-SSE組合值 (t)

根據樁基試樁報告，OBE狀態時，樁的水平承載力為60t；SSE狀態時，樁的水平承載力為105t；樁的豎向承載力為1800t。從表5～表8可知，樁的水平承載力和豎向承載力均能滿足要求。

4 結語

(1)由于高樁群的側向剛度相對于儲罐上部結構較小，因此罐體結構的主振型表現為罐內液體與混凝土外罐的同向位移，但參振質量主要是內罐液體沖擊質量，外罐只有少許質量參與該振型。

(2)當高樁群的側向剛度減小時，主振型的周期變長、參振質量變大；當高樁群的側向剛度增大時，主振型的周期變短、參振質量變小。

(3)從模態分析結果可知，高樁式LNG儲罐主振型的參振質量占總質量的比重較大，起控制作用，其它振型的參振質量較小，影響也較小。

(4)采用液體附加質量模型和樁基彈性嵌固模型建立的高樁式LNG儲罐地震作用計算模型，既能有效模擬內罐液體的動力效應，又能合理地考慮樁土間的相互作用，較好地反應高樁式LNG儲罐的整體動力特性。

(5)算例中樁頂的最不利荷載組合結果表明，樁的水平承載力和豎向承載力均能夠滿足儲罐的地震作用效應，樁基的設計方案是可行的。

參 考 文 獻

1 GB/T 20368-2006 , 液化天然氣(LNG)生產,儲存和裝運[S].

2 NFPA 59A-2006, Standard for the Production, Storage, and Handling of Liquefied Natural Gas (LNG) [S].

3 G.W.Housner,Dynamic Pressures on Accelerated Fluid Containers [J].Bull.Seismi.Soc.Am,1957,47(1):15-35.

4 Sudhir K Jain, O. R. Jaiswal, Modified proposed provisions for aseismic design of liquid storage tanks: Part I - codal provisions, Journal of Structural Engineering, Vol. 32, No.3, August-September 2005 pp. 195-206.

5 鄭建華,李金光,李艷輝.全容式LNG儲罐的地震作用計算模型研究 [J].化工設計,2012, 22(2): 11-14.

6 EN1998-1：2004, Design of structures for earthquake resistance - Part 1: General rules, seismic actions and rules for buildings.

7 GB 50011-2010, 建筑抗震設計規范[S].