近地面強風不同間隔滑動平均統計特性的對比分析

史文海，李正農，吳建佳

（1.溫州大學 建筑與土木工程學院，浙江 溫州 325035；2.湖南大學 土木工程學院，湖南 長沙 410082）

0 引 言

風荷載是作用于工程結構上的主要載荷之一，只有比較準確地了解強風的特性及其變化規律，在估算風對結構的作用和進行風場模擬時才可能有較高的精度。近年來，我國許多學者在上海、廣東和浙江等省開展了大量的近地邊界層風場特性的實測研究，取得了較為豐碩的研究成果［1－15］。

在對風場特性進行統計分析時，我國普遍采用10min時距［7－8］，且眾多的研究者在進行風場特性分析時都采用10min離散平均的方式計算出相應的風場特性。然而，目前對風場數據處理方法的研究還較少，基于10min離散平均的統計分析方法對實測數據的利用遠不充分，其結果不能很好的反映出風場的脈動性和變化規律，尤其是在實測風場數據較少的時候缺陷尤為明顯。

文中基于兩次臺風風場的實測數據，以3s、10s、1min和10min為間隔，進行了強風特性的10min滑動平均統計特性對比分析，以期獲得對近地面強風風場特性及其數據處理方法的新認識。

1 風場數據介紹

本文以2008年7月實測獲得的臺風“海鷗”和“鳳凰”的風場數據進行分析，其中臺風“海鷗”于18日18時在福建長春鎮登錄，登陸時中心附近最大風力為10級（25m／s）；臺風“鳳凰”于28日22時在福建東瀚鎮登錄，登陸時中心附近最大風力為12級（33m／s）。兩次臺風過程的部分觀測數據相關說明見表1。

表1 觀測數據說明Table 1 Field measurement specifications

近地風場觀測點設置在溫州大學建工樓頂部，屬于城市市郊地形。在建工樓5層樓頂同一高度設置了兩臺WJ－3型風速風向儀，將其分別固定在9m高的直桿上（避免風速儀處風場受建工樓干擾）。兩風速儀離地總高度約為30m，水平相距約17m。采用DH－5937數據采集系統進行數據采集，采樣頻率為20Hz。

2 不同間隔滑動平均法

2.1 滑動平均法

在動態測試數據中，對確定性成分和不確定成分進行分離時，如若只要消除動態測試數據中的隨機起伏，而無需用某種函數或某些函數之和的形式來表示其變化規律，可采用平滑與濾波的數據處理方法，即滑動平均法來實現。該方法雖然是一種古典的數據處理方法，但在試驗數據處理中經常被采用。

假定動態測試數據y（t）由確定性成分f（t）和隨機性成分e（t）組成，且前者為所需的測量結果或有效信號，后者為隨機起伏的測試誤差或噪聲。經離散化采樣后，可相應地將動態測試數據寫成

為了精確地表示測量結果，抑制隨機誤差e（i）的影響，常對動態測試數據y（i）作平滑和濾波處理。如對非平穩的數據y（i），在適當的小區間上近似為平穩的，而作某種局部平均，以減小e（i）所造成的隨機起伏。這樣對沿全長N個數據以某一擬定的滑動間隔在逐一小區間上進行不斷的局部平均，即可得出較平滑的測量結果f（i），而濾掉頻繁起伏的隨機誤差［16］。其中，滑動間隔的大小對數據的處理結果有較大的影響。

2.2 基于滑動平均法的風場統計特征分析

眾多的研究者在進行風場特性分析時都采用10min離散平均的方式計算出相應的風場特性，即將風場數據根據時間序列按10min一段分成若干段（各段數據無重合），然后進行統計分析，以減小或消除測試誤差、噪聲以及短時距脈動的影響，得到風場的統計特征。但分析表明10min離散平均的統計分析結果不能很好的反映出強風風場的脈動性和變化規律，尤其是在實測風場數據較少的時候缺陷尤為明顯，如繪制出來的結果圖形數據點較少，不能連續地反映出風場的變化情況和脈動規律等。

因滑動平均法可有效地消除動態測試數據中的隨機起伏得到較為平滑的測量結果，是一種簡便而常用的數據處理方法。在此，為了解決10min離散平均進行風場特性統計分析的不足，本文提出采用滑動平均法對近地強風特性進行統計分析。如以10min為基本時距，將實測風場數據根據時間序列以某一時距為間隔進行滑動平均。如以1min間隔進行10min時距滑動平均時，截取的第一段數據即為0到10min之間的時間序列，第二段數據即為1min到11min之間的時間序列，依此類推。為了研究不同滑動間隔的影響，本文將以3s、10s、1min和10min為間隔進行滑動平均對比分析，其中以10min為間隔進行滑動平均實際上與10min離散平均方法相同。

3 近地面強風滑動平均統計特性對比分析

以下對實測獲得的臺風“海鷗”和“鳳凰”的風場數據，以3s、10s、1min和10min為間隔，進行近地面強風特性的10min滑動平均的對比分析，其中風場參數（如平均風速和風向角、湍流度、陣風因子和湍流積分尺度）的相關定義及計算公式詳見文獻［6－7］。限于篇幅，文中只給出了部分對比分析圖形和結果分析。

3.1 平均風速和風向角

圖1～圖3給出了臺風“海鷗”和“鳳凰”以3s、10s、1min和10min為滑動間隔的部分10min平均風速和風向角時程。結果表明，以3s、10s和1min為間隔的滑動平均對實測風場數據利用更加充分，如計算出的10min平均統計值更多，圖像連續性非常好，能較好地反映出平均速度、風向角隨時間的連續變化趨勢和短時段內的脈動規律，從而更加充分地揭示出近地強風平均風速和風向角的統計特性和脈動規律。相對而言，從10min滑動平均圖形很難獲得相應的規律。

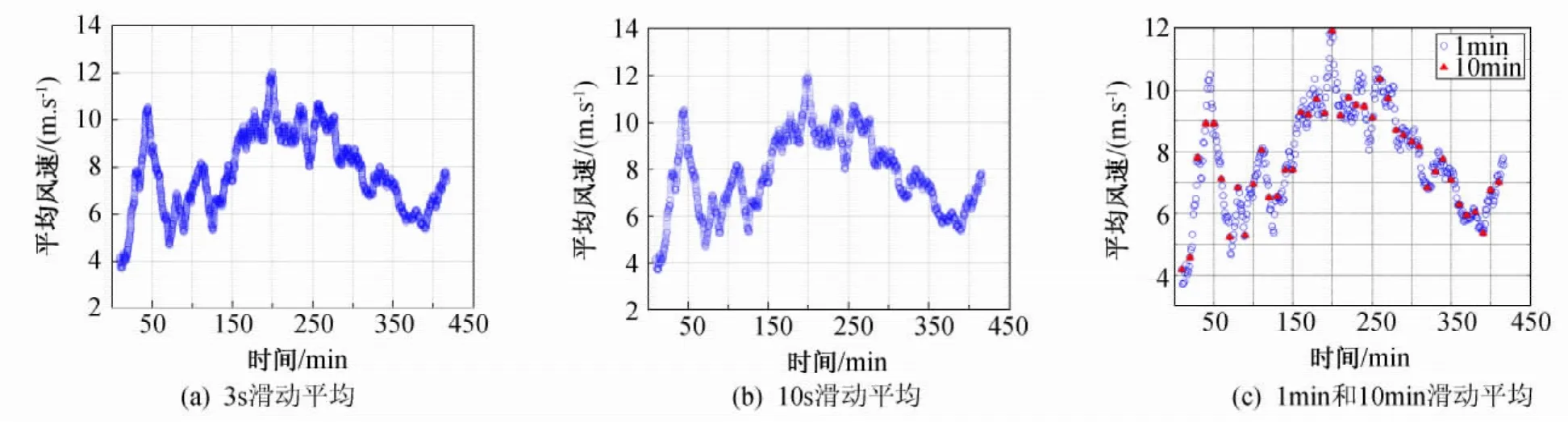
圖1 臺風“海鷗”的平均風速時程Fig.1 Mean wind speed time series of typhoon Kalmaegi

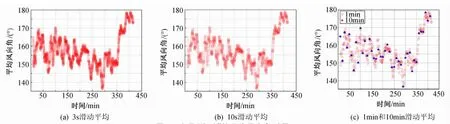
圖2 臺風“海鷗”的平均風向角時程Fig.2 Mean wind direction time series of typhoon Kalmaegi

圖3 臺風“鳳凰”的平均風速時程Fig.3 Mean wind speed time series of typhoon Fung－wong

另外，從圖1～圖3中可以看出，3s、10s滑動平均與1min滑動平均的連續性基本一致，都能很好的反映出10min平均風速、風向角隨時間的變化規律。因1min滑動平均的計算量要比3s、10s滑動平均的計算量小許多，所以在進行風場統計特性分析時采用1min滑動平均方法更加簡潔。

3.2 湍流度

湍流度反映了風的脈動強度，為確定結構所受脈動風荷載的關鍵參數。圖4～圖6給出了兩次臺風以10s、1min和10min為滑動間隔的部分10min時距的順風向和橫風向湍流度時程。由前述平均風速和風向角的對比分析可知，以3s滑動間隔計算得到的結果非常密集，此處及下文不再給出。圖4～圖6結果表明，10min滑動平均圖形中湍流度結果連續性差，很難反映出湍流度短時段內的變化趨勢及其脈動規律；以10s和1min滑動平均的湍流度脈動非常連續，且具有一定的周期性，較好地反映出了湍流度在不同時刻的變化趨勢和脈動規律，從而使研究人員獲得對風場湍流特性更加清晰的認識。

圖7給出了臺風“海鷗”以10s、1min和10min為滑動間隔的10min時距的順風向湍流度與平均風速的關系。圖7結果表明，10min滑動平均圖形中湍流度結果的數據點少、分布范圍小，其反映出的湍流度隨平均風速的變化趨勢和分布特征沒有10s和1min滑動平均結果好。尤其是在平均風速較大時因數據點太少，10min滑動平均結果基本不能反映出湍流度隨平均風速的變化規律。因強風的持續時間往往較短，而短時距滑動平均對實測風場數據利用更加充分，計算出的數據點多而密集，且其結果具有較好的連續性，從而能較好的揭示出風速較大時湍流度隨平均風速的變化規律。風速越大對建筑結構的作用也越大，所以風速較大時湍流度隨平均風速的變化規律往往對工程結構的抗風設計非常重要。

圖4 臺風“海鷗”的順風向湍流度時程Fig.4 Longitudinal turbulence intensity series of typhoon Kalmaegi

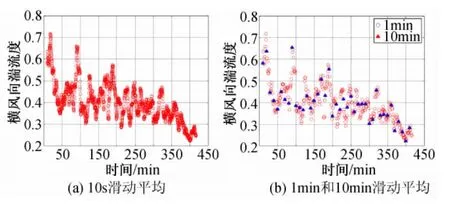
圖5 臺風“海鷗”的橫風向湍強度時程Fig.5 Lateral turbulence intensity series of typhoon Kalmaegi

圖6 臺風“鳳凰”的順風向湍流度時程Fig.6 Longitudinal turbulence intensity series of typhoon Fung－wong

圖7 臺風“海鷗”的順風向湍流度與10min平均風速的關系Fig.7 Relationship between longitudinal turbulence intensity and 10min mean wind speed during typhoon Kalmaegi

另外，圖4～圖7結果也表明，10s滑動平均與1min滑動平均的連續性基本一致，因1min滑動平均的計算量要比10s滑動平均小，所以在進行風場湍流度統計特性分析時1min滑動平均方法更加簡潔。

3.3 陣風因子

風的脈動強度也可用陣風因子來表示。圖8給出了臺風“海鷗”以10s、1min和10min為滑動間隔的10min時距的順風向陣風因子時程。總體看來，三種不同滑動平均的陣風因子的均值基本相同，但是三種不同滑動平均的最大值卻有較大差別。如臺風“海鷗”最大順風向陣風因子的10min滑動平均值分別比10s和1min滑動平均值小了18.4%和14.5%。另外，對比10s、1min和10min滑動平均的結果，也可以獲得與湍流度的不同間隔滑動平均統計特性對比中相似的結果。橫風向陣風因子的不同間隔滑動平均統計特性對比分析也能獲得相似的結果。

圖8 臺風“海鷗”的順風向陣風因子時程Fig.8 Longitudinal gust factor series of typhoon Kalmaegi

3.4 湍流積分尺度

湍流積分尺度是脈動風中湍流渦旋平均尺寸的量度，湍流積分尺度也是反映風場特性的一項重要指標。考慮到進行3s和10s滑動平均求解湍流積分尺度的計算量較大，圖9和圖10僅給出了臺風“海鷗”的1min和10min滑動平均的順風向與橫風向湍流積分尺度時程及其與平均風速之間的關系，其中湍流積分尺度根據Von Karman譜擬合實測風速譜得到［6］。圖9結果表明，相比10min滑動平均結果，1min滑動平均求得的湍流積分尺度的分布范圍更廣，圖像連續性較好，能較好地反映出湍流積分尺度隨時間的連續變化趨勢和短時段內的脈動規律。圖10結果表明，1min滑動平均求得的結果較密集，能較好地揭示出風速較大時湍流積分尺度與平均風速的關系及其變化規律。

圖9 臺風“海鷗”的湍流積分尺度時程Fig.9 Turbulence integral length scale series of typhoon Kalmaegi

3.5 湍流功率譜密度函數

脈動風速功率譜密度函數可以用來描述脈動風的特性，其在頻域上的分布可以描述湍流動能在不同尺度水平上的能量分布比例。基于前述風場特性的對比分析可知，基于不同時間間隔的滑動平均法對脈動風速功率譜進行對比分析時，也將獲得脈動風速功率譜沿著風場時程的連續變化規律以及在不同湍流度和風速情況下的特征，從而獲得對其新的認識。但基于不同時間間隔的滑動平均法對脈動風速功率譜進行對比分析時，需要非常多的結果圖形才能完成，所以文中沒有給出相關結果圖形的對比和分析。

4 結 論

基于2008年影響溫州地區的臺風“海鷗”和“鳳凰”的實測風場資料，以3s、10s、1min和10min為間隔，進行了近地面強風10min滑動平均統計特性的對比分析。研究結果表明，相對于以10min為間隔的滑動平均，以3s、10s和1min為間隔的滑動平均對實測風場數據利用更加充分，其結果具有更好的連續性，能較好地反映出平均速度、風向角、湍流度、陣風因子、湍流積分尺度和脈動風速功率譜密度函數隨時間的變化趨勢和短時段內的脈動規律，能較好的揭示出風速較大時湍流度、陣風因子、湍流積分尺度和脈動風速功率譜密度函數隨平均風速的變化規律，從而更加充分的揭示出近地強風的統計特性。3s、10s滑動平均與1min滑動平均的連續性基本一致，因1min滑動平均的計算量小，在進行風場統計特性分析時1min滑動平均方法更加簡潔。

［1］龐加斌，林志興，葛耀君.浦東地區近地強風風特性觀測研究［J］.流體力學試驗與測量.2002，16（3）：32－39.

［2］LI Q S，XIAO Y Q，FU J Y，et al.Full－scale measurements of wind effects on the Jin Mao Building［J］.Journal ofWindEngineeringandIndustrialAerodynamics，2007，95（6）：445－466.

［3］FU J Y，LI Q S，WU J R，et al.Field measurements of boundary layer wind characteristics and wind－induced responses of super－tall buildings［J］.JournalofWind EngineeringandIndustrialAerodynamics，2008，96（8／9）：1332－1358.

［4］陳麗，李秋勝，吳玖榮，等.中信廣場風場特性及風致結構振動的同步監測［J］.自然災害學報，2006，15（3）：169－174.

［5］戴益民，李正農，李秋勝，等.低矮房屋的風載特性：近地風剖面變化規律的研究［J］.土木工程學報，2009，42（3）：42－48.

［6］史文海，李正農，張傳雄.溫州地區近地強風特性實測研究［J］.建筑結構學報，2010，31（10）：34－40.

［7］史文海，李正農，張傳雄.溫州地區不同時距下近地臺風特性觀測研究［J］.空氣動力學學報，2011，29（2）：211－216.

［8］史文海，李正農，秦良忠，等.近地面與超高空臺風風場不同時距湍流特性對比分析［J］.建筑結構學報，2012，33（11）：18－26.

［9］史文海，李正農，羅疊峰，等.臺風“鲇魚”作用下廈門沿海某超高層建筑的風場和風壓特性實測研究［J］.建筑結構學報，2012，33（1）：1－9.

［10］郅倫海，李秋勝，胡非.城市地區近地強風特性實測研究［J］.湖南大學學報（自然科學版），2009，36（2）：8－12.

［11］李秋勝，戴益民，李正農，等.強臺風“黑格比”登陸過程中近地風場特性［J］.建筑結構學報，2010，31（4）：54－61.

［12］宋麗莉，吳戰平，秦鵬，等.復雜山地近地層強風特性分析［J］.氣象學報，2009，67（3）：452－460.

［13］黃世成，周嘉陵，王詠青，等.兩次臺風過程近地層湍流度和陣風因子分析［J］.氣象科學，2009，29（4）：454－460.

［14］申建紅，李春祥.強風作用下超高層建筑風場特性的實測研究［J］.振動與沖擊，2010，29（5）：62－68.

［15］陳凱，余永生，賈叢賢.傍山地區的強風場特性實測研究［J］.流體力學實驗與測量，2003，17（3）：18－22.

［16］裴益軒，郭民.滑動平均法的基本原理及應用［J］.火炮發射與控制學報，2001，1：21－23.