擺線槳氣動性能研究進展

唐繼偉，胡 峪，宋筆鋒

（西北工業大學 航空學院，陜西 西安 710072）

0 引 言

擺線槳是一種槳葉展向同旋轉軸軸向平行的推力裝置［1］（圖1a），通常由兩個以上槳葉組成，槳葉在繞擺線槳轉軸公轉的同時還繞鉸鏈作俯仰振蕩運動。懸停狀態時，槳葉的運動軌跡為圓周，而在前飛狀態下槳葉運動軌跡為擺線（圖1b），故名擺線槳［2］。

與旋翼和螺旋槳相同，擺線槳也是一種通過數個槳葉繞轉軸旋轉產生推力的旋轉翼推力裝置。不同之處在于：由于擺線槳槳葉在旋轉時展向與槳軸平行，槳葉展向的每個葉素都工作在相似的氣動條件下（如相似的流速、雷諾數和迎角），因此槳葉氣動力分布相對均勻，理論上槳葉能夠被優化到最佳氣動效率；由于槳葉周期性俯仰振蕩，槳葉產生的是非定常氣動力，槳葉動態失速過程可產生高升力；另外，由于擺線槳推力方向幾乎能在垂直于槳軸的任意方向進行瞬時調節，其相比傳統螺旋槳和旋翼系統，在提高飛行器（特別是微型飛行器）的機動性能方面具有很大優勢［1］。因此，將其作為未來垂直起降飛行器、高空長航時無人機、飛艇和艦船等諸多領域的推進系統［3］具有很好的應用前景。

擺線槳研究可以追溯到20世紀20年代［4］，美國海軍與華盛頓大學研究了擺線槳應用在飛艇上的可能性，但最終失敗。Wheatley等人［5－6］完成了早期擺線槳氣動力試驗，由于缺少對擺線槳設計參數的系統性研究，他們完成的這些實驗并沒有能夠證明其具備比旋翼、螺旋槳等升力和推進裝置更優越的氣動性能。二戰以后，隨著旋翼等裝置的廣泛應用，擺線槳研究一度中止。

20世紀90年代末，隨著材料和控制等相關學科發展，擺線槳重新引起了國外研究者的極大關注，美國海軍、Bosch Aerospace公司與密西西比州立大學［7－9］、馬里蘭大學［1，10－20］、韓國首爾大學［21－24］、日本筑波大學［25－27］和以色列宇航工程技術研 究中心（TITT）［28－29］等機構已在擺線槳研 究領域取得了一系列成果。在國內，西北工業大學近年開展了擺線槳相關研究工作［30－34］，研制了擺線槳飛行器原理樣機并成功實現了可控飛行［35］。

氣動性能是影響擺線槳應用前景的關鍵因素，對于擺線槳氣動性能及非定常流動機理的研究具有十分重要的理論意義和工程應用價值。目前，國外研究雖然已經取得了一些成果，但仍處于發展中，相關文獻并不多，還有許多關鍵問題亟待解決；而國內相關研究極少，有必要對其進展和現狀給予關注，綜合評估其應用潛力和發展方向。

本文介紹了擺線槳氣動力產生的基本原理和主要特點，從理論研究、數值模擬和實驗研究三個方面綜述了擺線槳氣動性能研究進展，對擺線槳氣動效率進行了探討，并對未來擺線槳氣動性能研究方向作出了展望。

1 推力產生原理及氣動力主要特點

1.1 推力產生及矢量推力原理

圖1為一個4槳葉擺線槳示意圖，圖1（a）為構成三維圖，其主要由槳葉（Blade），轉軸（Rotating shaft），支架（Support arm），推拉桿（Push rod）和偏心圓環（Eccentric ring）構成，圖1（b）為其中一個槳葉在擺線槳水平前飛狀態下時的運動軌跡。

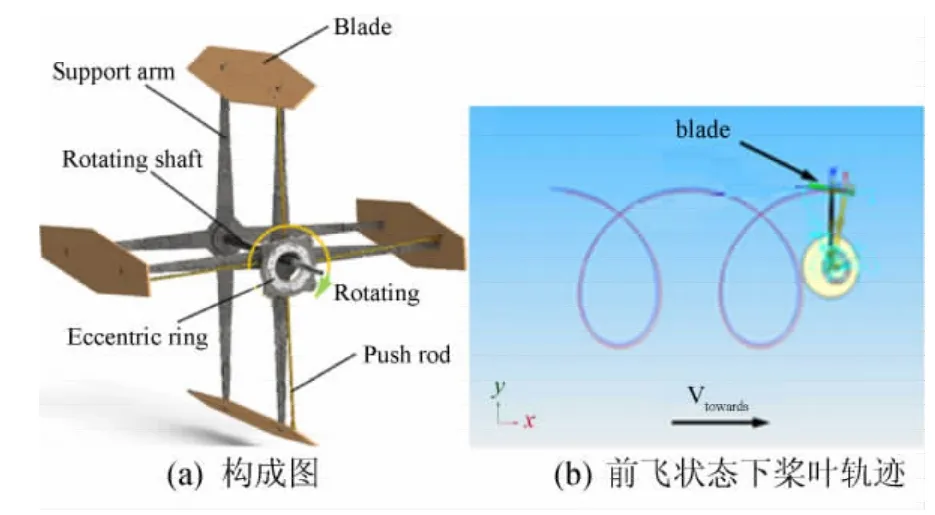
圖1 擺線槳示意圖Fig.1 The three－dimensional sketch map of cycloidal propeller and the orbit of a blade in forward flight

擺線槳產生氣動力的基本原理如圖2所示，圖中V為槳葉做圓周運動的切向速度，α為槳葉瞬時迎角。當偏心圓環（Eccentric ring）圓心（Offset point）相對擺線槳轉軸軸線（Axi centre）有一偏心距時，槳葉旋轉到上半周和下半周都是正迎角。轉動一周過程中，所有槳葉產生的瞬時升力、阻力投影到豎直方向和水平方向的力的平均值即為擺線槳的豎直推力和水平推力。通過控制機構改變偏心圓環的偏心距，可以改變槳葉的俯仰振幅，從而改變擺線槳的推力大小。

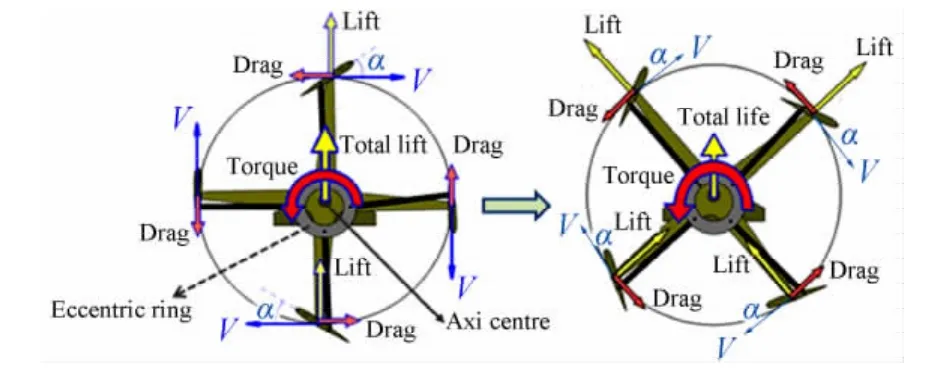
圖2 產生推力的基本原理Fig.2 The production principle of thrust

當擺線槳轉動過程中需要調節推力方向時，可通過控制機構拉動偏心圓環，改變其偏心角度（ε），從而改變槳葉瞬時迎角隨方位角的變化規律，產生垂直于轉軸的平面內360°任意方向上的推力，實現不同飛行狀態下推力方向的瞬時改變。圖3給出了改變擺線槳推力方向的原理示意圖。當偏心圓環圓心分別處于擺線槳軸線正下方（ε＝90°）、左下方（ε＝45°）、左側（ε＝0°）和左上側（ε＝－45°）時，其推力分別指向正上方，右上方，正右方和右下方。

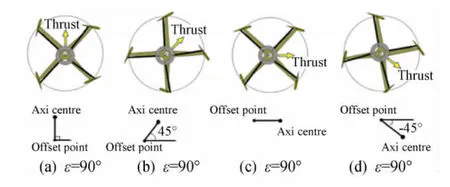
圖3 產生矢量推力原理Fig.3 The production principle of vector thrust

1.2 氣動力主要特點

1.2.1 槳葉俯仰振蕩產生非定常升力

擺線槳槳葉運動規律為繞圓周的周期性俯仰振蕩，槳葉剖面迎角按照近似正弦規律變化，這導致了很強的非定常流動狀態，可能出現動態失速現象，帶來如圖4所示的非定常動態升力，圖中CN為翼型俯仰振蕩時的法向力系數。因此，即使處于懸停狀態下的擺線槳，槳葉上的氣動力變化也是一個很復雜的動態過程，這使得定常和準定常的翼型氣動力理論模型已經不適合于擺線槳氣動力分析，需要采用合適的非定常流理論進行研究。

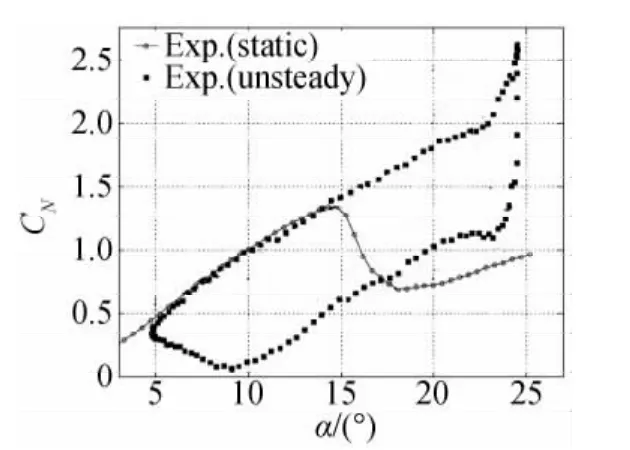
圖4 翼型非定常升力與靜態升力實驗值的比較［36］（馬赫數Ma：0.12，減縮頻率k：0.124，翼型NACA 0012）Fig.4 Comparison with experimental unsteady lift and steady lift（Ma＝0.12，k＝0.124，NACA 0012）

1.2.2 槳葉之間非定常干擾嚴重

擺線槳通常由2～6個槳葉組成，因此，槳葉非定常運動產生的尾流會對其他槳葉氣動性能產生很大的影響。這與螺旋槳槳葉干擾不同：無來流情況下，定距螺旋槳槳葉繞槳轂轉動時槳葉之間無相對運動，因而干擾幾乎是恒定的；而擺線槳每個槳葉都在作周期性振蕩運動，使得槳葉之間的干擾成為更加復雜的非定常干擾問題。

2 理論方法研究

理論方法具有快速高效的特點，在工程應用上具有重要意義。建立合理的擺線槳氣動力理論模型的關鍵在于如何更好地分析槳葉非定常氣動力和槳葉干擾等氣動力特點。目前，這方面的文獻還很少，下面按照求解槳葉非定常升力時是否考慮了流體粘性分別介紹：

2.1 基于無粘流假設的氣動力模型

Mcnabb［9］提出了基于薄翼振蕩理論［38］的擺線槳氣動力計算模型。該模型基于葉素理論計算槳葉的升力特性，假設流動為無粘流，采用翼型在定常流動條件下對應迎角時的零升阻力系數估算槳葉零升阻力，引入由實驗結果修正得到的經驗參數估算槳葉誘導阻力，并據此得到擺線槳的功耗（扭矩乘以轉速）。模型中采用入流效應分析各處下洗速度，基于均勻入流假設的單流管模型如圖5所示。圖中，Vt為入流速度，T為擺線槳拉力，D為擺線槳直徑。

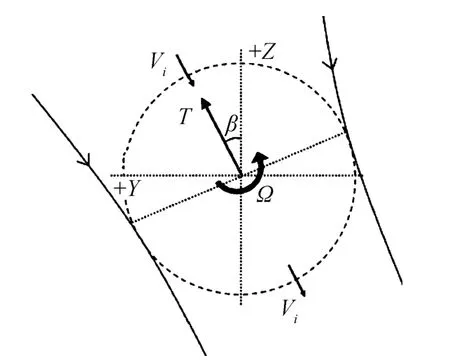
圖5 單流管模型示意圖［10］Fig.5 A diagrammatic sketch of single stream－tube

假設整個擺線槳完全浸處于一個流管中，入流速度Vi的大小在流管各處假設為恒定，其估算公式為：

式中，T為擺線槳推力，ρ為空氣密度，A為槳盤矩形投影面積（大小為擺線槳直徑乘以槳葉展長），Const為經實驗數據得到的槳盤面積修正系數。Vi的方向在迭代過程的每一周期中隨著合力方向而改變，槳葉運動到各處的來流速度為轉動引起的沿圓周切向速度疊加上Vi之矢量和。該模型計算結果與實驗值吻合較好，但文中的經驗參數是由他們的實驗數據修正得到的，這限制了其適用性。

Benedict［10］對基于流管模型的擺線槳氣動力分析方法進行了發展。該模型同樣假設流動無黏，基于薄翼理論得到翼型非定常升力和力矩的解析解。采用基于非均勻入流假設的多－雙流管模型，與采用單流管模型時的計算結果進行了對比，結果表明采用兩種流管模型得到的合力計算值均與實驗數據吻合較好，采用多－雙流管模型精度更高，而兩者對合力方向的計算精度均不夠高。該方法相對Maccnb模型的發展主要在于：計算過程未引入槳盤面積修正系數等經驗常數，更具一般性；多雙流管模型相比單流管模型更為細致地考慮了各處下洗速度，更加符合實際流場中的速度分布，因而可以提高計算精度。

胡峪［37］將非定常渦格法（UVLM）應用到求解擺線槳氣動力的計算中。非定常渦格法［38］的基本原理是假設流動無粘無旋，將槳葉表面劃分成多邊形網格，在各網格上布置渦環。求解時采用時間推進法，在第一個時間步，沒有尾渦存在，而僅有槳葉上的渦環。經歷一個時間步后，渦環從槳葉后緣不斷脫落，并以當地速度隨流體一起向下游運動。在運動過程中，各渦環強度需保持不變，以滿足理想流中的Kelvin環量守恒定理，并認為這樣就近似滿足了庫塔條件，且尾渦不受力。通過物面邊界條件，求解每一個時刻關于各渦環環量的線性方程組，再通過伯努利方程即可得到槳葉上的壓力分布和氣動載荷。圖6（a）是應用該方法得到的氣動力曲線，可以發現其雖具有一定精度，但與實驗數據仍有較大誤差；圖6（b）是槳葉尾跡的計算結果，可以看出，其并未得到槳葉尾跡由于下洗流影響向擺線槳下游流動的現象，這與實際觀察得到的情況不符［1］。

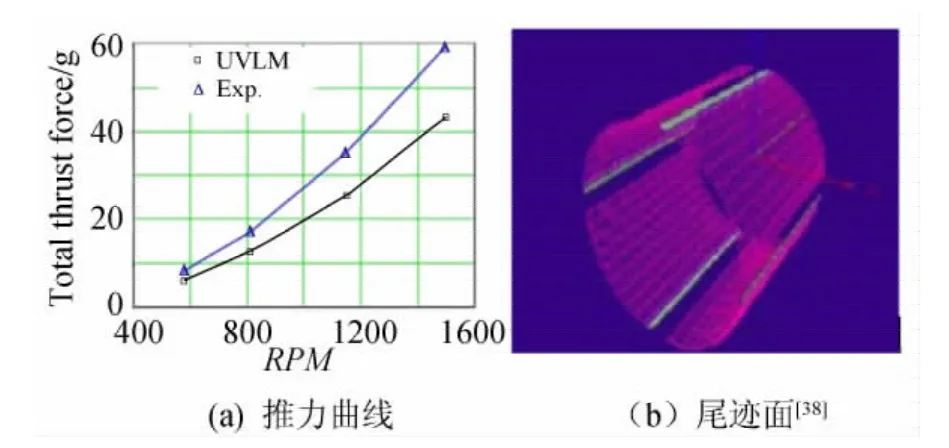
圖6 應用UVLM方法［38］求解的擺線槳推力和槳葉尾跡Fig.6 The thrust and wake structure of cycloidal propeller［38］

采用非定常渦格法對擺線槳氣動性能進行分析的優點是：考慮了槳葉間的氣動干擾；能對復雜槳葉外形進行分析，且計算量適中，具有一定精度。

以上三種擺線槳非定常氣動力理論模型的共同的局限是：都未考慮流體粘性，不能考慮具有分離流動和前緣分離渦的情況，因此只適用于減縮頻率低、槳葉迎角振蕩幅度小和未發生動態失速的流動情況，計算時經常出現較大誤差。

2.2 考慮流體粘性的氣動力模型

唐繼偉和胡峪［30－31］提出采用 Leishman－Beddoes（LB）動態失速模型的狀態空間法［39－40］來對擺線槳氣動性能進行分析。

該方法中采用的LB模型是研究翼型非定常氣動力的一種半理論半經驗模型［39］，給出了翼型出現前緣分離渦的判斷準則及其位置和離體渦長度如何確定的方法，可以很好的計算翼型俯仰振蕩非定常升力，在直升機旋翼和風力機設計中應用廣泛。LB狀態空間模型［40］在每一時刻需要求解含12個狀態量的一階微分方程組，包括8個從指數響應推導而來的線性附著流動狀態量，3個描述后緣分離產生的非線性氣動響應的狀態量，和一個用來判斷動態失速及流動重新附著的狀量。

采用該方法得到的計算結果與實驗數據吻合較好［30－31］。與 Maccnb和Benedict理論模型相比，采用LB模型的氣動力模型的改進主要是考慮了流體粘性，因而可以考慮具有后緣分離、前緣分離渦和動態失速的影響［30］。但由于采用單流管模型估算各處入流速度，因而不能對槳葉間的尾流干擾作細致分析；而基于葉素理論，不能很好地估算槳葉誘導阻力。

總的來說，目前尚還沒有一個精度高、應用廣泛的成熟擺線槳氣動力理論計算模型，需要發展無需引入經驗參數，并能計入考慮了流動粘性的槳葉非定常氣動力特性和槳葉干擾的理論計算方法。

3 數值模擬研究

計算流體力學的發展為擺線槳的非定常流場提供了一種有效的分析手段。近年來，國外研究者對擺線槳懸停狀態下的流場和氣動性能展開了為數不多的數值模擬研究：

首爾大學的Hwang等人應用Star－CD軟件的非定常計算模塊對擺線槳進行了數值模擬［22－24］，得到了其在懸停狀態下的流場和氣動力的周期性特征［24］，并利用數值模擬對擺線槳的氣動力進行計算，設計了一個安裝四個擺線槳的飛行器，實現了系留懸停［23］。為了模擬槳葉運動，采用滑移網格技術，將擺線槳全域（外圓域）作為轉動域，而每個槳葉周圍的小圓形子域作俯仰振蕩運動。他們對得到的數值模擬結果分析發現：下洗流穿過擺線槳內部時沒有彎曲；即使偏心方位角為零，擺線槳下游的出流偏離豎直方向也有10°～20°，如圖7所示，這與PIV實驗觀察到的定性一致；槳葉振蕩幅度一定時，其在圓周底部（ψ＝270°）時的合力比在頂部（ψ＝90°）時大，如圖8所示，他們認為這是弦線“彎度效應”造成的。

以色列的Gill Iosilevskii等人采用他們自己發展的計算程序EZNSS對擺線槳氣動性能進行了數值模擬［28－29］。該程序將流動假設為層流，采用非定常完全可壓縮N－S方程作為控制方程，采用非定常隱式時間推進。網格系統采用的是結構化嵌套網格，包括兩部分，隨擺線槳槳葉運動的CH型槳葉網格和笛卡爾背景網格。研究的擺線槳弦長1.5cm，展長15cm，槳盤直徑7.5cm，槳葉振幅15°～25°，轉速10000RPM，對應雷諾數為40000。通過對流線圖分析，他們發現擺線槳流場中兩側出現了較大的成對卷曲渦（Distorted Doublet），如圖9所示，這與有來流情況下的圓柱繞流產生的Magnus效應［41］類似。

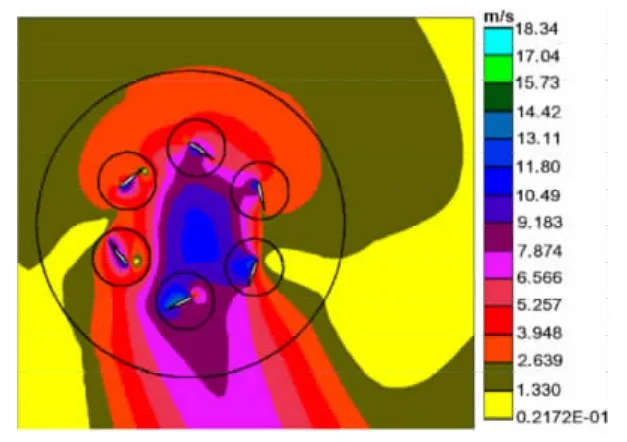
圖7 速度云圖Fig.7 The velocity magnitude contour

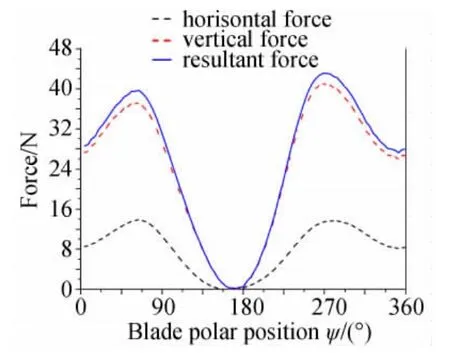
圖8 槳葉轉動一周的法向力、側向力與合力［24］Fig.8 Horizontal，vertical and resultant forces produced by a blade during one cycle of rotation［24］（CFD analysis）

圖9 瞬時流線圖［28－29］，10000RPM，Re＝40000Fig.9 Instantaneous streamlines［28－29］，10000RPM，Re＝40000

美國馬里蘭大學的Yang［20］通過基于結構化嵌套網格求解了預處理后的可壓縮非定常雷諾平均（RANS）方程，空間離散采用中心格式有限體積法，非定常隱式時間推進采用雙時間法。采用嵌套網格技術，將C－O型槳葉網格嵌套于圓柱形背景網格。在生成網格時，采用Benedict等人對擺線槳的結構動力學分析方法［18］考慮了槳葉展向的彎扭變形。對2槳葉擺線槳的氣動性能和流動特征進行了二維和三維數值模擬，得到的豎直方向的力與實驗數據吻合較好，但水平力和功耗與實驗值有較大誤差。

綜合來看，國外雖已經開始了一些擺線槳的數值模擬研究，但由于擺線槳繞流是極為復雜的低雷諾數強非定常流場，對于出現的漩渦等結構現有文獻中數值模擬的精度均不是很高；很少利用數值模擬方法對擺線槳力學特性進行深入分析，而國內對于擺線槳的數值模擬研究則剛剛起步，還需要大量的研究工作。

4 實驗研究

擺線槳設計參數主要包括：槳葉數、槳葉弦長、展弦比、槳葉實度、翼型、俯仰軸在弦向的位置和槳葉在上下半周的振蕩幅度等。由于擺線槳運行時槳葉所受到的離心力和振蕩帶來的慣性力較大，對單個槳葉的氣動力進行測量難度很大，因此，目前實驗中僅限于測量擺線槳總的推力和氣動功耗，且多為靜拉力實驗。通常采用動量理論分析擺線槳的懸停氣動性能，將其懸停效率FOM（figure of merit）定義為［1］：

其中，功率載荷PL為單位功耗產生的推力，即：

槳盤載荷DL為單位槳盤面積產生的推力，即：

氣動功耗：

以上各式中，T、A與公式（1）中定義相同，Ω為擺線槳氣動扭矩，ω為擺線槳轉動角速度。相同槳盤面積下，槳盤載荷相等時FOM大（即功率載荷大）的懸停效率高。擺線槳的前飛氣動效率定義與螺旋槳相同，定義為：

式中，Vtowards為擺線槳前飛速度。

美國海軍資助Bosch Aerospace公司與密西西比州立大學合作，研究擺線槳在飛艇上的應用前景［9］。他們設計了一個槳徑為1.22m、展長1.22m、弦長0.305m，NACA0012翼型的6葉擺線槳，并進行了一系列的靜拉力測試，以功率載荷（單位功率產生的拉力）為衡量指標，得到的結論是擺線槳的氣動性能比螺旋槳和涵道風扇好很多。但他們并沒有說明該比較是否在相同槳盤載荷下進行的。

首爾大學對擺線槳的槳徑、槳葉俯仰振蕩幅值、偏心方位角等參數進行了研究［24］，圖10是他們的實驗裝置。擺線槳展長0.8～1.0m，弦長0.15m，NACA0012翼型，轉速0～600RPM，槳葉振幅5°～30°，測試的槳葉數分別為2葉、3葉和6葉槳。他們發現：槳徑變大，槳盤面積增加，其氣動效率也越高，這與旋翼和螺旋槳相同；而槳葉振幅在一定范圍內變大時其氣動效率也在增加。在對槳葉數的影響進行實驗時發現，在相同槳盤載荷下，3葉槳比2葉槳的功率載荷高，而6葉槳最低。他們將1m槳徑擺線槳產生某一拉力時的功率載荷與旋翼的功率載荷相比，發現擺線槳的功率載荷更高。但同樣未指明是否在相同槳盤載荷作的比較。

圖10 首爾大學測力實驗裝置［24］Fig.10 Experimental setup in Seoul National University

日本筑波大學對三個槳葉的擺線槳［25－26］進行了實驗。擺線槳槳徑2m，展長1m，弦長0.3m，NACA0012翼型，測試轉速60～600RPM。他們發現擺線槳合力方向與豎直方向有約10°的偏角，這與Hwang［24］等人的數值模擬結果是定性一致的，且只有在槳葉迎角不斷改變過程中能觀察到，而在迎角不變（定距）的情況下無此現象［26］。

胡峪［2］在新加坡國立大學對小型擺線槳進行了實驗與分析。實驗中采用的擺線槳為3葉槳，槳徑140mm～270mm，展長140，梢跟比0.2～1.0，NACA0012和平板翼型，槳葉上半周（U）和下半周（D）振幅組合為 U45°D10°、U40°D35°、U20°D40°、U17.5°D45°、U5°D50°。他對實驗結果進行分析，發現在低雷諾數（1000～10000）下：薄翼型、矩形槳葉（展弦比為1）和上半周振蕩幅值小而下半周振蕩幅值大的設計可以使得擺線槳的效率較高。

以色列宇航工程技術中心［28－29］開展了擺線槳的相關氣動力實驗工作。擺線槳展長0.11m，弦長0.022m，直徑0.1116mm，屬于微小型擺線槳，如圖11所示，采用NACA0015翼型，振幅為0°～40°，轉速為4000RPM到6000RPM（相應的雷諾數為36000～50000）。實驗結果表明，安裝兩個槳葉的擺線槳在槳葉俯仰運動振幅為26°時開始失速；而4槳葉擺線槳在槳葉俯仰運動振幅為32°時開始失速。另外，擺線槳拉力偏轉方向可達10°～40°，且偏轉角隨著拉力增大而呈減小趨勢。

圖11 微小型擺線槳［29］Fig.11 Experimental micro－scale cycloidal propeller［29］

最近幾年，馬里蘭大學擺線槳研究團隊完成了大量擺線槳氣動力實驗，取得了一些重要成果［1，10－20］。實驗中采用的擺線槳槳徑和槳葉展長都約為0.15m左右，屬于微小型擺線槳，如圖12所示。他們對槳葉數、槳葉俯仰振幅、翼型、弦長、槳葉俯仰軸位置等對氣動性能的影響進行了研究。發現在相同槳盤載荷下：槳葉俯仰軸在弦向距前緣35%～45%弦長位置處效率最高；相同槳葉實度時，槳葉數越少效率越高；且槳葉振蕩幅度適當增大對提高擺線槳的氣動性能有利；而槳葉沿展向彎曲、扭轉變形和翼型彎度會對氣動性能帶來不利影響。另外，實驗中發現采用厚翼型和上半周振幅大、下半周振幅小時有利于提高氣動效率，這與胡峪［2］的實驗結論相反。

圖12 馬里蘭大學微小型擺線槳實驗［19－20］Fig.12 The experimental of micro－scale cycloidal propeller model in the University of Maryland［19－20］

馬里蘭大學擺線槳研究團隊的另外一個重要貢獻是：完成了擺線槳懸停狀態下的粒子成像（PIV）實驗［1，20］，揭示了一些重要的擺線槳流動現象和流場特征，主要為：觀察到槳葉會受到很強的下洗速度，圖13（a）所示得到的是不同尾跡壽命角（Wake age）時尾跡沿槳葉展向的無量綱速度分布，可以看到，尾跡平均速度可達60%～70%槳葉轉動速度［1］，使得槳葉的有效迎角大大減小，這解釋了為何槳葉振幅較大卻并未失速；圖13（b）是測得的槳葉附近渦量云圖，可以看到，槳葉上表面出現了前緣渦，這會帶來前緣吸力；另外，他們也觀察到了穿過擺線槳的尾流出現彎曲，解釋了擺線槳出現側向力的原因，指出這是擺線槳轉動帶來的 Magnus［41］效應；PIV實驗對于分析擺線槳的流動機理和驗證數值模擬的有效性具有重要意義。

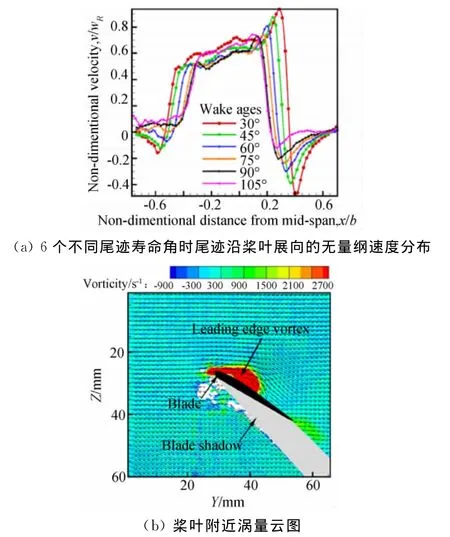
圖13 PIV實驗結果［1］Fig.13 The results of PIV experiment［1］

由于對擺線槳的關鍵設計參數對氣動性能的影響還不夠了解，馬里蘭大學早期微小型擺線槳靜拉力實驗得到的氣動性能數據并沒有微型旋翼等升力裝置好［10－14］。在最近的實驗［19］中，經過對設計參數 進行較為詳細的系統化實驗，找到了一個目前為止的最優微型擺線槳設計方案：4葉槳、NACA0015翼型、槳葉在上半周的最大振幅為45°、在下半周的最大振幅為25°，槳葉俯仰軸位于25%弦長處。采用對參數優化設計后的擺線槳模型進行靜拉力實驗，與相近槳盤面積的微型旋翼對比發現（圖14），在相同槳盤載荷時擺線槳的功率載荷比微型旋翼［17］高出很多。

5 擺線槳氣動效率探討

目前文獻中關于擺線槳與旋翼、螺旋槳等升力裝置或推進器相比，氣動效率高低的結論并不完全一致：某些文獻中，如文獻［7］認為擺線槳的氣動效率高，但他們所作的功率載荷對比圖并沒有說明是否在相同槳盤載荷下進行比較，因此結論不具有足夠的說服力；而某些實驗是在對擺線槳的設計參數對氣動性能影響不了解的情況下完成的，因此得到了擺線槳氣動性能不如旋翼等裝置的結論，這從馬里蘭大學近年來的微型擺線槳實驗研究歷程中可以看到［10－14］：隨著擺線槳研究的不斷深入，在對設計參數進行細致優化后，得到的相同槳盤載荷時微型擺線槳的功率載荷實驗數據要比微型旋翼高出很多［19］。由此可以看出，不同的擺線槳設計方案會大大影響擺線槳的氣動性能和效率高低，這也可能是不同研究者得到的實驗結論不一致的原因。然而，同螺旋槳、旋翼等技術的發展歷程一樣，這也是擺線槳研究必然經歷的過程。

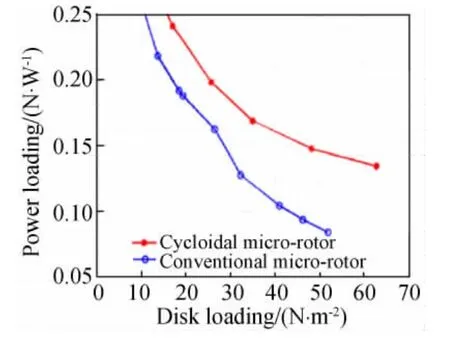
圖14 優化后的微型擺線槳與旋翼功率載荷對比圖［25］Fig.14 Power loading comparison between optimized micro－cycloidal propeller and micro－rotor［25］

綜合來看，從現有實驗數據分析，相同槳盤面積相同槳盤載荷時，擺線槳能夠具備比旋翼、螺旋槳等升力和推進裝置更高的功率載荷［19］，而若對擺線槳重要設計參數進行進一步優化，則其氣動效率還有可能進一步提高。

6 總結與展望

擺線槳是一種新型全向矢量推力裝置，近年來已成為國外航空領域研究熱點，引起了極大關注，國內外已研制出采用擺線槳作為升力、推力源的三軸（雙擺線槳垂直機身同軸轉動、一軸螺旋槳鎖尾）和四軸（四個擺線槳垂直機身呈雙排串列）等布局的垂直起降飛行器原理樣機，并初步實現了可控飛行，同時展開了將擺線槳作為飛艇等飛行器推進裝置的應用研究。總的來看，對擺線槳非定常空氣動力學特性的分析、流動機理的研究以及如何提高擺線槳氣動效率仍是目前擺線槳研究的技術難點。本文綜述了國內外擺線槳氣動性能研究進展，總結并展望如下：

（1）現有文獻中對擺線槳氣動效率高低的結論并非一致，但多認為擺線槳效率更高，且從最近馬里蘭大學的靜拉力實驗數據［19］來看，至少擺線槳懸停狀態下的氣動性能可優于旋翼等升力裝置，具備很高的工程應用潛力，值得國內研究人員關注。

（2）由于擺線槳的強非定常氣動特性，擺線槳空氣動力學理論仍不完善，目前的理論模型多存在著精度不夠高、適用性窄等不足。需要發展能夠考慮槳葉動態失速、槳葉誘導阻力和下洗干擾等因素的理論模型。

（3）擺線槳流動機理研究仍是難點，理論上，擺線槳可以利用俯仰振蕩帶來的非定常氣動效應延遲槳葉失速，從而產生高升力。但目前對擺線槳力的產生機制，特別是槳葉的氣動力特性進行闡述的文獻還很少；而擺線槳數值模擬仍在探索階段，未來有必要繼續完善，并結合PIV實驗等手段對其流動機理進行詳細解釋。

（4）從國內外的擺線槳實驗研究可以看到，目前完成的多是靜拉力實驗，對于前飛狀態下的擺線槳氣動特性了解還很少，未來需要進一步開展擺線槳相關風洞實驗；而傳統的螺旋槳相似理論不適用于擺線槳風洞實驗，需要首先建立擺線槳的相似準則，與螺旋槳相似理論類似，需要給出的主要是：擺線槳幾何相似、運動相似、動力相似、變形相似以及氣動性能公式相似準則，這是設計擺線槳縮比模型風洞實驗的理論基礎，但目前還沒有這方面研究工作的相關文獻可查，值得關注。

（5）文獻中關于擺線槳的一些設計參數如槳葉數、上下迎角幅值設計和翼型厚度等對氣動性能影響的結論尚不一致，需要進一步分析，特別是實驗驗證。通過對這些設計參數進行深入研究并優化，擺線槳的氣動效率還可能得到極大提高。

［1］BENEDICT M，RAMASAMY M，CHORPRA I，et al.Performance of acycloidal rotor concept for micro－air－vehicle applications［J］.JournaloftheAmericanHelicopterSociety，2010，55（2）：22202－1－22202－14.

［2］HU Y，LIM K B，HU W R.The research on the performance of cyclogyro［R］.AIAA－2006－7704，2006.

［3］SIEGEL S，SEIDEL J，COHEN K，et al.A cycloidal propeller using dynamic lift［R］.AIAA－2007－4232，2007.

［4］KIRSTEN F K.Cycloidal propulsion applied to aircraft［J］.TransactionsoftheAmericanSocietyofMechanicalEngineers，1928，50（AER－50－12）：25－48.

［5］WHEATLEY J B.Simplified aerodynamic analysis of the cyclogiro rotating－wing system［R］.United States：National Advisory Committee for Aeronautics，1933.

［6］WHEATLEY J B，WINDLER R.Wind－tunnel tests of a cyclogiro rotor［R］.United States：National Advisory Committee for Aeronautics，1935.

［7］GIBBENSR P.Construction and testing of a new aircraft cycloidal propeller［R］.AIAA－1999－3906，1999.

［8］BOSCHMAJ H.Modern aviation applications for cycloidal propulsion［R］.AIAA－2001－5267，2001.

［9］MCNABBM L.Development of a cycloidal propulsion computer model and comparison with experiment［D］.Mississippi，Mississippi State University，2001.

［10］SIROHI J，PARSONS E，CHOPRA I.Hover performance of a cycloidal rotor for a micro air vehicle［J］.Journal oftheAmericanHelicopterSociety，2007，52（3）：263－279.

［11］SIROHI J，PARSONS E，CHOPRA I.Cycloidal rotor micro air vehicle［C］.Proceedings of the 62ndAnnual Forum of the American Helicopter Society.Phoenix：Curran Associates，2006：18－31.

［12］BENEDICT M，SIROHI J，CHOPRA I.Design and testing of a cycloidal－Rotor MAV［C］.Proceedings of the International Specialists＇Meeting on Unmanned Rotorcraft.Chandler：Curran Associates，2007：404－410.

［13］BENEDICT M，CHOPRA I，RAMASAMY M，et al.Experimental investigation of the cycloidal－rotor concept for a hovering micro air vehicle［C］.Proceedings of the 64thAnnual Forum of the American Helicopter Society.Montreal：Curran Associates，2008：2571－2580.

［14］BENEDICT M，RAMASAMY M，CHOPRA I，et al.Experiments on theoptimization of the MAV－scale cycloidal rotor characteristics towards improving their aerodynamic performance［C］.Proceedings of the International Specialists′ Meeting on Unmanned Rotorcraft，Scottsdale：Curran Associates，2009：545－546.

［15］BENEDICT M，JARUGUMILLI T，CHOPRA I.Experimental performance optimization of a MAV－scale cycloidal rotor［C］.Proceedings of the AHS Specialists＇Meetings on Aerodynamics.San Francisco：Curran Associates，2010：20－22.

［16］BENEDICT M，JARUGUMILLI T，CHOPRA I.Design and development of a hover－capable cyclocopter MAV［C］.Proceedings of the 65thAnnual National Froum of the American Helicopter Society.Grapevine：Curran Associates，2009：27－29.

［17］HRISHIKESHAVAN V，CHOPRA I.Design and testing of a shrouded rotor MAV with anti－torque vanes［C］.Proceedings of the 64thAnnual National Froum of the American Helicopter Society.Montreal：Curran Associates，2008：28－30.

［18］BENEDICTM，CHOPRA I.Aeroelastic analysis of a MAV－scale cycloidal rotor［R］.AIAA－2010－2888，2010.

［19］JARUGUMILLI T，BENEDICT M，CHOPRA I.Experimental optimization and performance analysis of a MAV scale cycloidal rotor［R］.AIAA－2011－821，2011.

［20］KAN Yang，Aerodynamicsanalysis of an MAV－scale cycloidal rotor system using a structured overset RANS solver［D］.Maryland，University of Maryland，2010.

［21］HWANG I S，MIN S Y，LEE C H，et al.Development of afour－rotor cyclocopter［J］.JournalofAircraft，2008，45（6）：25－48.

［22］HWANG I S，MIN S Y，KIM M K，et al.Multidisciplinary optimal design of cyclocopter blade system［R］.AIAA－2005－2287，2005.

［23］HWANG I S，HWANG C S，MIN S Y，et al.Design and testing of VTOL UAV cyclocopter with 4rotors［C］.Proceedings of the 62nd Annual Forum of the A－merican Helicopter Society.Phoenix：Curran Associates，2006：1111－1117.

［24］KIM S J，YUN C Y，KIM D，et al.Design and performance tests of cycloidal propulsion systems［R］.AIAA－2003－1786，2003.

［25］NOZAKI H，SEKIGUCHI Y，MATSUUCHI K.Research and development on cycloidal propellers for airships［R］.AIAA－2009－2850，2009.

［26］MATSUUCHI K，OHTSUKA N，KIMURA Y.Cycloidal propeller and its application to advanced LTA to advanced LTA vehicles［R］.AIAA－2003－683，2003.

［27］NAKAIE Y，OHTA Y，HISHIDA K.Flow measurement around a cycloidal propeller［J］.TheVisualization SocietyofJapan，2010，13（4）：303－310，2010.

［28］IOSILEVSKII G，LEVY Y.Experimental and numerical study of cyclogiro aerodynamics［J］.AIAAJournal，2006，44（12）：2866－2870.

［29］IOSILEVSKII G，LEVY Y.Aerodynamics of the cyclogiro［R］.AIAA－2003－3473，2003.

［30］唐繼偉，胡峪，宋筆鋒等.基于LB動態失速模型的擺線槳氣動性能計算方法［J］，飛行力學，2011，29（3）：20－23.（TANG J W，HU Y，SONG B F，et al.Aerodynamics force computation method for cycloidal propeller basedon the LB dynamic stall model［J］.FlightDynamics，2011，29（3）：20－23.）

［31］HU Y，TANG J W，SONG B F.Aerodynamics analysis of cycloidal propeller［R］.ICAS 2012－2.7.1.

［32］胡峪，唐繼偉，宋筆鋒.一種安裝擺線槳的飛翼布局飛行器：中國，CN102556335A［P］：2012.07.11.（HU Y，TANG J W，SONG B F，et al.A cycloidal propeller flying wing aircraft：China，CN102556335A［P］：2012，07.11（in Chinese））

［33］胡峪，唐繼偉，宋筆鋒，等.一種擺線槳推進器：中國，CN102582830A［P］：2012，07.18.（HU Y，TANG J W，SONG B F，et al.A cycloidal propeller propulsion system：China，CN102582830A［P］：2012，07.18（in Chinese））

［34］胡峪，唐繼偉，宋筆鋒，等.一種擺線槳風扇：中國，CN102536862A［P］：2012，07.04.（HU Yu，TANG J W，SONG－B F，et al.A cycloidal propeller fan：China，CN102536862A［P］：2012.07.04（in Chinese））

［35］中國航空學會.首屆中航工業杯－國際無人飛行器創新大獎賽獲獎名單［J］.航空學會通訊，2011，10：10－11.（Chinese society of aeronautics and astronautics.Win－ning entries of the first AVIC cup－international UAV innovation grand prix［J］.ChineseSocietyofAeronautics＆Astronautics，2011，10：10－11.）

［36］SHENG W，GALBRAITH R A，COTON F N.Amodified dynamic stall model for low mach numbers［R］.AIAA－2007－626.

［37］HU Y，TAY W B，LIM K B.The analysis of cyclogyro using unsteady vortex lattice method［C］.Proceedings of 25thCongress of the International Council of the Aeronautical Sciences.Hamburg：Curran Associates，2006：930－935.

［38］KATZ J，PLOTKIN A.Low－speed aerodynamics［M］.Cambridge：Cambridge University Press，2001.

［39］LEISHMAN J G，BEDDOES T S.A semi－empirical model for dynamic stall［J］.JournaloftheAmerican HelicopterSociety，1989，34（3）：3－17.

［40］LEISHMAN J G，GILBERT L，CROUSE J.State－space model for unsteady airfoil behavior and dynamic stall［R］.AIAA 89－1389，1989.

［41］SEIFERTJ.A review of the magnus effect in aeronautics［J］.ProgressinAerospaceSciences，2012，55（3）：17－45.