連續流失效對近空間飛行器氣動特性的影響

黃 飛，張 亮，程曉麗，沈 清

（中國航天空氣動力技術研究院，北京 100074）

0 引 言

傳統航天飛行器在80km以上的高空大氣環境中高速飛行，其流動表現出稀薄效應，而對于未來采用升力體或乘波體構型［1］的近空間（20km～100km）高超聲速飛行器，由于其外形特征多為扁平狀升力面，具有尖化前緣、復雜氣動外形、長時間飛行和高升阻比等氣動構型和飛行軌道特征，飛行環境介于稠密大氣層和稀薄大氣層之間，其局部小尺寸部件在中等高空，甚至在較低的高空就會出現稀薄氣體效應。在稀薄流區，要實現飛行器的飛行、機動和控制，必須了解它們的氣動力特性，同時為飛行器防、隔熱設計提供氣動熱數據。而隨著飛行高度的變化，摩擦力、熱流等氣體動力學特性較之連續流區發生很大的變化。這些變化對于傳統的鈍頭體再入飛行器軌道影響較小，因此以往很少細致考慮稀薄氣體效應的影響，大余量的設計方法對于解決這類外型和軌道的飛行器已足夠，而對大升力面、尖化前緣復雜外形中低空飛行的稀薄流問題還有待研究。因此，中低Kn數的尖化前緣外形的氣動力、氣動熱的正確預測對近空間空域飛行器的設計和工程應用都具有重要意義。

在低空問題研究中，由于大氣密度高，常采用傳統的CFD方法進行流場的模擬分析，而飛行器飛行過程中，隨著飛行高度的變化，其所處的外部流動環境是一個漸變的過程，那么連續流假設在什么條件下失效？連續流計算方法對近空域飛行器氣動力、熱預測的偏差有多大？就成為目前急需解決的問題。國外已開展了許多關于連續流失效性判據［2－6］的研究工作，而對近空域稀薄效應對飛行器氣動特性變化的定量分析還不多見［7－9］。

本文首先采用了圓柱算例對四種滑移模型的有效性進行了對比分析，最后針對未來近空域飛行的高超聲速飛行器大升力面的構型特征，采用典型外形，選用適當的滑移模型和無滑移NS方法對近空間飛行器過渡流效應引起的氣動特性變化進行了對比分析，定量地給出了稀薄氣體效應對氣動特性的影響規律。

1 計算方法

1.1 N－S方程

在笛卡兒坐標系下，采用層流三維非定常可壓縮NS方程：

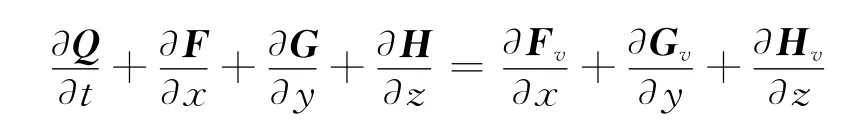
其中，Q為守恒變量；F、G、H為三個方向的無粘矢通量；Fv、Gv、Hv為三個方向的粘性矢通量。

1.2 滑移邊界類型

本文采用了四種滑移邊界模型，分別定義如下：Type1為經典的Maxwell滑移邊界類型；Type2為Gokcen［10］滑移邊界；Type3為 Lockerby［11］提出的壁函數修正法；HS為分子自由程采用硬球模型簡化計算時的Maxwell滑移邊界。

Type2（對應文獻［9］中CFD（2））：

Type3（對應文獻［9］中CFD（3））：

HS：

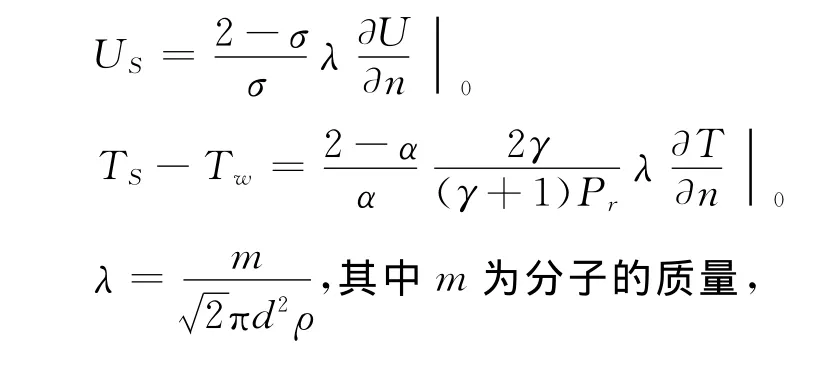
σ動量調節系數，α能量調節系數。

上述結果表明，在非高斯干擾明顯的環境中，原有算法性能會急劇下降甚至失效，但基于Alpha穩定分布的新算法可以有效完成雜波抑制，為接下來的動目標檢測奠定基礎。

1.3 無量綱參數定義

偏差分析量定義如下：

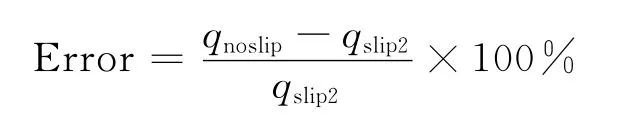
其中，qnoslip為無滑移NS方程熱流結果，qslip2為滑移模型Type2的熱流計算結果。

2 滑移模型的適應性分析

本文滑移模型的算例驗證采用文獻［9］中圓柱的計算條件，來流氣體為氬氣，來流馬赫數分別為Ma＝10、25，來流溫度T∞＝300K，圓柱直徑D＝304.8mm，基于直徑D＝2R的努森數Kn為0.002、0.05、0.25。本算例分別采用了 Type1、Type2、Type3、HS、No＿slip等方法對圓柱擾流進行了計算分析，并與文獻［9］中的DSMC結果進行了對比。此算例中的粘性系數計算方法見文獻［9］，對應于DSMC的VHS模型。

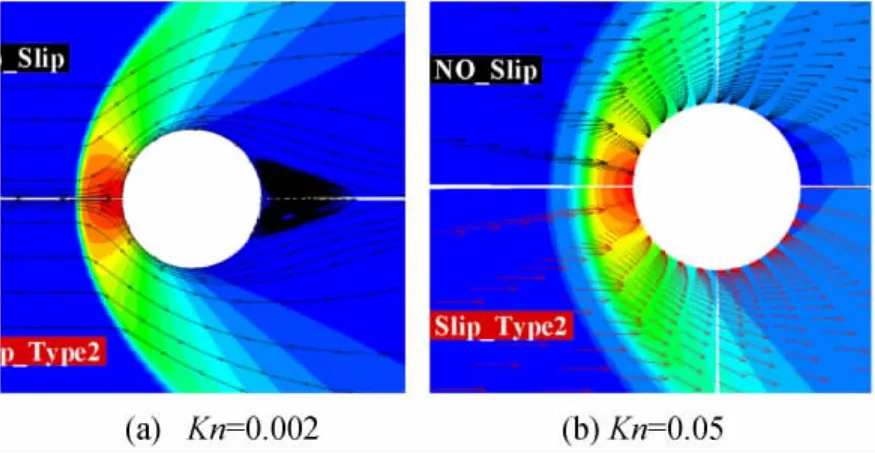
圖1 滑移與非滑移下Ar的流場結構（Ma＝10）Fig.1 Flow field with different methods（Ma＝10）

圖1（a）為Kn＝0.002時的流場壓力云圖，從中可以看出，滑移方法與非滑移方法在近連續流區所得到的流場結構非常一致，滑移流方法能夠準確捕捉激波結構和尾渦結構。圖1（b）為Kn＝0.05時兩種方法所得的流場壓力云圖和速度型，從圖中可以發現由于在此努森數下存在較弱的稀薄效應，兩種方法所得結果存在以下三點不同：滑移流方法所得的激波厚度比非滑移流方法稍厚；在物面處，滑移流方法所得的物面速度出現明顯的滑移速度，使得物面處速度型不同于非滑移流所得結果；在尾部區域，兩種方法所得的壓力等值線明顯存在不同。稀薄效應引起的以上三點不同將很有可能影響物面的熱流、壓力等分布。為了進行定量分析下面給出了不同滑移模型、非滑移方法、DSMC方法的物面氣動特性分布。

圖2分別給出了馬赫數等于10時，Kn＝0.002、0.05、0.25時不同滑移模型與DSMC方法所得的熱流系數分布曲線，其中圖2（a）為本文計算結果，圖2（b）為文獻［9］計算結果。從圖中可以看出，在較弱稀薄效應下，即努森數Kn＝0.002時，不同滑移模型所得熱流系數分布與DSMC結果吻合較好，當努森數Kn增加到0.05、0.25時不同模型所得結果之間的差距開始明顯顯現；隨著努森數的增加，無滑移NS方法所得熱流分布都一致的高于滑移方法及DSMC方法所得結果，并且從圖中可以發現，類型2的滑移模型即使在較大努森數Kn＝0.05、0.25時也表現出了與DSMC相一致的結果，其它模型所得結果在較大努森數下都一致高于DSMC方法所得結果，由此可見，類型2的滑移模型對較大努森數下具有更好的適應性，其它模型的結果都將高估熱流而使得防熱設計趨于保守。通過與文獻結果對比可以發現，本文與文獻結果熱流分布吻合很好。

圖3分別給出了Kn＝0.002、0.05、0.25時本文與文獻［9］采用不同滑移模型與DSMC方法所得的壓力系數分布曲線，從圖中可以看出，當努森數Kn＝0.002、0.05時，不同滑移模型所得表面壓力系數分布與DSMC所得結果非常一致，當努森數增加至0.25時，各種模型所得壓力分布都一致高于DSMC方法所得結果，這主要是因為強烈的稀薄效應使得NS方法所得激波結構明顯薄于DSMC方法所得激波結構，NS方法產生的激波壓縮性更強，使得波后壓力較高。從圖2熱流系數分布和圖3壓力系數分布對比結果可以看出，相對于熱流而言，壓力對稀薄效應敏感性較弱。通過與文獻結果對比可以發現，本文與文獻結果壓力分布同樣吻合很好。

圖4、圖5分別給出了馬赫數等于25時，Kn＝0.002、0.05、0.25時本文采用不同滑移模型所得的熱流系數與壓力系數分布曲線與文獻［9］DSMC方法的結果比較，從圖中可以看出，馬赫數等于25時的熱流、壓力分布規律與馬赫數等于10時的分布規律不同之處僅在于量值上的不同，其它規律與馬赫數等于10時的結果相似，類型2的滑移模型在較大馬赫數下也同樣具有較好的適應性。

綜合以上計算分析可以得出以下結論：通過本文計算結果與文獻［9］所得結果的對比可以發現，本文結果與文獻結果吻合較好，本文所發展的代碼具有一定的可靠性；滑移模型2的適應范圍較其它模型更廣，它能夠在較大努森數下取得相對較為滿意的熱流結果；在較大努森數下，滑移模型所得熱流、壓力結果都一致高于DSMC結果，使得防熱設計趨于保守；相對于熱流而言，壓力對稀薄效應的敏感性更弱；經過數值模擬還可以發現，模型2雖然適應性廣，但相對于其它模型而言，計算時較為耗時，收斂性較差，對網格要求較高，如果在飛行器防熱設計條件允許下，可以考慮采用其它幾種滑移模型。

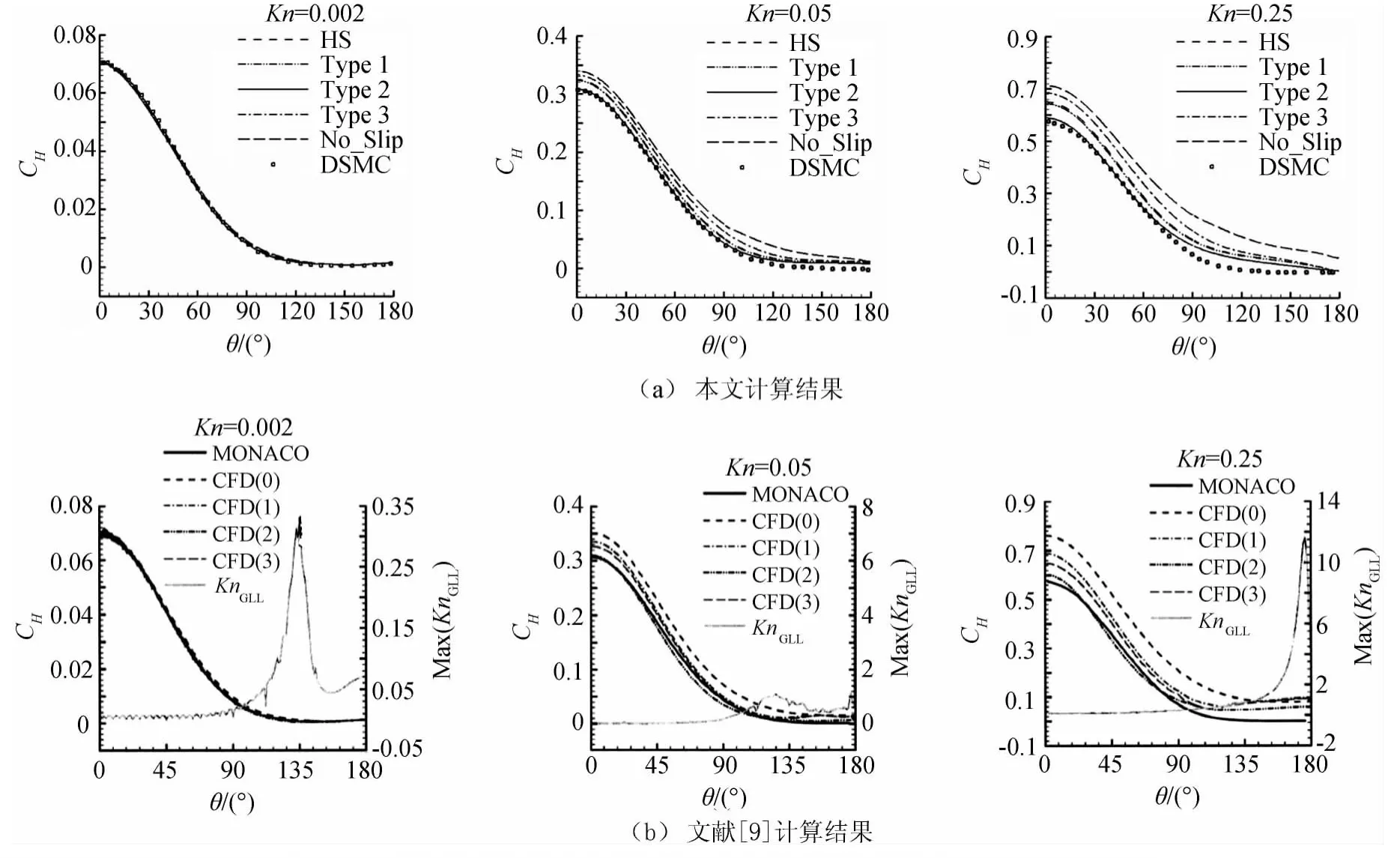
圖2 不同滑移模型在不同努森數下的物面熱流系數分布（Ma＝10）Fig.2 Heat transfer rate on the surface at different Knnumbers（Ma＝10）

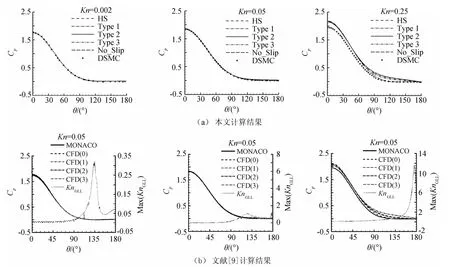
圖3 不同滑移模型在不同努森數下的物面壓力系數分布（Ma＝10）Fig.3 Pressure coefficient on the surface at different Knnumbers（Ma＝10）

圖4 不同滑移模型在不同努森數下的物面熱流系數分布Fig.4 Heat transfer rate on the surface at different Knnumbers（Ma＝25）

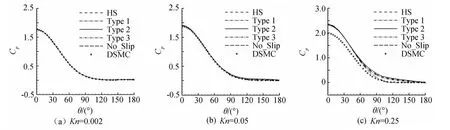
圖5 不同滑移模型在不同努森數下的物面壓力系數分布Fig.5 Pressure coefficient on the surface at different Knnumbers（Ma＝25）

3 梯形翼近空間氣動特性的計算分析

由于滑移模型2在稀薄氣動特性預測方面的適應范圍更廣，預測結果更為接近DSMC結果，故本文針對馬赫數15，飛行高度h＝50km～80km的梯形翼主要采用了模型2進行了稀薄氣動特性的計算分析。飛行攻角為10°，壁溫為500K，翼前緣直徑為30mm，翼根弦長約1.96m，翼尖弦長約0.63m，翼展長為0.5m，前緣后掠角約20°。

圖6為本文所采用的計算網格示意圖，圖7給出了梯形翼不同位置處的截面示意圖，其中Z＝5mm為梯形翼對稱面部位，Z＝300mm為翼中部位。為了進行定量分析，以下給出了截面位置處不同方法所得結果的差異性比較分析。

圖8、圖9分別為攻角10°下截面Z＝5mm、Z＝300mm處不同方法所得的表面熱流分布及偏差曲線結果，從上圖熱流分布結果可以發現，在相對較低的飛行高度，滑移方法與無滑移方法所得結果較為一致，隨著飛行高度的增加，兩種方法所得結果的差距逐漸增大。從圖9偏差曲線圖的定量結果可以明顯看出，由于迎風面氣體壓縮，背風面氣體膨脹，使得滑移的影響首先出現在背風面，故無滑移方法與滑移方法之間的差距在迎風面明顯低于背風面，并且隨著飛行高度的增加，稀薄效應越明顯，滑移方法與非滑移方法所得的熱流結果之間的偏差逐漸增大。從圖中還可發現，此偏差最大值主要發生在翼前緣背風面膨脹區附近，當此種飛行器從50km至80km飛行時，在飛行器翼面大面積上的偏差約在5%至15%之間變化。

表1為不同高度下滑移方法和無滑移方法所得氣動力特性的結果比較，從中可以看出，隨著飛行高度的增加摩阻系數、軸向力系數、法向力系數都有所增加，其中摩阻增加較大，故而可以發現，升阻比隨著高度的增加逐漸減小。從不同方法的偏差結果可以看出，隨著飛行高度的增加，氣體稀薄度增加，稀薄效應增強，傳統無滑移假設下的NS方法已不能正確描述壁面邊界條件，故而兩種方法所得結果的偏差量逐漸增大。

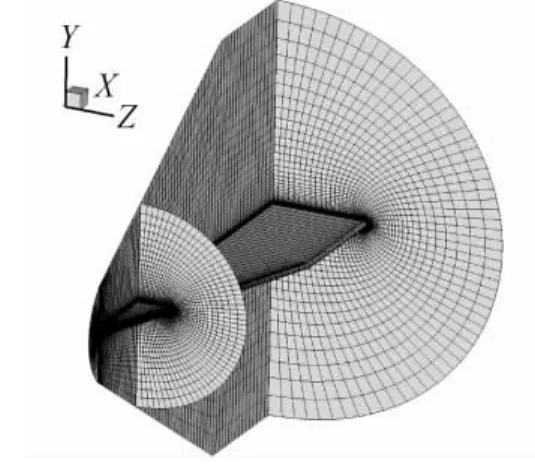
圖6 計算網格示意圖Fig.6 Grid in the computation region

圖7 不同位置處的截面示意圖Fig.7 Slice at different stations

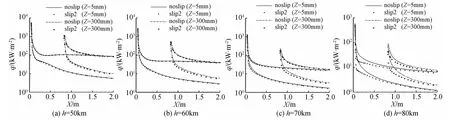
圖8 不同位置處的熱流分布結果Fig.8 Heat flux at different stations

圖9 偏差分析結果Fig.9 Error at different stations

表2為不同方法所得峰值熱流隨高度的變化，從中可明顯看出，隨著高度的增加，氣體密度降低，飛行器前緣的峰值熱流降低較快，而采用滑移與無滑移兩種方法所得的結果偏差則隨著高度的增加而增大，這主要是由于高度的增加使得稀薄度增大，傳統連續流假設下的無滑移方法不再有效。

表1 不同方法下的氣動力特性結果Table 1 Aerodynamics with different methods

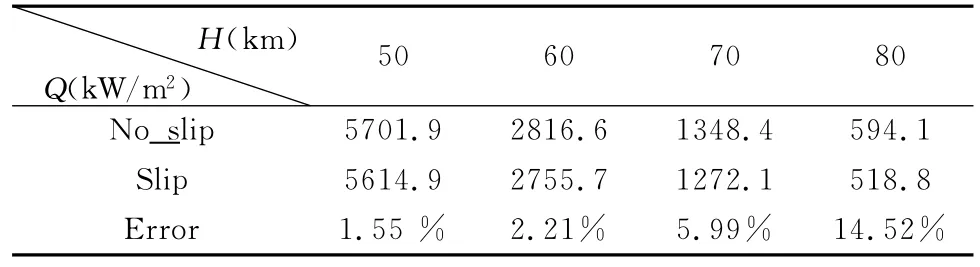
表2 不同方法下的峰值熱流結果Table 2 Peak heat flux with different methods

4 結 論

高超聲速飛行器飛行過程中經歷了不同大氣環境密度的變化，本文針對中低空域大升力面飛行的高超聲速飛行器的結構特征，采用典型外形研究了連續流失效后不同滑移模型對表面氣動特性的預測能力，最后給出了大升力面梯形翼近空間氣動特性的變化規律。結果表明：

（1）本文所得規律與文獻結果吻合很好，所建立的模擬手段具有一定的可靠性。

（2）滑移模型2比其它模型適應范圍更廣，能夠在較大努森數下取得相對較為滿意的結果。

（3）在較大努森數下，除了滑移模型2以外，其它模型所得熱流、壓力結果都一致高于DSMC結果，使得防熱設計趨于保守。

（4）相對于熱流而言，壓力對稀薄效應的敏感性較弱。

（5）在本文所研究的尺寸下，當大升力面梯形翼的飛行高度從50km增加至80km時，滑移方法與無滑移方法在翼面大面積上所得的熱流偏差量約在5%至15%之間變化；而駐點處峰值熱流的偏差量約在1.6%至14.5%之間變化；相應的升阻比偏差結果約在0.06%至14.38%之間變化。

［1］李怡勇，沈懷榮.發展近空間飛行器系統的關鍵技術［J］.裝備指揮技術學院學報，2006，17（5）.

［2］BIRD G A.Breakdown of translational and rotational equilibrium in gaseous expansions［J］.AIAAJournal，1970，8（11）：1998－2003.

［3］TIWARI S.Coupling of the boltzmann and Euler equations with automatic domain decomposition［J］.Journal ofComputationalPhysics，1998，144：710－726.

［4］CAMBEROS J A，SCHROCK C R，McMULLAN R J.Development of continuum onset criteria with direct simulation Monte－Carlo using boltzmann＇s H－theorem：review and vision［R］.Proceedings of the 9th AIAA／ASME Joint Thermophysics and Heat Transfer Conference，San Francisco，California，June 2006.

［5］BOYD I D，CHEN G，XANDLER G V.Predicting failure of the continuum fluid equations in transitional hypersonic flows［J］.PhysicsofFluids，1995，7（1）：210－219.

［6］WANG W L.A hybrid particle／continuum approach for nonequilibrium hypersonic flows［D］.［Ph.D.Thesis］.The University of Michigan，2004.

［7］BOYD I D，PADILLA J F.Simulation of sharp leading edge aerothermodynamics［R］.AIAA Paper 2003－7062.

［8］LOFTHOUSE A J，BOYD I D，etc.Effects of continuum breakdown on hypersonic aerothermodynamics［R］.AIAA Paper 2006－993，2006

［9］lOFTHOUSE A J，SCALABRIN L C，BOYD I D.Velocity slip and temperature jump in hypersonic aerothermodynamics［R］.AIAA Paper 2007－0208，2007.

［10］GOKCEN T，MACCORMACH R W.Nonequilibrium effects for hypersonic transitional flows using continuum approach［R］.AIAA Paper 1989－0461，1989.

［11］LOCKERBY D A，REESE J M，GALLIS M A.Capturing the knudsen layer in continuum－fluid models of nonequilibrium gas flows［J］.AIAAJournal，2005，43（6）：1391－1393.