基于提升小波變換的圖像去噪方法研究
張亞飛 馮小華
(中南大學 信息科學與工程學院,湖南 長沙 410012)
圖像去噪問題一直都是圖像處理領域的研究重點, 噪聲的干擾往往會嚴重影響圖像的質量,給后續的圖像分析及應用帶來極大的不便,為此研究者們一直在尋求一種既能有效地減小噪聲,又能很好地保留圖像重要特征的去噪方法。 與傳統的小波變換去噪方法相比, 提升小波變換以其獨特的算法結構,降低了計算復雜度, 易實現整數到整數的變換等特點,成為小波研究與應用領域新的熱點。
1 小波變換
小波分析是一種信號的時頻分析方法,它具有實時、多分辨率、自適應等特點,在時頻兩域都具有很強的表征信號局部特征的能力,因而在圖像去噪領域中得到了廣泛的應用。
小波一詞由Morlet 和Grossman 在1980 年代早期提出。傳統的小波通常是由定義在L2(R)空間上的容許函數ψ(t)經過伸縮、平移變換生成的,這種小波通常被稱為第一代小波,其基本定義如下:
如果ψ(t)是一滿足條件的基小波或母小波,將其經過伸縮和平移變換后,就可得到一簇函數,形式如下

此函數被稱之為小波函數簇, 其中a 為伸縮因子,b 為平移因子。 進而定義下式
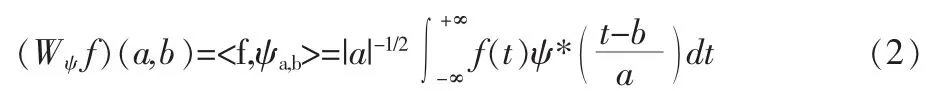
為關于基小波ψ 的連續小波變換。 其中,ψ*(t)表示對ψ(t)的共軛運算。
2 提升小波變換
通過以上分析, 傳統的第一代小波變換是在歐氏空間內通過基底的平移和伸縮來構建小波基的,這種變換雖然克服了傅立葉變換所存在的固定分辨率、難以同時兼具時頻分解特性等問題,但其本身也存在著算法復雜度高、占用內存大、浮點運算誤差大、不利于硬件實現等缺點。 為此,1995 年Sweldens 提出了一種不依賴于傅里葉變換的新的小波構造方法—提升方法,稱為第二代小波變換。
第二代小波提升算法基本思想是通過一個預測算子,確定高頻信息,并初步確定低頻信息;然后通過更新算子,對初步確定的低頻進行修正,從而確定低頻信息。 基于提升方案的第二代小波變換過程可分為三個階段:分解(Split)、預測(Predict)和更新(Update)。
(1)分解:將輸入信號sj分為2 個較小的子集sj-1和dj-1。最簡單的辦法是將輸入信號sj根據奇偶性分為2 組,這種分解方法所產生的小波也稱為“懶小波”,數學表達式描述如下:

(2)預測:在基于原數據相關性的基礎上,用偶數序列sj-1的預測值P(sj-1)去預測奇數序列dj-1,然后用dj-1與預測值P(sj-1)的差來替換dj-1。 用數學公式描述如下

式中為預測算子, 一般可以通過差值細分方法構造。 這樣,產生的dj-1比原來的dj-1包含更少的信息,繼續用更小的子集sj-1和dj-1來代替原來的信號集sj, 重復分解和預測過程,最終原始信號集可以用{sn,dn,……,s1,d1}來表示。
(3)更新:更新的思想主要是要構造一個算子U,利用小波子集dj-1對sj-1進行更新, 從而使sj-1繼續保持原來數據序列的某些特征。 數學公式描述如下

此外,小波提升變換過程是可逆的,只需改變式(3)(4)(5)的計算次序和符號就可以得到重構的數據序列。
3 實例分析
在Matlab(R2010b)環境下,以woman 為原始圖像進行仿真實驗,分別利用傳統小波變換和本文所介紹的提升小波變換對含噪圖像進行處理,仿真結果如圖1 所示。

圖1 提升小波變換圖像去噪效果圖
4 結論
仿真實驗結果可見, 基于提升小波變換的圖像去噪效果與傳統小波變換相當, 但考慮到提升小波變換運算復雜度低、實現過程簡單快速等優點,以較小的代價實現了預期的處理效果, 這無疑驗證了基于提升小波變換的圖像去噪方法的優越性。 同時,針對提升小波變換的實現過程,我們可以看到數學理論方法的改進對于提高運算效率的重要性,可以預見在小波分析領域,根據實際情況合理選擇先進的數學變換方法,對于實現問題最優化解的重要意義。
[1]張德豐,等.MATLAB 小波分析[M].北京:機械工業出版社,2011
[2]趙慶光.基于提升小波變換的圖像去噪算法研究[D].哈爾濱:哈爾濱工業大學,2009
[3]林祥云.基于提升小波變換的圖像去噪[D].武漢:武漢紡織大學,2010

