蓄能器平衡回路對主軸直線運動的影響
李曉會
(北京工研精機股份有限公司,北京 101312)
目前基于節能降耗的思想,越來越多的數控機床廠家采用蓄能器平衡主軸重量;然而實際應用中,許多設計人員對此平衡回路各參數的選擇與設定不甚了解,造成機床精度較低,或延長調試周期。本文通過對其數學模型的分析,給出各參數選擇與設定的參考依據及建議。
1 蓄能器平衡回路數學模型及其分析
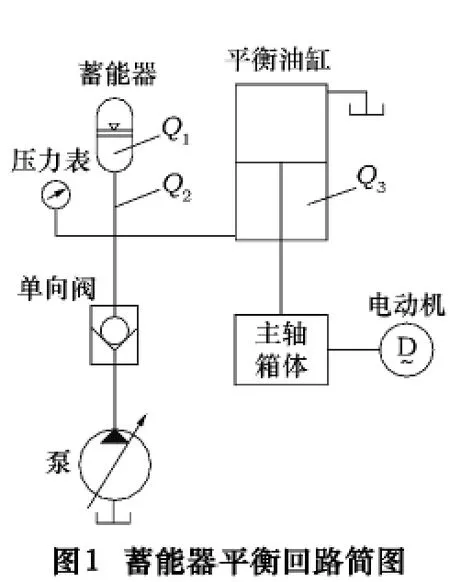
在某臥式機床的液壓控制回路中,Y軸中有關蓄能器平衡主軸箱重量部分的典型回路簡圖如圖1。
此回路的工作原理是:從泵經單向閥向預先充有一定壓強的氮氣的皮囊式蓄能器充油,當蓄能器內壓強達到設定值時,泵停止工作。當Y軸電動機帶動主軸箱上下運動時,驅使與之硬連接的平衡油缸活塞聯動,油缸內下腔油容積的變化引起蓄能器內油液體積的變化,從而引起氣囊內氮氣壓強的變化;而這種壓強又通過油液反作用回油缸內,所以主軸箱被平衡的重量在Y軸運動過程中不斷變化。
通過對上述回路建立數學模型,得出主軸箱無論是下行或上行,蓄能器平衡回路的傳遞函數G(s)為
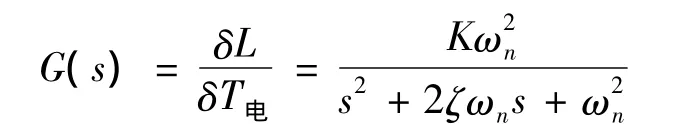
式中:δL為主軸箱位移的變化量;δT電為電動機輸出扭矩的變化量;K為回路增益;ωn為固有頻率;ζ為阻尼比。
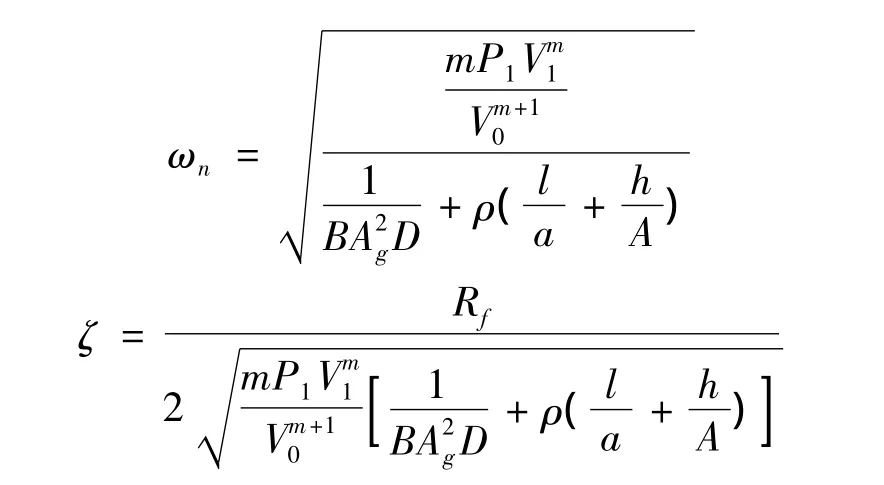
其中:P1為蓄能器的充氣壓強;V1為蓄能器的容積;V0為平衡點時蓄能器的容積;m為氣體常數;ρ為油液密度;l為從蓄能器至平衡油缸之間的連接管路長度;a為連接管路的通流面積;Rf為管路液阻;h為蓄能器內液體高度;A為蓄能器中油液的截面積;Ag為平衡油缸有效作用面積;B,D為與機械結構有關的常數。
從上式可得出回路有以下特點:
(1)穩定性 根據勞斯判據知此系統是漸近穩定的。(2)固有頻率 當蓄能器的充氣壓強、工作壓強越大時,系統固有頻率越高;當蓄能器內和連接管路中油液的質量M越小時,系統固有頻率越高,即減小管路長度、蓄能器高度,或增大管路面積、蓄能器面積,將會提高固有頻率。(3)阻尼比 當蓄能器的充氣壓強、工作壓強越大,系統阻尼比越小。
2 實驗驗證
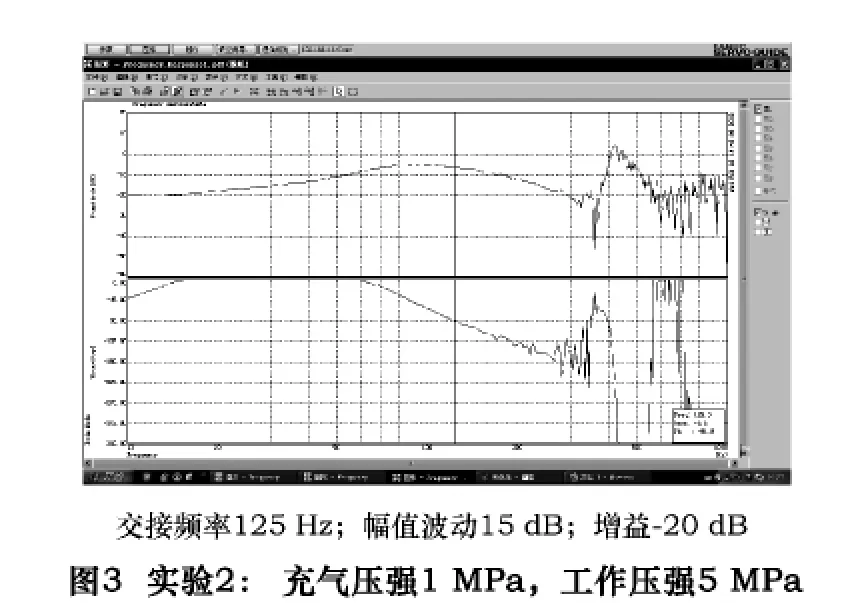
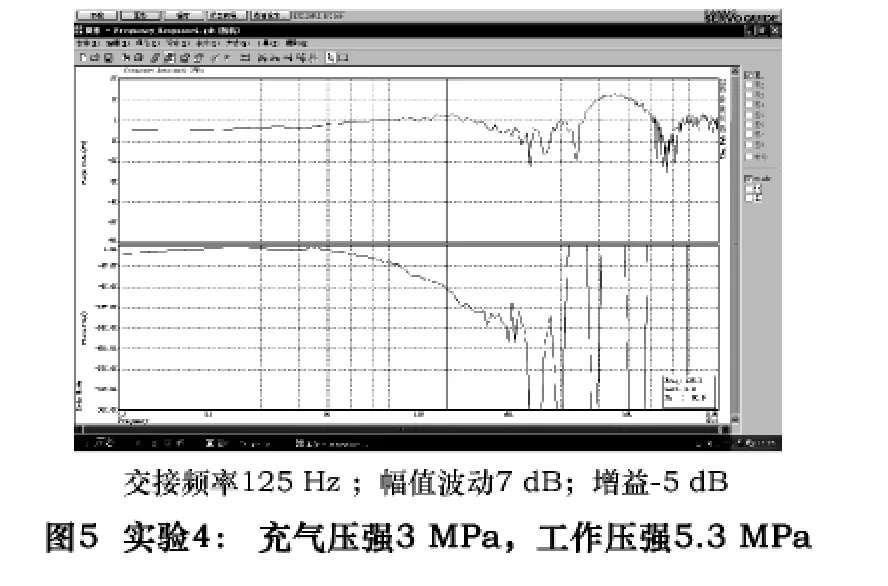
為了驗證平衡回路中各參數對伺服傳動系統的影響,筆者對某臥式數控機床的Y軸作了一些實驗,實驗結果見圖2~5。實驗1、實驗2、實驗3分別是在同樣蓄能器、同樣的充氣壓強下,改變回路中油液多少的條件下進行的;實驗4是在同樣的蓄能器、不同的充氣壓強下進行的。
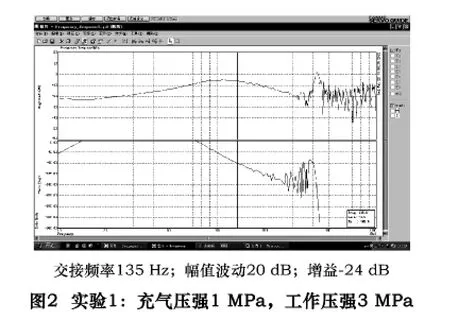
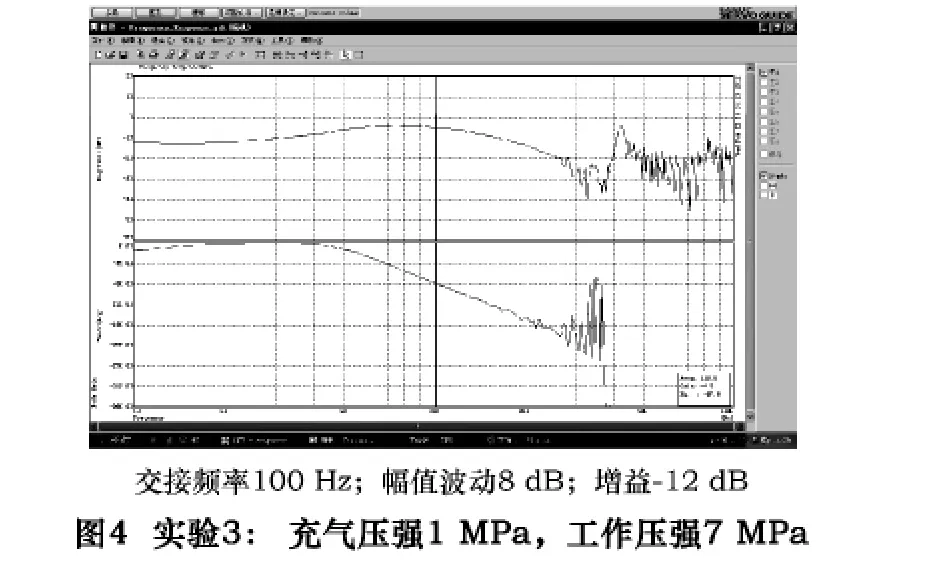
在圖2~5中,上半部分是幅頻特性,下半部分是相頻特性。其中橫軸是電動機輸入頻率,交接頻率是相位在-90°時的頻率,反映了ωn的高低;縱軸是系統的對數幅值或相位,反映了增益的大小;兩條曲線的波動反應了系統輸出的平穩性。
對圖2~5圖形進行比較,不難發現圖5所代表的伺服傳動系統性能在中、低頻段最好;而此高頻段的性能可通過數控系統中的HRV濾波器進行校正。所以圖5是蓄能器平衡回路各參數設置的最佳狀態。
下面對圖2~5進行具體分析:
(1)平衡回路中油液多少對系統頻率的影響
在圖2~5中,因為平衡系統內油液多少的不同,引起各伺服系統交接頻率的不同:圖2中135Hz,圖3中125Hz,圖4中100Hz。由此可見,回路中油量越少時,伺服傳動系統的固有頻率ωn越高,從而頻寬越大;而頻寬近似地正比于響應速度,所以響應速度越快,響應時間越短,如圖2所示。
(2)平衡回路中油液多少對系統阻尼比的影響
同樣從圖2~4中可以看到,當蓄能器選定、充氣壓強設定的情況下,平衡回路內的油液越多時,油缸內實際工作壓強越大,伺服傳動系統的阻尼比ζ越小,增益越大,如圖4所示。
(3)蓄能器充氣壓強對系統增益及平穩性的影響
比較圖3與圖5的各參數,容易分析出同樣的蓄能器在不同的充氣壓強下,增益不同。當充氣壓強越大時,伺服系統不但增益越大,而且增益的波動性越小,即系統越平穩,如圖5所示。
3 結語
比較第一與第二部分的分析結果,二者基本一致;并且發現,蓄能器內充氣壓強、工作壓強的高低對伺服傳動系統增益的大小及其波動性影響較大,而蓄能器與連接管路中油液的多少對系統的頻率影響較大。
為了使數控機床獲得較高的固有頻率,以及良好的運動平穩性,在設計蓄能器平衡重量的回路時,應做如下考慮:首先,在主軸組重量一定的前提下,選擇較高的工作壓強及充氣壓強;其次,優先選擇矮胖型的蓄能器并垂直安裝;最后,蓄能器與平衡油缸之間采用大直徑小管長的連接方式。
按上述結論,對機床的平衡系統調整改進后,明顯提高了被加工件的精度,尤其是輪廓跟隨精度。
[1]官忠范.液壓傳動系統[M].3版.北京:機械工業出版社,2011.
[2]楊位欽,謝錫祺.自動控制理論基礎[M].北京:北京理工大學,1991.

