單儲絲筒線切割機的切割線振動研究*

張國慶 趙則祥 于賀春 張 洪 張楚鵬

(中原工學院機電學院，河南鄭州 451191)

在對特殊晶體進行線切割加工時，切割線的振動和切割方向的頻繁改變會對晶體的切割精度造成很大影響。切割線的振動主要由張力波動產生，而引起切割線張力波動的因素有很多，如勻速切割過程中切割阻力的變化、變速切割過程中切割速度的大小和方向的改變以及在整個切割過程中張力調節裝置對切割線的影響。對切割線的張力波動進行控制可以減小切割線在工作過程中的振動，進而提高加工精度。張義兵等人［1］分析了張力錘結構對張力波動的影響，并設計了一種對張力波動影響較小的控制系統。蔣近等人［2］提出了減小張力擺桿結構對張力波動影響的方法，并設計了基于相鄰軸誤差的多電動機同步控制系統。黃潔等人［3］對張力的自適應控制方法進行了仿真研究，設計了一種精度較高的張力控制算法。

在目前已知的張力控制方法中，絕大多數是通過控制非切割區域的張力來間接調節切割區域的張力，而由于切割線導向輪存在轉動慣量，使得張力調節出現遲滯，不能達到預期的效果。而針對導向輪轉動慣量對切割線振動的影響方面的研究，國內外尚未見報道。本文建立了基于單儲絲筒線切割機床走絲系統的數學模型，推導出在切割阻力作用下切割線的長度及彎曲角度的變化公式，在Matlab的Simulink環境下建立仿真模型，并運行求解，結果揭示了導向輪轉動慣量和切割阻力對切割線振動的影響規律。

1 走絲系統的總體結構

單儲絲筒線切割機為單線切割，切割線為金屬絲或鍍金剛石微粒金屬絲，主要用于特殊晶體的切割，對切割質量要求很高。

圖1為單儲絲筒線切割機走絲系統的結構簡圖。絕大部分的切割線繞在儲絲筒上，其余部分繞過張緊輪、導向輪最后回到儲絲筒。切割工件時儲絲筒由電動機帶動旋轉，張緊輪和導向輪在切割線的帶動下同時轉動，由于受到工件帶來的切割阻力的影響，兩個導向輪之間的切割線會發生彎曲，兩個張力擺桿機構的擺動角度隨之改變。

2 轉動慣量對切割線振動的影響

由于儲絲筒同時完成收放線工作，在假設切割線不可延長的前提下，未被纏繞在儲絲筒上線的總長度保持不變。在勻速切割過程中，如果沒有切割阻力，則各導向輪和張緊輪的轉速恒定且張力擺桿的擺動角度不變，切割線的張力處處相等，走絲系統處于一個相對穩定的狀態。而由于兩個導向輪之間的切割線在切割工件時受到切割阻力，使得此段切割線的張力增大，大于儲絲筒與導向輪之間切割線的張力，導向輪由于受力不均轉速發生改變。兩個導向輪之間的切割線的長度增加，則儲絲筒與導線輪之間的切割線的長度同時減小。

在不考慮各輪轉動摩擦力和切割線重力的前提下，如果張緊輪和導向輪的轉動慣量為零，則兩個導向輪之間的切割線的張力變化能在瞬間傳到儲絲筒與導向輪之間的切割線上，使得各處張力同時變化且處處相等。由于轉動慣量的存在，使得張力的傳遞出現了遲滯，成為引起切割線振動的一個主要因素。

3 轉動慣量的分析模型

3.1 數學模型的建立與分析

為了分析轉動慣量對切割線振動的影響，本文建立了一個走絲系統的簡化的模型，如圖2所示。為簡化后期計算，模型中設定儲絲筒與兩個導向輪的直徑相等，用理想的恒力FP代替張力擺桿裝置，FP作用在儲絲筒與導向輪之間切割線的中點上，方向垂直于儲絲筒與導向輪的中心連線。模型中將工件帶來的切割阻力簡化為一個方向垂直向上的變力FM，FM作用在兩個導向輪之間切割線的中點上，其大小模擬真實情況下的切割阻力。儲絲筒與導向輪的中心距記為L，兩個導向輪之間的中心距記為L＇。

初始狀態下，此模型中儲絲筒和導向輪均靜止，切割阻力FM為零，儲絲筒與導向輪之間的切割線在恒力FP的作用下達到最大彎曲程度，兩個導向輪之間的線無彎曲，切割線的張力處處相等。之后隨著FM的變化，各段切割線的長度和張力均發生變化。

圖3為儲絲筒部分的分析示意圖。圖中線段AB為儲絲筒與導向輪1的公切線上的一段，A點為切點。C點為切割線與儲絲筒的切點，D點為恒力FP的作用點，儲絲筒與導向輪間的切割線的拉力記為FT，弧AC為切割線纏繞在儲絲筒上的部分，切割線線段CD與AB的夾角為α，儲絲筒的半徑記為r。

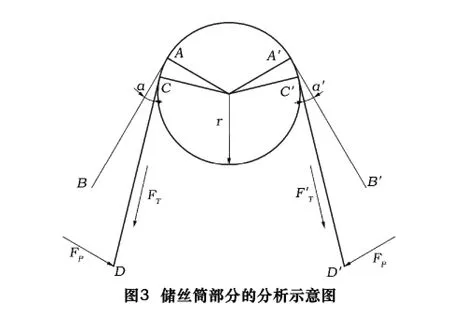
圖4為導向輪1部分的分析示意圖，字符的定義方法與圖3類似。由于在此模型中，導向輪1與2的受力情況相同，故本文中只對導向輪1做分析。

儲絲筒與導向輪1的公切線的切點間的切割線的長度為

兩個導向輪間的切割線的長度為

式中:α和β的單位均為rad。

適用于導向輪的轉動慣量公式為

使導向輪轉動的力為

則導向輪轉動的線加速度為

在此模型中，隨著切割阻力FM的變化，各部分切割線的彎曲角度α和β也會變化。設在t時刻，α和β的大小分別為αt和βt，導向輪的轉速為vt，經過Δt時刻之后，α 和 β 的大小分別為 αΔt和 βΔt。設 Δt為無窮小，則在此段時間內，導向輪轉動的弧長為

設在t時刻，儲絲筒與導向輪之間切割線的總長度為L1t，兩個導向輪之間切割絲的總長度為L2t，到t+ Δt時刻切割線的長度分別變為L1Δt和L2Δt，則有

結合公式(1)、(2)、(7)、(8)可得

式(9)和(10)反映了導向輪的轉動對切割線彎曲角度的影響，而導向輪的轉動規律由切割阻力FM決定，利用Simulink的動態仿真功能可以得出在FM作用下的導向輪轉動慣量對切割線振動的影響。

3.2 Simulink仿真模型的建立與分析

根據式(6)、(9)、(10)建立的Simulink仿真模型如圖5所示。在此模型中設定輸入的切割阻力及其他相關參數，運行求解后即可得出導向輪轉動慣量對切割線振動的影響。

4 運行求解

4.1 初始條件的設定

結合實際情況，在運行求解前將初始條件設定為:L=1.2 m，L′=1.0 m，r=0.1 m，m=0.1 kg，α =π/18，β=0。FM輸入的是一個半周期正弦波，其振幅為20，頻率為1/1 200，仿真求解時間為600 s。

4.2 仿真結果

Simulink模型運行后，各示波器輸出的波形如圖6所示。

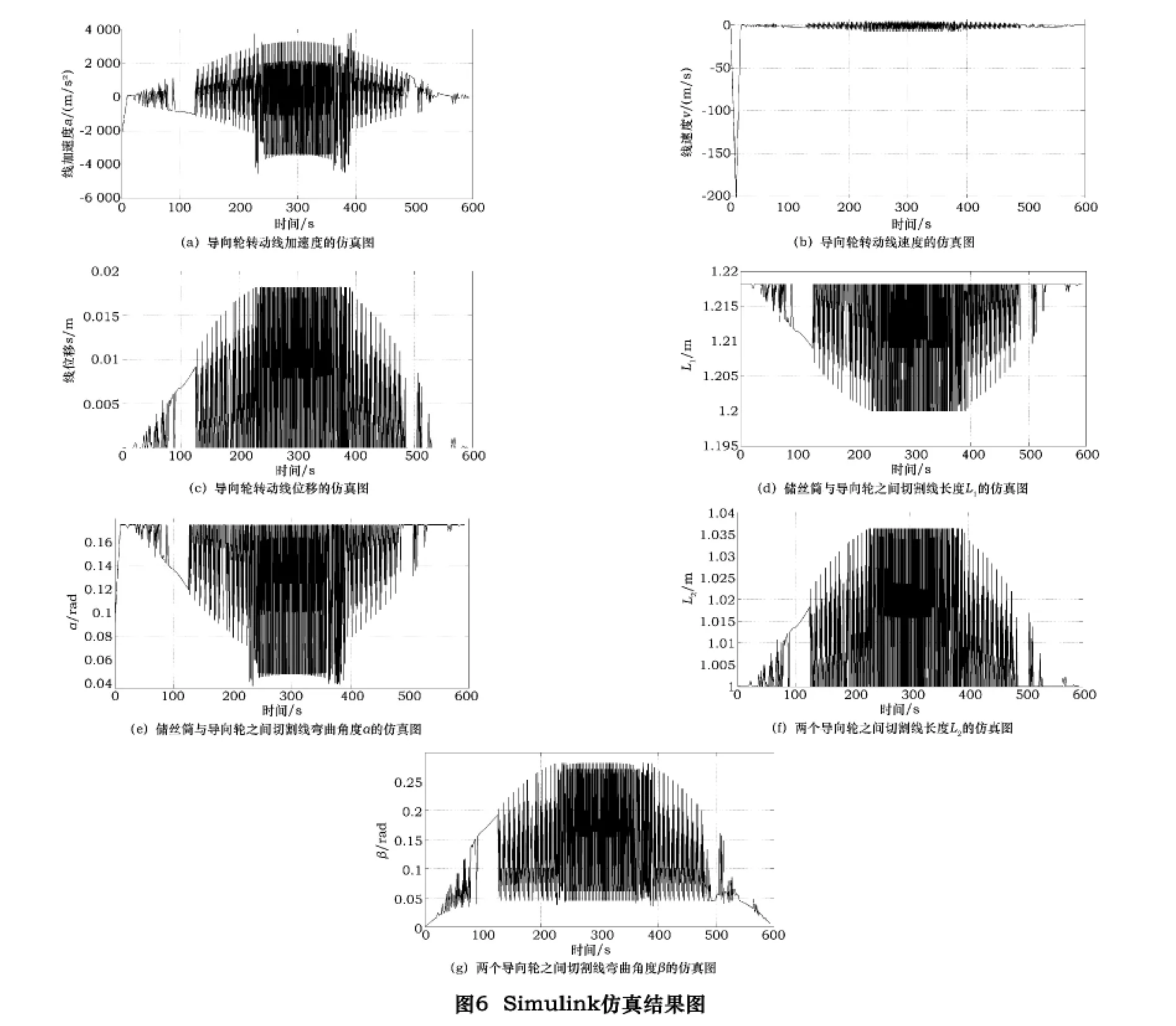
由圖6可以看出，導向輪在切割線的帶動下其線加速度、線速度和線位移時刻發生著變化，同時兩個導線輪之間的切割線的彎曲角度β也在不斷變化。角度β的變化反映了切割線的振動情況，其變化趨勢與切割阻力的變化趨勢大體一致，其幅值與導向輪質量近似成反比關系。

5 結語

(1)導向輪轉動慣量的存在是切割線在工作過程中發生振動的主要原因。

(2)切割阻力的變化規律對切割線的振動規律有決定作用。

(3)減輕導向輪的重量可以提高切割線振動的靈敏度，雖然此時切割線振動頻率更高，但是振幅會減小，在實際加工過程中更有利于提高工件表面質量。

［1］張義兵，戴瑜興，袁巨龍，等.多線切割機線張力控制系統設計實現［J］.機械工程學報，2009，45(5):295 －300.

［2］蔣近，戴瑜興，郜克存，等.多線切割機線走線系統的張力控制［J］.機械工程學報，2011，47(5):183 －187.

［3］黃潔，李偉.多線切割機線張力自適應控制仿真研究［J］.機械科學與技術，2012，31(3):437 －441.