基于層次分析法的國家助學(xué)金多級(jí)模糊綜合評(píng)價(jià)

耿悅敏

基于層次分析法的國家助學(xué)金多級(jí)模糊綜合評(píng)價(jià)

耿悅敏

國家助學(xué)金的評(píng)定受到諸多因素影響，加之評(píng)定條件本身屬于模糊概念，造成一定程度的主觀因素過強(qiáng)、信息不對(duì)稱。為客觀、公正、合理、規(guī)范地對(duì)申請(qǐng)國家助學(xué)金的學(xué)生進(jìn)行評(píng)價(jià)，本文運(yùn)用模糊系統(tǒng)理論，建立多級(jí)模糊綜合評(píng)價(jià)體系，并運(yùn)用層次分析法確定了評(píng)價(jià)指標(biāo)的權(quán)重。由于充分考慮了評(píng)價(jià)指標(biāo)的模糊因素，很大程度上降低了主觀因素的影響，使評(píng)定結(jié)果更客觀公正。

國家助學(xué)金；層次分析法；模糊系統(tǒng)；多級(jí)模糊綜合評(píng)價(jià)

耿悅敏/廣東交通職業(yè)技術(shù)學(xué)院講師（廣東廣州 510650）。

一、引言

為體現(xiàn)黨和政府對(duì)普通本科高校、高等職業(yè)學(xué)校家庭經(jīng)濟(jì)困難學(xué)生的關(guān)懷，幫助他們順利完成學(xué)業(yè)，根據(jù)《國務(wù)院關(guān)于建立健全普通本科高校、高等職業(yè)學(xué)校和中等職業(yè)學(xué)校家庭經(jīng)濟(jì)困難學(xué)生資助政策體系的意見》（國發(fā)[2007]13號(hào)），決定在高等教育階段建立起國家助學(xué)金等對(duì)高校家庭經(jīng)濟(jì)困難學(xué)生資助政策體系。政策實(shí)施五年來，國家助學(xué)金的評(píng)選出現(xiàn)了一些不容忽視的問題：部分非貧困生擠占助學(xué)金名額；獲資助的學(xué)生也并非都是貧困生；少數(shù)貧困生感情受到傷害[1]。分析問題形成的原因，主要在于現(xiàn)有國家助學(xué)金評(píng)定條件的實(shí)際操作性不強(qiáng)，如國家助學(xué)金主要用于資助“貧困生”，然而“貧困生”的認(rèn)定難度卻很大。作為評(píng)定的重要指標(biāo)之一，“貧困”本身就屬于模糊的概念，加之當(dāng)前“貧困生”的認(rèn)定主要采用定性而非定量的方法，造成一定程度的主觀因素過強(qiáng)、信息不對(duì)稱。如何客觀、公正、合理、規(guī)范地對(duì)申請(qǐng)國家助學(xué)金的學(xué)生進(jìn)行評(píng)價(jià)，使國家助學(xué)金的發(fā)放，既能真正解決貧困學(xué)生的實(shí)際困難，讓品學(xué)兼優(yōu)的貧困生得到切實(shí)的資助，又能最大限度地發(fā)揮助學(xué)金對(duì)貧困生的激勵(lì)和教育作用，已成為現(xiàn)階段亟待解決的問題。

二、問題分析

國家助學(xué)金的設(shè)立是為激勵(lì)普通本科高校、高等職業(yè)學(xué)校學(xué)生勤奮學(xué)習(xí)，努力進(jìn)取，在德、智、體、美等方面得到全面發(fā)展，體現(xiàn)黨和政府對(duì)家庭經(jīng)濟(jì)困難學(xué)生的關(guān)懷，幫助他們順利完成學(xué)業(yè)而采取的重大舉措。其申請(qǐng)條件：（1）熱愛社會(huì)主義國家，擁護(hù)中國共產(chǎn)黨的領(lǐng)導(dǎo)；（2）遵守憲法和法律，遵守學(xué)校各項(xiàng)規(guī)章制度；（3）誠實(shí)守信，道德品質(zhì)優(yōu)良；（4）勤奮學(xué)習(xí)，積極上進(jìn)；（5）家庭經(jīng)濟(jì)困難，生活儉樸。由此可見，國家助學(xué)金的資助對(duì)象是“貧困生”，條件還要求“勤奮學(xué)習(xí)，積極上進(jìn)”。但“貧困”、“勤奮”和“積極”本身都屬于模糊概念，所謂模糊是指客觀事物差異的中間過渡中的“不分明性”或“亦此亦彼性”[2]。 例如“貧困”與“不貧困”、“勤奮”與“不勤奮”、“積極”與“不積極”之間沒有絕對(duì)分明和固定不變的界限，這些現(xiàn)象就很難用經(jīng)典的數(shù)學(xué)方法進(jìn)行描述。因此，本文利用模糊數(shù)學(xué)和綜合評(píng)價(jià)的理論與方法，同時(shí)運(yùn)用層次分析法確定評(píng)價(jià)指標(biāo)的權(quán)重，建立國家助學(xué)金多級(jí)模糊綜合評(píng)價(jià)體系。

三、評(píng)價(jià)方法及原理

（一）層次分析法理論

20世紀(jì)70年代美國著名運(yùn)籌學(xué)家T·L·Saaty等人提出了一種多目標(biāo)、多準(zhǔn)則的決策方法——層次分析法（Analytic Hierarchy Process,簡記AHP）。它能將一些量化困難的定性問題在嚴(yán)格數(shù)學(xué)運(yùn)算基礎(chǔ)上定量化；將一些定量、定性混雜的問題綜合為統(tǒng)一整體進(jìn)行綜合分析。這種方法在解決問題時(shí)，可對(duì)定性、定量之間轉(zhuǎn)換、綜合計(jì)算等解決問題過程中人們所作判斷的一致性程度等問題進(jìn)行科學(xué)檢驗(yàn)[3]。

（二）基于層次分析法的評(píng)價(jià)指標(biāo)權(quán)重確定[4]

根據(jù)影響評(píng)價(jià)對(duì)象的主要因素，建立系統(tǒng)的遞階層次結(jié)構(gòu)以后，需要運(yùn)用層次分析法確定各評(píng)級(jí)指標(biāo)的權(quán)重，大體可分為四個(gè)步驟進(jìn)行：

第一，以上一層次某因素為準(zhǔn)，它對(duì)下一層次諸因素有支配關(guān)系，兩兩比較下一層次諸因素對(duì)它的相對(duì)重要性，并賦予一定分值，一般采用Saaty教授提出的1-9尺度法，見表1所示。

表1 1-9尺度的含義

第二，由判斷矩陣計(jì)算被比較元素對(duì)于該準(zhǔn)則的相對(duì)權(quán)重。依據(jù)判斷矩陣求解各層次指標(biāo)子系統(tǒng)或指標(biāo)項(xiàng)的相對(duì)權(quán)重，就是計(jì)算判斷矩陣最大特征根及其對(duì)應(yīng)的特征向量。以判斷矩陣A為例，即由

其中A為判斷矩陣；λ為特征根；ω為特征向量，解出λmax及對(duì)應(yīng)的ω。將λmax所對(duì)應(yīng)的最大特征向量歸一化，就得到下一層相對(duì)于上一層的相對(duì)重要性的權(quán)重值。

第三，一致性檢驗(yàn)。用判斷矩陣最大特征根以外其余特征根的負(fù)平均值，作為度量建立判斷矩陣過程中所作的所有兩兩比較判斷偏離一致性程度的指標(biāo)CI（Consistency Index）。

其中n為判斷矩陣階數(shù)；λmax為判斷矩陣最大特征根。判斷矩陣一致性程度越高，CI值越小。當(dāng)CI=0時(shí)，判斷矩陣達(dá)到完全一致。

Saaty又引入隨機(jī)一致性指標(biāo)RI來修正CI，將它的一致性指標(biāo)CI與同階的隨機(jī)一致性指標(biāo)RI之比稱為一致性比率CR，當(dāng)CR＜0.1時(shí)認(rèn)為A的不一致程度在允許范圍內(nèi)，可用其特征向量作為權(quán)向量。否則要重新進(jìn)行成對(duì)比較，對(duì)A加以調(diào)整。

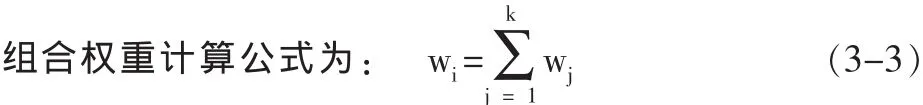
第四，計(jì)算各層因素對(duì)系統(tǒng)的組合權(quán)重，并進(jìn)行排序其中wij為第i個(gè)指標(biāo)第j層的權(quán)重值：k為總層數(shù)。

每個(gè)判斷矩陣一致性檢驗(yàn)通過并不等于整個(gè)遞階層次結(jié)構(gòu)所做判斷具有整體滿意的一致性。因此還要進(jìn)行整體一致性檢驗(yàn)。

（三）多級(jí)模糊綜合評(píng)價(jià)方法原理

高等院校國家助學(xué)金的評(píng)定受諸多因素的影響，是一個(gè)多層次、多因素的綜合評(píng)價(jià)問題，需要全面地反映家庭經(jīng)濟(jì)困難學(xué)生的實(shí)際情況，有很多指標(biāo)很難用經(jīng)典的數(shù)學(xué)進(jìn)行分析，所以本文選擇多級(jí)模糊綜合評(píng)價(jià)法建模。

多級(jí)模糊綜合評(píng)價(jià)的基本步驟[5]：

1.給出被評(píng)價(jià)對(duì)象集合 X={x1，x2，x3,…xi}；

2.確定因素集（即評(píng)價(jià)指標(biāo)體系）U={u1，u2，u3,…un}，國家助學(xué)金評(píng)定考慮的因素很多，將U按各屬性分解成S個(gè)子集：Ui={ui1，ui2，ui3,…uin}（i=1,2,…s），且滿足條件：

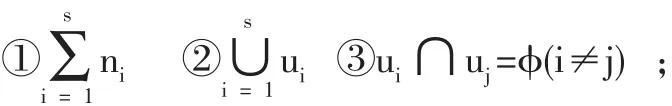
3.建立評(píng)語集 V={v1，v2，v3,…vm}；

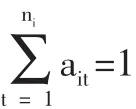
四、模型建立

（一）國家助學(xué)金評(píng)價(jià)指標(biāo)體系的構(gòu)建

本評(píng)價(jià)指標(biāo)體系的構(gòu)建以現(xiàn)行國家助學(xué)金評(píng)定條件為依據(jù)，同時(shí)遵循以下原則[6]：①導(dǎo)向性原則；②全面性原則；③過程性評(píng)價(jià)與終結(jié)性評(píng)價(jià)相結(jié)合原則；④個(gè)性化原則；⑤可操作性原則，同時(shí)結(jié)合實(shí)際評(píng)比中容易出現(xiàn)和遺漏的問題，主要從四個(gè)方面構(gòu)建國家助學(xué)金綜合評(píng)價(jià)指標(biāo)體系，如表2所示（表中權(quán)重由表4評(píng)價(jià)指標(biāo)權(quán)重的確定算得）。

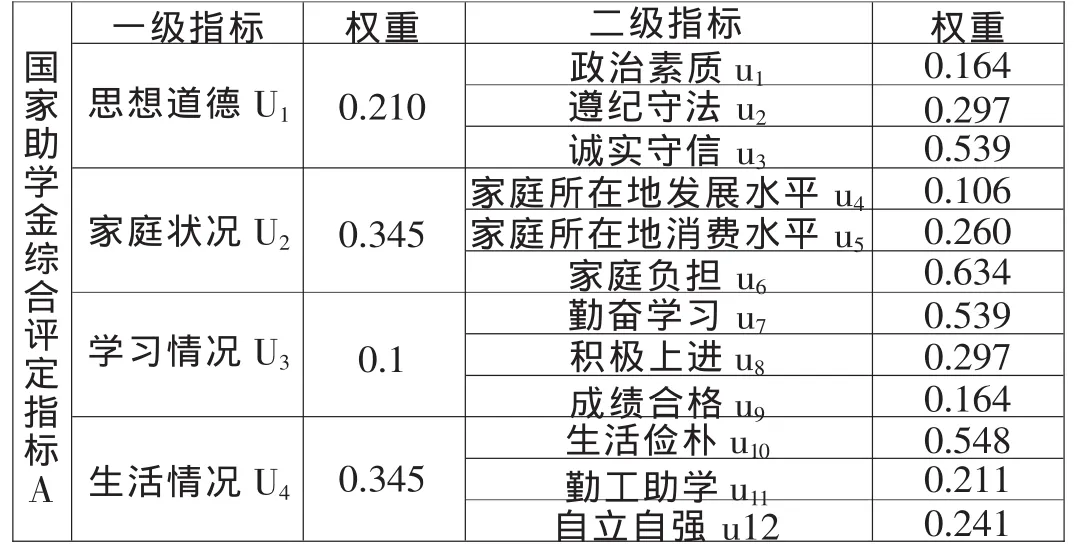
表2 國家助學(xué)金綜合評(píng)定指標(biāo)

（二）建立評(píng)語集V

V={v1（很好），v2（較好），v3（一般），v4（不好）}，其中，vi（i=1，2，3，4）表示第 i個(gè)評(píng)價(jià)等級(jí).用專家咨詢法確定 100～90 分為優(yōu)秀，89～80 為良好，79～70 為一般，69～60 為較差。 將評(píng)語集的等級(jí)用1分制數(shù)量化，得到評(píng)價(jià)等級(jí)向量V'={1，0.8，0.5，0.3}。

（三）評(píng)價(jià)指標(biāo)權(quán)重的確定

采用層次分析法確定權(quán)重，首先構(gòu)造比較判斷矩陣。由專家根據(jù)1-9尺度法將指標(biāo)進(jìn)行兩兩比較，得出判斷矩陣；其次對(duì)判斷矩陣進(jìn)行運(yùn)算和正規(guī)化處理；最后對(duì)判斷矩陣進(jìn)行一致性檢驗(yàn)。結(jié)果如表3所示。

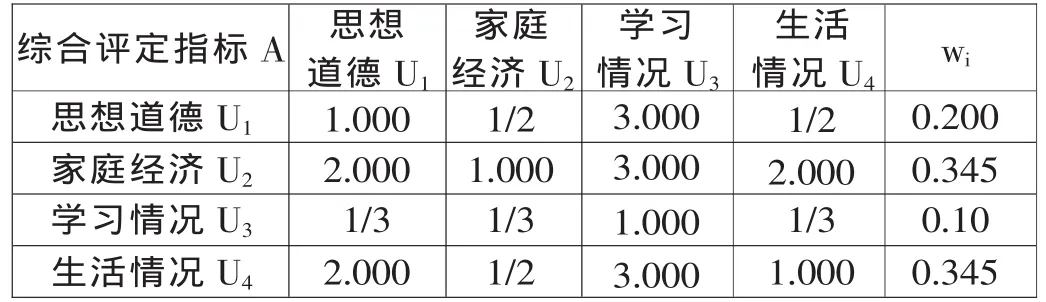
表3U 層對(duì)目標(biāo)層A的判斷矩陣及權(quán)重計(jì)算

運(yùn)用相同的方法進(jìn)一步對(duì)整個(gè)指標(biāo)體系進(jìn)行計(jì)算，得到了如下的指標(biāo)體系的判斷矩陣和權(quán)重計(jì)算，見表4，5，6,7。

表4u 層對(duì)目標(biāo)層U1層的判斷矩陣和權(quán)重計(jì)算

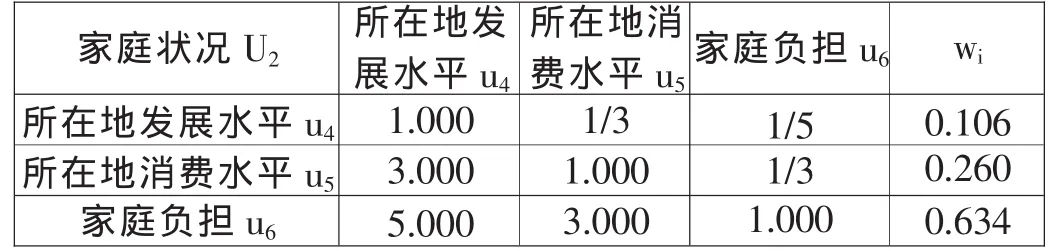
表5u 層對(duì)目標(biāo)層U2層的判斷矩陣和權(quán)重計(jì)算

表6u 層對(duì)目標(biāo)層U3層的判斷矩陣和權(quán)重計(jì)算

表7u 層對(duì)目標(biāo)層U4層的判斷矩陣和權(quán)重計(jì)算

（四）模糊評(píng)價(jià)矩陣的建立

本模型由評(píng)定小組根據(jù)評(píng)判集對(duì)申請(qǐng)人進(jìn)行評(píng)判，由評(píng)判結(jié)果構(gòu)造出每個(gè)因素的評(píng)判和模糊矩陣。如記第i個(gè)二級(jí)因素的評(píng)判為（ri1，ri2，ri3，ri4）（i=1，2，3，4），則相應(yīng)一級(jí)因素的模糊評(píng)價(jià)矩陣為

（五）多級(jí)模糊綜合評(píng)價(jià)

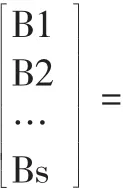
一級(jí)模糊綜合評(píng)價(jià)：Bi=Ai×Ri，（i=1，2，3， 4）。

二級(jí)模糊綜合評(píng)價(jià)：B=A×R，

為方便排序比較，將模糊綜合評(píng)價(jià)值轉(zhuǎn)化為一個(gè)確定的標(biāo)量值:b=V'×BT。

（六）評(píng)價(jià)結(jié)果處理及應(yīng)用

以本班申請(qǐng)國家助學(xué)金的同學(xué)甲為例，通過評(píng)定小組的評(píng)價(jià)，運(yùn)用上述方法建立的模糊評(píng)價(jià)綜合評(píng)價(jià)體系進(jìn)行綜合評(píng)價(jià)，得到如下結(jié)果：

一級(jí)模糊綜合評(píng)價(jià)：B1=A1×R1=[0.827 0.173 0 0]，B2=A2×R2=[0.623 0.273 0.104 0]，B3=A3×R3=[0.606 0.364 0.03 0]，B4=A4×R4=[0.667 0.23 0.103 0]。

二級(jí)模糊綜合評(píng)價(jià)：B=A×E=[0.68 0.25 0.07 0]。

對(duì)應(yīng)評(píng)價(jià)等級(jí)向量 V'={1，0.8，0.5，0.3}， 可將模糊綜合評(píng)價(jià)值轉(zhuǎn)化為一個(gè)確定的標(biāo)量值:b=V'×BT=[1 0.8 0.5 0.3]×[0.68 0.28 0.07 0]T=0.915,

即該學(xué)生的模糊綜合評(píng)價(jià)值為0.915。

重復(fù)上述步驟即可得出各參評(píng)學(xué)生的模糊綜合評(píng)價(jià)值，從高到低依次排序，即可選出國家助學(xué)金的合適人選。

五、模型的分析與改進(jìn)

多級(jí)模糊綜合評(píng)價(jià)模型充分考慮了評(píng)價(jià)指標(biāo)的模糊因素，運(yùn)用模糊數(shù)學(xué)的方法對(duì)一些帶有模糊性的條件給出定量分析，很大程度上降低了主觀因素的影響，關(guān)于各因素的權(quán)重主要是依據(jù)實(shí)際背景主觀上給定的，實(shí)際操作時(shí)可以根據(jù)側(cè)重點(diǎn)適當(dāng)調(diào)整，不影響整體效果，并且本模型中詳細(xì)地分析了各因素之間的關(guān)系，利用AHP方法通過兩兩比較矩陣確定權(quán)向量，使評(píng)定結(jié)果更客觀公正。因此，本模型還可應(yīng)用到獎(jiǎng)學(xué)金、三好學(xué)生等各類評(píng)比項(xiàng)目。

本模型仍需改進(jìn)之處：利用AHP方法通過兩兩比較矩陣確定權(quán)向量時(shí)，結(jié)果雖然更客觀，但需要大量的計(jì)算，如果單純依賴人工完成，其工作量之大可想而知，因此，未來可以考慮利用計(jì)算機(jī)輔助建立起綜合測評(píng)系統(tǒng)，操作人員只需將評(píng)定小組給出的評(píng)定結(jié)果輸入計(jì)算機(jī)就可完成綜合評(píng)價(jià)的全過程,從而使國家助學(xué)金的評(píng)定體系更加完善，評(píng)定結(jié)果更加科學(xué)、公正。

：

[1]郭昕，田輝玉.國家助學(xué)金評(píng)選面臨的問題與對(duì)策[J].教育與經(jīng)濟(jì)，2011：（4）：38-40

[2]劉煥彬等.數(shù)學(xué)模型與實(shí)驗(yàn)[M].北京：科學(xué)出版社，2008：157-182

[3]萬遠(yuǎn)英，尹德志．大學(xué)生綜合素質(zhì)層次分析評(píng)價(jià)體系及其數(shù)學(xué)模型[J]．西南民族大學(xué)學(xué)報(bào)（人文社科版），2003，24（12）：191-193

[4]夏怡新．構(gòu)建高校學(xué)生綜合素質(zhì)評(píng)價(jià)體系的思考[J]．教育探索，2003（8）：53-5

[5]謝季堅(jiān)，劉承平.模糊數(shù)學(xué)方法及其應(yīng)用[M].武漢：華中科技大學(xué)出版社，2000：197-215

[6]胡慶宇.基于層次分析法的大學(xué)生綜合素質(zhì)多級(jí)模糊評(píng)價(jià)[D].保定：華北電力大學(xué)，2010：33-40

O029

A

1671-6531（2013）16-0134-03

責(zé)任編輯：姚 旺