短波自適應(yīng)通信的信道仿真算法研究

范 偉， 朱家成， 胡 飛

（中國(guó)電子科技集團(tuán)公司第三十研究所，四川 成都 610041）

0 引言

為改善短波通信質(zhì)量，能夠動(dòng)態(tài)適應(yīng)短波信道變化情況，基于自適應(yīng)選頻技術(shù)和自適應(yīng)編碼調(diào)制技術(shù)的短波自適應(yīng)通信技術(shù)得到人們廣泛研究[1]，成為國(guó)內(nèi)外熱點(diǎn)研究課題。法國(guó)Thales公司成功研發(fā)了短波自適應(yīng)通信系統(tǒng)System-3000。短波通信中不可預(yù)測(cè)的信道變化特征使得通過(guò)實(shí)際線路測(cè)試來(lái)獲取可重復(fù)性驗(yàn)證結(jié)果變得幾乎不太可能。因此，短波自適應(yīng)通信系統(tǒng)設(shè)計(jì)者首先就需要建立適用的短波信道理論模型，利用理論分析的方法準(zhǔn)確地、可重復(fù)性地分析系統(tǒng)的性能。

Watterson信道模型是目前被廣泛接受的窄帶短波信道模型（信道帶寬小于12 kHz），通常認(rèn)為其可以準(zhǔn)確秒量級(jí)刻畫短波信道特點(diǎn)，目前已經(jīng)被廣泛用于理論評(píng)估短波調(diào)制解調(diào)器性能[2-3]。短波信道的一天內(nèi)各時(shí)段或者更長(zhǎng)時(shí)間上變化可以通過(guò)VOACAP、ICEPAC等[4]軟件進(jìn)行較好地預(yù)測(cè)，這類研究屬于短波頻率預(yù)報(bào)研究范疇。而短波自適應(yīng)通信系統(tǒng)采用自適應(yīng)通信技術(shù)來(lái)匹配動(dòng)態(tài)信道，與短波波形性能評(píng)估和短波頻率預(yù)報(bào)不同，在理論性能評(píng)估時(shí)，希望建立的信道模型是能夠刻畫分鐘量級(jí)等較長(zhǎng)時(shí)間周期內(nèi)的短波信道質(zhì)量變化情況。

針對(duì) Watterson模型無(wú)法刻畫短波信道中期變化特征（ITV，Intermediate Terms Variations）和長(zhǎng)期變化特征（LTV，Long Terms Variations），F(xiàn)urman等[5]通過(guò)統(tǒng)計(jì)數(shù)日內(nèi)的短波天線線路測(cè)試的信道質(zhì)量參數(shù)，得出每10秒內(nèi)的信噪比變化服從標(biāo)準(zhǔn)差為4 dB的對(duì)數(shù)正態(tài)分布，其自相關(guān)特性具有指數(shù)型，2007年美國(guó)Harris研究人員[6]提出了一種可用于驗(yàn)證短波數(shù)據(jù)鏈路協(xié)議性能的刻畫短波信道中長(zhǎng)期變化特征的信道仿真算法。

基于Watterson模型和Furman等研究結(jié)果，文中提出了一種純軟件的短波信道仿真方案。該算法具有全數(shù)字化特點(diǎn)，可實(shí)時(shí)集成到短波自適應(yīng)調(diào)制解調(diào)器中以滿足短波自適應(yīng)通信系統(tǒng)測(cè)試需要，具有重要的實(shí)際應(yīng)用價(jià)值。

1 Watterson信道模型

Watterson短波信道模型采用高斯散射增益抽頭延遲線模型，其原理框圖如圖1所示，其中延遲器和相加器表征了具有不同多徑延遲的短波多徑傳播效應(yīng)。短波信道上的加性噪聲和各種干擾通過(guò)相加器體現(xiàn)。乘法器表示了在短波信道的各條多徑路徑上的時(shí)變色散衰落特性，用路徑增益函數(shù)來(lái)表示。

圖1 Watterson信道模型原理示意

路徑增益函數(shù)是 Watterson信道模型的關(guān)鍵部分，可以表示為：

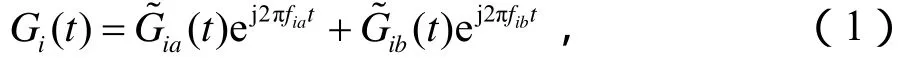
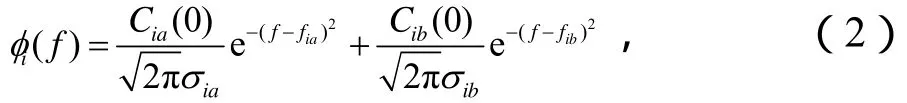
式中，iaf和ibf為第i條路徑的多普勒頻移，iaσ和ibσ為第i條路徑的多普勒擴(kuò)展。

2 Watterson模型軟件仿真算法

基于Watterson模型的短波信道軟件仿真如圖2所示。信號(hào)經(jīng)過(guò)Hilbert變換后分為相位相差90度的兩路信號(hào)，根據(jù)仿真所需路徑數(shù)選擇相應(yīng)的路徑延遲。每條路徑中獨(dú)立考慮多普勒擴(kuò)展和多普勒頻移。所得路徑的實(shí)部相加，作為輸出信號(hào)。為了設(shè)置相應(yīng)的信噪比，在輸入端對(duì)信號(hào)和噪聲進(jìn)行功率測(cè)量，根據(jù)所得信號(hào)強(qiáng)度和所要求的信噪比來(lái)設(shè)置噪聲源的強(qiáng)度，然后與多徑輸出信號(hào)相加，即為信道仿真輸出。

短波Watterson軟件仿真主要對(duì)以下3個(gè)方面來(lái)實(shí)現(xiàn)：各徑獨(dú)立設(shè)置相應(yīng)的時(shí)延；短波衰落傳播效應(yīng)仿真：采用預(yù)設(shè)多普勒頻移和多普勒擴(kuò)展來(lái)改變多徑路徑增益系數(shù)；噪聲環(huán)境仿真：噪聲源輸出噪聲或者輸入信號(hào)乘上特定增益系數(shù)來(lái)獲取不同信噪比，在某次測(cè)試中其信噪比通常是固定的。

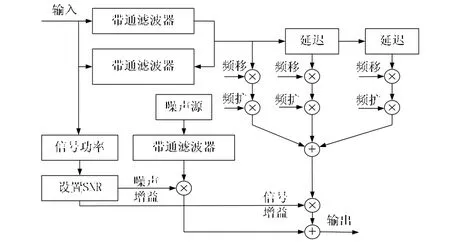
圖2 短波Watterson模型軟件仿真總體方案

其中短波衰落傳播效應(yīng)仿真算法設(shè)計(jì)至關(guān)重要。多普勒頻移主要是由于短波信道的多普勒效應(yīng)引起通信雙方載波頻率偏移，可通過(guò)在原始信號(hào)頻率基礎(chǔ)上疊加上一個(gè)預(yù)設(shè)多普勒頻率來(lái)模擬。多普勒擴(kuò)展則是反映路徑增益系數(shù)的時(shí)變特性，主要目的是產(chǎn)生短波信道沖擊響應(yīng)，其仿真準(zhǔn)確性將嚴(yán)重影響短波調(diào)制解調(diào)器性能理論評(píng)估的準(zhǔn)確性。多普勒擴(kuò)展仿真方案為：兩路相互獨(dú)立高斯噪聲源產(chǎn)生兩路高斯信號(hào)，這兩路高斯信號(hào)經(jīng)過(guò)兩個(gè)高斯低通濾波器后，合并形成短波信道復(fù)沖擊響應(yīng)，其中高斯低通濾波器帶寬對(duì)應(yīng)預(yù)設(shè)短波信道的多普勒擴(kuò)展帶寬。

3 仿真結(jié)果

根據(jù)ITU-R規(guī)定短波信道參數(shù)，仿真Watterson模型在不同多普勒擴(kuò)展的信道衰落情況。圖 3和圖4分別表示了多普勒擴(kuò)展為0.1 Hz和0.5 Hz情況下兩條短波傳播路徑的信道增益。從圖3和圖4中在40 s的仿真時(shí)間內(nèi)兩條徑的衰落情況與設(shè)置的多普勒擴(kuò)展是一致的，在一定程度上驗(yàn)證了模型的有效性和正確性。

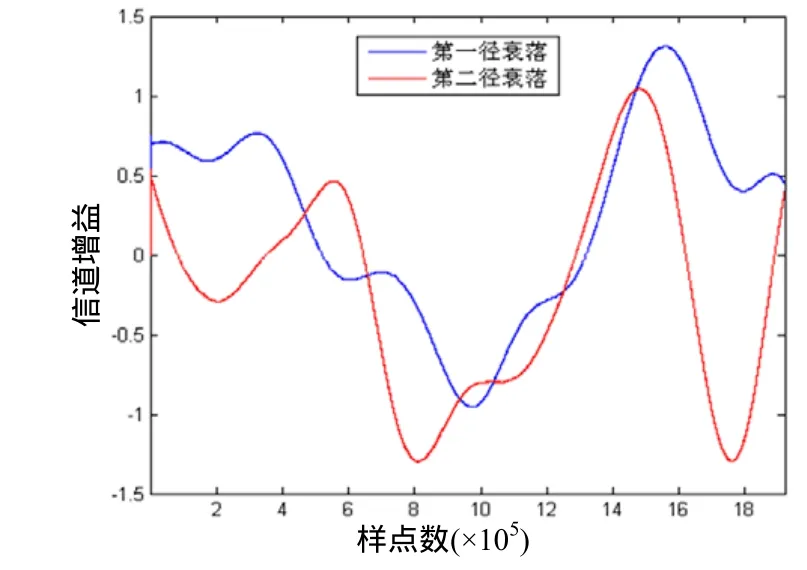
圖3 多普勒擴(kuò)展為0.1Hz時(shí)信道衰落

圖4 多普勒擴(kuò)展為0.5Hz時(shí)信道衰落

5 短波自適應(yīng)通信的信道仿真

短波自適應(yīng)通信性能的理論評(píng)估需要能夠準(zhǔn)確反映短波信道長(zhǎng)期變化趨勢(shì)（分鐘量級(jí)）的信道模型。Watterson信道模型以預(yù)設(shè)恒定信噪比來(lái)評(píng)估特定信噪比下的短波信號(hào)波形性能。而短波自適應(yīng)通信系統(tǒng)在信號(hào)波形傳輸周期內(nèi)，信噪比將呈現(xiàn)一個(gè)變化過(guò)程。因此，采用一個(gè)瞬時(shí)變化信噪比（SNR）來(lái)代替 Watterson信道模型中預(yù)設(shè)恒定不變信噪比是一個(gè)合理思路。

為驗(yàn)證短波數(shù)據(jù)傳輸鏈路性能，Harris公司基于 Watterson模型建立了具有時(shí)變信噪比特性的信道模型[6]，我們稱之為短波自適應(yīng)信道模型，其原理如圖5所示。

圖5 短波自適應(yīng)信道模型原理框

短波自適應(yīng)信道模型中,標(biāo)準(zhǔn) Watterson信道仿真器的固定信噪比被瞬時(shí)信噪比代替，時(shí)變信噪比反映了下面4個(gè)信道特性：

1）信噪比（SNR）的長(zhǎng)期變化趨勢(shì)。

2）信噪比（SNR）在 24小時(shí)周期內(nèi)的變化趨勢(shì)。

3）短波信道的長(zhǎng)期變化趨勢(shì)（LTV）。

4）短波信道的短期變化趨勢(shì)（ITV）。

每個(gè)瞬時(shí)信噪比由3部分相加得到：設(shè)置的平均信噪比、ITV信噪比時(shí)間序列、LTV信噪比時(shí)間序列。其中，LTV和ITV過(guò)程由具有指數(shù)自相關(guān)函數(shù)的對(duì)數(shù)正態(tài)分布隨機(jī)過(guò)程來(lái)模擬，并且相互獨(dú)立。

ITV和LTV可以由下面方法產(chǎn)生：由alpha濾波器對(duì)高斯噪聲進(jìn)行濾波，產(chǎn)生自相關(guān)函數(shù)呈指數(shù)分布的隨機(jī)噪聲。alpha濾波器可表示為：

高斯白噪聲通過(guò)該濾波器產(chǎn)生的序列具有指數(shù)型的自相關(guān)特性，而且自相關(guān)的時(shí)間常數(shù)取決于alpha的取值和序列的更新頻率。那么給定更新頻率，則通過(guò)調(diào)整 alpha的取值獲得需要的自相關(guān)特性。LTV信噪比時(shí)間序列采用的時(shí)間常數(shù)較大，而ITV采用時(shí)間常數(shù)則小得多。而通過(guò)調(diào)整ITV增益和LTV增益則可獲得需要的標(biāo)準(zhǔn)差。因此，該模型需要輸入5個(gè)參數(shù)：平均信噪比、ITV時(shí)間常數(shù)、ITV增益、LTV時(shí)間常數(shù)、LTV增益。

為獲得實(shí)際的短波信道ITV和LTV特征，Harris公司的Batts、Furman等進(jìn)行為期3天的短波天波線路試驗(yàn)[4]，兩地距離為 1 697 km。試驗(yàn)采用STANAG4538的BW5波形，每隔2.7 s發(fā)射一次。接收端評(píng)估并存儲(chǔ)每次的信噪比、多普勒擴(kuò)展、多徑等。對(duì)所估計(jì)信噪比時(shí)間序列（Nyquist頻率為0.185 Hz）進(jìn)行截止頻率為0.001 Hz的高通濾波，并且屏蔽短波信道信噪比一天不同時(shí)段以上的變化（周期大于90 min），再進(jìn)行截止頻率為0.01 Hz的高通濾波，得到短波信道信噪比的LTV時(shí)間序列（周期大于100 s）和ITV時(shí)間序列（周期大于5.4 s）。其結(jié)果為：

1）截止頻率0.001 Hz的高通濾波后，全天平均的信道信噪比變化的方差約為 24.8 dB2（標(biāo)準(zhǔn)差約為4.98 dB），其中6.3 dB2來(lái)自瑞利衰落（短期變化），其余則來(lái)自信道的ITV和LTV。

2）從信噪比時(shí)間序列的頻域上看，在 0.001～0.01 Hz范圍內(nèi)頻譜的峰值明顯且包絡(luò)大，表示明顯LTV特性。在0.01～0.185 Hz范圍內(nèi)包絡(luò)則不斷減小，表示ITV特性。

3）具有上述LTV和ITV特性的Watterson信道模型，通過(guò)合理設(shè)置參數(shù)，獲得與實(shí)際線路相似的秒量級(jí)和分鐘量級(jí)的變化特性。

因此，標(biāo)準(zhǔn)Watterson模型中具有上述LTV和ITV等時(shí)變信噪比特征的短波自適應(yīng)信道建模算法可以用來(lái)理論驗(yàn)證和分析短波自適應(yīng)通信系統(tǒng)性能。目前，正集成到我們研制的短波自適應(yīng)跳頻電臺(tái)系統(tǒng)中。

6 結(jié)語(yǔ)

文中對(duì)基于標(biāo)準(zhǔn) Watterson短波信道模型的短波信道模擬仿真系統(tǒng)進(jìn)行了軟件實(shí)現(xiàn)，短波信道多普勒擴(kuò)展效應(yīng)的結(jié)果表明算法軟件仿真的有效性和正確性。根據(jù)實(shí)際短波線路信道信噪比中長(zhǎng)期變化特性，提出基于alpha濾波的LTV和ITV仿真算法，可以很好地表征短波信道信噪比秒量級(jí)和分鐘量級(jí)的變化，且將其集成于標(biāo)準(zhǔn)Watterson信道模型，可滿足當(dāng)前混合 ARQ數(shù)據(jù)鏈路協(xié)議等短波自適應(yīng)技術(shù)的試驗(yàn)需求，節(jié)省試驗(yàn)成本。

[1] 趙慧霞,許從方.短波自適應(yīng)跳頻技術(shù)的研究[J].通信技術(shù),2011,44(06)：7-9.

[2] 李丁山.基于 Watterson模型短波信道仿真算法[J].系統(tǒng)工程與電子技術(shù),2004,26(11)：1558-1560.

[3] 劉洋,朱立東.一種改進(jìn)的窄帶短波信道模型及仿真實(shí)現(xiàn)方法[J].通信技術(shù),2009,42(05)：1-4.

[4] STEWART F G.Technical Decription of ICEPAC Propagation Prediction Program [EO/OL].[2012-12-16].http：//www.voacap.com/itshfbc-help/icepac-techinro.html.

[5] FURMAN W N. Evaluation and Optimization of Data Link Protocols for HF Data Communications Systems[C]//IEEE MILCOM.Boston：MA,1993：67-72.

[6] BATTS W,FURMAN W N,KOSKI E. Channel Quality Variation as A Design Consideration for Wireless Data Link Protocols[C]//IEEE MILCOM. Orlando： FL,2007：1-10.