2次旋轉對稱布爾函數的兩個密碼學性質﹡

黃景廉， 王 卓

（西北民族大學 電氣工程學院，甘肅 蘭州 730030）

0 引言

布爾函數在密碼系統的設計中有著重要的應用，密碼系統的安全性取決于布爾函數的密碼學性質，如非線性度、代數次數、相關免疫性、擴散性、線性結構、平衡性、代數免疫性等[1-3]。對布爾函數密碼學性質的研究是序列密碼、分組密碼、Hash函數、數字簽名體制、數據加密技術的關鍵內容，其已成為密碼安全問題的一個重要研究領域。 2003年，法國密碼學家Nicolas和Wilimeier提出基于線性反饋移位寄存器的代數攻擊方法[4]。Courtois和Meier等學者隨之提出抵抗代數攻擊的布爾函數代數免疫性和代數免疫階 ()AI f的概念[4]。對布爾函數這一新性質的研究[5]更是當前密碼體制安全性研究的熱點。

旋轉對稱布爾函數是密碼學中已有良好實際應用的密碼學函數，用于某些密碼算法，如 MD4、MD5和HAVAL的快速實現中。在1999年由Pieprzyk和Qu提出[6]后一直受到重視，一直在對其進行深入研究[7-15]。文中將對旋轉對稱布爾函數、旋轉對稱H布爾函數的平衡性和代數免疫性展開研究，以得出一些有用的結果。

1 預備知識

定義1 設nI+∈，對任意(2)nGF,kI+∈,且,其中：

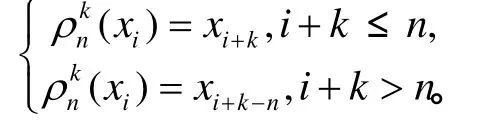
2次旋轉對稱H布爾函數已具有擴散性，在后面的討論中，還會涉及其它次數次的旋轉對稱布爾函數，故給出如下定義。

2 旋轉對稱布爾函數的性質

下面討論旋轉對稱布爾函數的一個性質。

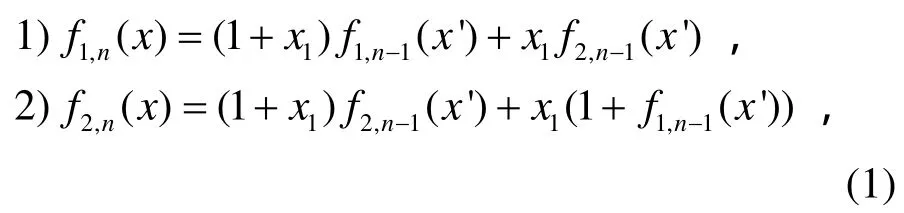
3) 在旋轉對稱布爾函數中，存在2次旋轉對稱平衡H布爾函數。

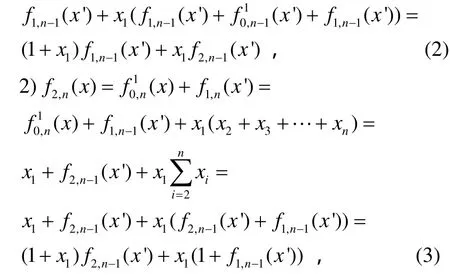
3) 由式(1)，便有：

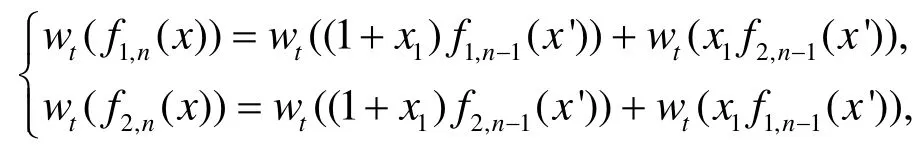
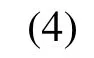
又有：

于是由式(4)、式(5)便可推得：

故由式(4)知，存在旋轉對稱平衡H布爾函數。

進一步還可推出：當 N1> N2，且，則必有只是這種隨維數的增大向 2n-1的逼近是很慢的，已無密碼學上的實際意義，不再以極限來描述。

推論2 奇數n維2次旋轉對稱H布爾函數中，存在平衡布爾函數；偶數n維2次旋轉對稱H布爾函數不是平衡布爾函數。

下面討論旋轉對稱布爾函數的代數免疫性。

i

(21)ik

+

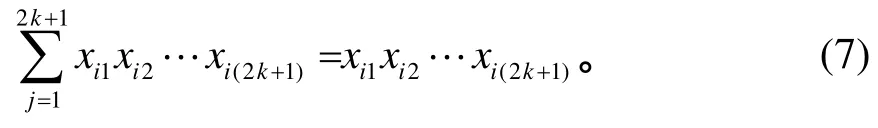
由式(7)、式(9)，便知有：

于是

2) 和1) 相似的道理，必有：

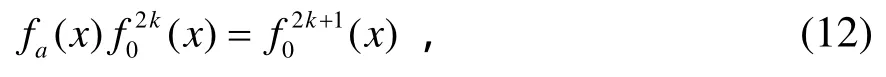
故

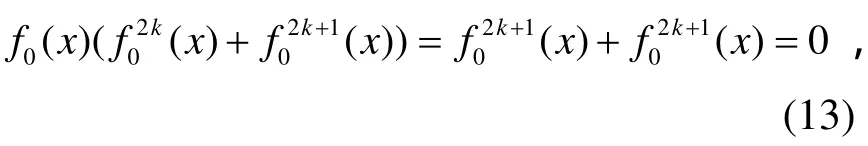
推論 3 若旋轉對稱布爾函數 ()f x只由完全純奇數次布爾函數的和構成，即

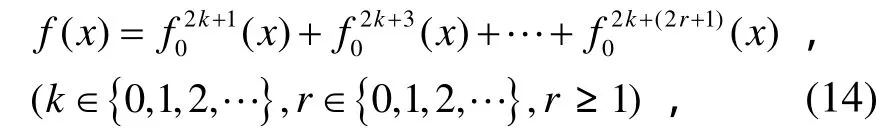
3 結語

文中給出了旋轉對稱布爾函數、完全純k次布爾函數的定義，討論了旋轉對稱布爾函數的性質，給出了相應的證明，得出 2次旋轉對稱布爾函數對平衡性的相容性、代數免疫階的結果，這些結果將為進一步深入研究旋轉對稱布爾函數、旋轉對稱H布爾函數的相關免疫性、代數免疫性、平衡性、重量分布范圍，平衡性、相關免疫性與維數的關系，以及多種密碼學性質的相容性等提供方便。

[1] 齊云,劉玉孝.相關免疫函數和Hamming重量之間的關系[J].通信技術,2008,41(12):363-365.

[2] 黃景廉,張椿玲.一次擴散布爾函數的一些密碼學性質[J].通信技術,2012,45(03):43-45.

[3] 蔡海,周亮.對AES算法的S盒布爾函數分析[J].信息安全與通信保密,2008(04):77-79.

[4] COURTOIS N, MEIER W. Algebraic Attacks on Stream Ciphers with Linear Feedback[C]//Eurocrypt 2003,Lecture Notes in Computer Science 2656. Berlin:Springer-Verlag,2003:345-359.

[5] 董新鋒,張鳳榮,譙通旭,等.具有最優代數免疫階的1階彈性函數的構造[J].信息安全與通信保密,2010(12):112-115.

[6] PIEPRZYK J,QU C.Fast Hashing and Rotationsymmetric Functions[J].Journal of Universal Computer Science,1999,5(01):20-31.

[7] CUSICK W,STANICA P,MAITRA S.Fast Evaluation,Weight and Nonlinearity of Rotation Symmetric Functions[J].Discrete mathematics,2002,258(1-3):289-301.

[8] STANICA P,MAITRA S.Rotation Symmetric Boolean Functions-count and Cryptographic Properties[J].Discrete Applied Mathematics, 2008(156):1567-1580.

[9] STANICA P,MAITRA S.Construction of Rotation Symmetric Boolean Functions with Optimal Algebraic Immunity[J]. Computer Systems, 2009, 12(03):267-284.

[10] 張鵬,付紹靜,屈龍江,等.平衡旋轉對稱布爾函數的計數[J].應用科學學報,2012,30(01):45-51.

[11] FU S,QU L,LI C,et al.Balanced Rotation Symmetric Boolean Functions with Maximum Algebraic Immunity[J].Information Security,IET, 2011, 5(02):93-99.

[12] 袁書宏,厲曉華,鄒池佳.關于旋轉對稱布爾函數性質之研究[J].浙江大學學報,2011,38(01):55-57.

[13] 熊曉雯,魏愛國,張智軍.構造具有良好密碼學性質的旋轉對稱布爾函數[J].電子與信息學報,2011,38(01):55-57.

[14] 王斌,張習勇,陳衛紅.一類4次旋轉對稱布爾函數的漢明重量和非線性度[J].數學學報,2012,55(04):55-57.[15] 董德帥,李超,屈龍江,等.偶變元MAI旋轉對稱布爾函數[J].國防科技大學學報,2012,34(04):85-89.