基于混合核的支持向量機數字預失真算法﹡

宋 勇， 胡 波， 李在清

（①上海貝爾股份有限公司，上海 201206；②復旦大學電子工程系，上海 200433）

0 引言

隨著現代通信系統對頻譜資源的需求日益增加，頻率效率更高的非恒包絡調制方式逐漸取代了原有的恒包絡調制方式。但是非恒包絡調制方式受功率放大器的非線性效應的影響較大，會產生帶內的失真和帶外的譜擴散，從而降低頻譜效率。因此提高功率放大器的線性度已經成為無線通信系統的一個很有挑戰性的問題。

預失真技術是目前應用最廣的線性化技術，以它的高效、穩定、自適應等優勢成為了目前的研究熱點[1-2]。目前使用較多的數字預失真算法采用基于維納濾波的線性濾波器為基礎的多項式模型，主要包括LMS、RLS、KF等算法[3]。支持向量機(SVM,Support Vector Machine)是在Vapnik等人建立的統計學習理論基礎上所發展起來的一種新的機器學習算法[4]，在處理非線性變換方面具有良好性能，已經被廣泛應用到模式識別和回歸分析等問題中[5]。

核函數的選擇是支持向量機中非常重要的一個環節。文中主要針對功率放大器的非線性特征，相應結合了兩種核函數的優點，構造了新型的混合核函數，并運用于數字預失真器中，取得了更好的性能。

1 系統模型

圖 1中為采用間接學習法的預失真算法結構圖。xk為輸入信號，它經過預失真器后生成信號 uk，再通過功率放大器后，就獲得輸出信號 yk。理想情況下 yk是 xk的一個延遲并放大后的版本(記為，文中設G=1。在每次數據流的循環中，SVM算法利用功率放大器的輸入 uk和輸出 yk，更新一次預失真函數f并用于下一數據流的預失真器中。

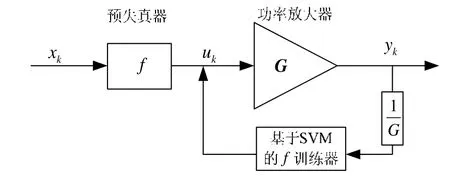
圖1 基于間接學習的預失真算法結構

2 基于SVM的預失真器

2.1 基于支持向量機的預失真器模型

支持向量機是一種基于結構風險最小化的統計學習方式[6]，它可以最終歸結為一個標準二次規劃問題，具有全局最優的特性。

在圖1的預失真算法結構圖中，預失真函數形式如式(2)，其中及b相當于未知的預失真系數，記憶深度為M。利用圖1中的模型進行f的學習。訓練開始時，SVM預失真器是直通的，因此以為輸出信號，通過SVM對f進行訓練。訓練過程可歸結為如下的帶約束QP問題：為輸入信號

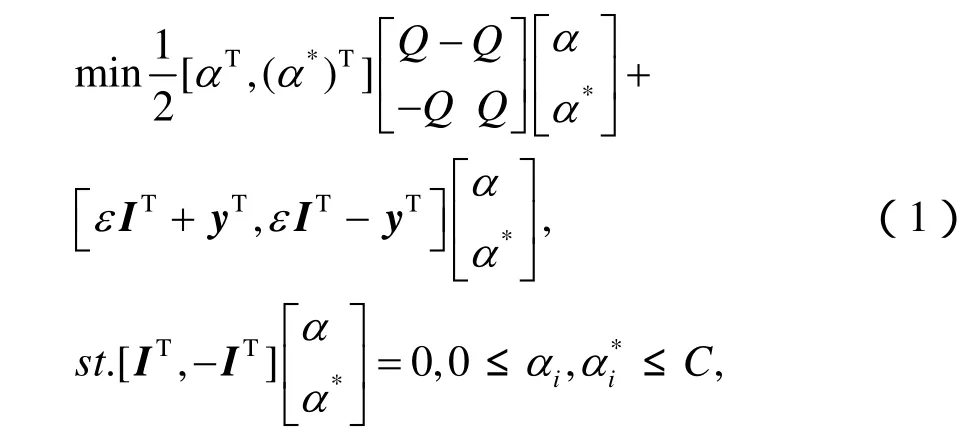
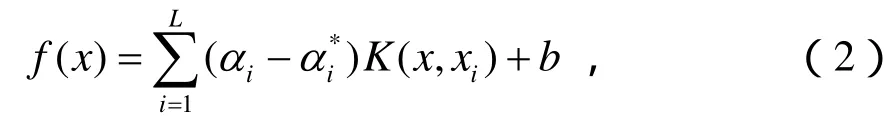
式中，b按下列方式計算：選擇位于開區間(0,)C中的jα或，

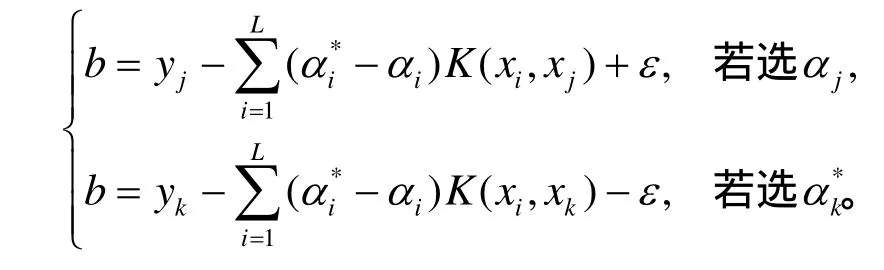
2.2 混合核函數

每種核函數有它們各自的特點，對SVM的回歸算法有著不同的影響。SVM的核函數分為全局核函數與局部核函數兩類。核函數的性能由學習能力和泛化能力共同決定。

SVM中常用的一個全局核函數是多項式核函數：

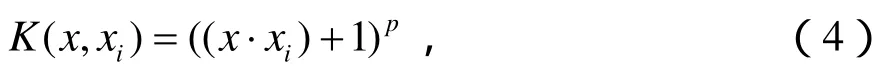
式中，pN∈，多項式核具有較好泛化能力，相距較遠的數據也能影響核函數的數值。

傅立葉核是文中主要用到的一種局部核函數：

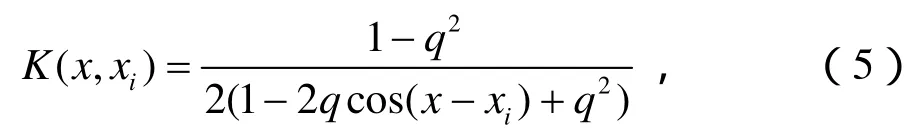
式中，q是滿足01q＜＜的常數。對傅立葉核僅測試點附近的數據點對其有影響，有較好的學習能力，但泛化能力較差。

因此，為了建立一個既有較好學習能力又有較好泛化能力的學習模型，可以充分利用以上兩類核函數的各自優點，將其進行組合，因此文中提出了如下的新型混合核函數：

式中，01ρ＜＜。ρ取值0和1時，混合核函數退化為傅立葉核函數和多項式核函數，其余取值下的核函數，其全局性和局部性均介于傅立葉核函數和多項式核函數之間。

3 仿真與分析

為了驗證文中預失真算法的有效性，利用Matlab進行了仿真驗證。仿真的輸入信號采用帶寬為20M的4載波WCDMA信號，采樣率為122.88 MHz。

預失真器采用式(2)的模型，樣本數L=200，式(1)中結構風險的參數C、ε和式(6)中混合核函數的參數p、q、ρ均由交叉驗證法獲得最優值，此處分別取值為C=1.58，ε=1e-5，p=3，q=0.67，ρ=0.999。

功率放大器采用Wiener模型，其線性動態子系統的記憶長度為2：

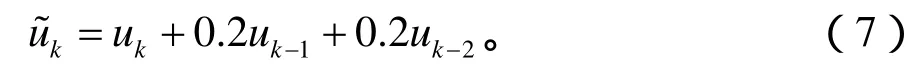
無記憶非線性子系統的階數為5：

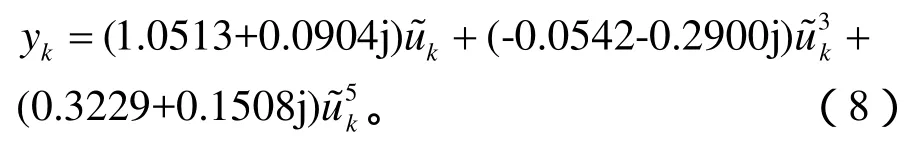
文中的混合核函數中局部核函數是取用的傅立葉核函數，而徑向基核函數也是較常用的局部核函數[7]，為了驗證提出的算法的性能，將文中的混合核函數(P-F-SVM，Polynomial-Fourier SVM)算法與多項式-徑向基混合核函數(P-R-SVM，Polynomial-RBF SVM)算法以及傅立葉核函數(F-SVM，Fourier SVM)算法的性能進行了比較。上述核函數中的變量p，q，ρ都已通過交叉驗證法取得最優值。

基于LMS的DPD算法是一種廣為研究的DPD算法[8]。為了衡量文中提出的DPD算法的性能，與其進行了性能比較。其中基于LMS的DPD算法采用的輸入數據長度為10 000，迭代步長0.1μ=，并取0.5ε=。

圖2給出了基于SVM的幾種DPD算法和基于LMS的DPD算法的預失真前后的功率譜密度曲線。從圖2中可以看出文中提出的P-F-SVM DPD算法的性能是最優的，優于P-R-SVM DPD和F-SVM DPD兩種基于SVM的算法的曲線，也優于基于LMS 的DPD算法曲線，對功率放大器的非線性失真以及記憶失真進行了較好的校正。

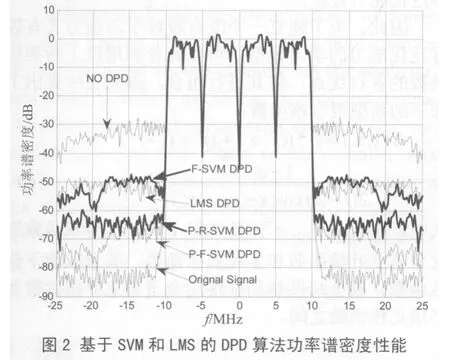
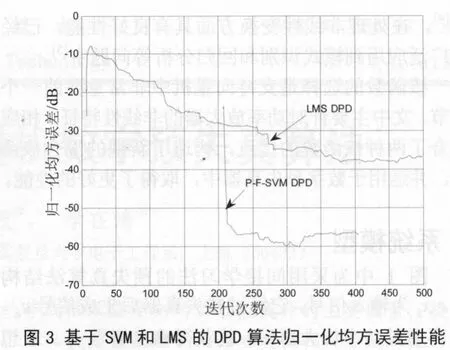
圖3中比較了文中提出的基于SVM的算法與基于 LMS的 DPD算法的歸一化均方誤差(NMSE，Normalized Mean Square Error)收斂曲線，其中圖3中的迭代曲線里，P-F-SVM DPD算法的曲線從200以后開始計算，因為它前面的200個點用來生產樣本點。從圖3中可以看出，P-F-SVM DPD算法的收斂速度比基于 LMS的DPD算法快,而且在迭代收斂后,P-F-SVM DPD算法的平均NMSE性能要比基于LMS的DPD算法高18 dB。

4 結語

文中介紹了SVM算法進行非線性回歸的原理，提出了一種基于SVM的DPD算法。通過構造基于傅立葉核函數和多項式核函數的混合核函數，得到了既有較好學習能力又有較好泛化能力的模型。在文中仿真條件下，性能優于基于其它核函數的SVM DPD算法，且與基于LMS的DPD算法相比，文中算法的功率譜密度性能提高了12 dB，NMSE性能提高了18 dB，改善了算法性能，從而提高了功率放大器的線性度。

[1] 陳斌,任國春,龔玉萍.基于多項式與查找表的預失真技術研究[J].信息安全與通信保密, 2011(03):44-46.

[2] 王飛俊,金明錄,孫鵬.一種數字預失真器的實現方法[J].通信技術,2011,44(01):154-156.

[3] 張志剛,林其偉,韓霜,等.OFDM系統自適應數字預失真研究[J].通信技術,2011,44(04):50-52.

[4] VAPNIK V.An Overview of Statistical Learning Theory[J].IEEE Transactions on Neural Network,1999,10(05):988-999.

[5] ADANKON M M,CHERIET M,BIEM A.Semisupervised Learning Using Bayesian Interpretation:Application to LS-SVM[J].IEEE Transactions on Neural Networks,2011,22(04):513-524.

[6] CRISTIANINI N,SHAWE-TAYLOR J.An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods[M].Cambridge:Cambridge University Press, 2000: 47-98.

[7] ZHAO Z D,LOU Y Y,NI J H.RBF-SVM and Its Application on Reliability Evaluation of Electric Power System Communication Network[C].International Conference on Machine Learning and Cybernetics, Baoding: IEEE,2009(02):1188-1193.

[8] LI B,GE J,AI B.Robust Power Amplifier Predistorter by Using Memory Polynomials[J].Journal of Systems Engineering and Electronics,2009,20(04):700-705.