數據驅動隨機子空間法矩陣維數選擇與噪聲問題研究

辛峻峰，盛進路，張永波

(1.中國海洋大學 工程學院，青島 266100;2.大連海事大學 航海學院，大連 116026;3.青島國家海洋科學研究中心，青島 266071)

有效的模態識別方法能精確地得到結構的相關參數，從而可以準確地掌握大型結構的健康狀況。國內外許多學者［1-3］提出了基于時域響應的模態參數識別方法，如時間序列法、隨機減量法、自然激勵技術、數據驅動隨機子空間法等。其中，數據驅動隨機子空間法是目前為止較為先進的環境激勵下模態參數識別方法之一，它能夠更精確地提取海洋平臺等大型結構的模態參數。但是，確定Hankel矩陣的維數是該方法有效應用的關鍵［4］，不同的Hankel矩陣維數會導致數據驅動隨機子空間法消噪能力的變化。如何確定Hankel矩陣的維數?目前對這個問題的研究還鮮見報道。針對于此，本文推導了Hankel矩陣的維數與數據驅動隨機子空間法消噪能力的理論關系，繼而提出了數據驅動隨機子空間法Hankel矩陣維數的選擇方法，探討了不同的Hankel矩陣構建方式與數據驅動隨機子空間法消噪能力的關系。

1 數學理論

1.1 數據驅動隨機子空間識別法

在僅考慮隨機噪聲的前提下，振動系統的離散狀態空間方程可表示為:

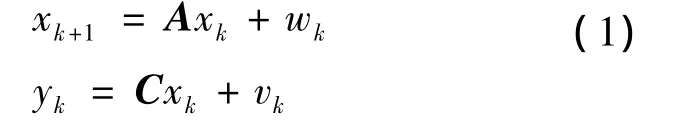
其中:xk∈Rn表示在離散時間k時，系統的狀態向量，n為系統的階數;A∈Rn×n表示離散狀態矩陣;C∈Rl×n表示輸出矩陣，描述內部狀態怎樣轉化為外界測量值，l表示測點的數目;wk∈Rn表示由于干擾和模型誤差造成的過程噪聲;vk∈Rl表示由于傳感器誤差等造成的測量噪聲。這兩種噪聲都是不可測量的，在推導過程中經常被假設為零均值，平穩的白噪聲。兩種噪聲的協方差矩陣可以用下式表示:

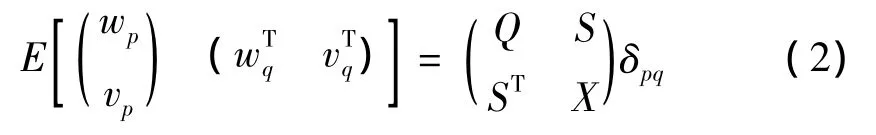
其中:E表示數學期望算子;Q∈Rn×n，S∈Rn×l，X∈Rl×l;δpq為 Kronecker函數，δpq=1(p=q)，p和q表示不同的時間點，δpq=0(p≠q);E［wp］=0，E［vp］=0。

數據驅動隨機子空間識別法詳細討論可見文獻［5-7］。

1.2 Hankel矩陣維數選擇與噪聲關系

通常數據驅動隨機子空間法的投影矩陣P可以進一步表示成如下:

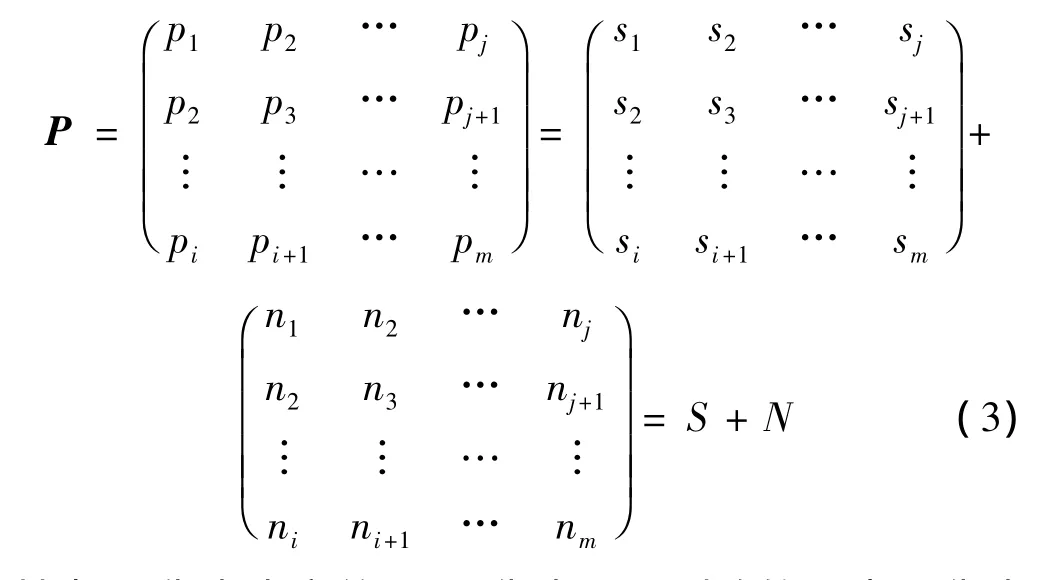
其中:S代表真實信號;N代表需要剔除的噪聲;i代表Hankel矩陣1/2行數;j代表矩陣列數;m代表數據總量。

繼而在奇異值分解(SVD)后，設定閾值(模態階次)n，式(3)變為:

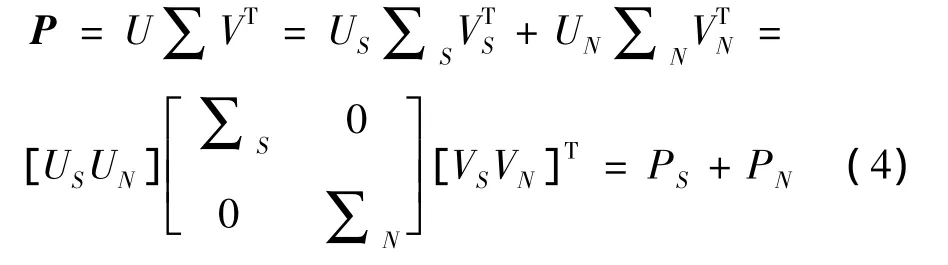
其中:PS=US∑S，PN=UN∑N，U∈Ri×i，∑∈Ri×j，V∈Rj×j，∑代表分解后測量信號投影后包含的所有奇異值;∑S代表設定閾值n后，真實信號投影后包含的奇異值。∑N代表設定閾值n后，噪聲信號投影后包含的奇異值。由式(4)可得，奇異值分解可以將含噪聲的投影矩陣P劃分為兩個互不相關的空間，即真實信號投影PS和噪聲信號投影PN。下面討論式(4)中噪聲投影PN與所有測量信號投影P的維數(行數i或者列數j)及其奇異值分解閾值n兩個參數之間的關系。

根據式(4)有:

由于真實信號與噪聲不相關，所以:

由式(5)及式(6)可得:

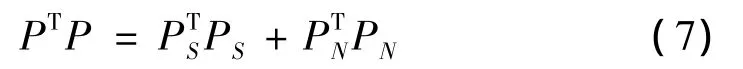
因為測量信號、真實信號以及噪聲的投影的協方差分別為:

式(7)可改寫為:

結合式(4)與式(8)，式(9)可以寫為:

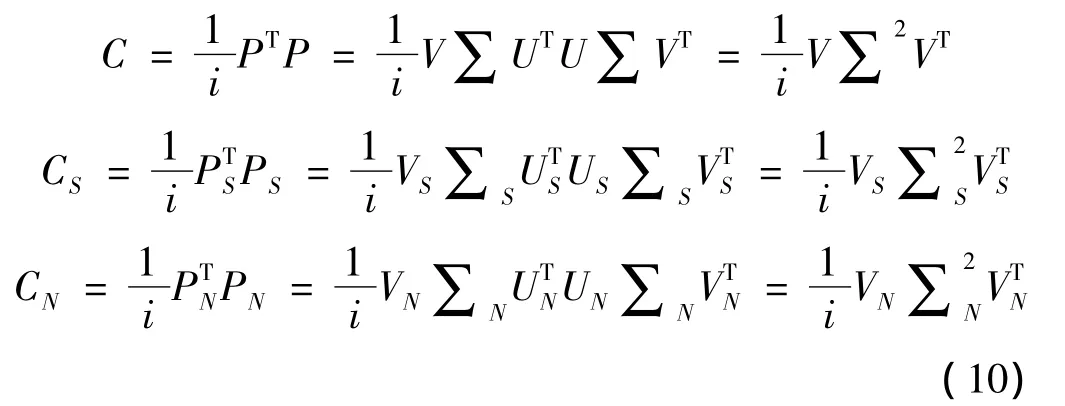
由式(8)到式(10)可得:

式(11)左右兩邊同時左乘iVT和右乘V得:

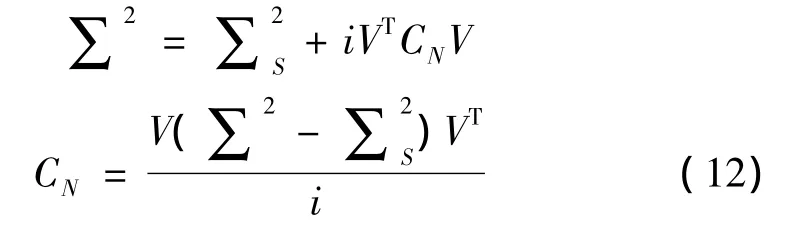
式(12)中，在數據總量m不變的前提下，V與∑S取決于Hankel矩陣維數(行數2i或者矩陣列數j，2i+j-1=m)和投影矩陣奇異值分解的閾值n，∑取決于Hankel矩陣維數(行數2i或者矩陣列數j，2i+j-1=m)。所以，如果投影奇異值分解的閾值n不變，Hankel矩陣的維數是影響噪聲CN的主要因素。

1.3 穩定圖

本文的穩定圖采用了信號的傅里葉變換作為背景，顯示了模態階數在0到30 Hz之間模態識別結果的情況。對于同一模態，如果前后兩次識別結果同一模態的模態頻率誤差在1%，同時響應阻尼的識別結果的誤差在5%，即，

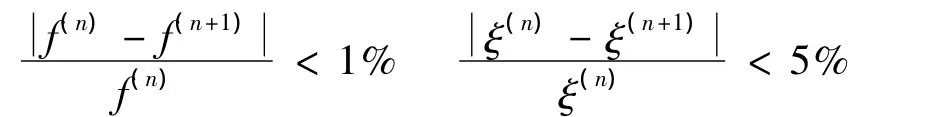
則此次識別的結果標識為穩定，否則為不穩定［8］。

2 數據驅動隨機子空間法－矩陣維數設定評估方法

歸一化奇異值(SVD)、穩定圖以及有限元模態識別結果(FE)三維一體評估方法。操作流程和每一步的功能性如圖1所示。

3 Hankel矩陣構建方案

設數據總量為m(2i+j-1=m)，分別對四種Han-kel矩陣維數設定方案(2i/m=2/10，3/10，4/10，5/10)進行探討，其中，方案一(2i/m=2/10)，表示 Hankel矩陣 H是一個較扁平的非方陣;而方案四(2i/m=5/10)，表示Hankel矩陣H是一個方陣，因此方案一到方案四的變化過程也是Hankel矩陣從一個扁平的非方陣逐漸變為方陣的過程。

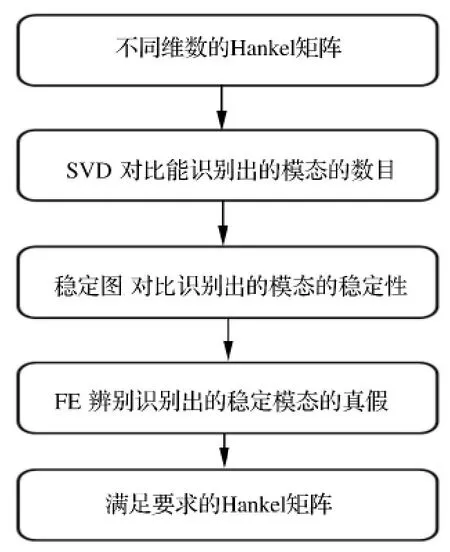
圖1 評估方法操作流Fig.1 Operation process of evaluation method

4 數值算例

本節將通過五自由度質量-彈簧-阻尼系統白噪聲激勵試驗(模型如圖2所示)，探討不同Hankel矩陣的維數對數據驅動隨機子空間法消噪能力的影響，同時驗證SVD、穩定圖、FE組合評估方法的有效性。

4.1 五自由度質量－彈簧－阻尼系統

每個單元有相同的質量、剛度和阻尼系數，分別被設定為:mn=50 kg，kn=2.9 ×107N/m，cn=1 000 Ns/m。xn代表位移，并且n=1，…，5。通過特征值分析，得到 5階模態頻率的理論值為:34.499、100.700、158.730、203.880、232.520 Hz;5 階模態阻尼比的理論值為:0.003 737、0.010 909、0.017 197、0.022 092、0.025 198［8-9］。

圖2 自由度彈簧-質量-阻尼系統Fig.2 A 5-DOF mass-spring-dashpot system

4.2 白噪聲激勵加載及數據獲取

采用Matlab中randn函數生成均值為零，標準差為1.006的高斯白噪聲作為輸入(圖3)將其右向加載在靠固定端的第一個質量塊上(圖2)，從lsim函數生成振動響應，以500 Hz的采樣頻率提取第一個質量塊的1 024個響應數據，如圖4所示。

4.3 不同方案對比

首先使用歸一化奇異值對比不同方案能識別出的模態的數目。

圖3 輸入的白噪聲序列Fig.3 White noise loading

圖4 靠固定端質量塊響應Fig.4 Response of mass close to fixed point

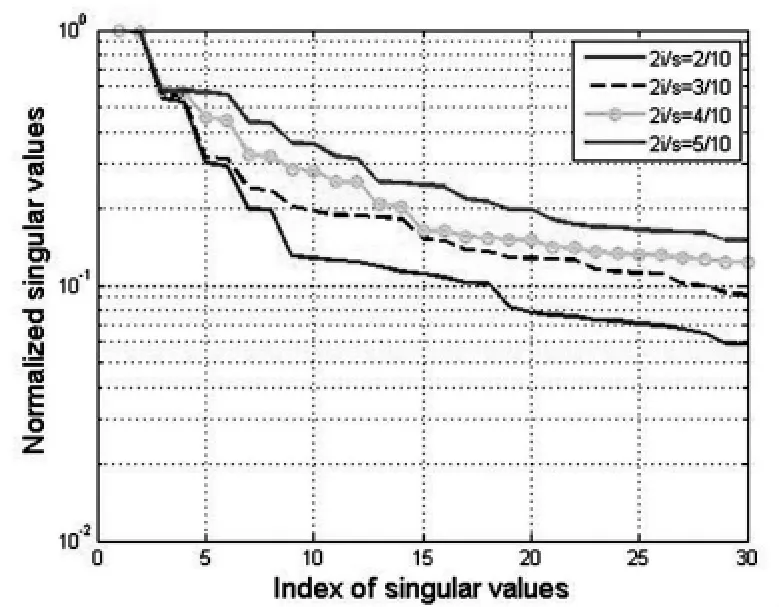
圖5 四種方案歸一化奇異值曲線Fig.5 Normalized singular values in four cases

歸一化奇異值的結果(圖5)清晰地顯示出:當Hankel矩陣從扁平(方案一，2i/m=2/10)趨于方陣(方案四，2i/m=5/10)的過程中，數據驅動隨機子空間法能清晰識別的模態數目從4個(方案一，紅線最后的較大落差在橫軸為8的時候)減少到1個(方案四，紫色線最后的較大落差在橫軸為2的時候)。這說明Hankel矩陣趨于方陣的過程中，數據驅動隨機子空間法的消噪能力逐漸減弱，從而導致了其識別出的模態越來越少。

接下來，利用穩定圖分析結果對比不同方案下識別出的模態的穩定性，如圖6所示。

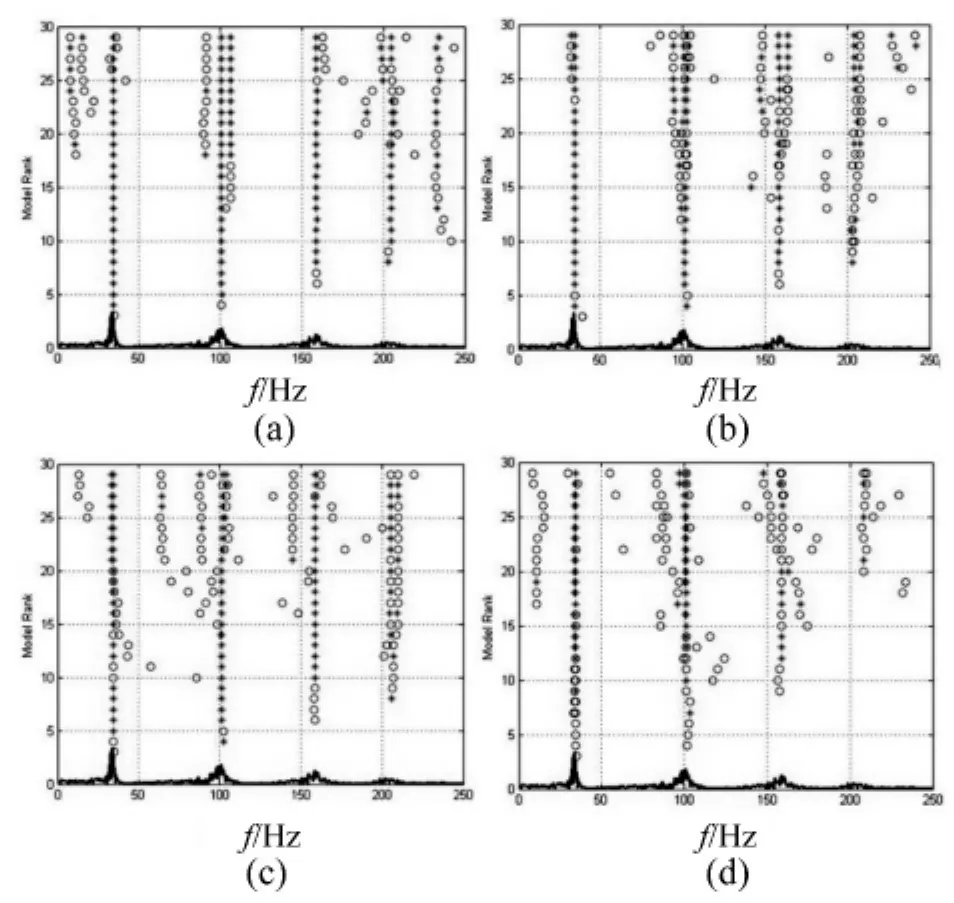
圖6 SSI/data四種方案的穩定圖分析結果(a)～(d)對應著方案一，2i/m=2/10到方案四2i/m=5/10，代表穩定，o代表不穩定)Fig.6 Stability Diagrams for SSI-data in four cases(a-d responding to case 1，2i/m=2/10 to case 4，2i/m=5/10，*stable，°not stable)

穩定圖清晰地顯示了在Hankel矩陣趨于方陣的過程中(圖6，(a)-(d)):

(1)數據驅動隨機子空間法逐漸地不能穩定識別出區間在200 Hz左右的第四階模態和區間在230 Hz左右的第五階模態(代表不穩定的圓圈逐漸增多;對應峰值的直線逐漸消失或者發生混亂)，這個現象說明數據驅動隨機子空間法消噪能力在逐漸減弱，從而導致其對弱一些的模態越來越不敏感。

(2)數據驅動隨機子空間法對最強的兩個模態(區間分別在30 Hz和100 Hz左右的第一階模態和第二階模態峰值最大)的估計逐漸變的不穩定(代表不穩定的圓圈逐漸替代代表穩定的星號)，這證明了數據驅動隨機子空間法的消噪能力在逐步減弱，從而導致了其對較強模態的識別也減弱了。

表1 SSI/data四種方案下的模態頻率估計結果Tab.1 Frequencies estimated in four cases using

最終，通過參考有限元的模態分析結果(FE)，確定不同方案識別出的穩定模態的真假。表1和表2分別羅列了不同方案估計的模態頻率和阻尼比。

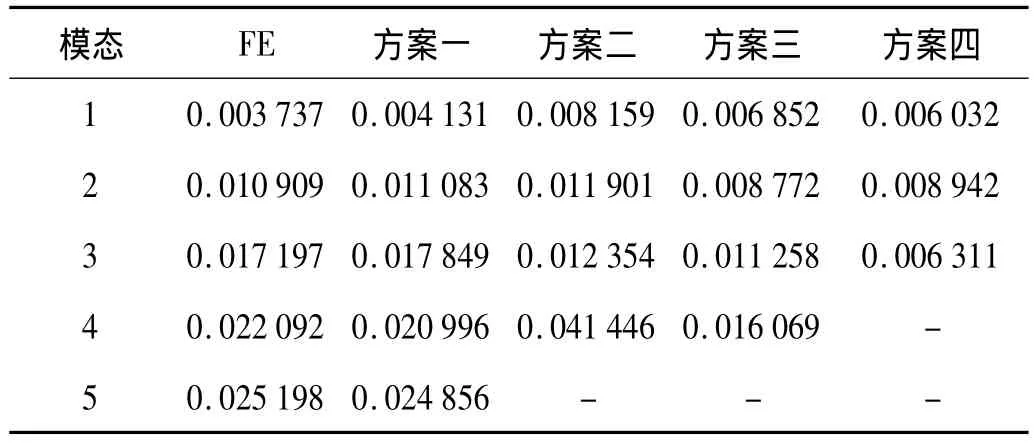
表2 SSI/data四種方案下的模態阻尼比估計結果Tab.2 Damping ratios estimated in four cases using

表1和表2，不但確定了方案一識別出的5個模態的真實性，而且能夠觀察到:Hankel矩陣從方陣(方案四)趨于非方陣(方案一)的過程中，數據驅動隨機子空間法對模態參數的估計逐漸精確，尤其是對模態阻尼比的估計。

此外，本文分別使用了含有不同噪聲水平的響應數據，進行分析得到的結論與上文一致。

總之，數值算例證明了:① 數據驅動隨機子空間法的Hankel矩陣應該設置成非方陣的形式;② SVD、穩定圖以及FE相結合的方法能夠有效評估不同Hankel矩陣維數對數據驅動隨機子空間法模態識別能力的影響。

5 導管架平臺振動臺試驗

本節將進行鋼導管架平臺物理模型白噪聲激勵試驗進一步驗證上文的研究結論。試驗方案為:使用液壓振動臺產生白噪聲激勵，在鋼導管架平臺物理模型底部加載(與x軸和y軸成45度角)，獲得結構的振動響應數據，繼而對比不同方案下的數據驅動隨機子空間法的消噪能力。

5.1 導管架平臺物理模型及試驗

本導管架物理模型采用鋼管制作，在Y向設3根主梁，X向設2根，有3層水平橫撐，分別位于-88 cm、142 cm和188 cm處設水平橫撐，在88 cm至-142 cm處設豎向斜撐(圖7)，主要構件的尺寸為:主腿25×2.5 mm，水平撐桿 16 ×1.5 mm，斜撐桿 16 ×1.5 mm［10］。

鋼導管架平臺有限元模型的前9階模態如表3所示。

用液壓振動臺生成白噪聲激勵，如圖8所示。以500 Hz的采樣頻率，在y方向的傳感器A提取了1 024個數據點(圖8)。

圖7 導管架平臺物理模型，白噪聲激勵加載位置以及傳感器位置Fig7.Physical model of jacket platform，white noise ground motion loading position and the sensor A location

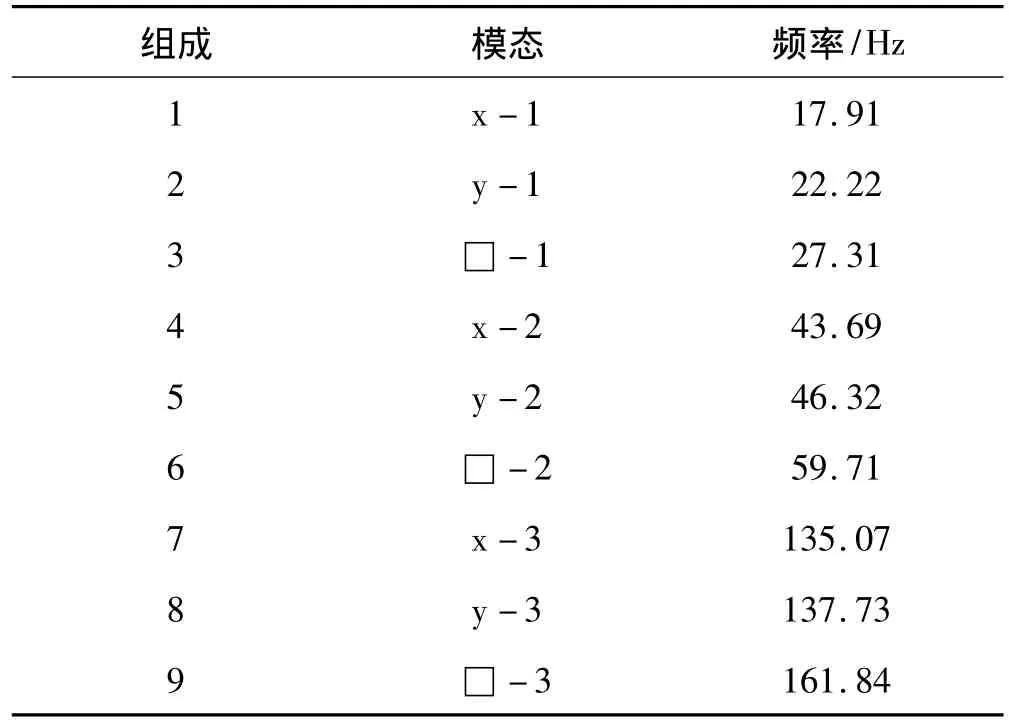
表3 有限元模型前9階模態頻率Tab.3 The first nine modal frequencies of FE

圖8 白噪聲激勵傳感器A的響應信號Fig.8 Response of sensor A from white noise ground motion

5.2 不同方案對比

跟數值算例中的分析過程一致，首先用歸一化奇異值對比不同方案。

歸一化奇異值(圖9)清晰地顯示出:當Hankel矩陣H趨于方陣的過程中，數據驅動隨機子空間法能識別出的模態數目不斷增加。從4個(方案一(2i/m=2/10)，紅線最終較大落差在橫軸為8的時候)逐漸增加到6個(方案四(2i/m=5/10)，紫色線最終較大落差在橫軸為12的時候)。這結果似乎在表明方陣的Hankel矩陣使數據驅動隨機子空間法識別更多的模態，為了證實這一點，下文結合穩定圖繼續分析。

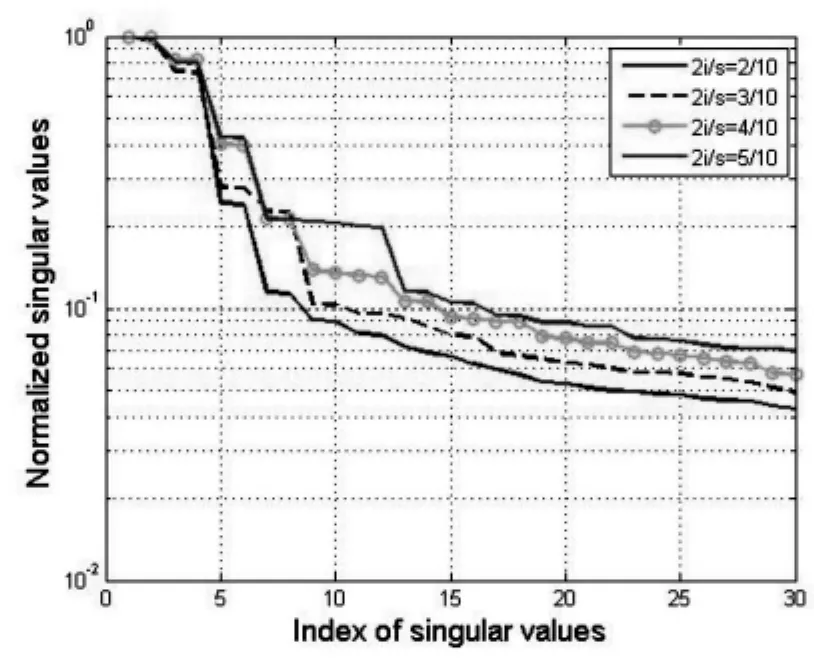
圖9 導管架試驗，SSI/data四種方案歸一化奇異值曲線Fig.9 Normalized singular values in four cases in jacket platform model test

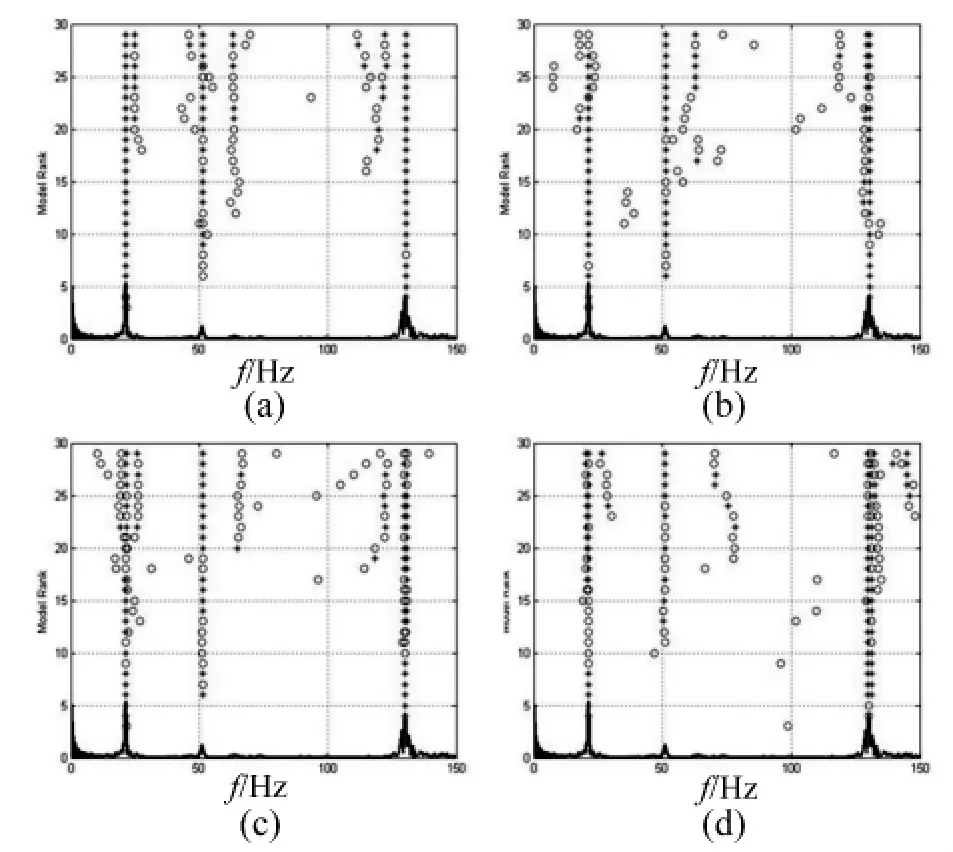
圖10 導管架試驗，SSI/data四種方案的穩定圖分析結果(圖a-d對應著2i/s=2/10到2i/s=5/10，*代表穩定，o代表不穩定)Fig.10 Stability Diagrams for SSI-data in four cases in jacket platform model test.(a-d responding to case 1，2i/s=2/10 to case 4，2i/s=5/10，*stable，°not stable)

伴隨著Hankel矩陣趨于方陣(圖10，a到d)，從穩定圖中可以觀察到:

(1)在30 Hz、50 Hz、130 Hz三個最大的峰值處，數據驅動隨機子空間法的識別結果越來越不穩定(代表不穩定的圓圈逐漸增多。

(2)方案一(2i/m=2/10，圖10(a))與方案二(2i/m=3/10，圖10(b))都能穩定地識別出4個模態，比其他方案識別的模態多，但是它們在第四階模態的識別上有所不同:方案一識別出的第四階模態在60 Hz左右，而方案二在130 Hz左右。

(3)只有方案一(2i/m=2/10，圖10(a))與方案二(2i/m=3/10，圖10(b))穩定圖的分析結果與歸一化奇異值分析一致:能識別出4個模態，這個現象表明本文提出的評估方法的第二步(穩定圖分析)的必要性。

在穩定圖的分析中，方案一與方案二的識別出的模態較多，但是在第四階的模態識別上出現了不一致。由此，需要FE作為參考來辨別識別出的模態的真假。表4和5中羅列了不同方案的評估結果(模態階數為20)。

表4 SSI/data四種方案下的模態頻率估計結果Tab.4 Frequencies estimated in four cases using SSI/data

表5 SSI/data四種方案下的模態阻尼比估計結果Tab.5 Damping ratios estimated in four cases using SSI/data

在表4和5中，參照FE的結果，可以觀察到:

(1)第四階模態應該是在63 Hz左右的扭轉模態，方案一(2i/m=2/10)的識別結果是正確的。

(2)只有方案一(2i/m=2/10)能識別出63 Hz左右的第四階模態，證明了方案一的優勢，這個結果表明了本文提出的評估方法第三步(FE驗證)的必要性。

總之，導管架平臺白噪聲試驗與數值試驗的分析結果一致:本文提出的評估方法有效而且非方陣的Hankel矩陣使數據驅動隨機子空間法具備更強的消噪能力和更高的模態識別精度。

6 結論

本文利用SVD、穩定圖和FE相結合的方式對數據驅動隨機子空間法的Hankel矩陣維數進行選擇。其中，首先用SVD對比不同Hankel矩陣下數據驅動隨機子空間法能識別出的模態數目，篩選出能識別較多模態的Hankel矩陣;繼而使用穩定圖對比模態的穩定性，進一步篩選出穩定模態最多的Hankel矩陣;最后參考FE的結果辨別穩定模態的真假，再進一步篩選出真模態最多的Hankel矩陣。基于此方法，通過數值分析和導管架平臺振動臺試驗，探討了數據驅動隨機子空間法的Hankel矩陣維數與其消噪能力之間的關系。系統地證明了:為了最大程度地提高數據驅動隨機子空間法的消噪能力和對弱模態的敏感度，Hankel矩陣應采用非方陣的形式(即行數大于列數)。本文的工作可為今后數據驅動隨機子空間法的有效推廣和應用提供參考。

［1］Wang S Q. Comparativestudyofoutput-based modal identification methods using measured signal from an offshore platform，Proceedings ofthe ASME 29th International Conference on Ocean［C］. Offshore and Arctic Engineering，2010.

［2］ Hu S L J，Li P，Vincent H，et al.Modal parameter estimation for jacket-type platforms using free-vibration data［J］. Journal of Waterway， Port， Coastal， and Ocean Engineering，2011:1943-1963.

［3］ Cunha A，Caetano E.Experimental modal analysis of civil engineering structures［J］.Sound and Vibration，2006:12-20.

［4］劉進明，應懷樵，沈 松，等.時域模態分析方法的研究及軟件研發［J］.振動與沖擊，2004，23(4):123-126.

LIU Jin-ming，YING Huai-jiao，SHEN Song，et al.Method research and software developing of time domain modal analysis［J］.Journal of Vibration and Shock，2004，23(4):123-126.

［5］ Overschee P，DeMoor B.Subspace identification for linear system:theory-implementation-applications［M］.Kluwer Academic Publishers Boston/London/Dordrecht，1996.

［6］ Peeters B，DeRoeck G.Stochastic system identification for operational modal analysis:A review［J］.Journal of Dynamic Systems，Measurement，and Control，2001，123:659-667.

［7］Peeters B，DeRoeck G.Reference-based stochastic subspace identification for output-only modal analysis［J］.Mechanical Systems and Signal Processing，1999，13(6):855-878.

［8］ Hu S L J，Bao X，Li H.Model order determination and noise removal for modal parameter estimation［J］.Mechanical Systems and Signal Processing，2010，24:1605-1620.

［9］ The MathWorks，Control system toolbox user’s guide，The MathWorks Inc.，Natic，MA，2004.

［10］ ANSYS.Inc，ed.，2004.ANSYS Academic Research.Release 9.0.Help System.Coupled Field Analysis Guide10.