基于響應面法的結構動力學模型修正

鮑 諾，王春潔，趙軍鵬，宋順廣

(1.北京航空航天大學 虛擬現實技術與系統國家重點實驗室，北京 100191;2.北京航空航天大學 機械工程及自動化學院，北京 100191)

精確的動力學模型對于結構的動力學特性預測及設計具有重要意義。由于結構的復雜性，在分析過程中存在眾多的不確定因素以及建模中的簡化，如材料參數誤差，邊界條件誤差，結構連接參數誤差，局部或整體的非線性等，導致有限元模型計算結果與實際結構的動力學特性之間必然存在誤差［1-2］。為減少因模型參數不確定而造成結構動力學數值模擬的偏差，利用試驗數據對初始有限元模型進行修正，以便準確的預示結構動力學行為。

響應面法具有易于迭代和優化的特點，近年來在結構優化設計等工程領域得以應用。Heinonen等［3］用不同函數的響應面法對板狀結構在滿足約束條件下進行質量最小優化，分析結果驗證了方法的可行性。Alaswad等［4］用有限元和RSM相結合的方法對管件液壓成型進行分析，算例表明該方法可以用來預測管件液壓成型。姜衡等［5］利用二次多項式響應面對立式加工中心實現了動靜態多目標優化，該方法具有較高的精度和工程實用性。杜家政等［6］利用響應面法對五心底結構形狀優化設計，證實了算法的有效性。

針對模型結構參數的修正過程中迭代困難且有限元軟件中難以引入新型優化算法的問題。本文提出了響應面和和優化算法相結合的思想進行有限元模型修正，利用響應面來替代有限元模型結合新型優化算法進行優化，避免迭代過程每次調用有限元程序，提高了修正效率和精度。以歐洲航空科技組織采用的基準模型GARTEUR飛機模型為算例，構建其響應面模型并優化修正參數，獲得修正模型。將測試頻段和預測頻段的模態頻率與實測數據相互對比，驗證了響應面和優化算法相結合的模型修正方法的有效性。

1 初始模型建立及修正流程

GARTEUR飛機模型由法國國家航空航天研究院設計制造，該模型能真實地模擬實際飛機的低剛度、高柔度、模態頻率低且密集的特點。目前，歐洲航空科技組織已將GARTEUR飛機模型用做評估動力學試驗與模型修正技術的標準模型，眾多國家的科研機構也用其來評估試驗分析技術及驗證數值計算［7-8］。

1.1 GARTEUR模型構建

GARTEUR飛機模型主要由截面為矩形的鋁制梁構成，包括機身、機翼、垂直尾翼、水平尾翼、兩邊小翼等部件，如圖1所示。其中機身長1.5 m，翼展2.0 m，機翼上表面附著一層粘彈性阻尼材料。

利用Patran軟件對GARTEUR飛機模型進行有限元建模，如圖2所示。機身、機翼、兩邊小翼、水平尾翼、垂直尾翼采用梁單元模擬。由于模型各個零部件采用螺栓、鉚釘連接，在所有連接處都相應增加集中質量單元模擬連接件質量。機翼連接處采用兩個對稱剛性單元，機身與機翼的連接為BUSH單元連接，垂直尾翼與機身連接為剛性單元。初始有限元模型中各剛性單元長度、偏置距離及剛度等參數都需要進一步根據試驗數據進行修正，以便獲得精確的動力學模型。

圖1 GARTEUR飛機結構Fig.1 Structure of GARTEUR benchmark

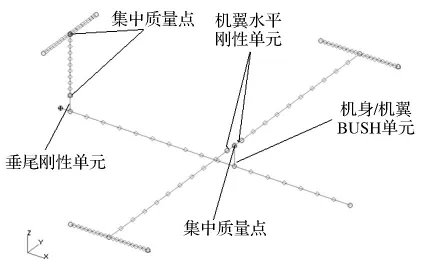
圖2 GARTEUR飛機有限元模型Fig.2 Finite element model of GARTEUR benchmark

初始模型中機身、機翼等部件的幾何和材料參數相對準確，但結構連接處的模型簡化較多、誤差較大。根據建模過程中連接結構的特點，對誤差集中的連接處的等效建模參數進行選擇修正。將建模過程中的機翼彎曲剛度和扭轉剛度、機身/機翼連接處扭轉剛度、機身彎曲剛度、垂直尾翼彎曲和扭轉剛度、兩邊小翼彎曲剛度、機翼對機身垂直偏置距離、各剛性單元長度等設計參數作為修正變量。具體模型修正參數，如表1所示。

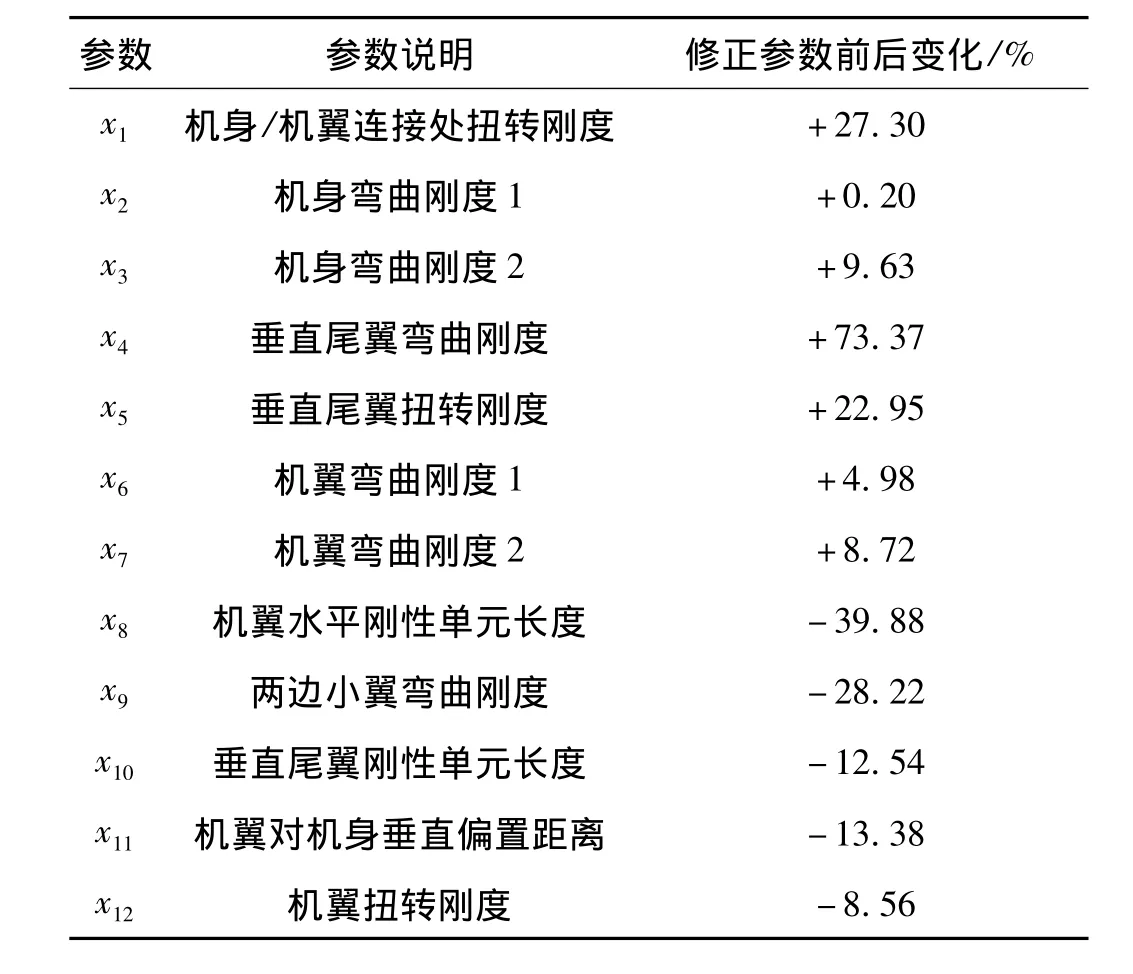
表1 模型修正參數及其修正變化量Tab.1 Model updating parameters and its changes

1.2 模塊化修正流程

考慮到模型多次迭代性，方便參數修正對建模誤差進行補償，建立精確的等效參數模型。采用PCL語言編寫模型分析程序，將初始有限元模型所選擇的修正變量參數化，建立起參數化模型。將基于響應面法的模型修正流程模塊化，如圖3所示。主要包括:①參數化模型模塊;② 響應面模塊;③ 優化模塊。具體流程是:首先對試驗設計的結果應用參數化模型模塊進行有限元分析，其次將分析數據構建成響應面，再次應用優化模塊對響應面進行優化，最終將參數優化的結果帶入到初始有限元模型中，將響應結果與試驗數據進行比較，驗證基于響應面法有限元模型修正的可行性。

2 基于試驗設計的響應面模型構建

圖3 基于響應面法的模型修正流程Fig 3 Flowchart of response surface-based model updating

基于試驗設計的響應面方法(RSM)是用統計方法對響應受多個變量影響的情況進行建模與分析。基本思想是在設計變量的連續參數區間內，以試驗設計方法獲取樣本點值，利用回歸分析技術，將特征量與設計變量的復雜隱式關系用顯式函數式近似表達出來，得到響應面模型。然后在響應面模型的基礎上進行迭代修正，避免每次迭代都調用有限元軟件分析，顯著提高計算效率。GARTEUR算例的有限元模型修正模塊化流程，如圖4所示。

圖4 GARTEUR模型修正流程圖Fig.4 Flowchart of GARTEUR model updating

2.1 樣本點選取

試驗設計是以概率統計為理論基礎，研究多因子與響應變量關系的一種科學方法。常見的試驗設計方法有全因子法、部分因子法、中心復合法、拉丁方法等［9］。構造的樣本試驗點在修正參數區間內的分布對響應面的近似精度有很大影響。

本文采用的優化拉丁方試驗設計法是在拉丁方試驗的基礎上增加一個準則［10-11］，求得此準則下最優的拉丁方(LHS)設計。因此，試驗設計矩陣每列中各個水平出現的次序和各個樣本點的因子水平分布更加均勻，抽樣效果好。在GARTEUR模型中12個修正變量各自不同的連續區間參數范圍內，采用優化拉丁方抽樣選取樣本點，并應用GARTEUR模型的參數化模塊求解抽樣點對應的結構頻率響應值。

2.2 響應面模型建立

采用精確度更高的不完全4階多項式作為響應面近似函數，將多組采樣點及其對應的響應值運用回歸、擬合、差值方法創建響應面模型，通過模型檢驗來驗證響應面模型是否可信。從而構造出具有明確表達形式的顯式函數代替原結構進行建模和分析。不完全4階響應面近似函數構造形式為:

由試驗設計確定的樣本點組成設計變量矩陣X，通過有限元分析可得有限元模型計算值向量Y;假定有限元計算值與響應面擬合值的誤差組成的向量為ε，各矩陣向量之間的關系［12-13］，如式(2)所示。最小二乘回歸分析使得響應面預測值與有限元模型計算值之間的誤差平方和最小。由式(4)和式(5)可得式(6)四階響應面函數系數向量β。

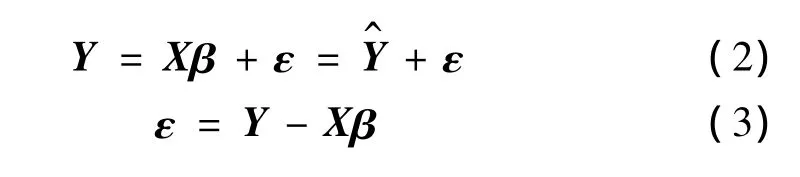
Y為有限元模型計算值向量;Y^為響應面近似函數值向量，ε為擬合誤差向量;待定多項式系數向量β用最小二乘法擬合求解:

其中SSE為誤差平方和。系數向量的估計為:

由此構造出響應面近似函數具體表達式。

2.3 響應面質量檢驗

響應面模型對樣本數據擬合度可用均方根誤差(RMSE)相對值和決定系數R2兩個標準檢驗。RMSE和R2的表達式分別如式(7)和(8)所示。

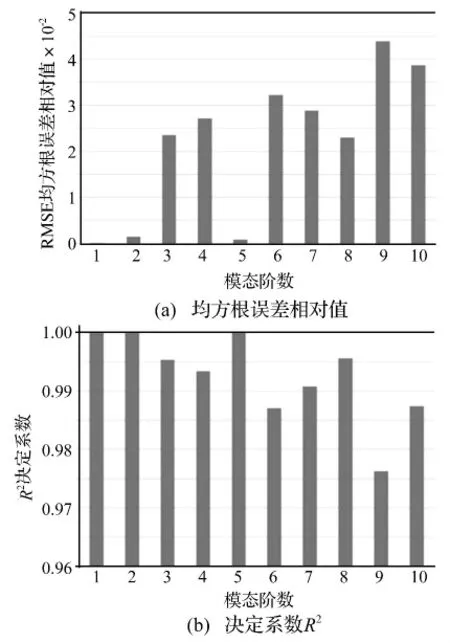
圖5 響應面有效性評價Fig.5 Validity evaluation of response surface

3 基于自適應模擬退火算法的模型參數修正

3.1 目標函數

響應面模型參數修正中的目標函數由實驗實測模態頻率［14］gexpi和響應面模型計算所得模態頻率gi之間的差值構成，其可表示為［15-16］:

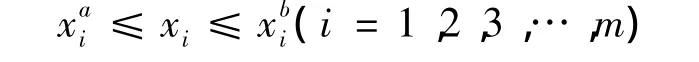
式中:g(x)為響應面計算頻率與實驗實測頻率相對誤差的平方和;為第j階實測模態頻率;gj為第j階響應面計算模態頻率;n為修正頻率的階數;xi為第i個修正參數和分別為修正參數的上下限;m為修正參數的個數。

GARTEUR模型的試驗和響應面計算可得10階模態頻率數據。為驗證響應面法結構模型修正結果的有效性，選取前6階模態頻率作為測試頻段并構造目標函數。后4階模態頻率作為預測頻段，用于修正后的有限元模型預測檢驗。由構建的目標函數可使結構動力學模型修正轉化為采用優化算法尋優的問題。

3.2 自適應模擬退火算法

模擬退火算法源于金屬從高溫向低溫退火從而達到最小自由能態的過程，具有從局部最優點跳出向全局最優點繼續尋優的搜索能力。自適應模擬退火算法(ASA)是在傳統的模擬退火法和模擬淬火過程的基礎上提出的，是一種高效快速的全局優化算法。對先前構建的響應面模型采用自適應模擬退火優化算法(ASA)進行優化分析，求解出GARTEUR模型12個修正變量的最優解，其優化模塊流程，如圖4所示。

將搜索到的最優解代入原有限元模型，所得模型計算模態頻率即為修正模型的頻率值。修正前后有限元模型分析和實測的10階模態頻率的偏差對比，如表2所示。在測試頻段內的前6階模態頻率平均誤差值由修正前的5.73%降低到1.06%;預測頻段內的后4階模態頻率誤差由修正前4.58%降低到1.08%;總平均誤差由5.27%降低到1.07%。可見，修正的有限元模型不但能夠復現測試頻段的頻率而且還能較準確的預測測試頻段外的頻率。初始模型與試驗模型以及修正模型(即優化后模型)的模態頻率對比曲線，如圖6所示。修正的迭代收斂曲線，如圖7所示。

表2 模型修正結果Tab.2 The results of model updating

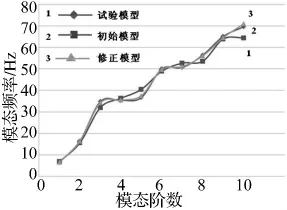
圖6 模態頻率對比曲線Fig.6 Comparation of mode frequency curves

圖7 迭代收斂曲線Fig.7 Iteration convergence curve

4 結論

(1)以優化拉丁方試驗設計抽取樣本點，不完全4階多項式構造響應面，最小二乘法確定多項式系數的方法構建的響應面能夠替代真實模型進行有效、準確的結構動力學模型修正，避免修正過程中多次調用有限元程序，且易于與優化算法結合，提高分析效率和計算精度。

(2)將響應面計算結果與實測結果構造目標函數，利用自適應模擬退火優化算法修正后的模型不僅能在測試頻段內高精度復現結構模態頻率，且能預測測試頻段外的模態頻率，從而驗證了基于響應面法與優化方法相結合的結構動力學有限元模型修正的有效性。

［1］李 輝，丁 樺.結構動力模型修正方法研究進展［J］.力學進展，2005，35(2):170-180.LI Hui，DING Hua.Progress in model updating for structural dynamics［J］.Advances in Mechanics，2005，35(2):170-180.

［2］丁繼鋒，韓增堯，馬興瑞.大型復雜航天器結構有限元模型的驗證策略研究［J］.宇航學報，2010，31(2):547-554.DING Ji-feng，HAN Zeng-yao，MA Xing-ru.Finite element model veri fication strategy of large complex spacecraft［J］.Journal of Astronautics，2010，31(2):547-554.

［3］Heinonen O，Pajunen S.Optimal design of stiffened plate using metamodeling techniques［J］.Journal of Structural Mechanics，2011，44(3):218-230.

［4］Alaswad A，Olabi A G，Benyounis K Y.Integration of finite element analysis and design of experiments to analyse the geometrical factors in bi-layered tube hydroforming［J］.Materials and Design，2011，32(2):838-850.

［5］姜 衡，管貽生，邱志成等.基于響應面法的立式加工中心動靜態多目標優化［J］.機械工程學報，2011，47(11):125-133.JIANG Heng， GUAN Yi-sheng， QIU Zhi-cheng， et al.Dynamic and static multi-objective optimization of a vertical machining center based on response surface method［J］.Journal of Mechanical Engineering，2011，47(11):125-133.

［6］杜家政，隋允康，陽志光，等.基于響應面法的五心底結構形狀優化［J］.計算力學學報，2011，28(6):839-843.DU Jia-zheng，SUI Yun-kang，YANG Zhi-guang，et al.Shape optimization of five center shell structure based on response surface method ［J］. Chinese Journal of Computational Mechanics，2011，28(6):839-843.

［7］Kozak M T，Oztürk M，?zgüven H N .A method in model updating using Miscorrelation Index sensitivity ［J］.Mechanical Systems and Signal Processing，2009，23(6):1747-1758.

［8］D'Ambrogio W，Fregolent A.Dynamic model updating using virtual antiresonances［J］.Shock and Vibration，2004，11:351-363.

［9］Montgomery D C.Design and analysis of experiments［M］.John Wiley ＆Sons，Tnc，2008.

［10］劉曉路，陳英武，荊顯榮，等.優化拉丁方試驗設計方法及其應用［J］.國防科技大學學報，2011，33(5):73-77.LIU Xiao-lu，CHEN Ying-wu，JING Xian-rong，etal.Optimized latin hypercube sampling method and its application［J］.Journal of National University of Defense Technology，2011，33(5):73-77.

［11］Jin R C，Chen W，Sudjianto A.An efficient algorithm for constructing optimal design of computer experiments［J］.Journal of Statistical Planning and Inference，2005，134(1):268-287.

［12］Deniz B，ìsmail H B.Modeling and optimizationI:Usability of response surface methodology［J］.Journal of Food Engineering，2007，78(3):836-845.

［13］Ren W X，Chen H B.Finite element model updating in structural dynamics by using the response Surface method［J］.Engineering Structures，2010，32(8):2455-2465.

［14］Mares C，Mottershead J E，Friswell M I.Results obtained by minimizing natural-frequency errors and using physical reasoning［J］.Mechanical Systems and Signal Processing，2003，17(1):39-46.

［15］丁繼鋒，馬興瑞，韓增堯，等.結構動力學模型修正的三步策略及其實踐［J］.航空學報，2010，31(13):546-552.DING Ji-feng，MA Xing-rui，HAN Zeng-yao，et al.Threestep model updating method in structure dynamics and its application［J］.Acta Aeronautica et Astronautica Sinica，2010，31(13):546-552.

［16］Davoodi M R，Amiri J V，Gholampour S，et al.Determination of nonlinear behavior of a ball joint system by model updating［J］.Journal of Constructional Steel Research，2012，71:52-62.