γ－Reθ轉捩模型的標定與應用

牟 斌，江 雄，肖中云，陳作斌

（中國空氣動力研究與發展中心，四川 綿陽 621000）

0 引 言

轉捩邊界層流動研究在CFD工程應用的許多方面非常重要，如層流翼型、風輪機、輪船船體、渦輪機葉柵等流動特性研究方面。這些流動的雷諾數范圍確定了其層流區域和湍流區域往往具有相同量級，全湍流計算在阻力等方面帶來的偏差不可忽視，必須考慮轉捩的影響。

在過去的幾十年中，全湍流的計算取得了輝煌的成就，并發展起以并行計算、非結構網格為代表的現代CFD技術；而轉捩的數值模擬則嚴重滯后。Menter［1］將其歸結為兩方面的原因：一、轉捩機制復雜，包含了自然轉捩、bypass轉捩、分離誘導轉捩，同時湍流邊界層在順壓梯度下可能再層流化，導致很難用一個簡單的數學模型描述如此多的效應。二、轉捩流動中線性和非線性效應相關，RANS平均消除了線性擾動的增長，因此傳統的雷諾平均方程不能描述轉捩流動。

在工程應用中，考慮轉捩效應的經典方法是經驗關聯，就是把自由流的湍流度和當地的壓力梯度等通過實驗數據關聯到轉捩動量厚度雷諾數，如Abu－Ghannam和Shaw的關聯等。遺憾的是以前的關聯往往是非局部變量的函數，需要作諸如邊界層厚度判定，駐點、分離點查找，沿流線積分等，這些算法受到外形、網格拓撲結構的制約，應用的范圍很窄。

為了與現代 CFD 兼容，Menter與 Langtry［1－5］設計了γ－Reθ轉捩模型。該模型采用經驗關聯的方法，并不模擬轉捩的物理機理。其成功之處在于用應變率雷諾數觸發轉捩，并通過求解額外的兩個輸運方程避免了非局部變量的采用，從而形成與現代CFD相容的框架。在 Menter［2－5］早期的文章中，由于商業保密的原因，兩個重要的經驗關聯函數沒有給出，國外許多學者為了應用，依據平板實驗結果提出了各種in－house公式［6－8］，并在各種 CFD 工程應用中獲得成功；國內空氣動力中心張玉倫［13－14］，西工大張曉東［15］等也提出了各自標定的經驗關系式。雖然2009年Menter及Langtry［1］給出了一組關聯函數，然而，轉捩模型對不同的代碼及標定過程中的微小差異非常敏感，因此這一組關聯函數在CFX中能夠得到很好的結果，在另一個解算器中的表現可能就會差一些［9］。為了較好模擬轉捩效應，有必要在代碼中實現轉捩模型并標定關聯函數。

本文首先在內部軟件mbns3d上實現了轉捩模型，依據零壓力梯度平板轉捩實驗數據確定了一組關聯函數，然后針對A翼型做了驗證計算。隨后數值模擬了NLR7301兩段翼型，研究了轉捩、遠場邊界條件及遠場范圍對精確計算阻力的影響，獲得了有益結論。

1 γ－Reθ 轉捩模型簡介

（1）控制方程

無量綱的γ－Reθ輸運方程的守恒形式為：

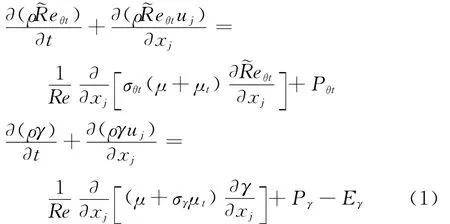
式中各項的詳細解釋可見文獻［5］。

（2）關聯函數

模型中存在三個關聯函數：

對于關聯函數Reθt，不同文獻中的形式略有不同，本文采用Langtry［5］建議的形式。下面的工作是確定其余兩個關聯函數。

2 γ－Reθ 關聯函數的確定

標定工作在內部軟件mbns3d軟件上進行，mbns3d采用多塊結構網格（含拼接、對接、重疊），有限體積求解，具備多重網格、預處理、并行計算功能。

標定計算中，對流項離散選用三階精度的Roe's FDS格式，粘性項二階中心格式離散，AFADI方法求解離散方程。為了適應低速情況和加速收斂，采用了預處理技術和多重網格技術。

標定依據文獻［5］提供的 T3A，T3B，T3A－和Schubauer＆Klebanof等平板試驗數據，試驗條件見表1。

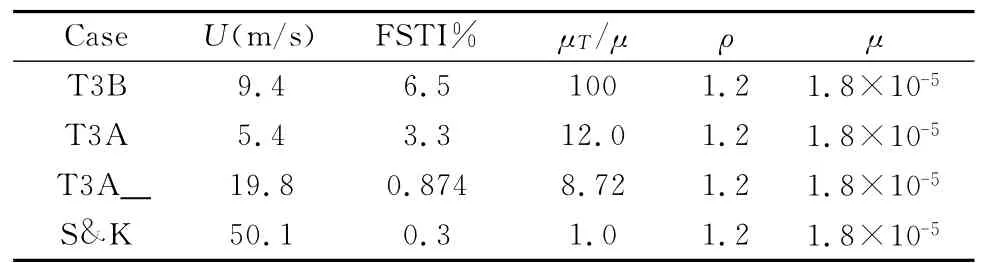
表1 平板轉捩試驗的進口條件Table 1 Inlet condition for the flat plate test cases

平板長度選為2．0，來流遠場邊界距平板前緣0．22，法向遠場邊界距壁面0．22，網格為H型，壁面第一層網格法向距離1．0×10－5，平板前緣第一網格的x向距離1．5×10－3。網格規模為273×97，其中壁面上有241網格點，滿足四重多重網格計算要求。

表1中的FSTI為是平板前緣的湍流強度，由于網格外邊界距平板前緣0．22m，因此外邊界的湍流強度實際上是依據下式估計［5］：

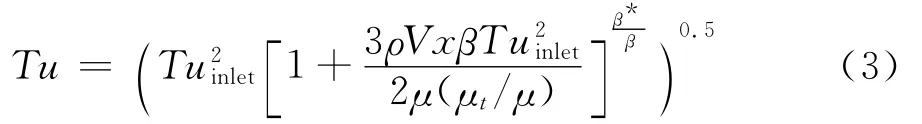
其中β＝0．09，β＊＝0．0828，x是下游距進口的流向距離，V是平均速度。

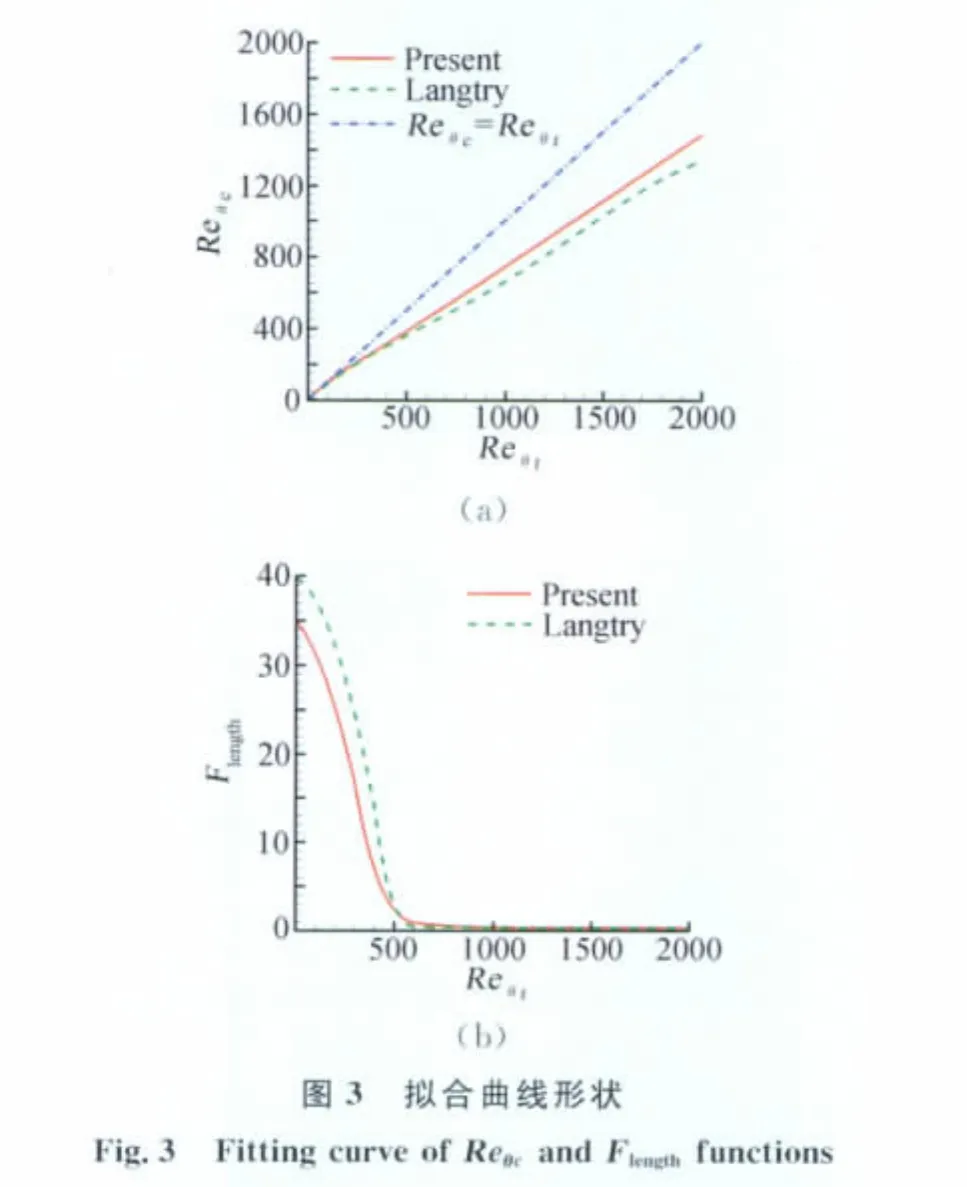
關聯函數中Reθc和Flength是耦合性很強的函數，一個確定，另一個也隨之確定。為了簡便，這里先選定Reθc函數。其選取有一定的原則，保證轉捩能夠發生；在低雷諾數轉捩區盡量大，在高雷諾數轉捩區適當小。這里采用以下形式：

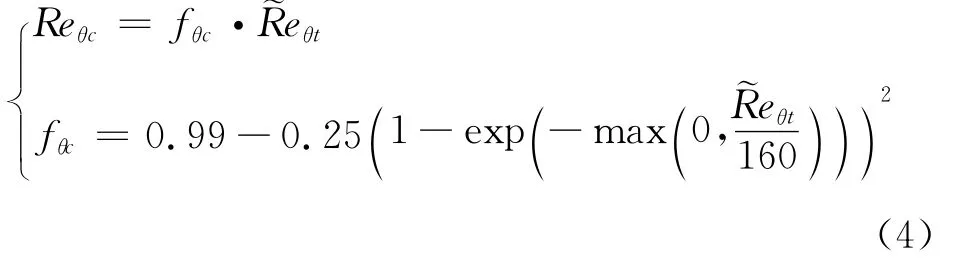
下面的主要任務是確定Flength函數，先選取一個平板算例，按以下幾個步驟進行迭代：

（1）以常數Flength進行計算，并與試驗結果比較，記下與試驗吻合較好的Flength值；

（2）Flength值不變，代入常數Reθc進行計算，當獲得與（1）相同結果時記錄此時Reθc值；

（3）對比Reθc的表達式獲得此時的eθt值；

最后以擬合公式對四個算例進行驗證計算，如有必要，可對Reθc表達式進行適當調整。平板算例中，Flength函數只有在當地值下才對轉捩進行作用，因此，擬合公式幾乎不需要調整。

表2 平板算例關聯函數值Table 2 Correlations for Reθcand Flengthas function ofeθt

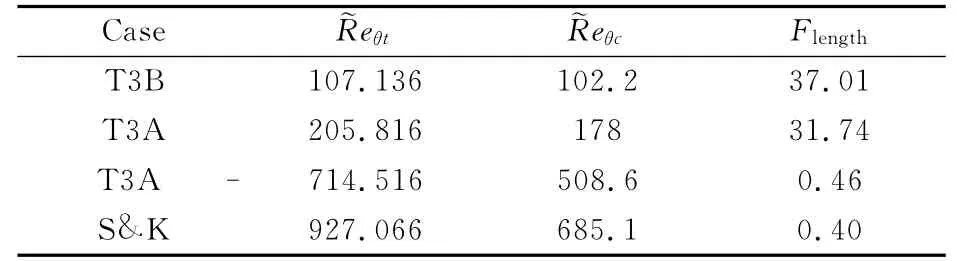
表2 平板算例關聯函數值Table 2 Correlations for Reθcand Flengthas function ofeθt

Case ~Reθt ~Reθc Flength T3B 107．136 102．2 37．01 T3A 205．816 178 31．74 T3A － 714．516 508．6 0．46 S＆K 927．066 685．1 0．40

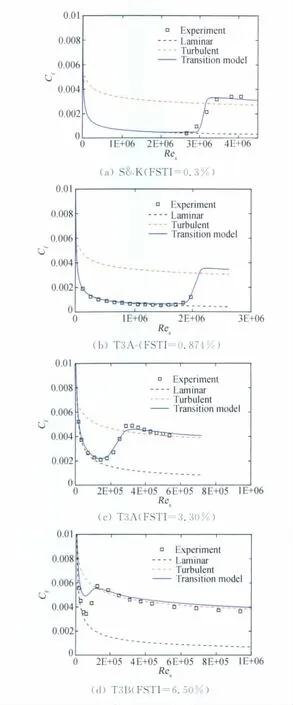
圖1 壁面摩擦阻力系數與試驗的比較Fig．1 Comparisons of skin friction coefficient distribution between CFD calculations and wind tunnel tests

3 驗證算例與討論

3．1 A－aerofoil

A－aerofoil是驗證轉捩模型的標準算例之一。目前存在兩套試驗數據，ONERA F1風洞迎角13．1°和F2風洞迎角13．3°的試驗數據，這里采取了與文獻［5］相同的比較方式。計算參數：M＝0．15，Re＝2．07×106，α＝13．1°，13．3°。湍流度 FSTI＝0．2%，粘性比RT＝10。計算網格（圖4）481×97（流向×法向），遠場延伸100倍弦長，網格第一層1．0×10－5C，滿足y＋≤1的要求。

數值模擬顯示，翼型上表面在0．12C處出現層流分離，且導致分離誘導轉捩，向下游發展為湍流，并在翼型后緣出現湍流分離。轉捩模型計算得到升力為1．5741，阻力 0．0180，試驗值分別 為 1．562、0．0208。全湍流1．4470、0．0282，升力偏小，阻力偏大。與文獻［5］中全湍流阻力差別較大。全湍流結果在后緣與試驗結果吻合更好些。

湍流項和轉捩方程離散均采用二階精度。圖5比較了壓力分布，湍流計算壓力系數比試驗明顯偏低。圖6中比較了湍流及轉捩變量用一階精度離散的摩阻分布，采用轉捩模型大大提高了摩阻計算精度，同時摩阻分布顯示一階精度離散導致轉捩位置略微提前。

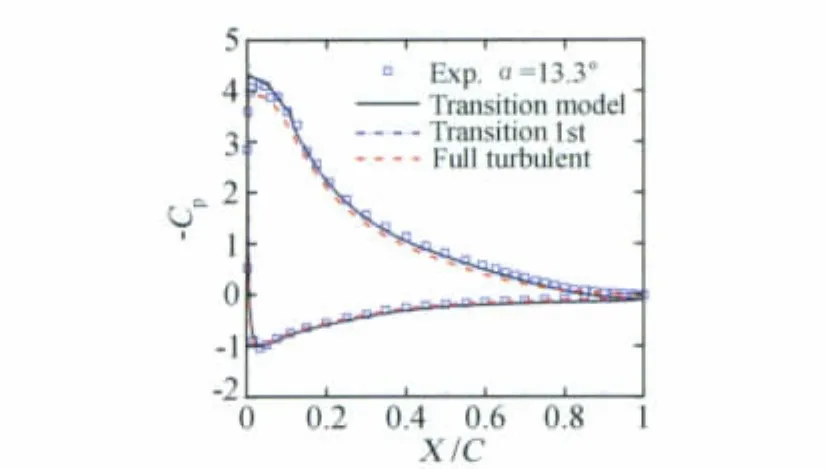
圖5 壁面壓力系數曲線比較Fig．5 Comparison of wall pressure coefficient curve with expriment

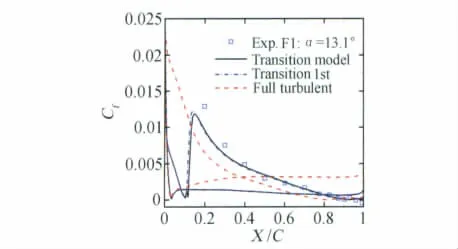
圖6 摩阻系數曲線比較Fig．6 Comparison of wall friction coefficient curve with experiment

3．2 NLR7301兩段翼型

NLR7301兩段翼型的風洞試驗是在70年代末期在NLR3m×2m低速風洞中完成的，試驗結果包括了總體氣動特性、壓力分布、典型站位的速度型分布等多種數據［9］。該翼型的襟翼偏角為20°、來流馬赫數0．185，試驗雷諾數2．51×106、主翼／襟翼重疊區均為5．3%c；試驗構型包含了兩種不同的縫隙寬度，一種為2．6%c，另一種為1．3%c。本文計算了主翼／襟翼的縫隙寬度2．6%c的構型，其中c為弦長。

轉捩模型的應用就是為了提高阻力計算精度，文獻［10］指出，高升力翼型的遠場邊界距離對氣動特性、尤其是阻力特性影響顯著，這要求對遠場邊界進行修正，或者擴大遠場邊界。然而對于本文使用的代碼，遠場邊界取多大合適，這里首先采用環量修正遠場邊界條件在不同大小遠場的網格下進行驗證計算。

環量修正遠場邊界條件其實質為：由于翼型的存在，遠場的自由來流受到了擾動，不再是均勻流動。遠場的擾動可以近似用位于翼型壓心點渦代替，由于阻力一般比升力小2個量級，因此阻力代表的點源不予考慮。點渦誘導速度為：

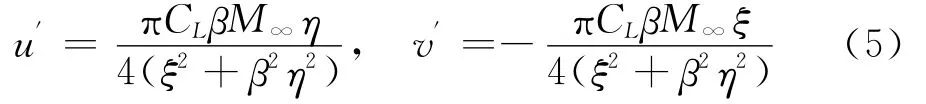
ξ、η為氣流坐標系下坐標。從上式可以看到，誘導速度與升力成正比，與網格遠場范圍成反比，因此在升力較大（如高升力翼型），而遠場不夠遠的范圍下，誘導速度必須考慮。ξ、η表達式為：

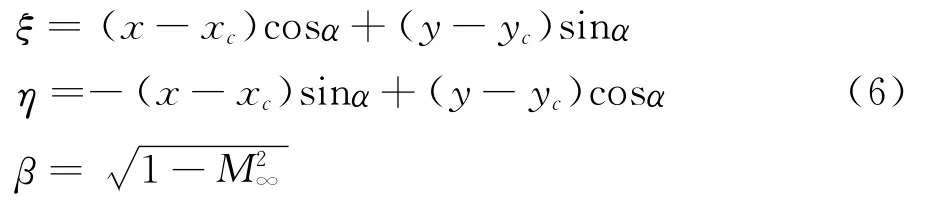
代碼中實際應用的遠場條件通過變化得到：

壓力、密度可以由等熵條件求得。

計算基準網格如圖7所示，為2004年中國空氣動力研究與發展中心與中國航空計算技術研究所聯合舉辦的“CFD統一算例研討”活動發布的標準網格。采用多塊對接結構網格，網格分7塊，網格單元數為15萬，主翼布置457個點，襟翼布置249個點，尾跡區89個，壁面第一層網格距離1．0×10－5c，遠場邊界延伸12c。為研究網格外邊界的影響，這里在基準網格基礎上又做了7套網格進行對比計算。其他網格均是在基準網格基礎上應用雙曲型生成方法推進得到，網格徑向間距放大因子取為1．1，網格生成過程始終保證了大網格內部網格與小網格完全一致，計算迎角為6°。

計算中采用Roe格式，應用4重多重網格及預處理，隱式離散用AFADI求解。翼型湍流度取 ，粘性比RT＝5。在網格外邊界較大時，湍流強度可能衰減厲害，導致計算中轉捩位置偏后，甚至可能出現氣動力振蕩。因此本算例應用了Spalart［11］建議的環境源項法來控制湍流度衰減，本文具體做法是使用物面距離來判斷，即y＞10，控制源項作用，反之則使其自由衰減。也可以使用x坐標來控制。計算中應用了環量修正［12］來作對比計算。

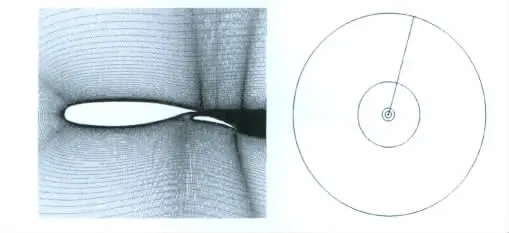
圖7 NLR7301計算基準網格及拓展網格Fig．7 Base grid and big grid of NLR7301

計算結果見表3、表4，對于無環量修正情況，阻力隨著遠場擴大單調減少，升力單調增加，達到6000C后收斂。從120C的結果來看，阻力距離最后收斂值還差了27count。應用標準網格計算的結果與最后收斂值相比大了接近100%。加入遠場環量修正后，網格外邊界達到120C后氣動力就不再變化，且最終收斂值與無環量修正時完全一致。表中CDp為壓力貢獻，CDv為摩擦貢獻。可以看到摩阻貢獻在12C網格下就可以滿足需要，阻力的主要差別在于壓力的阻力分量。

因此，在高升力翼型設計中，計算網格遠場邊界至少應達到100C以上，盡量應用環量修正遠場邊界。

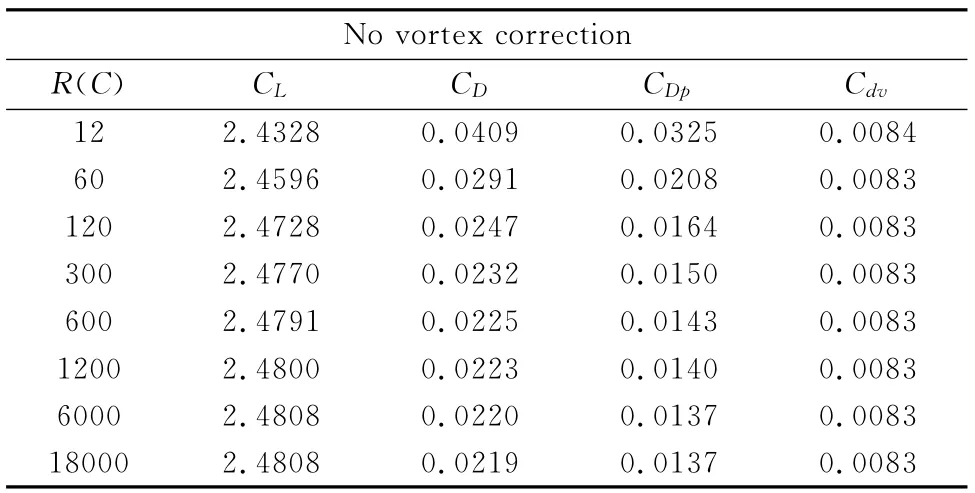
表3 無環量修正時計算的升力、阻力Table 3 Lift and drag without vortex correction

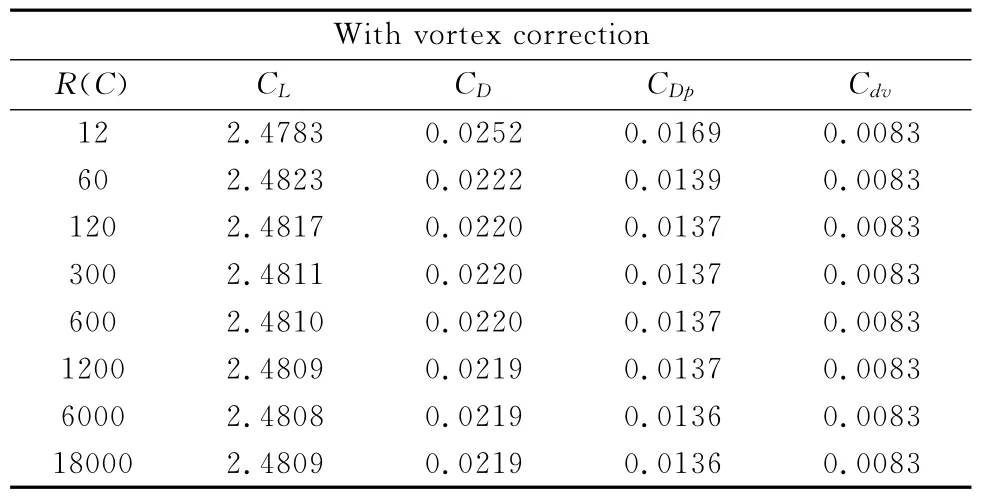
表4 有環量修正時計算的升力、阻力Table 4 Lift and drag with vortex correction

下面以300C的網格計算，加環量修正，研究轉捩對阻力的影響，計算方法及條件同上，分別計算了6°、10．1°、13．1°狀態。計算結果見表5。應用轉捩模型后，阻力最大誤差4%，全湍流計算最大誤差達34．3%。本算例中，轉捩計算提高阻力計算精度的同時，也高估了升力，這是以后應當考慮的問題。

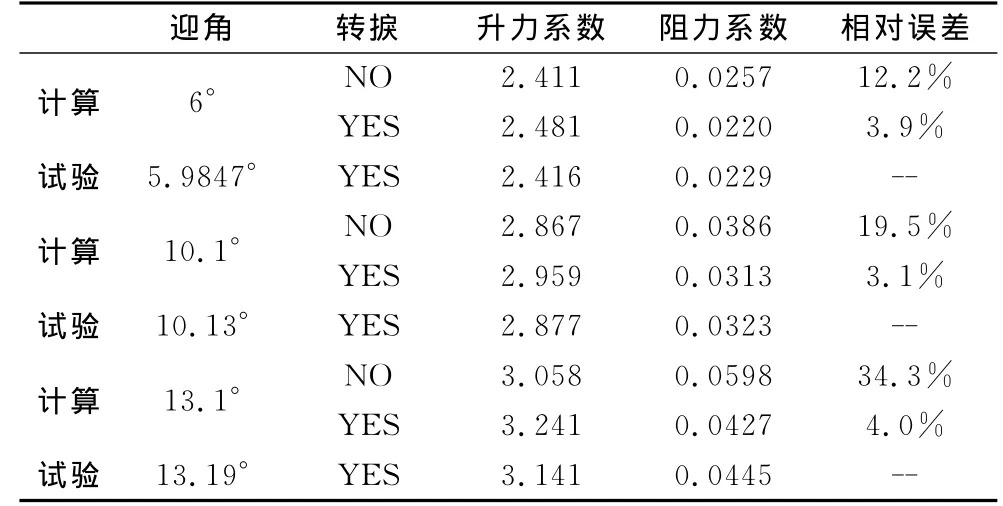
表5 計算升力、阻力與試驗比較Table 5 Comparison of lift and drag with experiment

表6給出了NLR－7301機翼上翼面、下翼面和襟翼上表面的轉捩位置與計算的比較。本文計算中轉捩位置的判定是以摩阻開始增加為依據。從表中可以看到，計算主翼上表面和襟翼上表面轉捩位置與試驗吻合較好，主翼下表面計算轉捩位置靠前。圖8給出了NLR7301不同迎角下的摩阻分布，從圖上可以看到，計算摩阻分布轉捩位置6°和13．1°的結果與試驗轉捩位置很接近，但是在計算中用摩阻系數第一次開始增加來判斷不一定合理。以6°為例，摩阻系數從0．625C位置開始增加，但是增長極其緩慢，在0．68C處存在拐點，從這點開始才急劇增長。同時，圖8結果表明，應用經驗關聯轉捩模型最重要的是關聯函數的標定，由于標定過程均在平板零壓力梯度流動中進行，因此在實際外形流動的表現還有待改進。

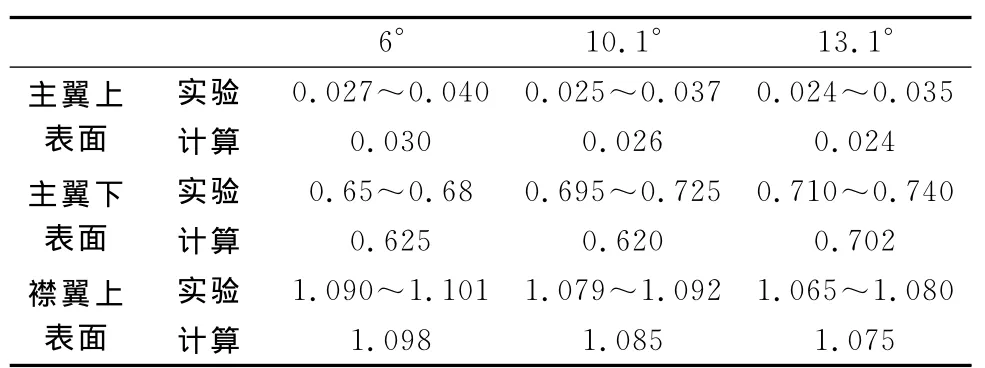
表6 NLR－7301兩段翼型轉捩位置（GA P2．6%）Table 6 Transition location of NLR－7301（GA P2．6%）

圖9的升力、阻力收斂歷程比較可以看到，轉捩與全湍流計算在多重網格迭代2000步后氣動力就不再變化，轉捩對收斂速度影響很小，適合工程應用。圖10給出NLR7301迎角6°湍流強度等值線，圖中白線部分為多塊網格中的間隙。由于轉捩模型采用了輸運方程，因此湍流強度在網格間連續、光滑變化，相應的間歇函數在網格塊間也光滑變化，這在一定程度上增強了代碼的健壯性。

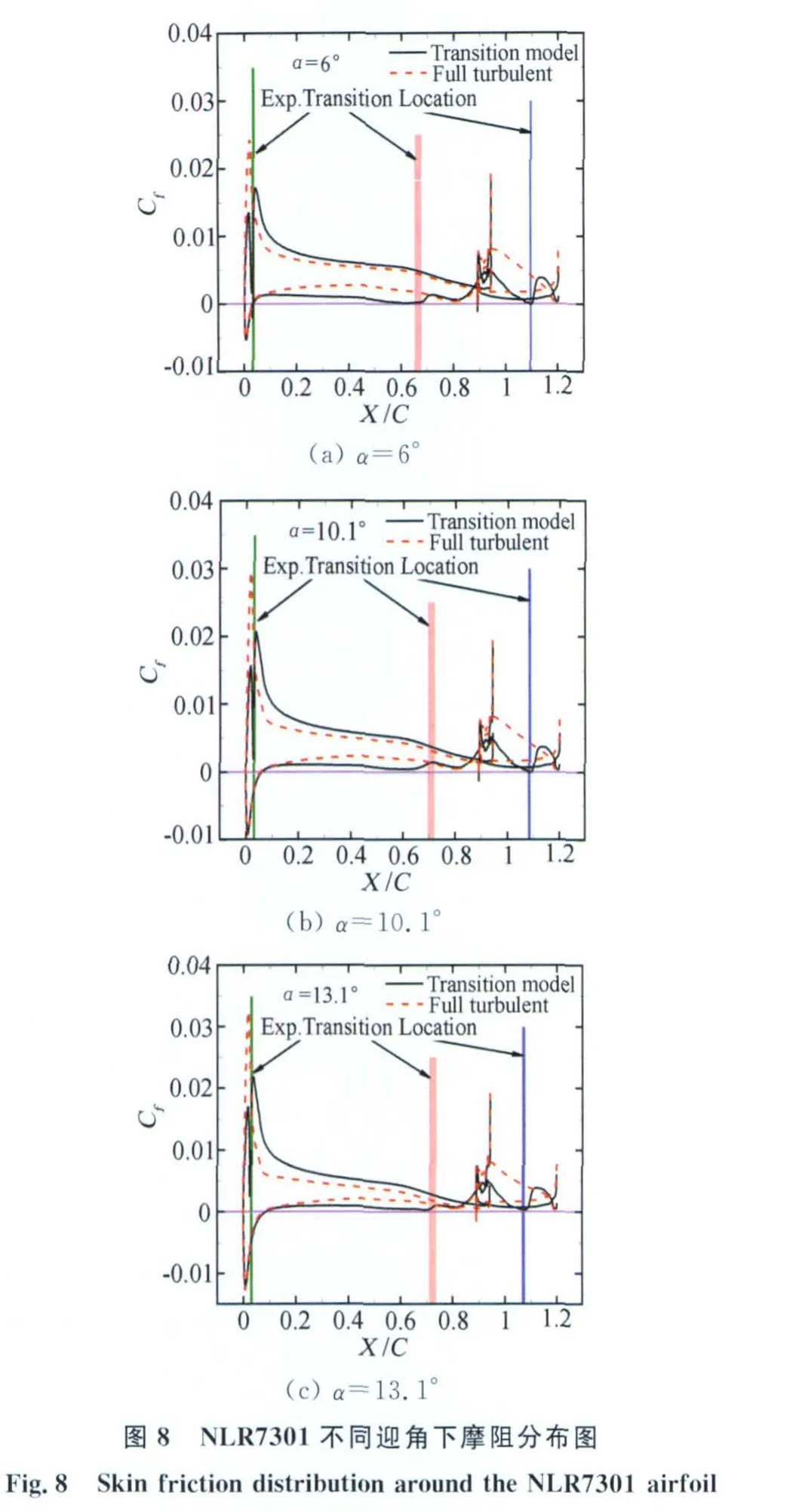
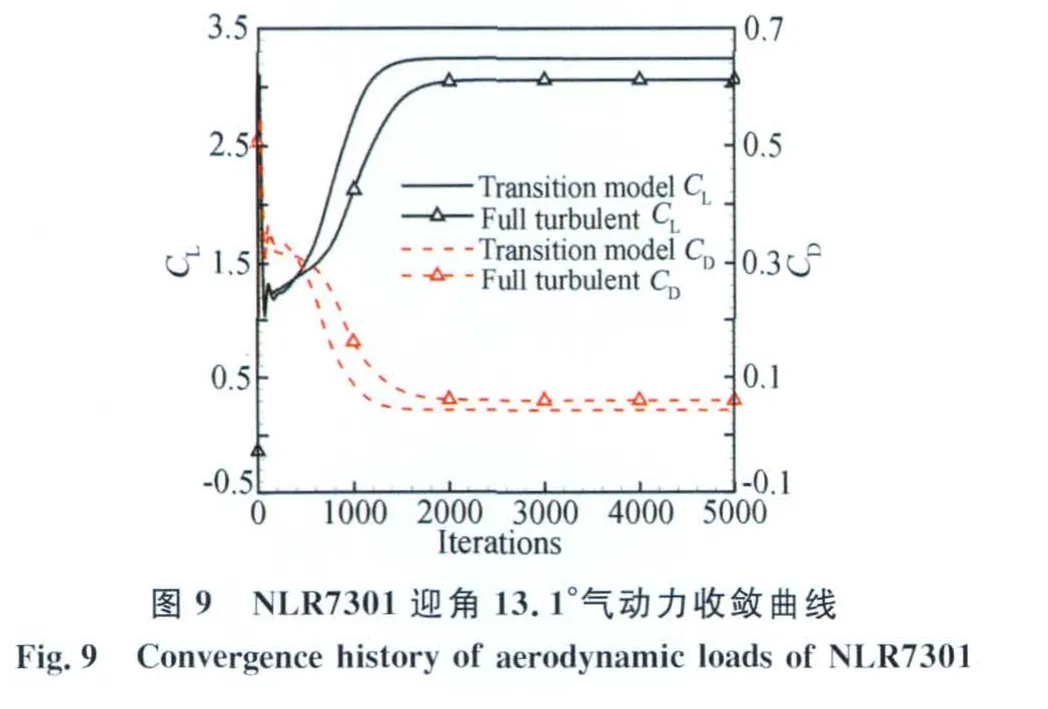
圖10 NLR7301迎角6°湍流強度等值線Fig．10 NLR7301contours of turbulence intensity

4 小 結

（1）應用本文方法確定了一組關聯函數，在平板測試中摩阻系數與試驗吻合較好，說明了本文標定方法的正確性；

（2）A翼型的計算中，轉捩結果的壁面壓力系數及摩阻系數與實驗的吻合程度遠遠好于全湍流計算，說明本文確定的關聯函數在一定程度上能模擬轉捩效應；

（3）NLR7301計算研究表明，要提高高升力翼型阻力計算精度，遠場邊界必須足夠大（100C以上），盡量應用環量修正遠場邊界條件，同時應用轉捩模型。

（4）轉捩模型還很不完善，標定點太少，需要在今后應用中不斷摸索。

致謝：感謝空氣動力學國家重點實驗室張玉倫、王光學、孟德虹同志的熱情幫助。

［1］ LANGTRY R B，MENTER F R．Correlation－based transition modeling for unstructured parallelized computational fluid dynamics codes［J］．AIAA Journal，2009，47（12）：2894－2906．

［2］ MENTER F R，LANGTRY R B，LIKKI S R，et al．A correlation based transition model using local variables：part I－model formulation ASME－GT2004－53452［A］．Proceedings of ASME Turbo Expo 2004［C］，Vienna，Austria，2004．

［3］ LANGTRY R B，MENTER F R，LIKKI S R，et al．A correlation based transition model using local variables：part II－model formulation ASME－GT2004－53454［A］．Proceedings of ASME Turbo Expo 2004［C］，Vienna，Austria，2004．

［4］ LANGTRY R B，MENTER F R．Transition modeling for general CFD Applications in aeronautics［R］．AIAA Paper 2005－0522．

［5］ LANGTRY R B．A correlation－based transition model using local variables for unstructured parallelized CFD codes［D］．［Ph．D．thesis］，Stuttgart，2006．

［6］ MISAKA T，OBAYASHI S．A correlation－based transition models to flows around wings［R］．AIAA Paper 2006－918．

［7］ KARL PETTERSSON，SIMONE CRIPPA．Implementation and verification of a correlation based transition prediction method［R］．AIAA 2008－4401．

［8］ PAUL MALAN，KEERATI SULUKSNA．Calibrating the gamma－Re＿theta transition model for commercial CFD［R］．AIAA 2009－1142．

［9］ VAN DEN BERG B．Boundary layer measurements on a two－dimensional wing with flap［R］．NLR TR 79009U，1979．

［10］CHRISTOPHER L RUMSEY，SUSAN X YING．Prediction of high lift：review of present CFD capability［J］．Progress in Aerospace Sciences，2002，38：145－180．

［11］PHILIPPE R SPALART，CHRISTOPHER L RUMSEY，Effective in flow conditions for turbulence models in aerodynamic calculations［J］．AIAA Journal，2007，45（10）：2544－2553．

［12］THOMAS J L，SALAS M D．Far field boundary conditions for transonic lifting solutions to the Euler equations［R］．AIAA－85－0020．

［13］張玉倫，王光學．γ－Reθ轉捩模型的標定研究［A］．工程湍流轉捩學術研討會［C］．海口，2010．

［14］孟德虹，張玉倫．γ－Reθ轉捩模型在二維低速問題中的應用研究［A］．工程湍流轉捩學術研討會［C］．海口，2010．

［15］張曉東，高正紅．關于補充Langtry的轉捩模型經驗修正式的數值探討［J］．應用數學和力學，2010，31（5）：544－552．