γ－Reθ模式應用于高速邊界層轉捩的研究

孔維萱，閻 超，趙 瑞

（北京航空航天大學 航空科學與工程學院，北京 100191）

0 引 言

在高超聲速飛行條件下，邊界層轉捩直接關系到飛行器摩擦阻力、熱交換及流動的分離位置等，若能準確預測轉捩位置或延遲轉捩的發生，可有效改進飛行器氣動性能，大大降低燃料消耗，使熱防護設計更為靈活。另一方面發動機唇口流動品質是發動機工作的重要參數之一，流動為湍流態時燃氣成分摻混充分，保證燃燒效率；正確控制流動狀態，強制流動發生轉捩已成為高超聲速一體化飛行器設計的重點難題。研究邊界層轉捩及其預測方法，對于飛行器氣動設計和進氣道一體化設計具有重要的工程意義。

風洞實驗一直是研究流動轉捩的重要手段，近年來靜風洞的研究成果［1－3］成為模擬真實飛行狀態流動轉捩和驗證數值方法的重要依據。隨著計算流體力學的發展，數值試驗已逐漸成為與風洞實驗同等重要的流體力學研究方法。其中基于模式理論發展的轉捩模式，以其穩定性和經濟性成為最具有工程應用前景的轉捩模擬和預測方法。Mayle等［4］提出非湍流脈動能概念，模化轉捩前的流動脈動，隨后 Warren等［5］將其耦合在湍流模式中，形成了一方程的轉捩模式。Menter等［6］提出了一種避免求解積分量的基于當地變量的轉捩模式，此模式在眾多亞聲速轉捩流動中表現優秀；值得一提的是該模式特別針對分離導致的轉捩對間歇因子提出了修正，并在部分算例中得到良好的效果。符松和王亮［7］提出了適用于超聲速流動的轉捩模式，該模式統一求解非湍流脈動和湍動能，并以脈動與平均流動的關系作為轉捩起始的判據，考慮多種不穩定擾動模態對了流動的影響。

本文采用γ－Reθ模式對超聲速、高超聲速流動的典型模型進行計算，研究了來流馬赫數、來流雷諾數、攻角狀態和頭部鈍化半徑對流動轉捩的影響，就γ－Reθ模式針對上述流動參數變化的適用性進行討論。

1 計算方法

1．1 控制方程

計算采用有限體積法求解可壓縮全N－S方程，無粘通量由Roe的FDS格式求解，粘性通量采用中心差分格式進行離散，時間推進采用LU－SGS隱式方法。

1．2 轉捩模式

本文采用γ－Reθ模式模擬流動的轉捩。γ－Reθ模式是Menter及合作者［6］提出的轉捩模式，引入渦雷諾數概念將邊界層相關量的求解當地化，建立輸運方程求解間歇因子和臨界動量厚度雷諾數，在SST湍流模式的基礎上實現了對于流動轉捩的計算模擬和預測。

1．2．1 當地雷諾數輸運方程

轉捩起始位置的求解對于轉捩計算和預測至關重要，γ－Reθ模式中求解“臨界動量厚度雷諾數~Reθt”輸運方程從而給出轉捩起始位置的相關信息，與由經驗公式或轉捩判據確定轉捩起始位置的方法相比，此方法能夠更多地反映當地流動特性。當地雷諾數輸運方程表示為：

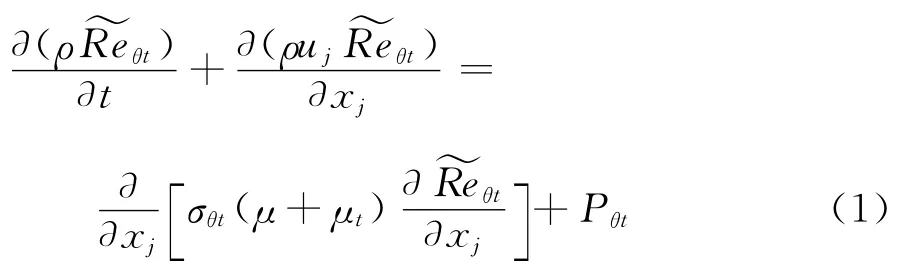
其中生成項為：

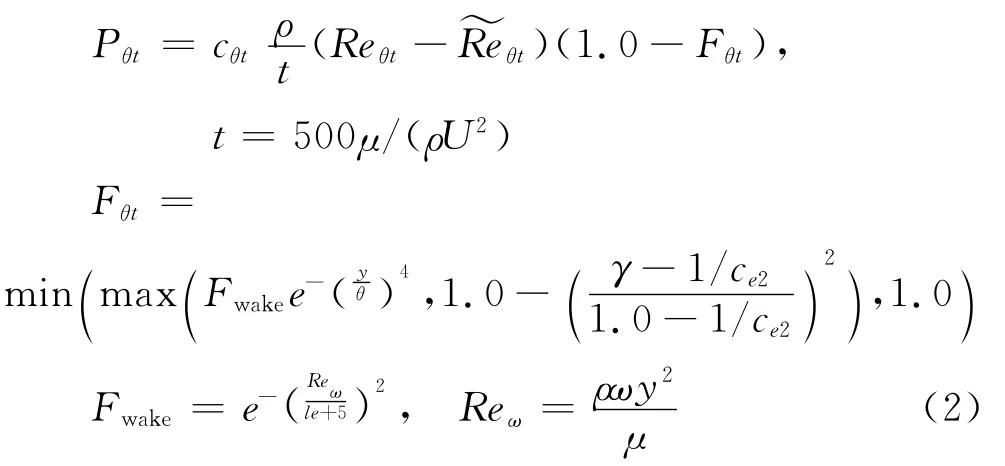
轉捩動量厚度雷諾數Reθt由來流湍流度和壓力梯度等參數擬合的經驗公式，表示為：

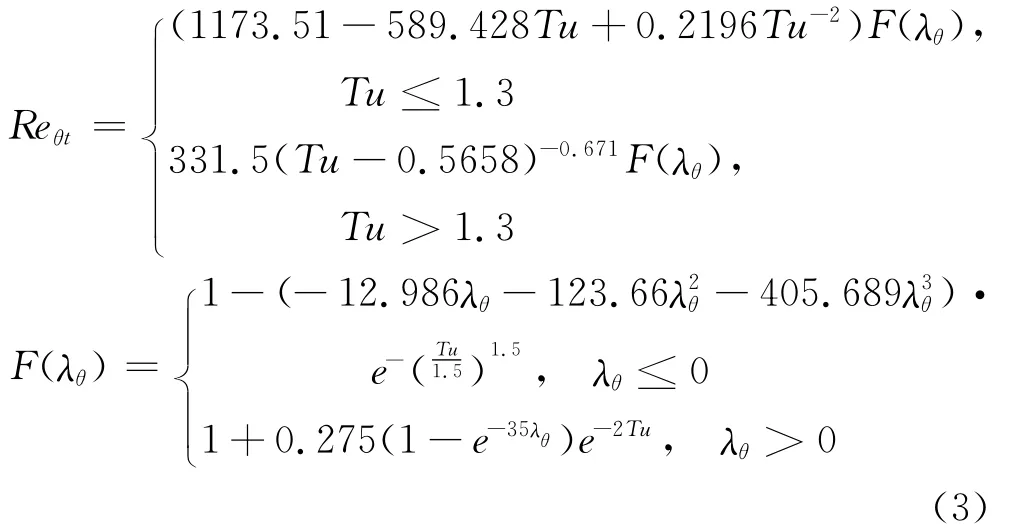
模式常數為：

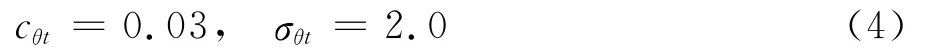
1．2．2 間歇因子輸運方程

將間歇因子作為權值耦合層流與湍流區域的計算，采用輸運方程求解間歇因子，間歇因子輸運方程為：

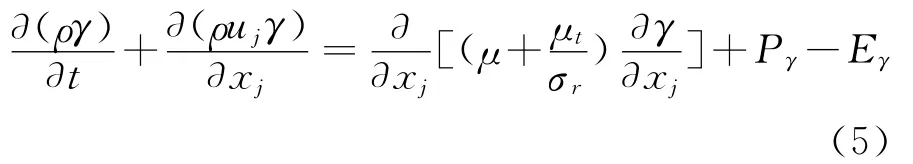
間歇因子的生成項和耗散項分別表示為：

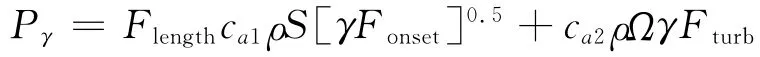
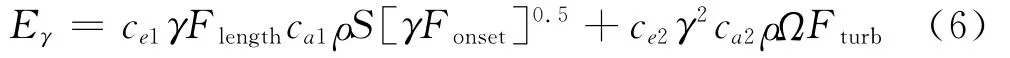
決定間歇因子增長的關鍵參數是Fonset，由下式確定：

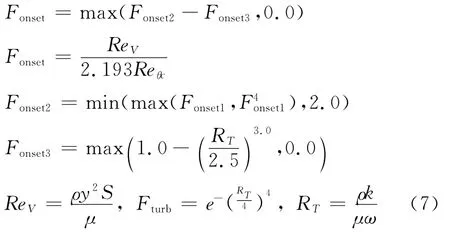
其中Reθc表示間歇因子開始增長處的動量厚度雷諾數，可表示為的函數：

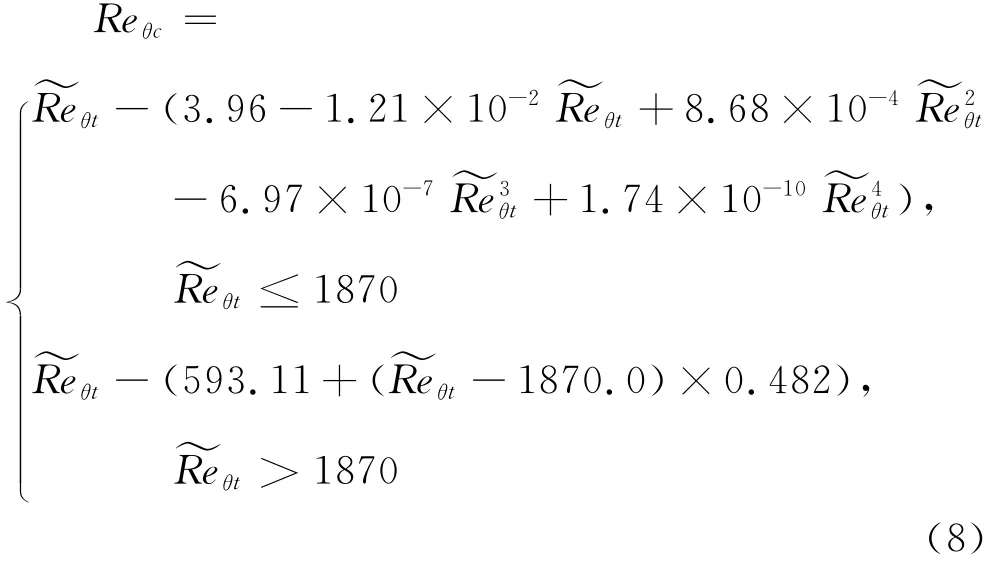
確定間歇因子生成項的另一關鍵參數為Flength，表示轉捩區的長度，同樣以的函數形式給出如下：

其它模式常數為：

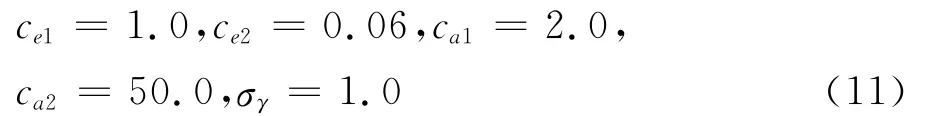
γ壁面法向通量為0；為抑制入口處湍動能的耗散現象，γ設置為1。

1．2．3 模式最終形式

間歇因子體現在原SST模式中湍動能生成項和耗散項中，γ－Reθ轉捩模式的最終形式如下：

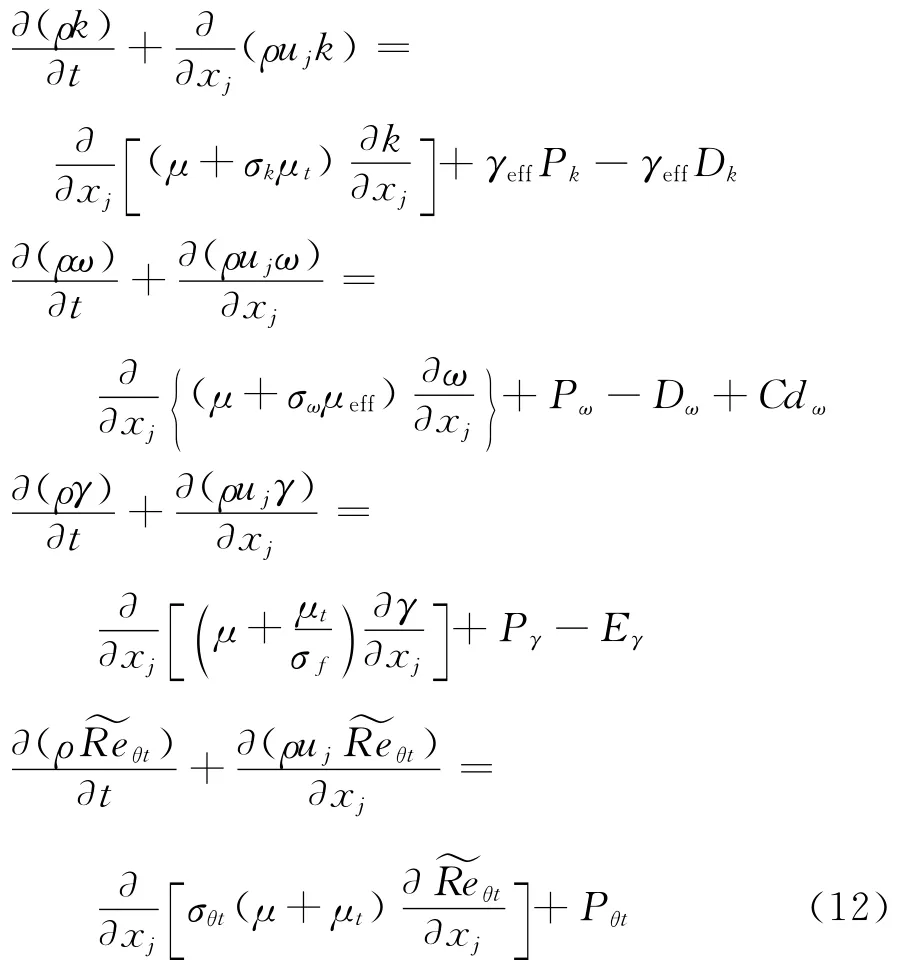
2 數值實驗

2．1 數值格式對轉捩模式的影響

數值格式本身的特性是影響數值模式的關鍵因素之一，這里選取超聲速平板流動算例，采用二階格式包括Roe的FDS格式（分別組合min－mod和superbee限制器）、AUSM＋格式和五階 WENO格式進行計算，研究不同格式對轉捩模擬的影響。超聲速平板流動條件為：來流馬赫數4．5，來流雷諾數6．433×106／m，來流溫度61．1K，來流湍流度0．1%。計算域設置為1m×0．33m，保證法向第一層網格y＋＜1。入口給定速度、壓力、k和ω。

圖1給出壁面摩阻系數沿流向分布情況，比較各種格式計算結果可知：同為二階格式時，限制器的選擇對計算結果的影響明顯，其中壓縮性較強的superbee限制器計算得到的轉捩位置明顯提前于耗散性較大的min－mod限制器結果；不同格式計算結果差異不大；相對于二階格式，高階格式對流動結構的刻畫更為精確，數值耗散小，但計算穩定性差，并對存儲量和計算量提出了更高的要求。對于使用γ－Reθ模式的轉捩預測，計算格式的影響主要體現在格式的耗散性上，耗散較小的計算格式得到的轉捩位置較耗散性大的格式提前，是由于γ－Reθ轉捩模式中控制間歇因子γ生成的函數Fonset與粘性負相關，即體現為數值粘性越小轉捩發生位置越提前。在原有模式參數設置的基礎上，耗散性較大的格式計算結果與DNS數據吻合較好，綜合考慮計算穩定性等因素，下文各算例均采用Roe格式組合min－mod限制器的空間離散方法進行計算。

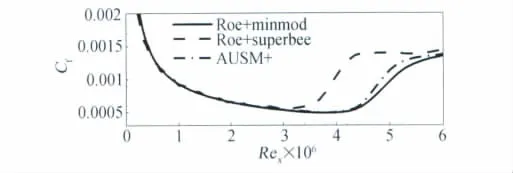
圖1 馬赫4．5平板壁面摩阻系數分布Fig．1 Skin－friction coefficient distribution for M4．5plate

2．2 算例描述

應用γ－Reθ模式計算以下算例：（1）馬赫3．5、半錐角為5°尖錐；（2）馬赫5．91、半錐角5°尖錐；（3）馬赫5．91、半錐角5°裙錐和（4）馬赫7．16、半錐角7°尖錐。其中馬赫3．5尖錐計算了6種雷諾數條件，討論來流雷諾數對流動轉捩的影響。針對馬赫5．91尖錐和裙錐的計算，討論不同攻角狀態對轉捩的影響。7°半錐角尖錐算例中給出了三種頭部鈍化半徑的計算結果，討論頭部鈍化半徑對流動轉捩的影響。

各算例流動參數和計算設置列于表1，需要說明的是，針對各算例分別設置湍動能及比耗散率的入口條件，以盡量保證計算來流湍流度與實驗或參考文獻相同。

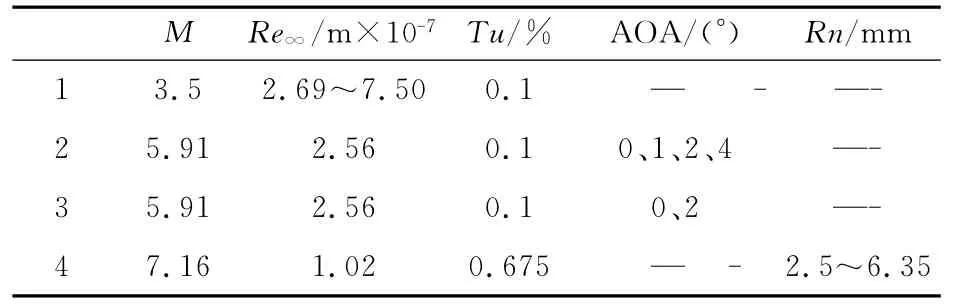
表1 各算例流動參數及網格設置Table 1 Flow condition and grid refinement

以下給出各算例計算結果和討論。

2．3 雷諾數對轉捩的影響

計算長為550mm、半錐角為5°的尖錐，討論不同來流雷諾數條件下流動轉捩情況。流動條件參照實驗［8］設置，來流馬赫數為3．5，來流湍流度為0．1%，來流雷諾數分別為：2．69×107、3．70×107、4．69×107、5．66×107、6．59×107和7．49×107。計算網格設置（流向×法向×周向，下同）為121×121×81，法向第一層網格高度為1．0E－6m；流動入口給定速度、溫度、壓力、k和ω，壁面提無滑移、絕熱條件，出口提遠場條件。

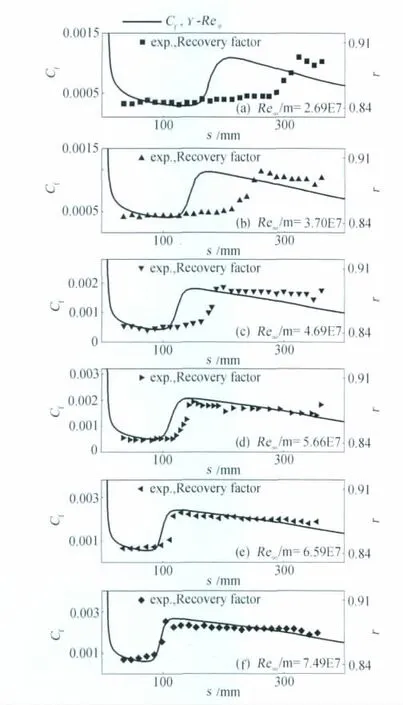
圖2 馬赫3．5尖錐計算結果Fig．2 Skin－friction coefficient distribution for M3．5cone

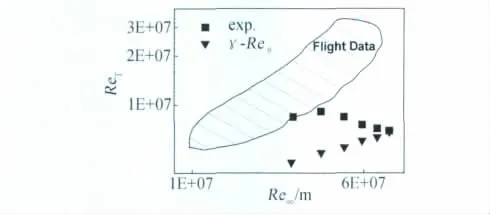
圖3 馬赫3．5尖錐計算結果Fig．3 ReTvs．Re／m from M3．5cone results

圖2 給出馬赫3．5圓錐計算結果，圖中實線（由左側坐標標示）表示壁面摩阻系數，離散點（由右側坐標標示）表示壁面恢復溫度風洞實驗值，恢復溫度定義為r＝（Taw－Te）／（T0－Te）。隨來流雷諾數的增大，γ－Reθ模式計算結果呈現出：轉捩起始位置逐漸向上游移動、轉捩后摩阻系數的峰值逐漸增大的變化趨勢。在較小的來流雷諾數條件下，模式計算的轉捩起始位置明顯比實驗提前，隨著來流雷諾數的增大，這一差異逐漸減小。

圖3比較了飛行實驗、風洞實驗和γ－Reθ模式計算的轉捩雷諾數隨來流雷諾數的變化趨勢。γ－Reθ模式計算結果與飛行實驗變化趨勢相同，可以證實γ－Reθ模式能夠正確反映流動轉捩隨來流雷諾數的變化；但模式計算的轉捩雷諾數整體小于飛行實驗結果，說明γ－Reθ模式未考慮可壓縮性對流動的穩定作用，在超聲速流動（Ma～3．5左右）條件下預測的轉捩位置提前，轉捩雷諾數較小。而風洞實驗結果只在來流雷諾數較小時與飛行實驗結果吻合良好，而隨著來流雷諾數的增大，風洞自身的噪聲很大程度上影響了流動轉捩的結果。

2．4 攻角對轉捩的影響

計算裙錐和圓錐0°～4°攻角流動，討論小攻角對流動轉捩的影響。圓錐長635mm、半錐角為5°；裙錐前半部為長254mm、半錐角為5°尖錐，后半部為曲率半徑2364mm的尾裙，特別設計的曲率半徑使流動在尾裙區域具有逆壓梯度，并保持邊界層厚度不變。頭部鈍化半徑均為0．8mm，裙錐模型幾何外形如圖4所示。

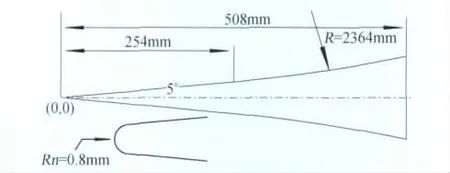
圖4 尖錐裙幾何外形示意圖Fig．4 Geometry for flared－cone

流動參數參照風洞實驗［9－10］設置，來流馬赫數為5．91，來流雷諾數為 9．348E6／m，來流湍流度為0．1%，來流溫度為56．2K。網格設置為121×121×41，法向第一層網格高度1．0E－6m；邊界條件設置與上一算例相同。

圖5為馬赫5．91尖錐裙流動計算結果。圖5（a）給出0°攻角時對稱面壓力等值線分布，除尖錐前緣產生的斜激波外，尾裙區域存在一簇較弱的壓縮波。圖5（b）給出0°攻角母線、2°攻角迎風、背風子午線壓力系數分布。γ－Reθ模式計算的壓力系數與實驗值吻合良好，最大差異在裙錐尾部；圖5（b）中可以看到，實驗結果2°攻角背風面尾裙中部位置出現壓力系數的局部下降，這一流動未能由γ－Reθ模式計算再現。實驗測得0°攻角轉捩發生在x＝371mm位置，2°攻角背風側轉捩位置提前至x＝310mm，迎風側基本保持層流狀態不發生轉捩。計算結果與實驗相同，圖5（c）給出0°和2°攻角壁面法向第一層網格間歇因子分布，0°攻角間歇因子在x＝370mm開始增長；2°攻角時背風子午線間歇因子開始增長位置提前至x＝300mm，迎風子午線間歇因子保持在很小數值。

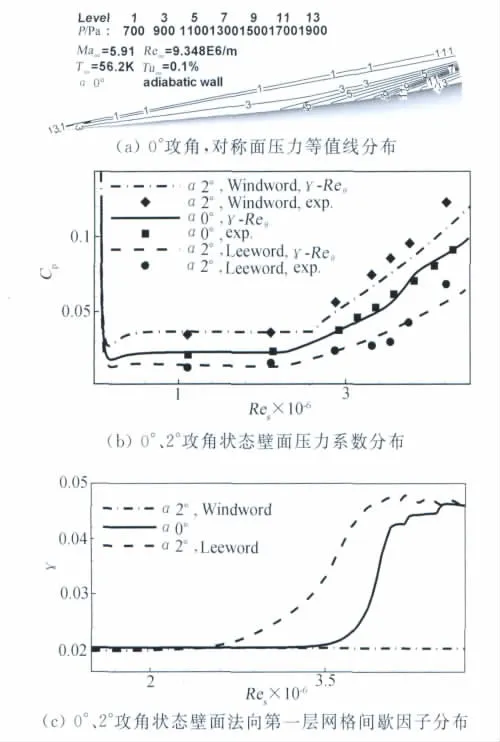
圖5 M5．91裙錐流動計算結果Fig．5 Results for M5．91flared－cone

圖6 給出馬赫5．91直圓錐計算結果。圖6（a）為0°攻角壁面熱流系數與實驗對比，計算結果與實驗值基本吻合，但轉捩起始位置較為提前。圖6（b）給出1°、2°和4°攻角壁面法向第一層網格間歇因子分布。同裙錐計算結果相似，當攻角由0°變為1°時，背風側轉捩位置明顯提前，迎風側轉捩位置推后；隨著攻角的增加，迎、背風側轉捩位置逐漸向下游移動，且周向轉捩線傾斜程度逐漸增大。

分析本節兩算例的計算結果，γ－Reθ模式通過求解當地雷諾數輸運方程得到轉捩起始位置的相關信息，并結合當地雷諾數確定間歇因子，計算能夠一定程度上反應邊界層的三維特性，在未引入橫向不穩定擾動模化的情況下，能夠正確預測小攻角對流動轉捩的影響。

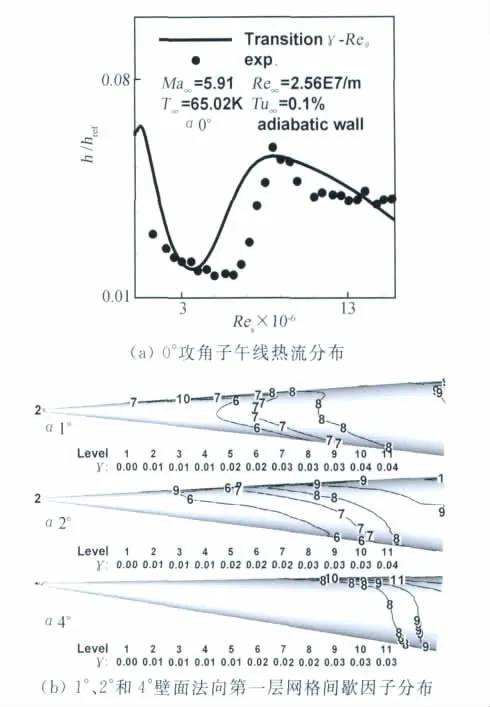
圖6 馬赫5．91直圓錐計算結果Fig．6 Results for M5．91cone

2．5 頭部鈍化對轉捩的影響

最后討論頭部鈍化半徑對流動轉捩的影響，選取長2300mm、半錐角為7°的圓錐進行研究，頭部鈍化半徑（Rn／mm）分別取為2．5、5．0和6．35，以頭部鈍化半徑為特征長度的雷諾數（ReRn×10－4）分別為2．55、5．1和6．477。流動條件參照實驗［11］給定，來流馬赫數為7．16，來流湍流度為0．675%，來流溫度為231．7K，壁面提絕熱條件。計算網格設置為121×121×41，法向第一層網格高度為1．0E－6m；邊界條件設置與上一算例相同。

圖7為馬赫7．16圓錐流動計算結果，圖7（a）和（b）給出頭部鈍化半徑分別為2．5mm和5．0mm時壁面熱流值與實驗對比，熱流峰值的位置和大小等計算結果與實驗值基本相同，但同樣存在預測轉捩起始位置較早的問題。頭部鈍化半徑的變化對于轉捩的影響，主要源于壓力梯度的變化；由于球頭與錐體相接處存在曲率半徑的突變，在該位置產生較大逆壓梯度，從而影響流動轉捩的發生。圖7（c）給出圓錐前緣局部壓力分布及壁面壓力梯度（?p／?s）分布，可見隨著頭部鈍化半徑的增加，逆亞梯度峰值位置逐漸向下游移動；壓力梯度的變化對流動轉捩的影響表現為，隨著頭部鈍化半徑的增加，轉捩位置向下游移動，轉捩后的熱流峰值有一定程度的降低。模式能夠正確模擬頭部半徑對流動轉捩的影響，針對壓力梯度進行了修正提高了對于此類問題的適用性。

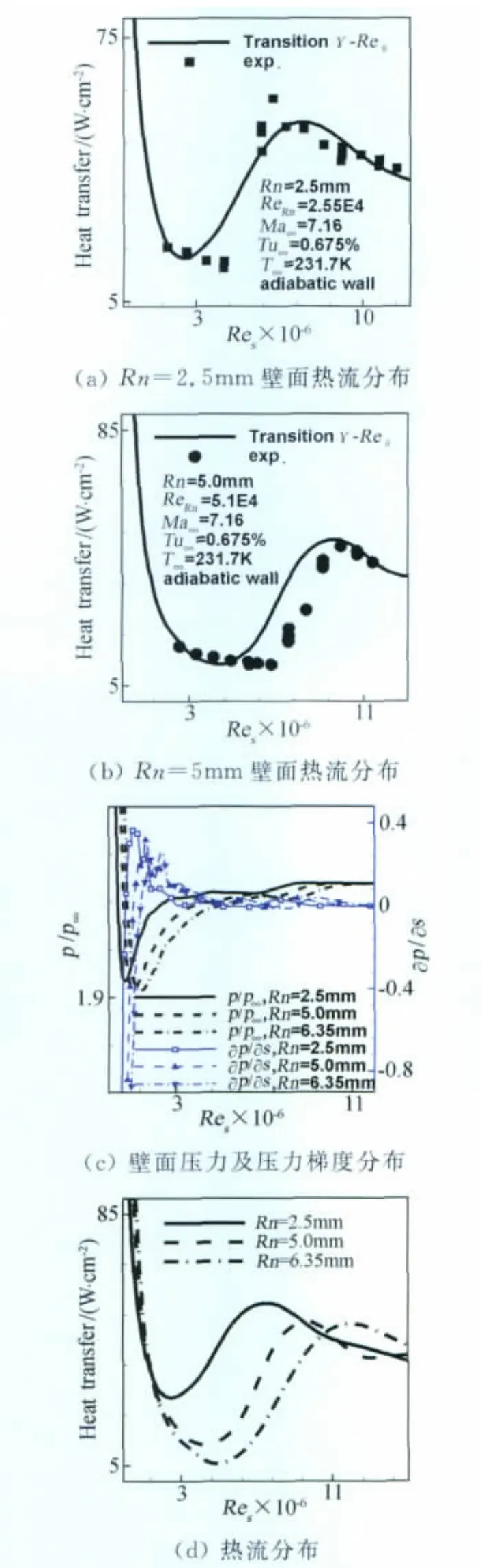
圖7 馬赫7．16尖錐計算結果Fig．7 Results for M7．16cone

3 結 論

（1）將γ－Reθ模式應用于超聲速、高超聲速邊界層轉捩問題的計算，討論了來流雷諾數、攻角狀態和頭部鈍化半徑等關鍵參數變化時的模式性能。數值實驗表明γ－Reθ模式具有一定的預測超聲速、高超聲速轉捩的能力。

（2）馬赫數3至7范圍內的圓錐類流動中，γ－Reθ模式對轉捩位置的預測普遍提前，來流雷諾數較小時尤為明顯。隨頭部鈍化半徑的增大，γ－Reθ模式計算得到的轉捩起始位置后移，對于壓力梯度的變化敏感。

（3）γ－Reθ模式未針對橫流不穩定性進行特別模化，但能夠正確模擬馬赫6圓錐或裙錐小攻角狀態下的邊界層轉捩。相比于0°攻角，小攻角時背風側轉捩位置提前、迎風側轉捩延遲；隨攻角的增加，周向轉捩線變陡峭并向下游移動。

［1］ SCHNEIDER S．A Review of hypersonic boundary layer stability experiments in a quiet Mach 6wind tunnel［R］．AIAA 1997－1819，1997．

［2］ LACHOWICZ J，CHOKANI N，et al．Boundary－layer stability measurements in a hypersonic quiet tunnel［J］．AIAA J．，34（12）：2496－2500，1996．

［3］ CHEN F，MALIK M，et al．Boundary－layer transition on a cone and flat plat at Mach 3．5［J］．AIAA J．，27（6）：687－693，1989．

［4］ MAYLE R，SCHULZ A．The path to predicting bypass transition［J］．J．Turbomach，1997，119：405－411．

［5］ WARREN E，HARRIS J，HASSAN H．Transition model for high－speed flow［J］．AIAA J．，1995，33（8）：1391－1397．

［6］ LANGTRY R，MENTER F．Correlation－based transition modeling for unstructured parallelized computational fluid dy－namics codes［J］．AIAA J．，2009，47（12）：2894－2906．

［7］ 王亮，符松．一種適用于超音速邊界層的湍流轉捩模式［J］．力學學報，2009，41（2）：162－168．

［8］ CHEN F，MALIK M，et al．Boundary－layer transition on a cone and flat plat at Mach 3．5［J］．AIAA J，1989，27（6）：687－693．

［9］ DOGGETT G，CHOKANI N，WILKINSON S．Effects of angle of attack on hypersonic boundary layer stability in a quiet wind tunnel［J］．AIAA J，1997，35（3）：464－470．

［10］HORVATH T，BERRY S，et al．Boundary layer transition on slender cones in conventional and low disturbance Mach 6wind tunnels［R］．AIAA 2002－2742．

［11］JOHNSON H，ALBA C，et al．Boundary layer stability analysis to support the HiFiRE transition experiment［R］．AIAA 2007－0311．