空冷凝汽器U型翅片管水平布置間隙優化

丁麗瑗，陳 帥，程友良

(華北電力大學能源動力與機械工程學院，河北保定071003)

0 引言

直接空冷機組利用空氣直接冷凝汽輪機的排汽，空冷凝汽器翅片管的水平布置間隙直接影響翅片管管外空氣側的冷凝效果，進而影響機組的經濟性[1]。因此，對空冷翅片管水平布置間隙的研究和優化對火電站空冷凝汽器的設計與運行具有重要意義。

近年來，許多學者通過實驗、數值模擬的方法對不同類型翅片管間空氣的流動換熱特性及其影響因素進行了研究及優化。文獻[2]通過CFD對橢圓翅片管進行模擬，計算得到了空冷凝汽器冷卻空氣對流換熱平均努謝爾數Nu和摩擦系數f隨雷諾數Re的變化規律，并得到了相應的關聯式。文獻[3]通過試驗對軋片式橢圓鋁翅鋼管用作換熱器的傳熱及流阻特性進行了測試，并用威爾遜圖解法分離出換熱器兩側的換熱系數。文獻[4]在風洞試驗臺上對8種不同結構參數的百葉窗翅片進行傳熱和流動阻力的性能試驗，同時采用 (j/f)1/3因子綜合評價了8種翅片的強化傳熱效果，并指出翅片長度對強化傳熱的影響最為顯著。文獻[5]用穩態的恒壁溫法對3個橢圓翅片管空冷器和1個圓翅片管空冷器的傳熱和阻力特性進行了試驗研究，得到空冷器空氣側的傳熱與阻力性能，并進行對比。文獻[6]對扁平管外蛇形翅片空間進行數值模擬，并通過PEC指標進行分析、優化。文獻[7]對U型翅片管進行模擬，得出了翅片管換熱量與迎面風速的關系以及最佳翅化比。文獻[8]對波紋管和橢圓翅片管的流動特性和傳熱特性進行數值模擬研究，并對結構參數進行優化。

現有文獻通過實驗和數值模擬，主要分析了不同類型翅片空氣入口風速、翅片間距、翅片高度、斜翅片角度、翅化比對空氣流動傳熱性能的影響，并進行參數優化。對空冷翅片管水平布置間隙的研究和優化，目前還未見到報道。本文以單排空冷凝汽器U型翅片為研究對象，通過簡化的翅片模型，采用數值模擬的方法對不同水平布置間隙下空冷凝汽器U型翅片外側空氣的流動換熱特性進行研究。基于上述研究，針對翅片管的水平布置間隙提出最佳優化方案，并對其進行優化，為空冷凝汽器U型翅片管的設計、布置提供參考依據。

1 物理數學模型及計算方法

1.1 物理數學模型

翅片管的物理模型如圖1所示。其中，翅片管水平布置間隙δ(單位:mm)是研究的變量，分 別 取 0.0，0.4，0.8，1.2，1.6，2.0，2.4，2.8，3.2，3.6共10種情況進行分析。

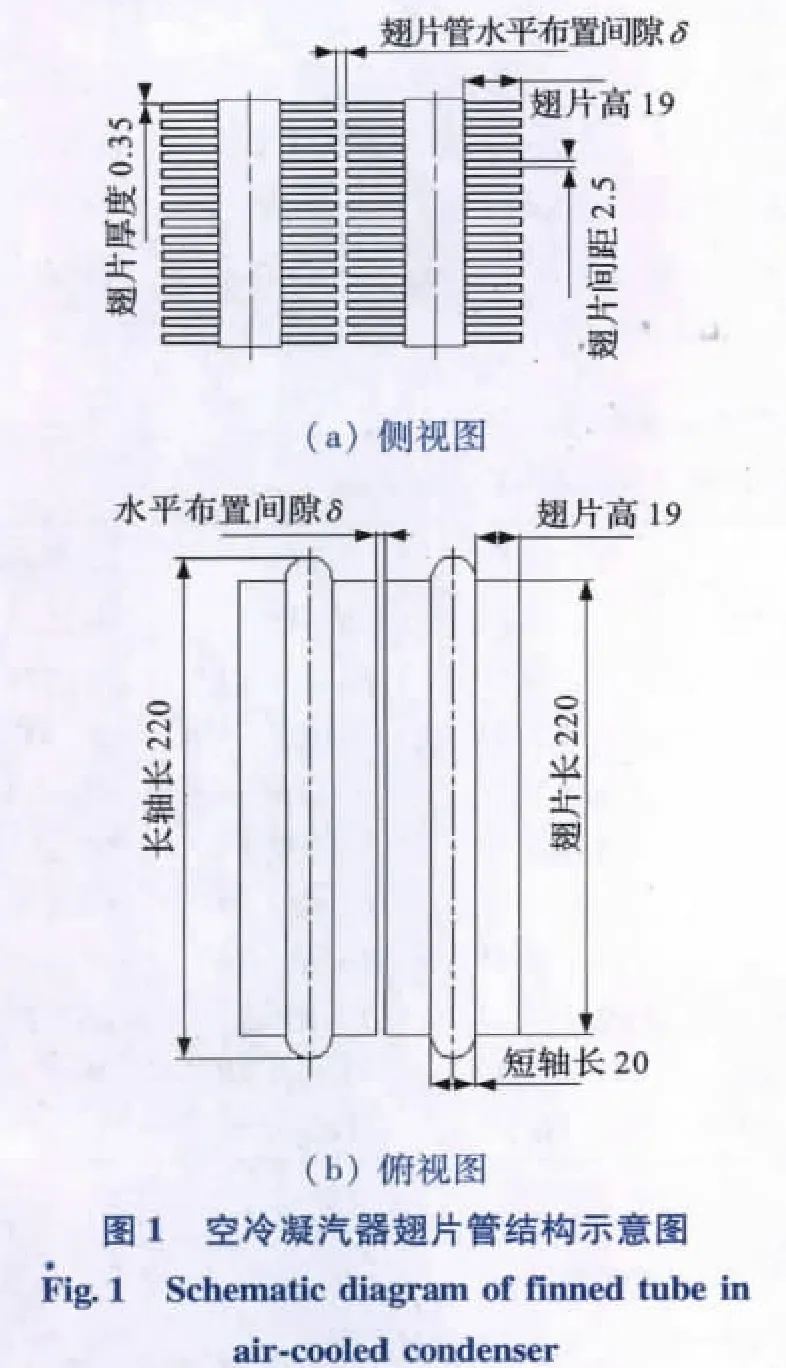
將模型的入口段和出口段延長，使空氣入口流場均勻并且在出口處避免形成回流，整個模型可以分成3段，即入口段、翅片段和出口段，如圖2所示。

圖2 數值模擬計算區域Fig.2 Computational domain of numerical simulation

在以往的模型中，通常采用結構化和非結構化相結合的方法進行網格劃分。為保證網格質量、節省計算資源，本文在此進行了改進[9]:采用了六面體網格，網格總數是384 138個，大部分區域的網格質量不超過0.1，在翅片入口處、出口處基管附近網格質量相對較差，但網格質量最差不超過0.6。

本文采用Fluent軟件進行數值模擬，計算中的控制方程有連續性方程、動量方程、能量方程、湍動能方程和耗散方程。控制微分方程的離散化采用了有限差分法中的控制容積公式法。針對對流項的離散，采用了一級迎風格式。動量方程的離散化采用了交錯網格的方法。壓力與速度的耦合采用Simple算法。

流體假設為穩態流動，且物性參數為定常。由于翅片高度為19 mm，較小，所以翅片壁面、基管壁面均近似取恒壁溫，設為335.98 K;控制體的邊界取對稱邊界;進口為速度入口，出口為自由流動出口。

1.2 計算方法

相關的公式、參數計算如下。

流動阻力

式中:Pin，Pout分別是進口、出口壓力，Pa。

單位時間內流動損失能量

式中:qv為空氣的體積流量，m3/s。

單位時間內空氣側換熱量

式中:qm為空氣的質量流量，kg/s;cp為空氣的定壓熱容，取1 006.43 J/(kg·k)。

平均努謝爾數

式中:h為氣側平均換熱系數，W/(m2·K)，h=Q/A(ΔT)tm;(ΔT)tm為對數平均溫差，(ΔT)tm=[(Tw－Tin)－(Tw－Tout)]/ln[(Tw－Tin)－(Tw－Tout)]，其中，Tw為管壁溫度，為335.98K;TinTout分別為空氣進口、出口的溫度，K[10];λ為空氣的導熱系數為0.023 W/(m·K);de=4A/χ，其中，A為流動面積，m2;χ為潤濕周長，m。

綜合性能評價指標:

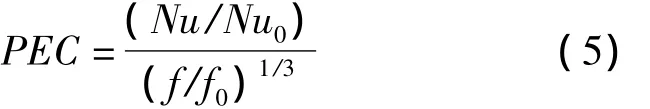
2 結果與分析

在上述10種空冷翅片水平布置間隙下，分別對應7種不同的迎面風速的工況進行模擬，迎面風速分別為1.7 m/s，2.0 m/s，2.3 m/s，2.6 m/s，2.9 m/s，3.2 m/s，3.5 m/s。通過比較分析在不同水平布置間隙下翅片外側空氣在同一風速下的流動換熱特性、相關指標，進行優化。以下是各迎面風速下對應的不同水平布置間隙下的翅片間空氣各流動換熱量及參數的計算結果。

2.1 不同布置間隙下翅片管的特性分析

2.1.1 流動特性分析

通過公式 (1)計算得出翅片間空氣在不同水平布置間隙、不同風速下的流動阻力，并且通過公式 (2)計算得出空氣的流動損失能量，其結果如表1。

如表1所示，流動阻力受水平布置間隙的影響比較明顯。在同一迎面風速下，水平布置間隙從0 mm到0.4 mm，空氣流動阻力有少量的增加;但從0.4 mm到3.6 mm，隨著水平布置間隙的增加，空氣的流動阻力減小。流動阻力在0.4 mm水平布置間隙處達到最大值。如表2所示，水平布置間隙對流動損失能量的影響較明顯，與流動阻力相似。在同一迎面風速下，水平布置間隙從0 mm到0.4 mm處，流動損失能量增大，達到最大值;從0.4 mm到3.6 mm，流動損失能量整體呈減小的趨勢。流動損失能量在0.4 mm處達到最大值。空氣流動損失能量隨水平布置間隙的變化如圖3所示。

表1 空冷翅片間空氣流動阻力計算結果Tab.1 Calculation results of air flow resistance between air cooling fins Pa

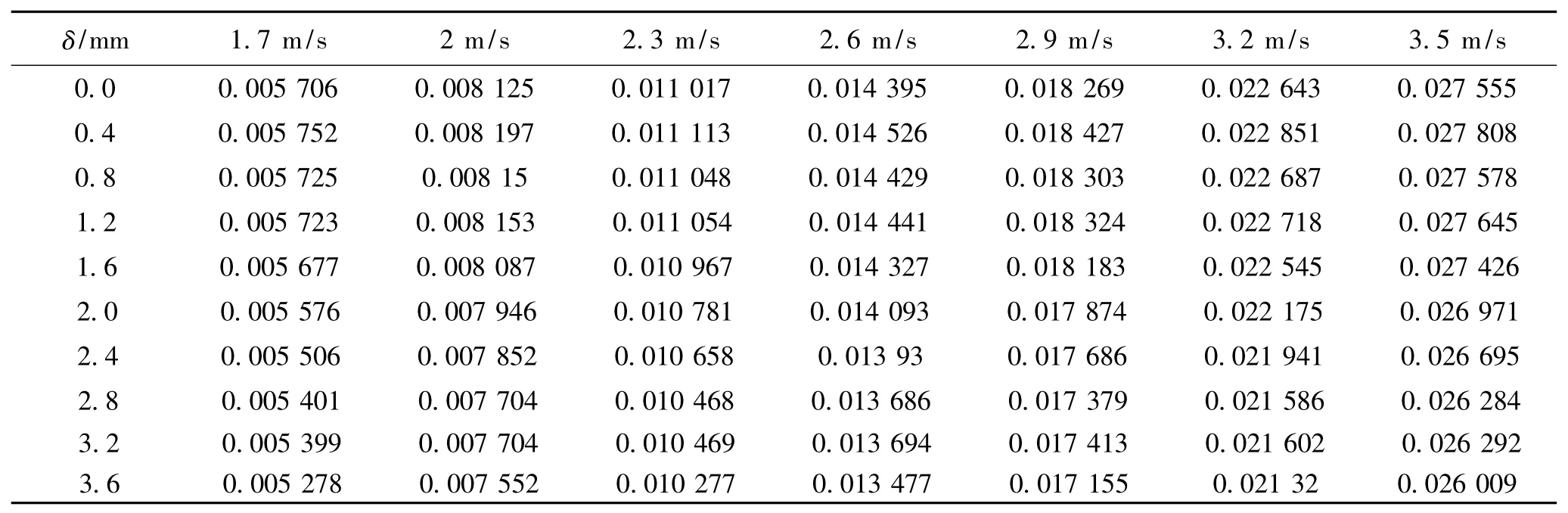
表2 空冷翅片間空氣流動損失能量計算結果Tab.2 Calculation results of air flow loss of energy between air cooling fins W

通過公式 (5)中計算出f，利用最小二乘法對f和Re進行擬合，得出在不同翅片管水平布置間隙下f-Re的關聯式，擬合結果如表3。

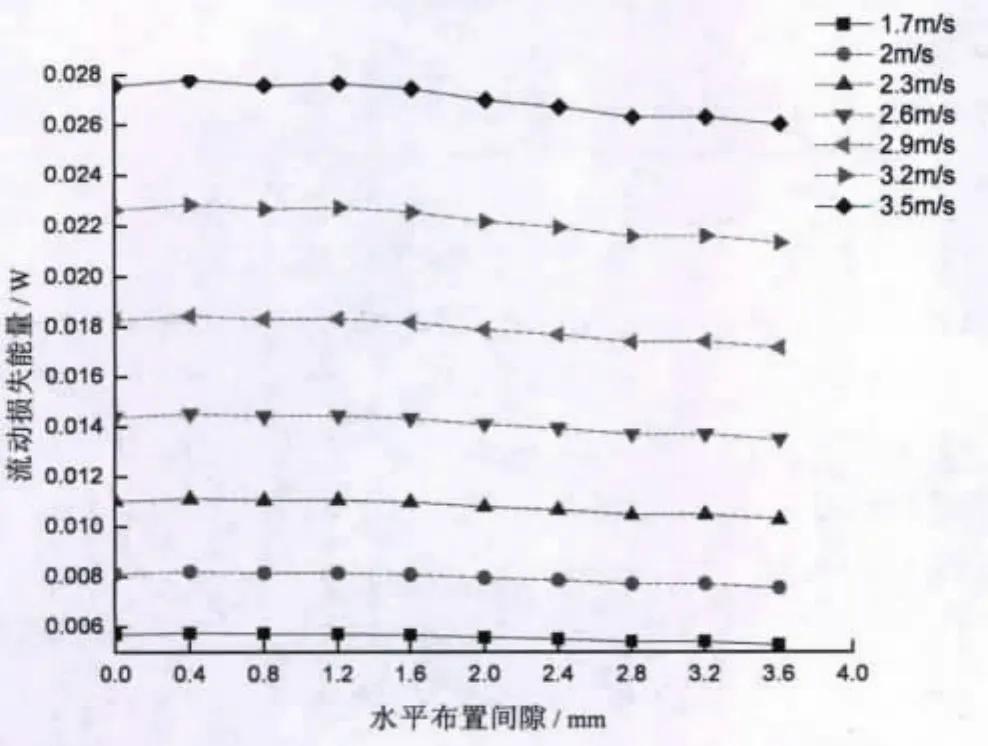
圖3 空冷翅片間空氣流動損失能量隨水平布置間隙的變化Fig.3 Variation of air flow loss of energy between air cooling fins with horizontal arrangement space

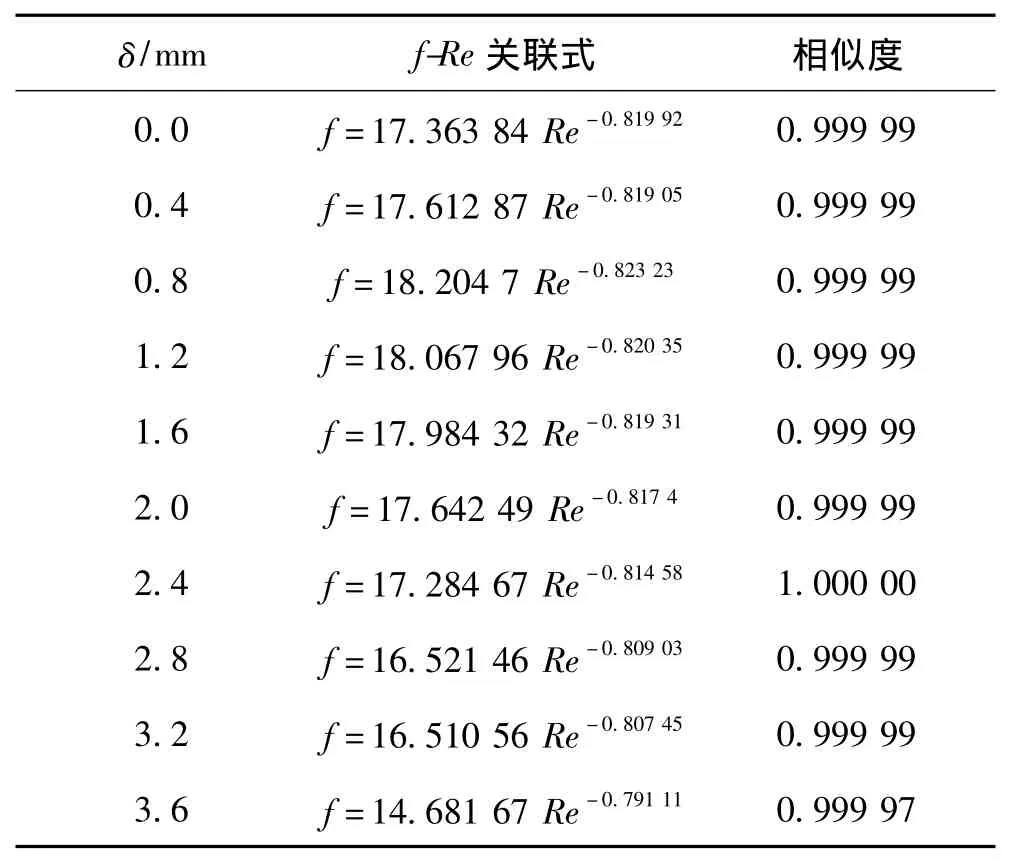
表3 空冷翅片空氣側f-Re關聯式Tab.3 f-Re correlations of air side of air cooling fins

需要說明的是，在計算Re時，本文采用冷卻空氣流經最窄流通截面對應的最大流速。從表3可以看出擬合的相似度基本是0.999 99，擬合質量比較好。

2.1.2 換熱特性分析

通過公式 (3)計算出翅片外側空氣吸收的熱量，空冷翅片的散熱量與空氣的吸熱量相等，再通過公式 (4)計算出Nu數，其計算結果如表4。

從表4可以看出，與流動阻力相似，水平布置間隙對Nu有明顯的影響。在同一迎面風速下，當水平布置間隙從0 mm增到1.6 mm時，隨著水平布置間隙的增加，Nu逐漸增大;從1.6 mm到3.6 mm，隨著水平布置間隙的增大，Nu總體呈減小趨勢。在同一迎面風速下，1.6 mm水平布置間隙處對應的Nu是最大值。

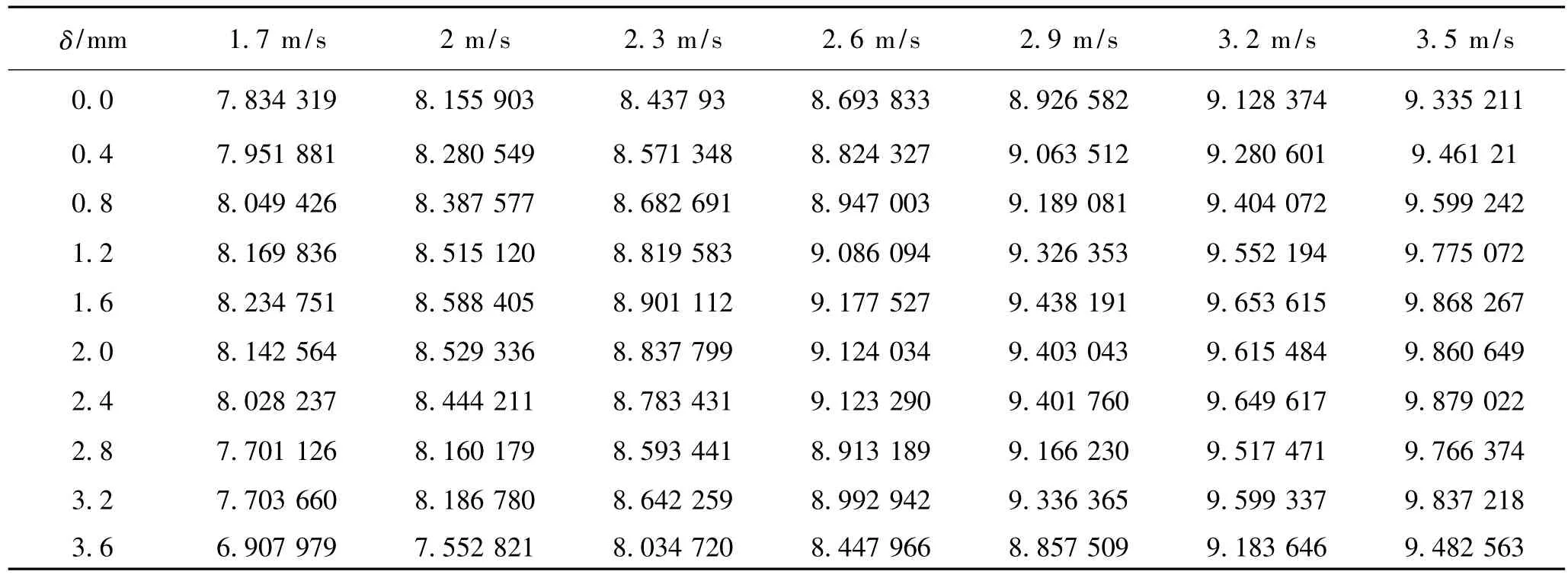
表4 空冷翅片間空氣Nu計算結果Tab.4 Calculation results of Nu between air cooling fins

利用最小二乘法對Nu和Re進行擬合，得出在不同水平布置間隙下Nu-Re的關聯式，其結果如表5。

如表5所示，擬合的相似度基本在0.99以上(3.6 mm處除外)，擬合質量比較好。

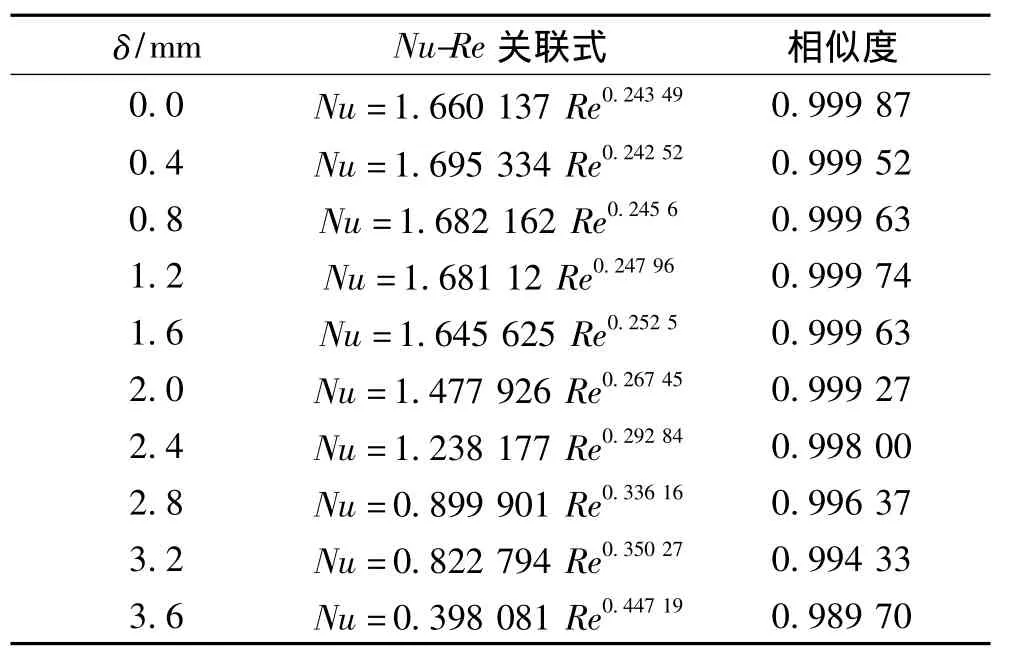
表5 空冷翅片空氣側Nu-Re關聯式Tab.5 Nu-Re correlations of air side of air cooling fins

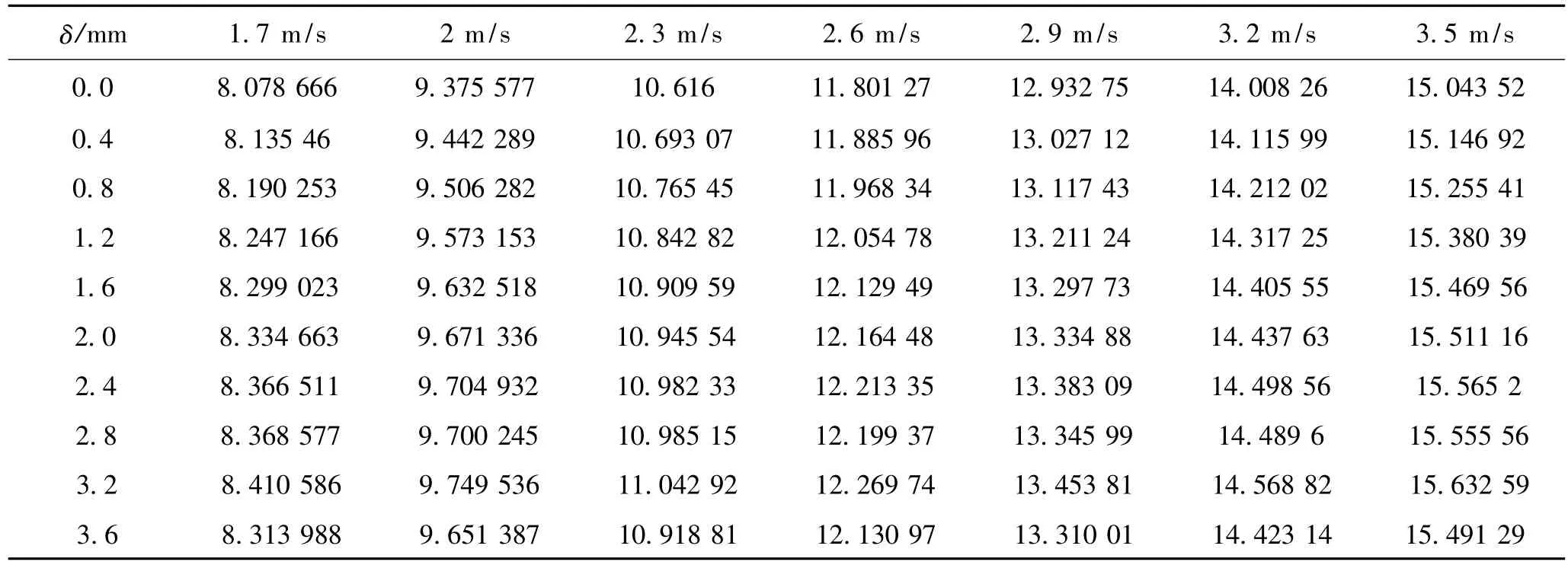
表6 空冷翅片空氣側換熱量計算結果Tab.6 Calculation results of heat exchange between air cooling fins W

如表6所示，水平布置間隙對翅片間空氣換熱量的影響較明顯。其變化規律如下:在同一迎面風速下，換熱量在3.2 mm水平布置間隙處達到最大值。從0 mm到3.2 mm，隨著水平布置間隙的增加，換熱量總體呈增大趨勢;而從3.2 mm到3.6 mm，隨著水平布置間隙的增加，空氣側換熱量總體呈減少趨勢，該變化規律也可以從圖4中直觀地看出來。

對比表2與表6可以看出，與空氣側換熱量相比，流動損失能量很小。以3.2 mm水平布置間隙為例，迎面風速在3.5 m/s時，翅片外側空氣的換熱量為15.632 59 W，其流動損失能量為0.026 292 W，二者相差很大;所以，對于單排空冷凝汽器U型翅片，其流動損失能量可以忽略不計。

圖4 空冷翅片空氣側換熱量隨水平布置間隙的變化Fig.4 Variation of heat exchange between air cooling fins with horizontal arrangement space

由表4和表6對比所示，空氣側換熱量的變化規律與空氣側Nu的變化規律不完全一致。

2.2 翅片管水平布置間隙的優化

關于翅片管水平布置間隙的優化方案，本文采取兩種途徑，一是通過空冷翅片PEC綜合指標進行優化;二是通過選取翅片空氣側換熱量與空氣流動損失能量差的最大值進行優化。兩種方案的優化結果如下。

2.2.1 空冷翅片PEC綜合指標

PEC指標是評價翅片管。綜合性能的指標，其計算如公式 (5)。以1.6 mm水平布置間隙處的Nu0，f0為基準進行計算，其計算結果如表7。

表7 空冷翅片PEC指標計算結果Tab.7 Calculation results of PEC indicator of air cooling fins

PEC指標達到最大值時，表明相應風速下，水平布置間隙達到最佳。由表7可見，在不同的迎面風速下，其最佳水平布置間隙是不同的。迎面風速在1.7 m/s到2.9 m/s范圍內，最佳水平布置間隙是1.6 mm;在3.2 m/s到3.5 m/s范圍內，最佳水平布置間隙是2.4 mm。顯然在水平布置間隙從0 mm到最佳布置間隙、從最佳布置間隙到3.6 mm兩個區間內，從總體來看，是先增大后減小的趨勢，在最佳水平布置間隙處取得最大值。

當迎面風速為2.9 m/s時，2.4 mm處的值與1.6 mm處的值相差－0.000 82;當迎面風速為3.2 m/s時，二者的值相差0.002 454;在迎面風速為3.5 m/s時，二者的值相差0.003 924。因為二者之差逐漸增大，所以，從這個趨勢上可以看出，風速在2.9 m/s到3.2 m/s這個范圍內，對應的最佳水平布置間隙從1.6 mm過渡到2.4 mm。

空冷翅片PEC指標隨水平布置間隙的變化如圖5所示。

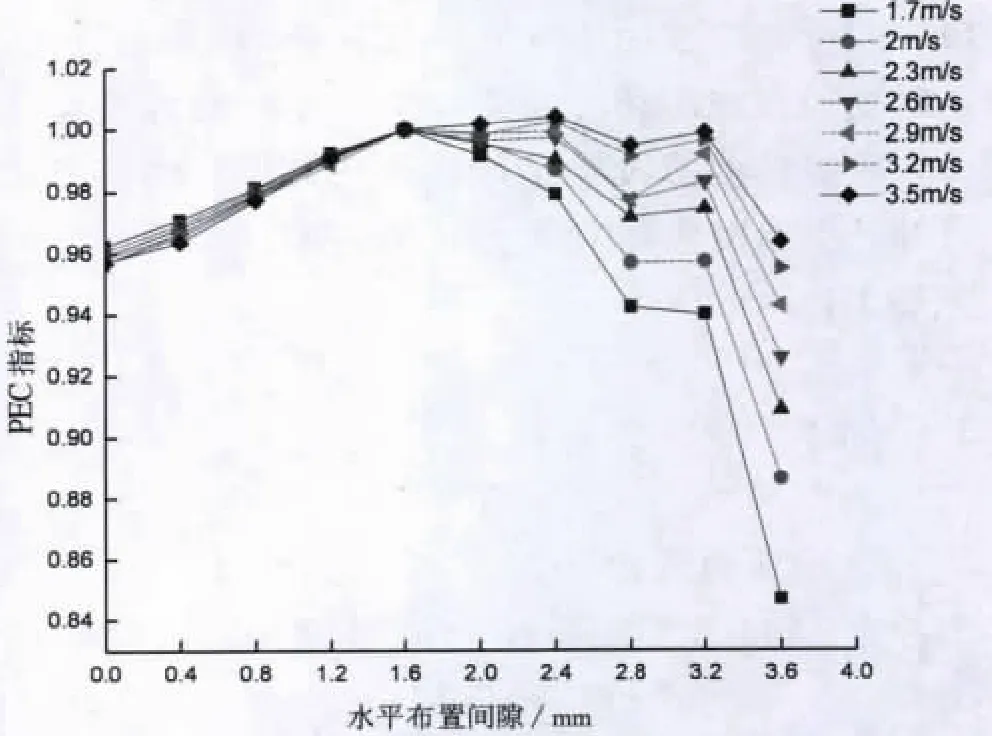
圖5 空冷翅片PEC指標隨水平布置間隙的變化Fig.5 Variation of PEC indicator of air cooling fins with horizontal arrangement space

2.2.2 能量差值方案

通過上述計算出的翅片外側空氣換熱量與空氣流動損失能量的差，與其最大值對應的翅片管水平布置間隙就是最佳水平布置間隙。

但是從表2和表6的對比可以看出，與換熱量相比，流動損失能量較小，可以忽略不計。所以，最佳水平布置間隙主要是由翅片空氣側換熱量決定。由表6可以看出，在3.2 mm處，翅片間空氣換熱量最大，所以，翅片管的最佳水平布置間隙是3.2 mm。

能量差值方案考慮的是翅片的空氣側換熱量與流動損失能量的差，它更加直觀地反應出翅片的換熱效果。

2.2.3 兩種優化方案的比較

由表7可知，空冷翅片PEC指標方案的優化結果與能量差值方案的優化結果不同。造成這種結果的原因主要有:(1)PEC綜合指標考慮流動阻力的影響較多;但是因為在不同迎面風速下，與翅片間的空氣換熱量相比，單排U型翅片管的流動損失能量較小，可以忽略不計;(2)在不同的水平布置間隙下，空氣側換熱量與空氣側的Nu的變化規律不完全一致，所以，空冷翅片PEC指標與能量差值方案的優化結果不同。

因此，當流動損失能量較小時，空冷翅片PEC指標不能準確反應出空冷翅片管的綜合性能，此時要通過空冷翅片換熱量來對空冷翅片進行優化，故能量差值方案是最佳優化方案。由該方案可知，空冷凝汽器U型翅片管的最佳水平布置間隙是3.2 mm。

3 結論

(1)與換熱量相比，單排空冷凝汽器U型翅片管中的空氣流動損失能量較小，可以忽略不計。

(2)通過兩種方案的比較，結果表明:當流動損失能量較小時，空冷翅片PEC指標不能準確反應出空冷翅片管的綜合性能，此時要通過空冷翅片換熱量來對空冷翅片進行優化;空冷凝汽器U型翅片管的最佳水平布置間隙是3.2 mm。

(3)本文通過最小二乘法對不同水平布置間隙下空氣側的f-Re，Nu-Re進行擬合，得出了相關的關聯式，可為空冷凝汽器U型翅片管的設計、布置提供一定的參考依據。