反射式橢圓高斯光束平頂整形系統

孟祥翔，劉偉奇，柳 華，魏忠倫，康玉思，馮 睿，呂偉振

(1.中國科學院長春光學精密機械與物理研究所，吉林長春 130033; 2.中國科學院大學，北京 100049)

1 引 言

激光自問世以來得到了廣泛的應用。在光刻[1]、激光醫療[2]、材料加工[3-6]、全息[7]等技術領域，往往需要光強分布為平頂函數的圓形或方形激光光束。現在對激光光束平頂化整形主要有采用二元光學元件[8]、液晶空間光調制器[9]、雙折射透鏡[10]、基于幾何光學方法設計的折射(或反射式)透鏡[11-15]等方法。采用幾何光學方法設計的激光光束平頂系統因其具有高能量利用率和適用于高功率激光等優勢得到了廣泛的應用。目前，采用幾何光學方法設計的折射式激光光束整形器[11-13]已發展成熟。為整形效果不受入射光波長影響且適用于高功率激光，Malyak[14]首先提出了無中心遮攔的反射式高斯光束整形系統。部分準分子激光光束[15]和使用單片非球面準直的半導體激光光束均可近似為橢圓高斯光束，在準分子激光醫療等領域往往需要光斑形狀為圓形的激光光束，所以必須對橢圓高斯光束進行平頂化整形。Vladimir Oliker[16]在對兩鏡光束整形系統的研究中提出了一組二階非線性偏微分方程描述反射鏡面形，其優點是不受入射光束和出射光束對稱性的影響，在入射面和出射面坐標關系確定的情況下，可以將任意分布的準直入射光束整形為所需分布的準直出射光束，但是對于二階非線性偏微分方程組的數值求解和編程比較困難。

本文介紹了將橢圓高斯光束轉化為圓形平頂光束的無中心遮攔反射式兩鏡整形系統的設計方法，給出了兩反射鏡積分形式的面形方程，簡化了設計步驟，并針對美國GAM LASER公司的EX5/250 ArF準分子激光器設計了整形系統，分析了系統參數對整形效果的影響。

2 理論分析

采用幾何光學方法設計激光光束平頂整形器的主要依據是能量守恒、折/反射定律、等光程條件[12]。利用能量守恒推導出入射面坐標和出射面坐標的對應關系;然后利用標量或矢量形式的折/反射定律進行光線追跡，代入等光程條件，即可求出整形系統的面形方程[15]。

2.1 坐標關系

圖1(a)為反射式橢圓高斯光束整形器在y-z平面的原理示意圖，假設入射光束和出射光束都平行于光軸，輸入光束和輸出光束在x-y平面上的剖面圖如圖1(b)所示，定義(r，θ)為入射面的極坐標，(ρ，φ)為出射面的極坐標。

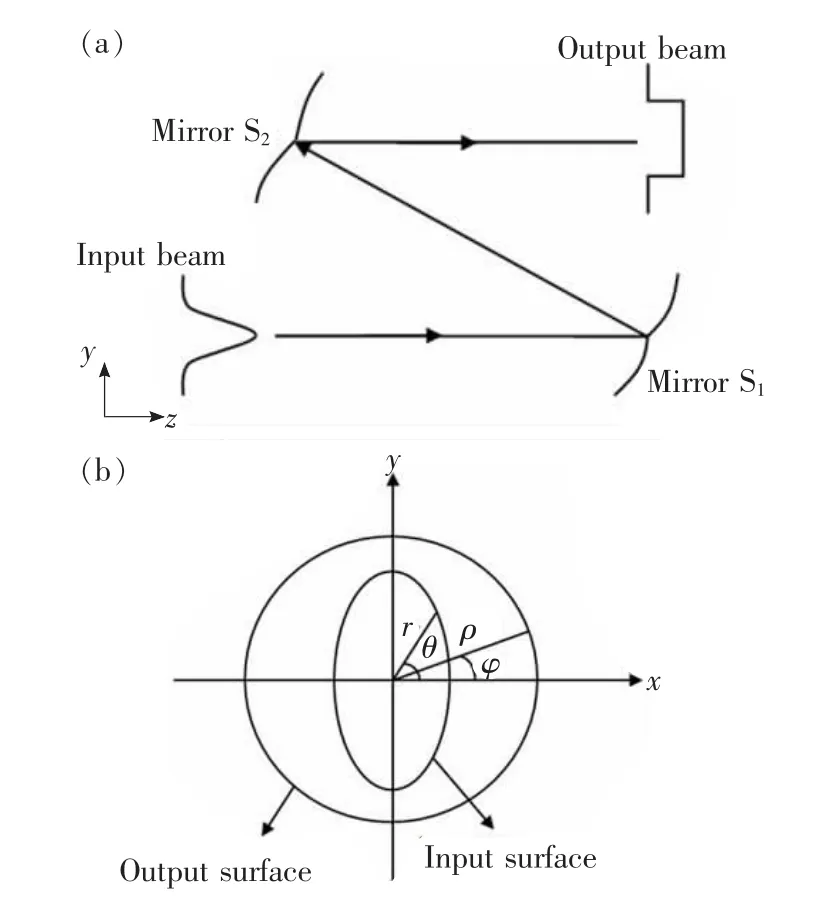
圖1 反射式激光光束整形系統示意圖。Fig.1 Scheme reflective laser beam shaping system.

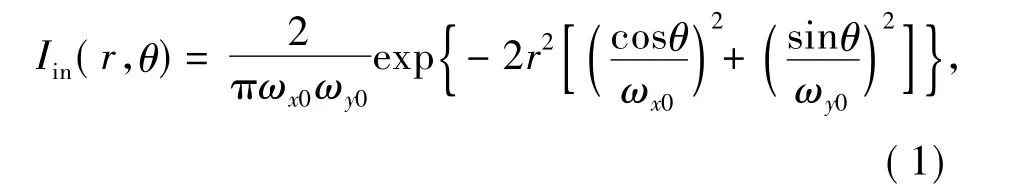
設入射橢圓高斯光束光強分布方程為其中ωx0和ωy0分別為橢圓高斯光束x和y方向上的束腰，定義 ωy0/ωx0=m。

為方便積分，采用勻化洛倫茲函數作為出射光強分布:

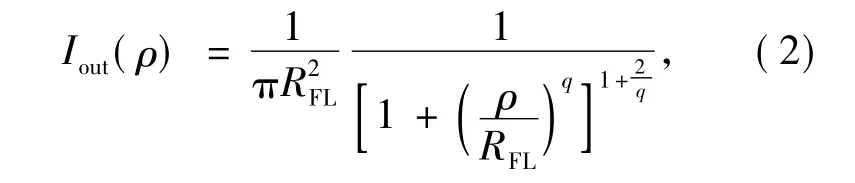
式中RFL為出射平頂光強分布的半高寬。q決定著勻化洛倫茲函數的形狀，選擇合適的q值，即可得到目標出射平頂分布。

針對橢圓高斯光束這種非旋轉對稱形式的光束輪廓，根據能量守恒定律要求有

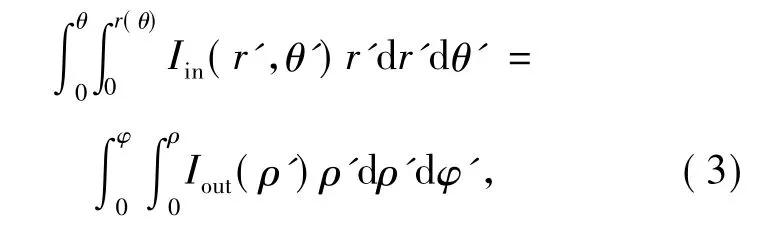
橢圓方程的極坐標形式為

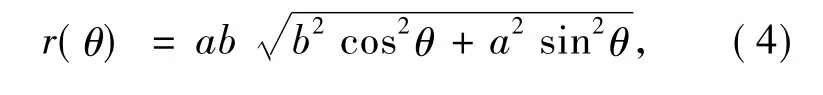
其中a、b分別為橢圓的短軸半徑和長軸半徑。為便于之后的運算選擇積分路徑，設a=r0，b/a=n，則b=nr0。當n取定值時，橢圓方程可化為

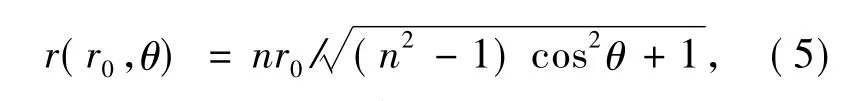
令n=m，則入射橢圓光束光強分布可化簡為

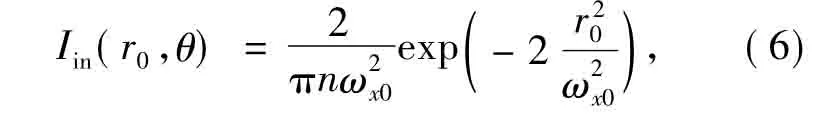
將式(2)、(5)、(6)代入式(3)，可得:

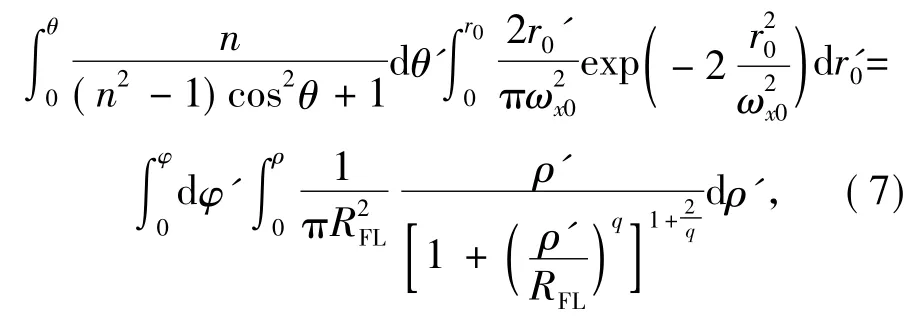
分離變量可求得(r0，θ)與(ρ，φ)的坐標關系為

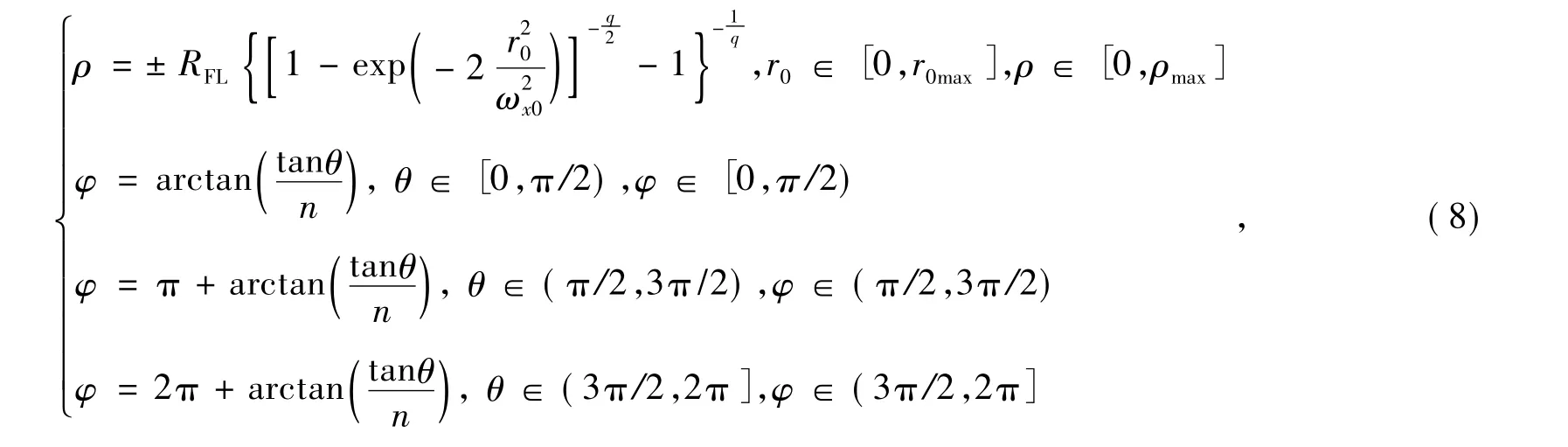
當θ=π/2時，φ=π/2;當 θ=3π/2時，φ=3π/2。其中ρ與r0的關系中取正號代表系統無實焦點，取負號代表系統有實焦點。當n值一定時，r0的大小就確定了一個橢圓，(r0，θ)則能唯一確定橢圓圓周上的一個點且r0與θ無關。此時即可將入射面看作無數個幾何中心相同，長軸與短軸之比一定的橢圓的集合，每個橢圓在經過系統變換后與出射面上的一個圓對應，這樣就實現了光束形狀由橢圓到圓的變換。

2.2 面形方程

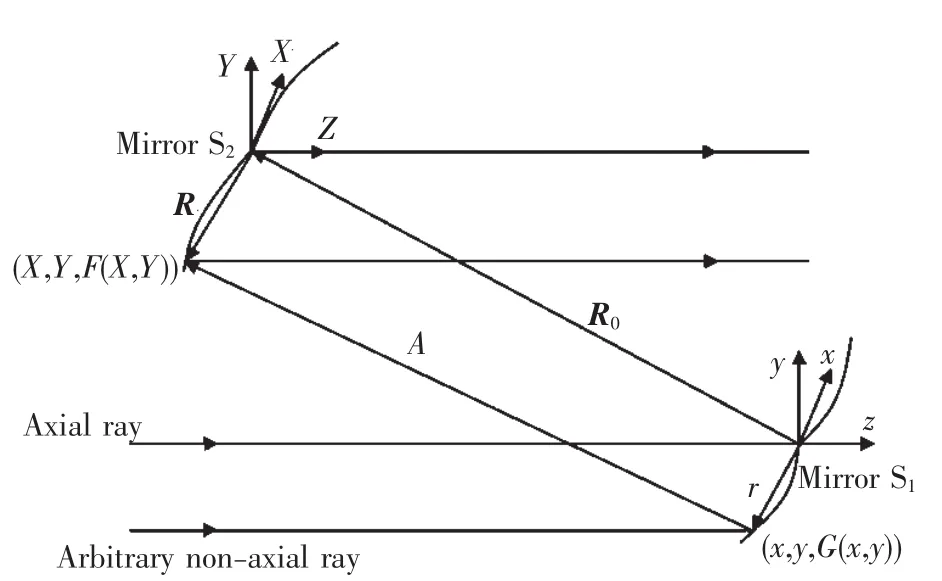
圖2 反射鏡面形計算原理圖Fig.2 Principle of calculating reflective surfaces

反射式激光光束整形系統的面形方程推導過程與折射式整形系統[8]相似，區別僅在于采用矢量形式的反射定律進行光線追跡[14-15]。圖2為反射式光束整形系統面形計算原理圖，反射鏡S1和反射鏡S2的面形分別在局部坐標系(x，y，z)和(X，Y，Z)中描述，兩局部坐標系均以對應反射鏡的軸上中心為原點，面形方程分別為z=G(x，y)和 Z=F(X，Y);設局部坐標系(X，Y，Z)的原點在局部坐標系(x，y，z)中的坐標為(X0，Y0，Z0)，因此軸上光線從反射鏡S1中心反射到反射鏡S2中心的矢量R0=(X0，Y0，Z0);任意軸外光線在反射鏡 S1上的入射點為(x，y，G(x，y))，反射光線單位矢量為A，在反射鏡S2上的入射點為(X，Y，F(X，Y))。

因為假設入射光線和出射光線均平行于光軸，為確保輸入輸出波前均為平面波，引入等光程條件[15]，即軸上光線在輸入輸出面之間經過的光程等于任意軸外光線在輸入輸出面之間經過的光程。根據等光程條件可以推得:2

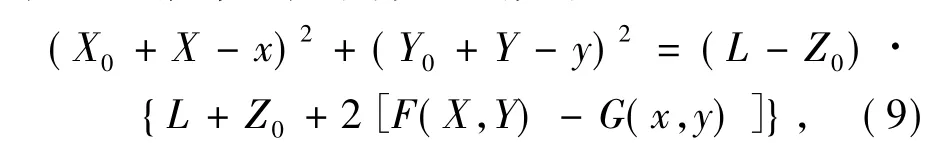
利用矢量形式的反射定律[15]并代入等光程條件可以得到G(x，y)對x和y的偏導Gx'和 G'y為:

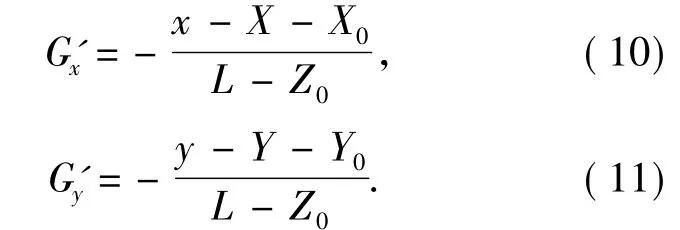
由于已將入射面橢圓方程轉化為r0和θ的函數，因此，需求出以r0和θ為自變量的反射鏡S1的面形方程G(r0，θ)。設兩反射鏡的中心在同一y-z平面內，則 X0=0。根據 x=rcosθ，y=rsinθ，X= ρcosφ，Y= ρsinφ 可求出 G(r，θ)對 r和θ的偏導，聯立式(5)可求出 G(r0，θ)對 r0和 θ的偏導為

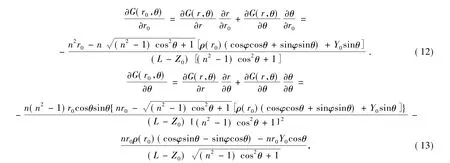
最后通過積分可求得G(r0，θ)為

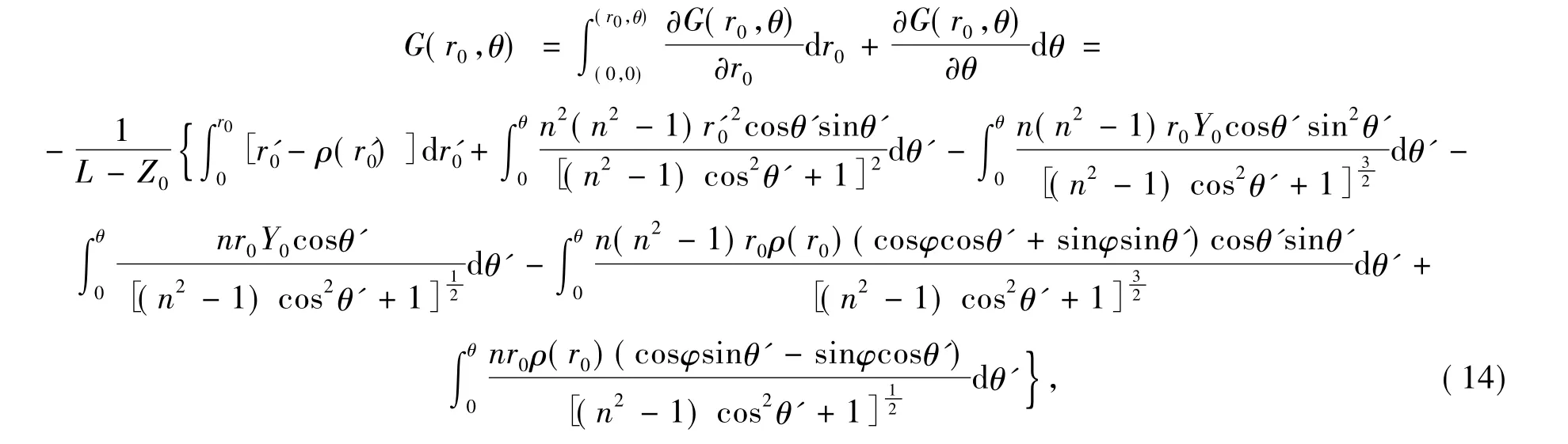
通過式(12)可推出 F(ρ，φ)和 G(r0，θ)的關系式為

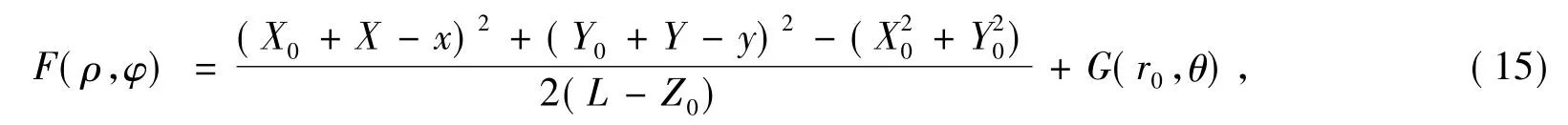
將 x=rcosθ，y=rsinθ，X=ρcosφ，Y=ρsinφ 以及式(5)代入上式可得

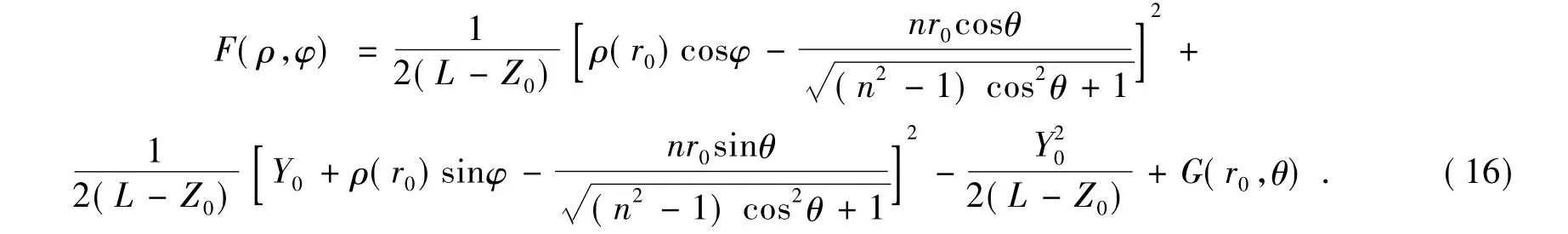
所求得的面形方程為積分形式，在MATLAB等數值計算軟件中有自帶函數可以調用，相比起二階非線性偏微分方程組，簡化了數值計算步驟。在求解時，首先給定入射光束各點坐標值(r0，θ)，通過坐標關系式(8)，利用 MATLAB軟件求出入射光束各點在出射面對應點的坐標值(ρ，φ)的數值解，然后一起代入式(14)、(16)求出兩面形方程的數值解。以上推導的坐標關系式(8)和反射鏡面形方程 (14)、(16)亦適用于對圓形高斯光束平頂整形，此時只需取m=n=1即可。

3 數值仿真

以美國GAM LASER公司的EX5/250 ArF準分子激光器為例，設計與其適用的反射式橢圓高斯光束整形器。EX5/250 ArF準分子激光器在水平方向上的光束尺寸為3 mm，束腰半徑ωx0=0.75 mm，FWHMx為 1 mrad;在豎直方向上的光束尺寸為6 mm，束腰半徑ωy0=1.5 mm，FWHMy為2 mrad，可取m=n=2;對以勻化洛倫茲函數表示的出射平頂光束，取RFL=3 mm，q=50。反射鏡S2相對于反射鏡S1的位置坐標(X0，Y0，Z0)=(0，10，－20)，長度單位為 mm。

利用MATLAB軟件采用數值解法求解面形方程，首先求解第一面反射鏡面形數據，在x-y面上選擇包含入射光束最大橢圓邊界的矩形區域，并對矩形區域進行離散，離散間隔分別為xi和yi，離散點為(xn，yn)，這些點對應的矢高值便是要求的第一面反射鏡的面形數據。然后，求出離散點(xn，yn)對應的極坐標形式(rn，θn)，再利用式(5)求出與(rn，θn)對應的(r0n，θn)，此時 x-y 面各點已化為(r0n，θn)的形式以代表各條光束入射點。利用式(8)求出出射面上與(r0n，θn)對應的坐標(ρn，φn)，并將(r0n，θn)和(ρn，φn)代入式(14)，使用MATLAB中自帶的積分函數quadl函數計算出矢高值 G(r0n，θn)。

使用光學軟件ZEMAX進行模擬，選擇grid sag面形，基準面為平面，使用線性插值。由于grid sag面形格式要求對輸入的面進行單獨離散，在計算第二面反射鏡面形數據時，需重新編程對出射面進行離散，離散點為(Xn，Yn)，求出其對應的極坐標形式(ρn，φn)，再根據式(8)計算出入射面對應的坐標(r0n，θn)。之后的運算與計算第一面反射鏡面形數據時相同，計算出G(r0n，θn)，最后再利用式(15)求解出 F(ρn，φn)。

第2節的理論分析是以入射光束發散角為0°為前提，為了增加仿真的精確性，在數值計算時計算入射光束發散角為0°時的面形數據，然后在光學軟件中加入角度進行仿真。可得到整形系統如圖3所示，光線追跡結果如圖4所示。可以看出較小的入射光束發散角對該系統的整形效果基本沒有影響。

選取光束出射方向上距離反射鏡S220 mm處作為目標面，以下式定義目標面照度均勻性P為

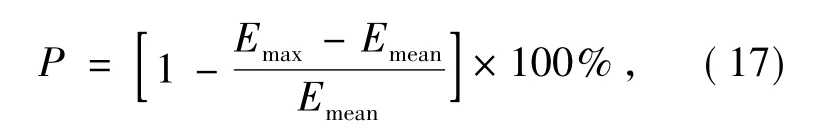
其中Emax為目標區域內的最大照度值，Emean為目標區域內的平均照度值。取半徑為2.84 mm的圓域作為目標區域，計算得到在目標區域內照度均勻性為95.45%;利用式(2)和式(17)，可求得理想出射光束在目標區域內的均勻性為99.86%;實際值與理想值之間的差別主要由于加入發散角追跡光線和光學軟件對于離散面形數據的插值誤差而引起的。

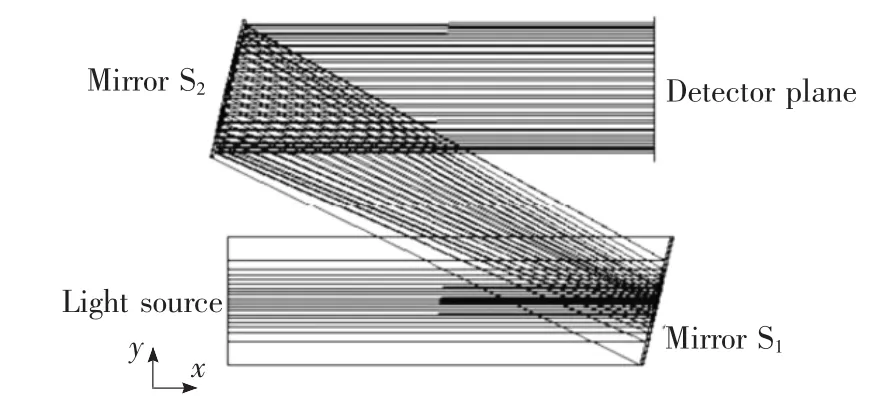
圖3 反射式橢圓高斯光束整形系統y-z平面的光線追跡圖Fig.3 Ray trace in y-z plane of the reflective elliptical Gaussian beam shaping system

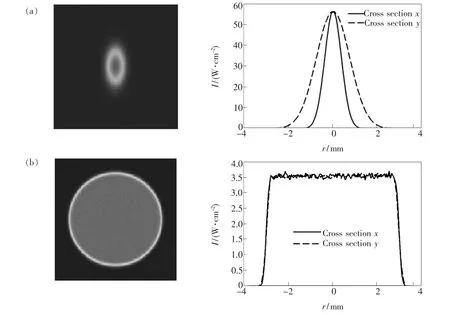
圖4 ZEMAX非序列光線追跡結果。Fig.4 Results of non-sequential ray tracing in ZEMAX.

4 系統分析

假設過S1中心的切平面為u-v平面，以該面為基準面分析反射鏡S1的面形隨參數Y0和Z0的變化規律。首先固定 Z0=20 mm，改變 Y0，反射鏡S1在正交方向上的輪廓曲線S1(u，0)和S1(0，v)的變化如圖5(a)所示;固定Y0=10 mm，改變Z0，反射鏡 S1在正交方向上的輪廓曲線S1(u，0)和 S1(0，v)的變化如圖 5(b)所示;等比例增大Y0和Z0，反射鏡S1在正交方向上的輪廓曲線S1(u，0)和S1(0，v)的變化如圖5(c)所示。

綜合圖5(a)、(b)、(c)可知，單獨增加 Z0和等比例增加Y0、Z0時，反射鏡S1在u和v方向上面形斜率同時變緩，可在一定程度上降低加工難度，且S1在u方向上的面形深度要比在v方向上的面形深度大一個數量級。用同樣的方法分析反射鏡S2，發現S2的面形隨參數Y0和Z0的變化規律與反射鏡S1相同。此外可以看出設計的反射鏡面形為非回轉對稱曲面，相比傳統回轉對稱的球面鏡和非球面鏡增加了加工難度。以超精密單點金剛石車削技術、流體輔助光學加工等為代表的先進光學制造技術發展迅速，使得加工高精度非回轉對稱光學曲面成為現實，目前采用飛刀銑削、快刀伺服車削和慢刀伺服車削技術均能加工復雜光學曲面。本文設計的非回轉對稱反射鏡關于橫、縱坐標軸對稱，在一定程度上降低了加工檢測難度。

圖5 反射鏡S1正交方向剖面輪廓與Y0、Z0關系圖。Fig.5 Relationships between surface profile of S1in cross section and Y0，Z0.

固定的橢圓高斯光束平頂整形器只針對特定的束腰大小使用，當束腰大小改變時，出射光束的平頂性也隨之改變。保持n=2，改變橢圓高斯光束在快慢軸上的束腰大小，出射光束光強輪廓如圖6所示。當入射光束束腰偏差在±0.05 mm時，出射光束均勻性降低到83%;當入射光束束腰偏差在±0.1 mm時，對出射光束平頂性的影響已經非常嚴重。因此，在使用橢圓高斯光束平頂整形器時，應確保入射光束束腰大小與整形器相匹配。

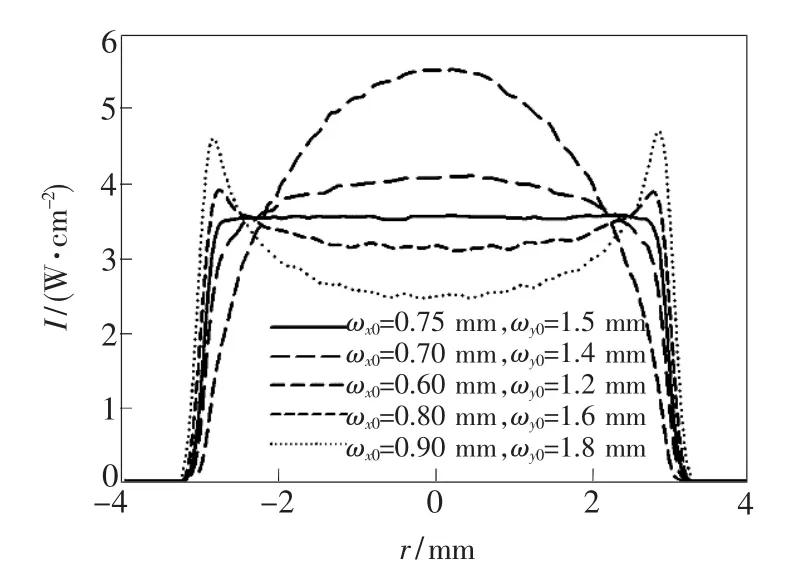
圖6 出射光束平頂性與入射光束束腰偏差關系圖Fig.6 Relationship between the uniformity and the incident beam waist deviation

反射鏡的面形誤差直接影響著系統的整形結果。分析系統面形誤差時，我們對通過式(8)、(14)、(16)計算出的有限個點的數值解加入正態分布的誤差值[17]，利用ZEMAX非序列進行幾何光線追跡，分析系統面形誤差對整形效果的影響。圖7為引入的均方根誤差值對光束出射方向上距離反射鏡S220 mm處的目標面上輻照度均勻性的影響。由圖可知，目標面上的輻照度均勻性在均方根誤差值不大于1 μm時在95%左右，當均方根誤差值大于1 μm時，輻照度均勻性快速降低。考慮到反射式整形系統更適合用于高功率激光器，為提高反射鏡表面抗激光損傷閾值，反射鏡的面形加工誤差應該更低。

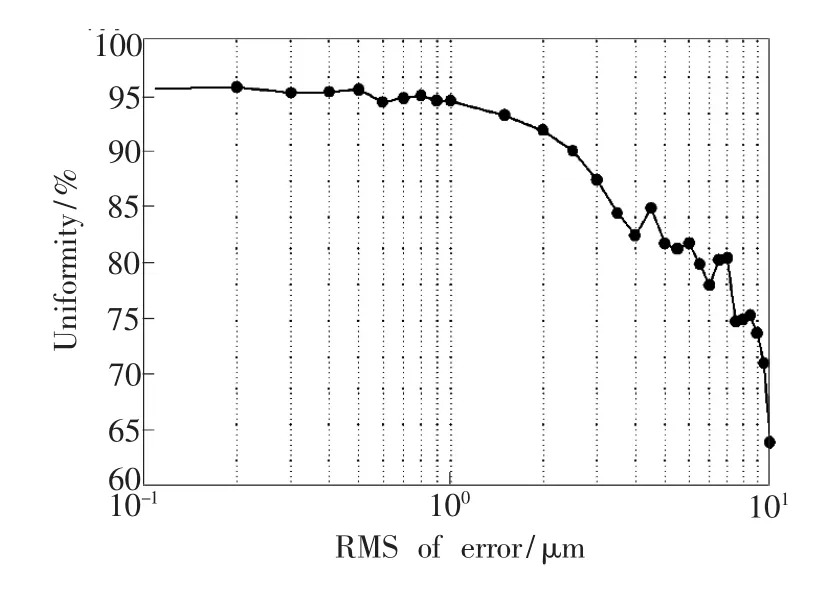
圖7 出射光束均勻性與面形均方根誤差關系圖。Fig.7 Relationship between the uniformity and the RMS of surface error

5 結 論

提出了一種將橢圓高斯光束轉化為圓形平頂光束的整形方法。為了同時適用于各波段和高功率情況，采用了無中心遮攔反射式結構，利用能量守恒和矢量形式的反射定律推導了同時適用于橢圓高斯光束和圓形高斯光束整形的坐標關系和面形方程，并給出了設計實例。從面形加工難度和輸出光束平頂性兩方面對系統進行了分析，認為增加兩反射鏡的水平距離和等比例增加水平和豎直距離有利于降低反射鏡的加工難度。該整形系統對入射光束尺寸要求嚴格，但對于面形加工精度要求較低。

[1]Zhao Y，Gong Y.Design of beam shaping unit for deep ultraviolet lithographic illumination system[J].Opt.Precision Eng.(光學 精密工程)，2011，19(1):29-34(in Chinese).

[2]Liu H，Liu B Y，Bai Y L，et al.Design of arbitrary waveform generator for shaping high power laser system[J].Chinese Optics(中國光學)，2011，4(1):60-65(in Chinese).

[3]Zhang Z J，Liu Y，Miao G Q，et al.The 2 kW semiconductor laser processing light[J].Chin.J.Lumin.(發光學報)，2013，34(3):334-339(in Chinese).

[4]Wang P C，Deng Y L，Zhang L P，et al.High brightness fiber coupled diode laser module[J].Chin.J.Lumin.(發光學報)，2012，33(12):1335-1341(in Chinese).

[5]Hao M M，Zhu H B，Qin L，et al.Research on high brightness fiber coupled diode laser module with hundred watts class output power[J].Chin.J.Lumin.(發光學報)，2012，33(6):651-659(in Chinese).

[6]Xie J J，Gao F，Pan Q K，et al.Laser mask micromachining system based on beam-scanning widening techningue[J].Chin.Opt.(中國光學)，2011，4(6):654-659(in Chinese).

[7]Ma J S，Xia F P，Su P，et al.Survey on key techniques and systems of digital holographic 3D display[J].Opt.Precision Eng.(光學 精密工程)，2012，20(5):1141-1152(in Chinese).

[8]Chang Y H，Ishii Y，Murata K.Reshaping collimated laser beams with Gaussian profile to uniform profile[J].Appl.Opt.，1983，22(22):3644-3647.

[9]Yu X C，Hu J S，Wang L B，et al.Laser beam shaping based on liquid-crystal spatial light modulator[J].Acta Optica Sinica(光學學報)，2012，32(5):0514001-1-5(in Chinese).

[10]Yang X T，Fan W.Spatial laser beam shaping using birefringent lenses[J].Acta Optica Sinica(光學學報)，2006，26(11):1698-1704(in Chinese).

[11]Frieden B R.Lossless conversion of a plane laser wave to a plane wave of uniform irradiance[J].Appl.Opt.，1965，4(11):1400-1403.

[12]Hoffnagle J A，Jefferson C M.Design and performance of a refractive optical system that converts Gaussian to a flattop beam [J].Appl.Opt.，2000，39(30):5488-5499.

[13]Zhang S，Neil G，Shinn M.Single-element laser beam shaper for uniform flat-top profiles[J].Opt.Exp.，2003，11(16):1942-1948.

[14]Malyak P W.Two-mirror unobscured optical system for reshaping the irradiance distribution of a laser beam[J].Appl.Opt.，1992，31(22):4377-4383.

[15]Shealy D L，Chao S H.Geometric optics-based design of laser beam shapers[J].Opt.Eng.，2003，42(11):3123-3138.

[16]Oliker V.Optical design of freeform two-mirror beam-shaping systems[J].J.Opt.Soc.Am.A，2007，24(12):3741-3752.

[17]Shang J L，Zhu X，Chen P，et al.Refractive optical reshaper that converts a laser Gaussian beam to a flat-top beam[J].Chin.J.Lasers(中國激光)，2010，37(10):2543-2549(in Chinese).