亞波長金屬光柵結構的制備與矢量衍射理論分析

鄭改革，詹 煜，曹 焜，徐林華

(南京信息大學物理與光電工程學院，江蘇南京 210044)

1 引 言

隨著光柵電磁理論研究的不斷深入和微加工技術的不斷進步，研究人員逐漸發現亞波長金屬光柵表現出了很多奇異的光學現象，比如介質層上的亞波長金屬光柵產生的表面等離子體(Surface Plasmon)可以極大地增強光柵下介質層內的透射光強[1-3]，亞波長金屬光柵能夠同時實現TE偏振(電矢量平行于光柵刻槽)的高反射和TM偏振(電矢量垂直于光柵刻槽)的高透射[3]等。目前，光柵的標量衍射理論已較為成熟，但它只適用于表面結構特征尺寸遠大于入射波長的光學元件。當光學元件的特征尺寸小至波長或亞波長量級時，基于標量衍射理論的框架進行二元光學器件的設計將缺乏可靠性，而需要采用電磁矢量衍射理論來分析研究光柵的衍射特性。

亞波長金屬光柵是一種特殊的光柵類型，而高深寬比(High Aspect Ratio，HAR)結構是其中比較典型的一類，其在生物傳感器、太陽能電池、超衍射光學光刻技術、近場光學成像等領域都有大量的應用[4-7]。高深寬比金屬結構的加工是目前微機電系統(MEMS)研究的熱點與難點之一。金屬器件在耐高溫、高壓以及在苛刻環境下的使用比硅基器件具有明顯的優勢，但由于目前金屬結構加工手段的欠缺，截止到目前絕大多數MEMS器件依然以硅基微加工技術為主。

本文利用納米壓印技術結合濺射和反應離子刻蝕工藝制備了深寬比達到4∶1的亞波長金屬光柵，使用紫外可見近紅外光譜儀測得了光柵的反射光譜。根據參考文獻[8]提供的方法，在傳統的嚴格耦合波理論的基礎上，把光柵區域電磁場的空間諧波通過勒讓德多項式展開，求解光波在亞波長光柵體內的場分布。比較發現，實驗測量同理論分析結果在共振波長處吻合得很好。當光柵的深寬比增加時，在反射光譜中會觀察到更多的谷值，我們分析了其產生的原因。

2 光柵的矢量衍射理論分析

分析如圖1所示的亞波長光柵。區域1的介電常數為ε1，區域3的介電常數為 ε3，中間為介電常數受到周期性調制的光柵區。光柵平面的法線方向沿z軸，光柵矢量沿x軸。光柵周期為Λ，占空比為f，光柵深度為h。光柵區域(0＜z＜h)包含了兩種介質的周期分布，其介電系數為一周期函數，對應的介電常數表示為ε(x+Λ)=ε(x)。

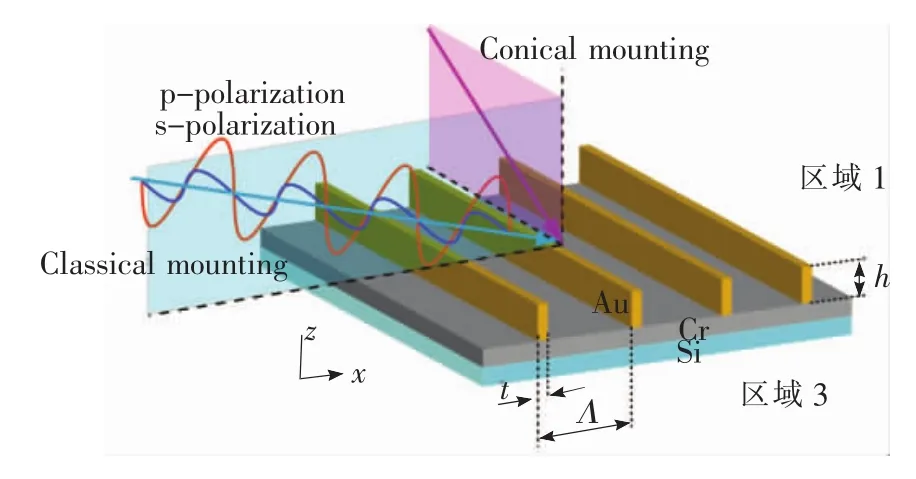
圖1 亞波長金屬光柵基本結構Fig.1 The basic structure of subwavelength metallic grating

嚴格耦合波分析(Rigorous Coupled Wave Analysis)[8-9]方法由于計算簡單快捷，被廣泛應用于各種周期性結構衍射體的電磁場衍射的分析中，但其沒有充分考慮光柵介質以及電磁波在光柵矢量方向上的邊界最佳匹配條件，在求解本征矩陣方程時，計算結果往往收斂很慢，有時甚至出現數值溢出，導致病態矩陣。這種情況對于TM波尤為突出。衍射波由傳播波和倏逝波組成，對于遠場衍射，倏逝波在到達遠場前就已衰減為0，因此對遠場衍射的貢獻主要是傳播波。但分析表面等離激元極其相關的亞波長光學現象時，涉及的往往都是TM波而且是近場情形，尤其是存在倏逝波的情形，所以為了更深刻的分析亞波長金屬光柵的衍射特性，有必要對耦合波分析方法做一定的修正。

我們利用文獻[8]的方法，在傳統的嚴格耦合波理論的基礎上，先是采用快速傅立葉因式分解(FFF)的方法求得TM偏振光入射下的耦合波方程，再把光柵區域電磁場的空間諧波通過勒讓德多項式展開[10]，避免了病態矩陣的出現，不僅可以用于分析衍射特性，還能很方便地求解光波在亞波長光柵體內的場分布。修正的適用于亞波長光柵的耦合波分析理論按照如下步驟進行求解:

(1)將光柵區域劃分成若干個水平層;

(2)在每一分層中利用快速傅立葉因式分解方法構建耦合波方程，將電磁場空間諧波按勒讓德多項式展開;

(3)逐層應用電場和磁場邊界連續條件，將各個分層的電場磁通過耦合波方程聯系起來;

(4)求解反射和透射的衍射波振幅，將其帶到空間諧波方程就可求得光柵體內的光場分布。

由于數值計算只能進行有限項運算，因此在計算時必須對求和項進行截斷，這不可避免地會給計算結果帶來截斷誤差。求和子波項數越多，截斷誤差越小，計算精度越高;但是子波數越多，計算工作量也越大。所以在計算時應在保證計算精度的前提下，減小計算工作量，提高計算速度。在我們的計算中選取勒讓德多項式展開的項數為10，空間諧波數為6。數值計算結果表明，這兩個參數能夠使我們獲得足夠準確的解，保證了收斂性。

3 亞波長光柵的制備與光譜響應測量

為了在硅片上制備出金光柵結構，我們首先在經過清潔處理的硅片上用電子束蒸發鍍上鉻層起黏附作用，再旋涂環烯烴聚合物(COP)薄膜。在50 W條件下蒸鍍7 min，得到的鉻層厚度約為120 nm。接著將環烯烴聚合物(COP)薄膜旋涂在充分清洗的硅片襯底上。COP的透射率為92%，折射率為1.509，熱形變溫度為123℃。在旋涂過程中要用高于3 000 r/min的轉速，保證旋涂出均勻的膜層。使用 SCIVAX、X-200型納米壓印機，在1 000 N壓力、150℃條件下壓印120 s，結束后將襯底溫度冷卻到50℃，以10 μm/s的速度將壓印模板與襯底直接脫模分離。利用Anelva E-200S濺射系統在制備出的光柵結構上鍍Au薄膜120 s，得到的薄膜厚度為200 nm。然后利用反應離子刻蝕機(Samco-10NR型)對納米復合結構進行刻蝕。用Ar和CF4混合氣體在室溫下刻蝕上表面的金6 min。用氧反應離子刻蝕(O2RIE)殘留的COP層。在氣體流速為50 cm3/min、射頻功率為100 W、反應時壓力為10 Pa的刻蝕參數下，刻蝕速率可穩定在200 nm/min。最后用氯苯、丙酮溶液超聲清洗掉光刻膠，就會在硅片上留下需要制備的金光柵結構，周期為1 μm、占空比為0.2。亞波長金屬光柵的AFM和SEM照片如圖2所示。

圖2 亞波長金屬光柵的AFM和SEM照片。Fig.2 The AFM and SEM images of the fabricated subwave-length metallic gratings.

在一束TM偏振光以20°入射的情況下，我們使用紫外-可見-近紅外光譜儀(V-670:JASCO，Tokyo，Japan)測量了0級反射光譜，結果見圖3(b)，使用修正矢量衍射理論計算得到的反射譜在圖中用虛線畫出。在數值計算和理論分析中，對于金屬，它們的介電常數的色散和吸收是不能忽略的。金和鉻是最典型的Drude金屬，其介電常數可用Drude模型來很好地近似。本文取對于金，等離子體頻率ωp=8.99 eV，電子的弛豫時間(ωpτ)－1=0.026 78[11]。對于鉻，等離子體頻率 ωp=4.6 eV，電子的弛豫時間(ωpτ)－1=0.225[11]。

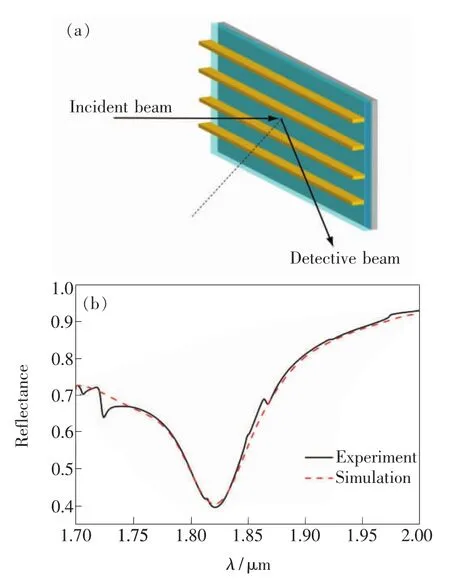
圖3 (a)反射光譜測量系統的簡單示意圖;(b)測量得到的0級反射譜。Fig.3 (a)Schematic diagram of the experimental setup used to measure the grating refiectance spectra.(b)The calculated and measured zero-order reflectance spectra in air.

數值計算所選的參數都與實驗制備的樣品參數一致。光柵周期為1 μm，金的高度為800 nm，寬度為200 nm，基底材料是Si，在Si上覆蓋一層厚度為160 nm 的鉻。波長為1.82 μm 和2 μm的TM偏振光以20°入射到光柵表面，計算得到的磁場Hy分布如圖4所示。可以看出，我們提出的修正矢量衍射理論可以方便地求解出亞波長光子器件內的電磁波傳輸特性。同時揭示了以矩形金屬為單元的金屬光柵表面的共振模式存在兩種情況:一種是水平方向的SPR，存在于金屬上下表面，是一種水平周期結構引發的共振;另一種存在于金屬左右垂直表面的微腔諧振模式。

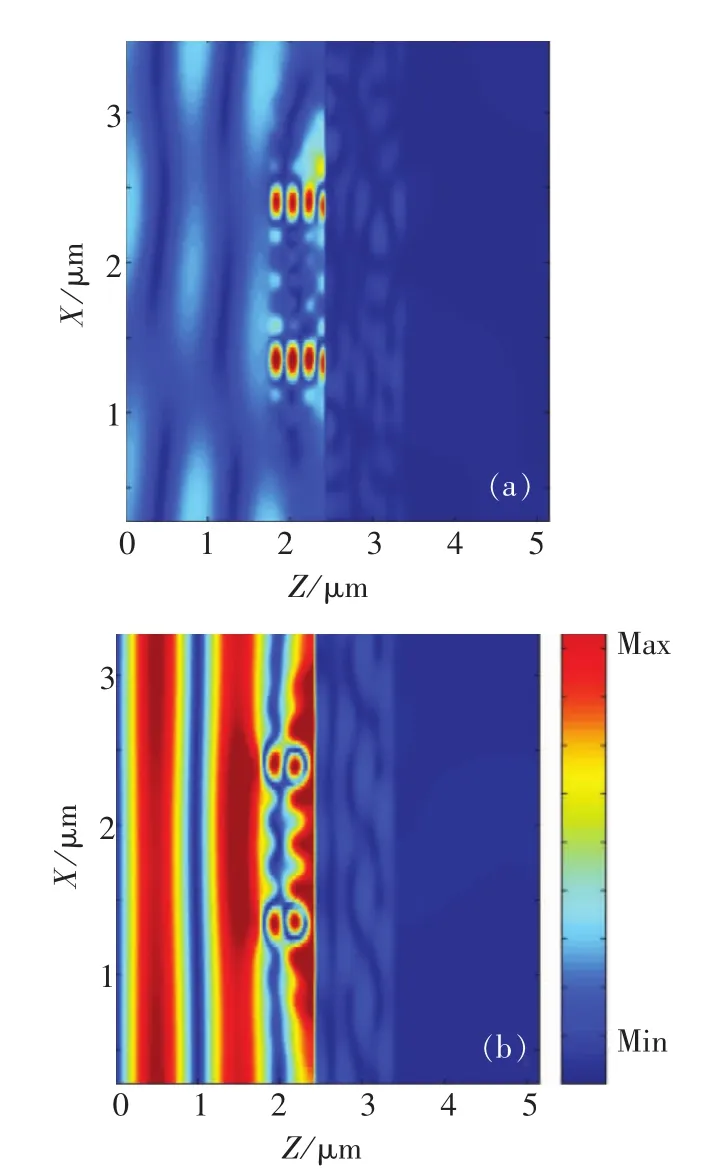
圖4 使用修正矢量衍射分析方法計算得到兩種波長對應的磁場分布。Fig.4 The calculated field distribution based on vector diffraction theory.

當入射光束照射到光柵表面時，將產生一系列的衍射光波，當某一級衍射光光波矢在界面方向上的分量與表面等離子體波的波矢相匹配時，二者發生共振，該級次的衍射光波的強度會急劇下降，即產生表面等離子體共振現象。圖5為反射譜隨光波長和入射角度之間的關系。根據光柵理論，SP共振條件為:

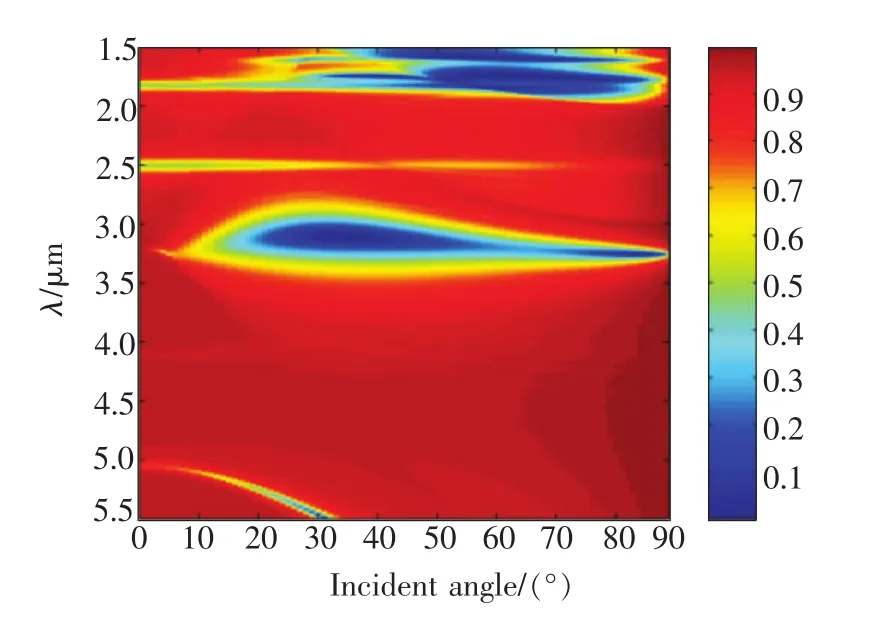
圖5 反射譜隨光波長和入射角度的變化Fig.5 Reflectance variation with the incident light wavelength and the incident angle

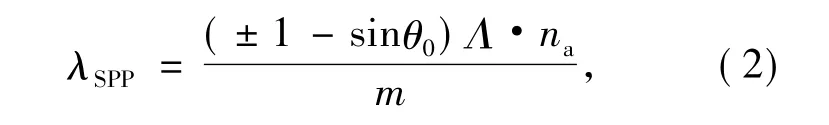
其中λSPP代表表面等離子體共振波長，θ0代表光波入射角度。當待測物質折射率(na)發生改變時，不同衍射級次光波對應的共振波長也會隨之變化。研究表明，表面等離子共振條件對于金屬表面介質折射率的微小變化非常敏感。因此，當金屬表面的介質為一種待測分析物時，則可以通過記錄共振角或共振波長的變化來實現對待測分析物折射率的檢測，這就是SPR傳感器的工作原理。當折射率增加時，正級次衍射光波對應的共振波長增大，而負衍射級次衍射光波對應的共振波長在減小。當待測物質折射率變化量相同時，可以看出，負級次衍射光波對應的共振波長變化量大于正衍射級次光波。

圖6 入射光垂直入射到不同深寬比光柵對應的反射光譜Fig.6 The calculated reflectance spectra for gratings with different aspect ratios

當入射光垂直入射到具有不同深寬比的光柵表面時，計算得到的反射譜線如圖6所示。對比發現，深寬比為10∶1的光柵的光譜會出現更多的反射谷，這是由于當光柵的深度增加，當入射光波長滿足一定關系時，會在光柵槽中形成微腔諧振模式，這是一種類 Fabry-Perot共振模式。根據F-P腔諧振公式:

式中neff為對稱金屬包裹介質波導模型的有效折射率，λ為入射光波長，m為整數。這種微腔諧振模式對金屬光柵的異常透射和光耦合增強均會產生作用，引起了很多研究者的關注[1，12]。

矢量衍射分析方法為研究亞波長尺度下的光傳輸問題提供了一種技術手段。由于表面等離子激元局限在金屬和電介質的表面處，其透射增強作用僅作用于數百納米的近場，這與傳統的透射光柵有所區別。嚴格耦合波理論的優勢在于對于無論何種形狀的納米結構，只要其折射率分布具有周期性，我們都可以快捷的求出衍射效率和光場分布，不像有限差分法那樣需要考慮結構的尺寸大小，很難處理大尺寸結構。

4 結 論

使用納米壓印技術結合濺射和反應離子刻蝕工藝制備了一種金屬光柵，并使用紫外-可見-近紅外光譜儀測量了光柵的反射光譜。根據參考文獻[8]提供的方法，在嚴格耦合波理論的基礎上，把光柵區域電磁場的空間諧波通過勒讓德多項式展開，通過求解光波在亞波長光柵體內的場分布，得到光柵的反射光譜。同實驗測量結果對比發現，修正的矢量衍射分析方法精確地求得了光柵反射光譜的共振波長位置，驗證了其分析亞波長光柵的可行性。數值計算結果表明，以矩形金屬為單元的金屬光柵表面的共振模式存在兩種情況:一種是水平方向的SPR，存在于金屬上下表面，是一種水平周期結構引發的共振;另一種存在于金屬左右垂直表面的微腔諧振模式，這是一種類Fabry-Perot共振模式。本文的研究結果為進一步探索亞波長金屬光柵在生物傳感、薄膜太陽能電池等領域的應用提供了一定的參考。

[1]Bai W L，Guo B S，Cai L K，et al.Simulation of light coupling enhancement and localization of transmission field via subwavelength metallic gratings[J].Acta Phys.Sinica(物理學報)，2009，58(11):8021-8026(in Chinese).

[2]Yang Z L，Fang W J，Yang Y Q.Two-photon-excited fluorescence enhancement caused by surface plasmon enhanced exciting light[J].Chin.J.Lumin.(發光學報)，2013，34(2):240-244(in Chinese).

[3]Han J，Fan Y C，Zhang Z R.Propagation of surface plasmon polaritons in a ring resonator with PT-symmetry[J].Chin.J.Lumin.(發光學報)，2012，33(8):901-904(in Chinese).

[4]Dinesh A，Sumet H，Prashant T，et al.Fabrication of compliant high aspect ratio silicon microelectrode arrays using micro-wire electrical discharge machining[J].Microsyst.Technol.，2009，15:789-797.

[5]Zhang X W，Ning Y Q，Qin L，et al.Polarization control of 980 nm high-power vertical-cavity surface-emitting lasers by using sub-wavelength metal-gratings[J].Chin.J.Lumin.(發光學報)，2012，33(9):1012-1017(in Chinese).

[6]Xiao X X，Chen Y G.Investigation of optical wave coupling between two subwavelengh slits in metallic sheet[J].Chin.J.Lumin.(發光學報)，2009，30(5):682-686(in Chinese).

[7]Liu J，Liu J，Wang Y T，et al.Resonant properties of sub-wavelength metallic gratings[J].Chin.Opt.(中國光學)，2011，4(4):363-368(in Chinese).

[8]Moharam M G，Gaylord T K.Rigorous coupled-wave analysis of planar-grating diffraction[J].J.Opt.Soc.Am.A，1981，71(7):811-817.

[9]Hooper I R，Sambles J R.Coupled surface plasmon polaritons on thin metal slabs corrugated on both surfaces[J].Phys.Rev.B，2004，70(4):045421-1-14.

[10]Khavasi A，Jahromi A K，Mehrany K.Longitudinal Legendre polynomial expansion of electromagnetic fields for analysis of arbitrary-shaped gratings[J].J.Opt.Soc.Am.A，2008，25(7):1564-1573.

[11]Lynch D W.Hunter W R.Handbook of Optical Constants of Solids[M].London:Academic Press，1985:286-287.

[12]Wang Y W，Liu M L，Liu R J，et al.Fabry-Perot resonance on extraordinary transmission through one-dimensional metallic gratings with sub-wavelength under transverse electric wave excitation[J].Acta Phys.Sinica(物理學報)，2011，60(2):024217(in Chinese).