一類半無限規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)算法

昌吉學(xué)院 數(shù)學(xué)系，新疆 昌吉 831100

昌吉學(xué)院 數(shù)學(xué)系，新疆 昌吉 831100

半無限凸規(guī)劃的一般形式為：

其中 x=(x1，x2，…，xn)T∈Rn，A∈Rm×n(m≤n)，b∈Rm。 g和fi(i∈I)是 Rn上的凸函數(shù)，I為無限集。為求解問題（1），作如下假設(shè)：問題（1）存在有限解x*∈Rn。

半無限規(guī)劃問題是數(shù)學(xué)規(guī)劃的一個(gè)重要分支。它應(yīng)用于許多領(lǐng)域，如控制系統(tǒng)設(shè)計(jì)、分散系統(tǒng)的資源配置、信號(hào)處理中的濾波器設(shè)計(jì)等。此外隨著近代工業(yè)技術(shù)的快速發(fā)展，由于要不斷提高對(duì)產(chǎn)品性能的期望，還要受到環(huán)境和資源等條件的諸多限制，使得許多實(shí)際問題都可以建立成半無限規(guī)劃的數(shù)學(xué)模型。所以研究半無限規(guī)劃問題就顯得很重要。但是在半無限規(guī)劃問題中，由于其約束條件的個(gè)數(shù)是無限的，這就給數(shù)值求解帶來比較大的困難，使現(xiàn)有的許多算法都比較復(fù)雜，而且不容易被人們所掌握。所以如何求解半無限規(guī)劃問題就具有非常重要的實(shí)際價(jià)值和理論意義。目前，在很多科學(xué)技術(shù)和工程領(lǐng)域，經(jīng)常需要實(shí)時(shí)求解（1）。然而基于電路實(shí)現(xiàn)的神經(jīng)網(wǎng)絡(luò)，具有大規(guī)模并行處理，分布式存儲(chǔ)和高度的糾錯(cuò)能力等許多優(yōu)點(diǎn)，成為一些領(lǐng)域求解大規(guī)模優(yōu)化問題的有效方法。此外運(yùn)用神經(jīng)網(wǎng)絡(luò)求解優(yōu)化問題也已得到廣泛的研究，并取得較好成果[1-4]。基于上述考慮，為實(shí)時(shí)并行求解問題（1），本文根據(jù)其結(jié)構(gòu)特點(diǎn)，構(gòu)造了求解它的一個(gè)神經(jīng)網(wǎng)絡(luò)模型，并嚴(yán)格證明該神經(jīng)網(wǎng)絡(luò)模型是Lyapunov穩(wěn)定的，還收斂于問題（1）的精確解。數(shù)值實(shí)驗(yàn)表明該模型不僅是可行的，而且是有效的。為敘述方便，用‖·‖表示歐氏范數(shù)。

1 極大熵函數(shù)的提出及其性質(zhì)

對(duì)于半無限規(guī)劃問題（1），由于它的約束條件的個(gè)數(shù)是無限多的，不易于求解。文獻(xiàn)[5]中證明：當(dāng)所考慮問題是凸規(guī)劃時(shí)，可用下述問題（2）逼近問題（1）。即問題（1）的最優(yōu)解可以通過問題（2）的最優(yōu)解獲得。因此本文應(yīng)用極大熵方法，提出了求解問題（1）的一個(gè)神經(jīng)網(wǎng)絡(luò)模型。

考慮下述問題：

min g(x)

因此問題（1）的最優(yōu)解可由問題（3）的最優(yōu)解來逼近。

由于極大值函數(shù)F(x)是不可微的，則問題（3）就是不可微優(yōu)化問題。因此借助最大熵原理導(dǎo)出一族一致逼近F(x)的可微函數(shù)（稱之為熵函數(shù)），定義如下[6]：

其中 p＞0是控制參數(shù)。從而問題（3）可進(jìn)一步地轉(zhuǎn)化為如下光滑問題：

其中Fp(x)由式（4）定義。因此可以根據(jù)定理2，通過求解p充分大時(shí)的問題（5）的最優(yōu)解去逼近原問題的最優(yōu)解。

為應(yīng)用方便，下面介紹熵函數(shù)Fp(x)的一些性質(zhì)：

性質(zhì)1[7]若 fi(x)(i=1，2，…，l)都是凸函數(shù)時(shí)，則對(duì)?p＞0，F(xiàn)p(x)也是凸函數(shù)。

定理1[7]對(duì)?x∈Rn，p＞0，有：

定理2[7]當(dāng)x∈Rn，p→+∞時(shí)，F(xiàn)p(x)一致收斂于F(x)。

定理3[7]設(shè) x*是式（1）的解，xp是由極大熵函數(shù)法求的近似解，則有：

2 神經(jīng)網(wǎng)絡(luò)模型

為建立求解式（5）的神經(jīng)網(wǎng)絡(luò)，首先問題（5）滿足slater’s條件，即存在 x′∈Rn，使得：

作為構(gòu)建網(wǎng)絡(luò)的理論基礎(chǔ)，給出其解的充要條件：

定理4 x*是式（5）的最優(yōu)解當(dāng)且僅當(dāng)存在 λ*∈R，μ*∈Rm，使得：

證明顯然問題（5）的拉格朗日函數(shù)為：

它是定義在C=Rn×R×Rm。

由于問題（5）是凸的，且滿足Slater條件，根據(jù)凸規(guī)劃KKT條件知：x*是問題（5）的最優(yōu)解，當(dāng)且僅當(dāng)存在λ*∈R，μ*∈Rm，使得 (x*，λ*，μ*)是 L(x，λ，μ)在 C 上的鞍點(diǎn)，即

由式（7）左邊：

進(jìn)而對(duì) ?(λ，μ)∈R+×Rm，有：

再對(duì) ?x∈Rn，且 x≠x*，可知 x*+t(x-x*)∈Rn，?t∈(0，1)，那么由式（7）右邊得：

令t→0，并取極限，就有：

下面引入記號(hào)，標(biāo)記 z=(xT，λT，μT)T，z*=((x*)T，(λ*)T，(μ*)T)T∈Rn+m+1。

其中 F(z)是從Rn+m+1到Rn+m+1的連續(xù)映射，C是Rn+m+1上的非空閉凸子集，?g(x)是g(x)的梯度。于是定理4等價(jià)于如下定義的變分不等式VI(C，F(xiàn))：

又根據(jù)射影定理〔8〕和定理4，可進(jìn)一步推出如下結(jié)論：

引理1 x*是問題（5）的最優(yōu)解當(dāng)且僅當(dāng)存在 λ*∈R，μ*∈Rm，使得：

成立。

引理1說明通過求解系統(tǒng)（8）可以得到問題（5）的最優(yōu)解。為方便，記 λ~＝[λ-Fp(x)]+，根據(jù)以上分析和論述，可以得到求解（5）的神經(jīng)網(wǎng)絡(luò)，即

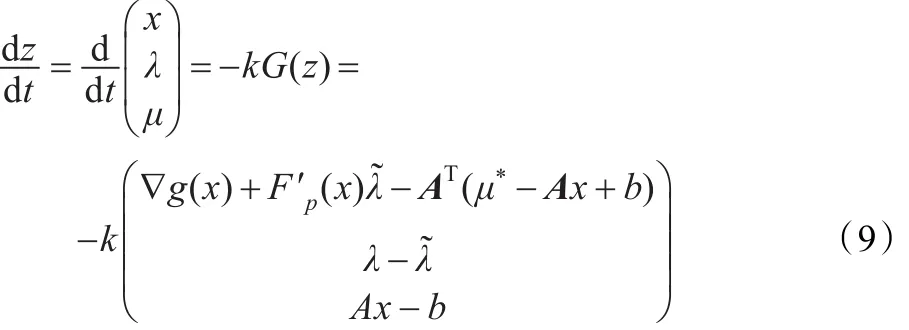
其中k＞0是設(shè)計(jì)參數(shù)。接下來根據(jù)引理1，可以得到如下關(guān)于式（8）的解和式（9）的平衡點(diǎn)這兩者之間的關(guān)系的結(jié)論，即

推論1 令 C*={z∈Rn+m+1|z是式（8）的解}，則 z∈C*當(dāng)且僅當(dāng)z是神經(jīng)網(wǎng)絡(luò)（9）的平衡點(diǎn)。

3 穩(wěn)定性分析

為了討論網(wǎng)絡(luò)（9）的動(dòng)力行為，先給出如下引理。

引理2 令 z*=((x*)T，λ*，(μ*)T)T∈ C*是有限的，則

定理5 若?g(x)、F′p(x)在 Rn上局部Lipschitz連續(xù)，則對(duì)任意的 z0∈Rn+m+1，神經(jīng)網(wǎng)絡(luò)（9）在 [0，+∞)上存在唯一的以 z0為初值的連續(xù)解 z(t)(z(t0)=z0，?t≥t0)(z(t)∈C*)。

類似文獻(xiàn)[9-10]中的證明，對(duì)網(wǎng)絡(luò)（9）有如下穩(wěn)定性結(jié)論。

定理6 若?g(x)、F′p(x)在 Rn上局部Lipschitz連續(xù)，則神經(jīng)網(wǎng)絡(luò)（9）是Lyapunov穩(wěn)定的。并且?z0∈Rn+m+1，對(duì)應(yīng)軌線z(t)(z(t0)=z0，?t≥t0)在有限時(shí)間內(nèi)收斂于C*中的一個(gè)點(diǎn)。特別地，若C*={z*}，則神經(jīng)網(wǎng)絡(luò)（8）全局漸近穩(wěn)定。

4 數(shù)值模擬

在pc機(jī)上對(duì)如下實(shí)例用ODE23模擬實(shí)驗(yàn)驗(yàn)證神經(jīng)網(wǎng)絡(luò)（9）的有效性和上章理論正確性。

例 考慮如下半無限規(guī)劃問題：

根據(jù)上一章的分析，

由極大熵函數(shù)法，問題（11）等價(jià)于：

其中 p＞0是控制參數(shù)。該問題有最優(yōu)解(x*)′=(-0.191 4，-1.277 3，1.729 2)。易知 (x*)′也是問題（10）的最優(yōu)解。

用神經(jīng)網(wǎng)絡(luò)（9）求解該問題。所有模擬結(jié)果表明，對(duì)于任意給定的初始點(diǎn)，神經(jīng)網(wǎng)絡(luò)（9）總收斂于該問題的精確解。例如，圖1顯示了k=500和任取30個(gè)初始點(diǎn)時(shí)網(wǎng)絡(luò)（9）的軌線性態(tài)。

圖1 k=500和任取30個(gè)初始點(diǎn)時(shí)網(wǎng)絡(luò)（9）的軌線性態(tài)1

其中 p＞0是控制參數(shù)。該問題有最優(yōu)解(x*)″=(-0.191 4，-1.277 7，1.729 7)。易知 (x*)″也是問題（10）的最優(yōu)解。

用神經(jīng)網(wǎng)絡(luò)（9）求解該問題。所有模擬結(jié)果表明，對(duì)于任意給定的初始點(diǎn)，神經(jīng)網(wǎng)絡(luò)（9）總收斂于該問題的精確解。例如，圖2顯示了k=500和任取30個(gè)初始點(diǎn)時(shí)網(wǎng)絡(luò)（9）的軌線性態(tài)。

圖2 k=500和任取30個(gè)初始點(diǎn)時(shí)網(wǎng)絡(luò)（9）的軌線性態(tài)2

其中 p＞0是控制參數(shù)。該問題有最優(yōu)解(x*)?=(-0.191 4，-1.277 5，1.729 4)。易知 (x*)?也是問題（10）的最優(yōu)解。

用神經(jīng)網(wǎng)絡(luò)（9）求解該問題。所有模擬結(jié)果表明，對(duì)于任意給定的初始點(diǎn)，神經(jīng)網(wǎng)絡(luò)（9）總收斂于該問題的精確解。例如，圖3顯示了k=500和任取30個(gè)初始點(diǎn)時(shí)網(wǎng)絡(luò)（9）的軌線性態(tài)。

圖3 k=500和任取30個(gè)初始點(diǎn)時(shí)網(wǎng)絡(luò)（9）的軌線性態(tài)3

5 結(jié)論

從上述過程可以看出，所提出的新模型不僅可行而且有效。

[1]Gao X B.A neural network for a class of extended linear variational inequaities[J].Chinese Journal of Electronics，2001，10（4）：471-475.

[2]Xia Y S.A new neural network for solving linear programming and quadratic programming problems[J].IEEE Trans on Neural Networks，1996，7：1544-1547.

[3]Xia Y S，Wang J.A general methodology for designing globally convergentoptimization neuralnetworks[J].IEEE Transon Neural Networks，1998，9：1311-1343.

[4]Bouzerdorm A，Pattison T R.Neural network for quadratic optimization with bound constraints[J].IEEE Trans on Neural Networks，1993，4：293-304.

[5]Karney D F.A pathological semi-infinite convex programs and their finite subprograms[J].Math Prog，1963，27：75-82.

[6]Kreisseloneier G，Steinhauser R.Systematic control design by optimizing a vector performance index[C]//Proc of IFAC Symp on CAD of Contor Sys，1979：113-117.

[7]李興斯.一類不可微優(yōu)化問題的有效解法[J].中國科學(xué)：A輯，1994，24（4）：371-377.

[8]Kinderlehrer D，Stampacchia G.An introduction to variational inequalities and applications[M].New York：Academic，1980.

[9]Gao X B，Liao L Z，Qi L Q.A novel neural network for variational inequalities with linear and nonlinear constraints[J]. IEEE Trans on Neural Network，2005，16（6）：1305-1317.

[10]Gao X B.A novel network for nonlinear convex programming[J].IEEE Trans on Neural Network，2004，15（3）：613-621.

一類半無限規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)算法

楊紅梅

YANG Hongmei

Department of Mathematics,College of Changji,Changji,Xinjiang 831100,China

The paper considers the semi-infinite problem with inequalities and equality constraints.By using maximal entropy method,it converts many constraints problem into single constraint nonlinear programming.Then it proposes a new neural network for solving it.It is shown to be Lyapnuov stable,and convergent to an exact solution of the problem in finite time.Illustrative examples show the feasibility and efficiency of the network.

semi-infinite convex programming;maximal entropy function method;neural network

考慮了一類帶有不等式和等式混合約束的半無限規(guī)劃問題。通過運(yùn)用極大熵方法，將多個(gè)約束條件的問題轉(zhuǎn)化為單個(gè)約束條件的非線性規(guī)劃模型，并提出了求解它的一個(gè)神經(jīng)網(wǎng)絡(luò)模型，嚴(yán)格證明了該模型是Lyapunov穩(wěn)定的，并且在有限時(shí)間內(nèi)收斂到原問題的一個(gè)精確解。數(shù)值實(shí)驗(yàn)表明，新模型不僅可行而且有效。

半無限凸規(guī)劃；極大熵函數(shù)法；神經(jīng)網(wǎng)絡(luò)

A

O221.2

10.3778/j.issn.1002-8331.1203-0551

YANG Hongmei.Neural network model for solving semi-infinite problem.Computer Engineering and Applications, 2013,49（11）：38-40.

昌吉學(xué)院科研基金（No.2010YJYB008）；昌吉學(xué)院運(yùn)籌學(xué)與最優(yōu)化研究群體（No.2011YJQT001）。

楊紅梅，女，講師，研究方向：神經(jīng)網(wǎng)絡(luò)、最優(yōu)化理論與算法。E-mail：20813524@qq.com

2012-03-23

2012-06-04

1002-8331（2013）11-0038-03

CNKI出版日期：2012-07-19 http://www.cnki.net/kcms/detail/11.2127.TP.20120719.1112.002.html