基于憶阻的自適應單神經元多變量解耦PID控制器

方曉燕，王麗丹，段書凱

(西南大學電子信息工程學院，重慶 400715)

目前，在工業控制中應用最廣泛的調節器控制規律為比例、積分、微分控制，即 PID控制［1］。PID控制器問世至今已有近70多年，因其結構簡單、穩定性好、工作可靠而成為最常用的工業控制器［2］。隨著工業控制中非線性、時變、強耦合、多變量和不穩定等多種復雜控制對象的出現［3］，對PID控制器的參數整定、結構設計、硬件實現、操作手段、適應能力等提出了更高的要求。因此，研究人員提出了基于單神經元、神經網絡、模糊［4－6］等的智能控制方法。

1971年，美籍華人科學家 Leon O.Chua教授［7－8］根據電路理論的完備性確定了電荷和磁通量之間的關系，定義了憶阻器，稱之為第4種基本電路元件。它是通過控制外加電壓(或電流)改變憶阻值實現參數的調整，使其本身可以作為滑動變阻器。同時，憶阻器是納米級元件具有更微小的體積，而且其本身的類突觸特性［9－10］使它可以代替神經網絡中的突觸權值。

本文利用憶阻器可以作為突觸的優勢，將此元件應用到PID控制網絡中，用憶阻器取代神經網絡中3個突觸權值，即單神經元網絡的比例、積分和微分系數。憶阻突觸權值的自動調節使PID控制網絡能適應環境的變化，實現多變量控制，滿足現代工業對時變、非線性、高控制品質和多變量復雜系統的控制需求，從而可構建基于憶阻的單神經元多變量解耦PID控制器。本文以兩變量解耦控制器為例。

1 單神經元自適應多變量解耦PID控制器

隨著科技的發展，控制系統變得越來越復雜。其控制量不少于1個，而且所有控制量相互影響。一個變量的變化會引起與其相關的所有變量的變化，這不僅影響系統控制性能，而且影響生產過程的正常運行。為了解決由耦合現象所帶來的弊端，需要利用神經網絡將耦合的控制系統進行解耦。

為了獲得滿意的控制效果，研究人員根據多變量控制的理論和實踐，提出了多變量解耦控制。解耦的方法為:把多變量耦合系統變成多個獨立的單輸入單輸出控制系統，并利用單變量控制的成熟技術實現多變量系統的設計和控制。

單一的單神經元PID控制器可較好地實現單變量控制。多個單一的單神經元PID控制器構成的網絡就可以實現單神經元、多變量PID控制。單神經元PID多變量控制器與單神經元控制器的控制原理是一樣的，不同是:單神經元多變量PID控制器是多個輸入對應多個輸出;單神經元PID控制器是一個輸入對應一個輸出。本文的單神經元自適應多變量解耦PID控制器選擇單神經元自適應兩變量解耦PID控制器，其結構如圖1所示。

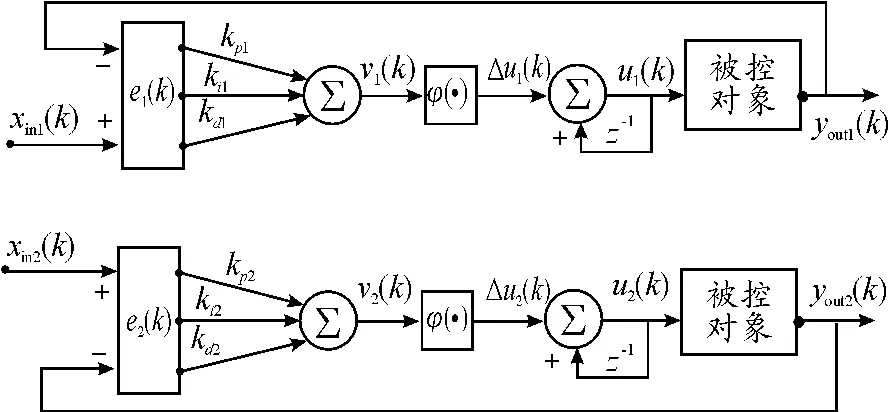
圖1 單神經元自適應兩變量解耦PID控制網絡結構

單神經元兩變量解耦PID控制器的工作原理和單神經元PID控制器的工作原理完全相同，只是輸入變為2個:xin1(k)和xin2(k)，輸出變量變為2個:yout1(k)和yout2(k)。

2 基于憶阻的單神經元自適應兩變量解耦PID控制器

根據單神經元兩變量解耦PID控制器的結構和憶阻器可以替代神經突觸的特性，用憶阻器替代單神經元兩變量PID控制網絡中的突觸權值，得到基于憶阻的單神經元兩變量解耦PID控制網絡結構，如圖2所示。

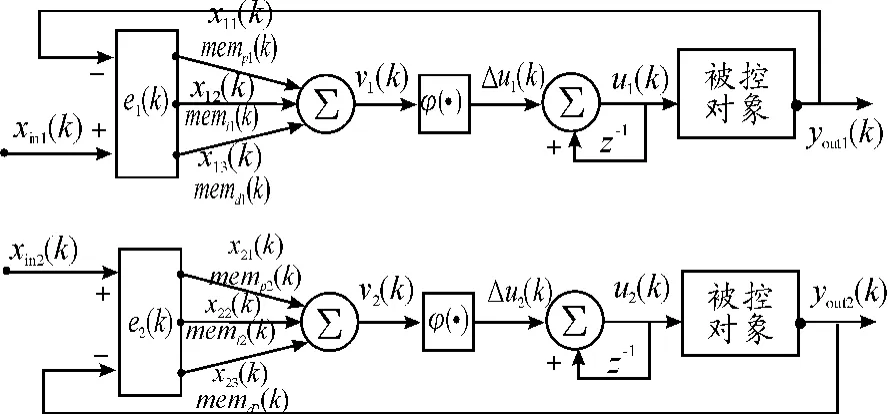
圖2 基于憶阻的單神經元自適應兩變量解耦PID控制網絡結構

基于憶阻的單神經元自適應兩變量解耦PID控制網絡的真正輸入是誤差信號e1(k)和e2(k)，表達式分別為:e1(k)=xin1(k)－yout1(k);e2(k)=xin2(k)－yout2(k)。2個誤差信號同時輸入到網絡中，PID控制網絡進行并行處理，2個單神經元PID控制器分別根據某學習規則，使突觸權值不斷進行學習修正，直到2個PID控制器的誤差都為零為止。

本文用憶阻器替代PID網絡中的比例、積分和微分系數，得到基于憶阻的PID兩變量控制器的突觸權值表達式:

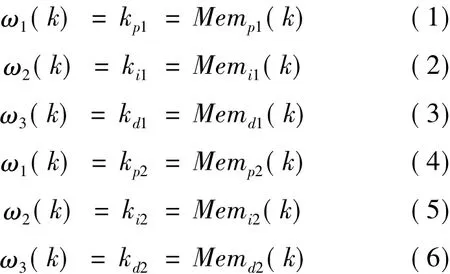
基于憶阻的PID兩變量控制器的輸入狀態量分別為:

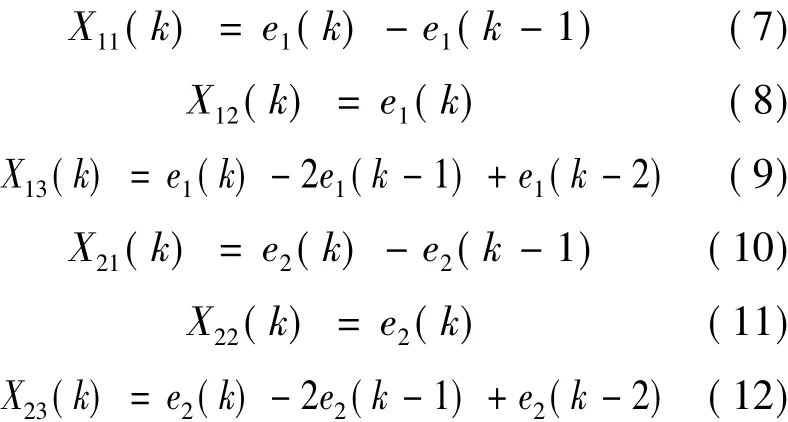
輸出作用律表達式分別為:

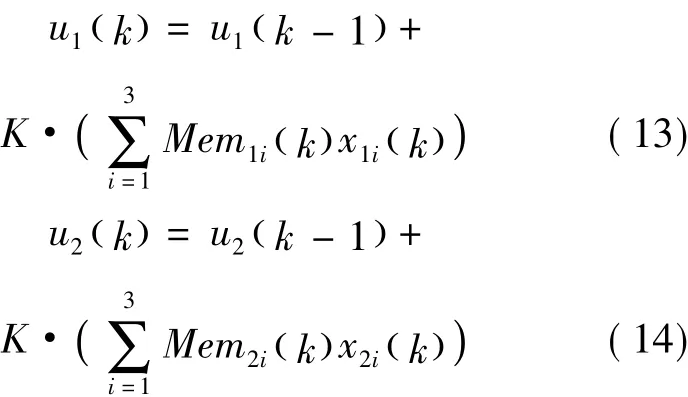
其中φ(·)是基于憶阻的單神經元自適應兩變量解耦PID控制網絡的激活函數，這里為神經元比例系數K，且為正實數，取值范圍為K∈(0，1)。

3 憶阻感知器不同學習規則下的基于憶阻的單神經元自適應兩變量解耦PID控制器的Matlab仿真

本文給定的輸入為單位階躍輸入，即xin1(k)=1，xin2(k)=0。PID控制器中2個變量的被控對象分別為:

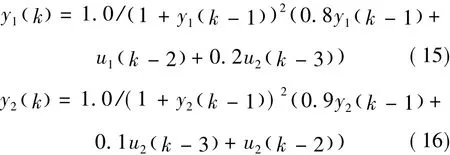
輸入信號的初始值分別為:x11=0，x12=0，x13=0，x21=0，x22=0，x23=0;2個PID網絡的學習效率為:αp=0，αi=0，αd=0;2個 PID 網絡的突觸權值的初始值分別為:Memp1=0.1，Memi1=1.1，Memd1=1.6;Memp2=0.01，Memi2=0.006，Memd2=0.005，采樣時間為 0.001s。

根據權值修正公式，得到不同規則下的位置跟蹤曲線(見圖3～6，其中虛線為輸入階躍信號xin1=1和xin2=0，光滑實線是輸出曲線yout1，實線是輸出曲線yout2)。

在無監督的Hebb學習規則下，基于憶阻的單神經元兩變量解耦PID控制器的突觸權重的修正公式為:在有監督的Hebb學習規則下，基于憶阻的單神經元兩變量解耦PID控制器的突觸權重的修正公式為:

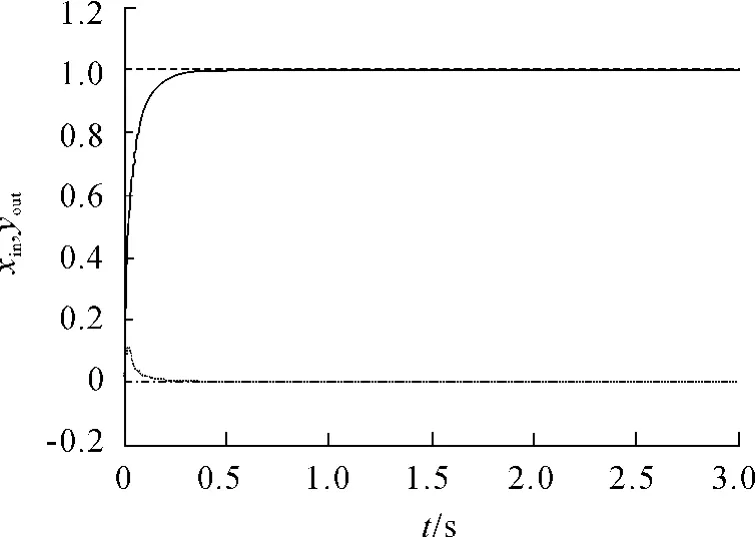
圖3 無監督的Hebb學習規則下的位置跟蹤曲線

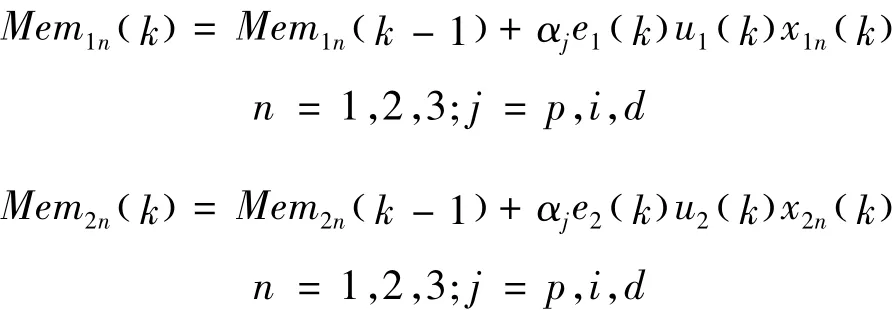
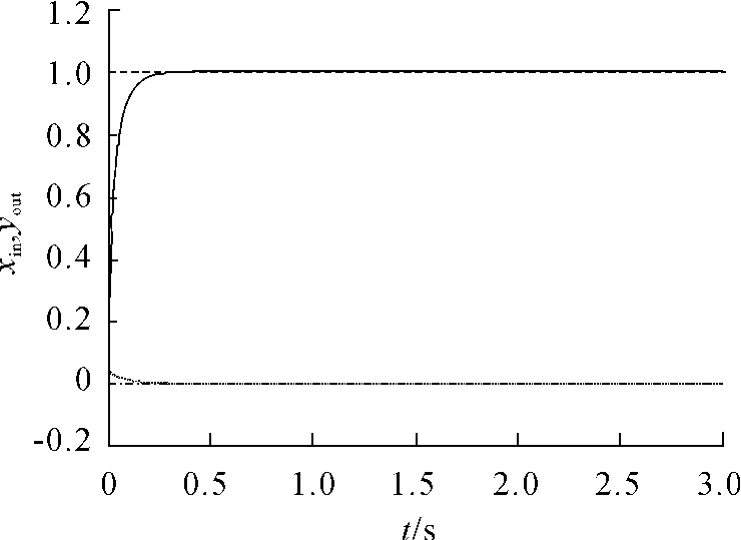
圖4 有監督的Hebb學習規則下的位置跟蹤曲線

在LMS學習規則下，基于憶阻的單神經元兩變量解耦PID控制器突觸權重的修正公式為:

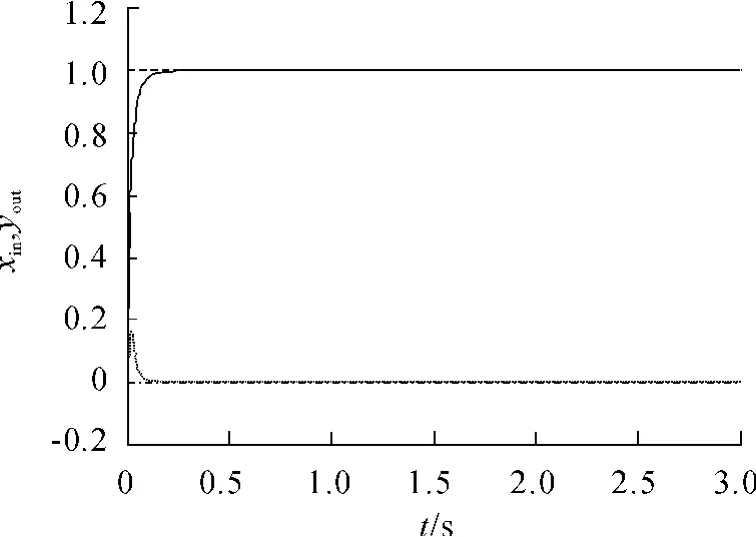
圖5 LMS學習規則的位置跟蹤曲線

改進的基于憶阻的單神經元兩變量解耦PID控制器的突觸權重的修正公式為:

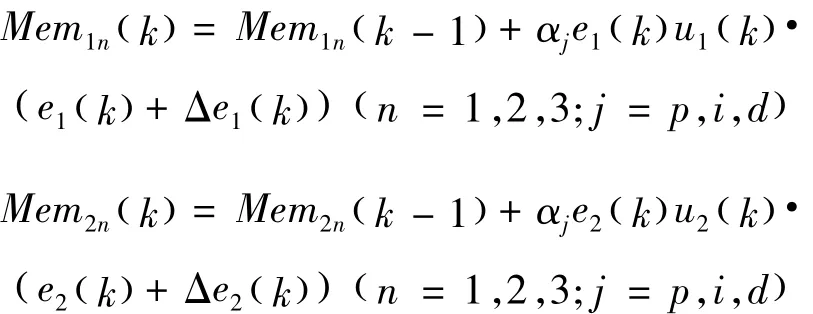
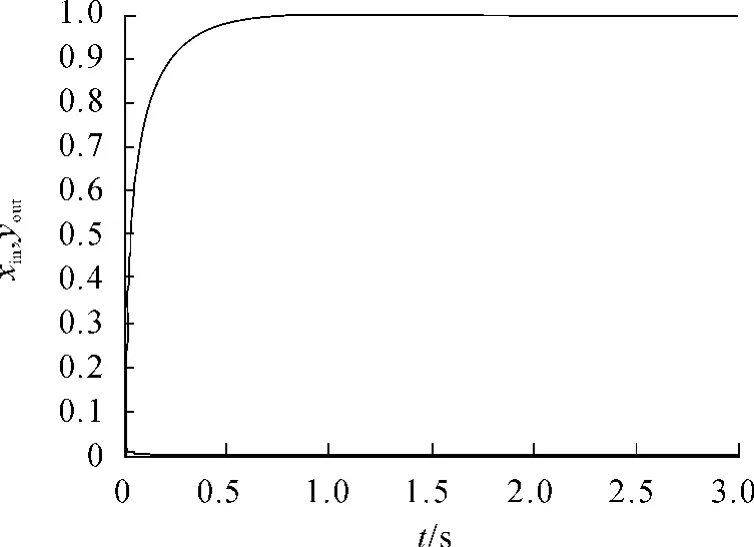
圖6 改進的學習規則的位置跟蹤曲線

4 基于憶阻的單神經元兩變量解耦PID控制器與單神經元兩變量解耦PID控制器的比較

在相同的初始值、相同的學習規則下，將基于憶阻的單神經元兩變量解耦PID控制器與單神經元兩變量解耦PID控制器的輸入輸出跟蹤曲線和誤差曲線分別進行分析比較，其曲線見圖7、8(兩控制器輸入分別為1和0，都為藍色線;黑色、紅色曲線分別是在控制器輸入為1時基于憶阻PID控制器和PID控制器的輸出曲線;品紅色、綠色曲線分別是在控制器輸入為1時基于憶阻PID控制器和PID控制器的輸出曲線)。

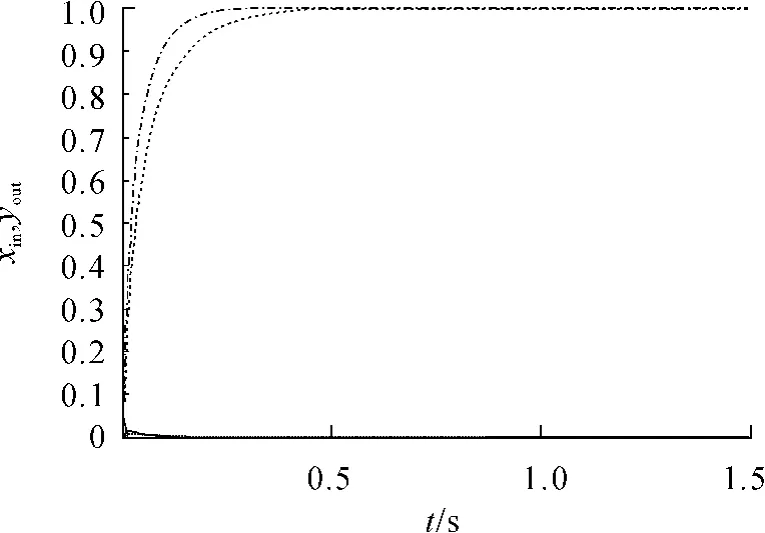
圖7 2個PID控制器的輸入輸出跟蹤曲線

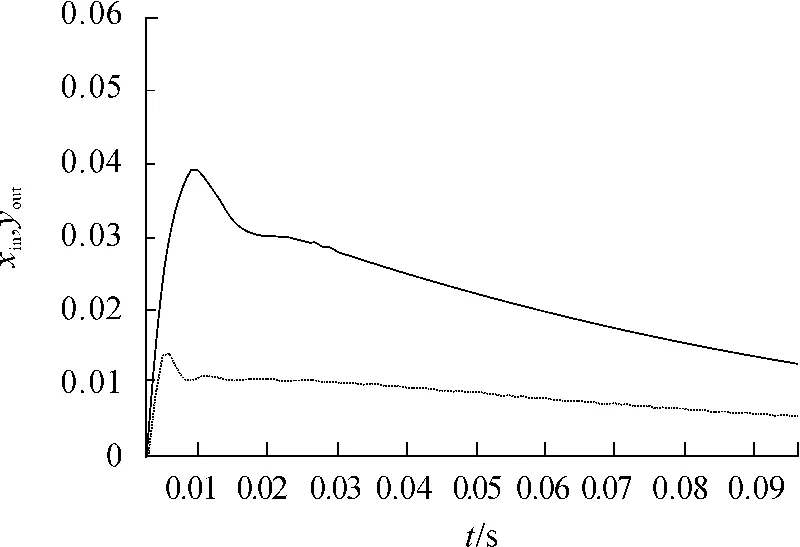
圖8 放大后的PID控制器的輸入輸出跟蹤曲線，輸入信號為xin(k)=0

從以上2個PID控制器的輸入、輸出曲線(圖7、圖8)，可以觀察到基于憶阻PID控制器(綠色)與PID控制器的輸出跟蹤曲線(品紅)相比，前者上升時間(輸入信號為xin(k)=1的情況下)和下降時間變短(輸入信號為xin(k)=0的情況下)，超調量變小，使整個系統的學習速度快，曲線擬合效果好，系統穩定，達到較好的自適應控制效果。

5 基于憶阻的單神經元兩變量解耦PID控制器的應用

倒立擺系統是一個典型的非線性、強耦合、多變量和不穩定系統。本文以一階倒立擺作為PID控制系統的被控對象，系統的2個輸入信號分別為階躍信號xin(k)=1和xin(k)=0，被控對象分別為倒立擺擺桿角度和小車位置。因此，構成了兩輸入兩輸出的兩變量控制系統。

擺桿角度的傳遞函數為

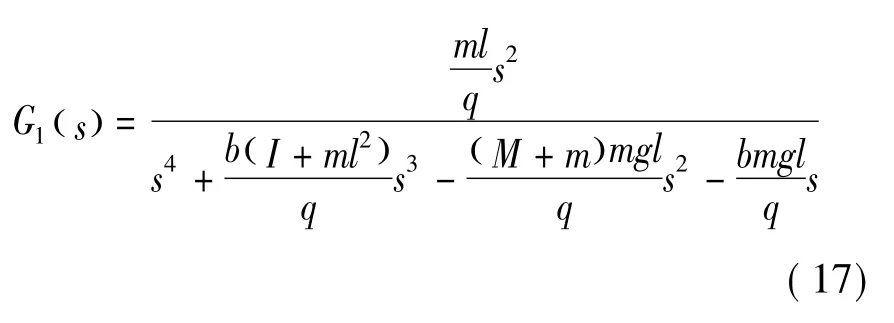
小車位置的傳遞函數為

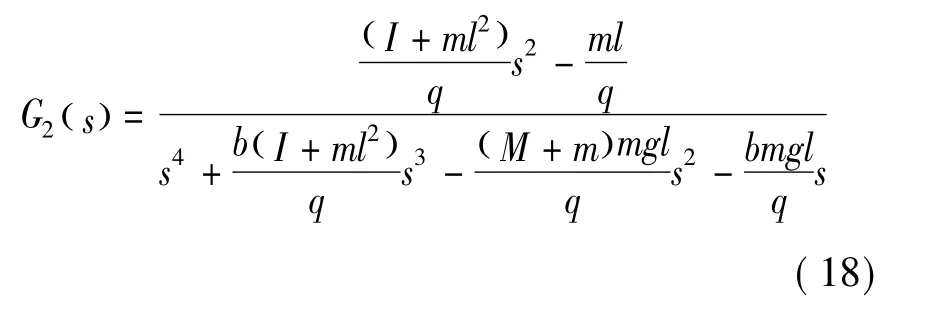
其中:M是小車質量;m是擺桿質量;b是小車摩擦因數;l為擺桿轉動軸心到桿質心的長度;I為擺桿慣量;ts為采樣時間。以上參數的取值分別是:b=0.1，M=0.5，m=0.2，g=9.8，I=0.006，ι=0.3，ts=0.001，q=(M+m)·(I+mι2)－ (mι)2。

從圖9可觀察到，系統的2個響應曲線跟蹤效果較好，而且擺桿角度跟蹤曲線超調比較小，整個系統的控制比較理想。

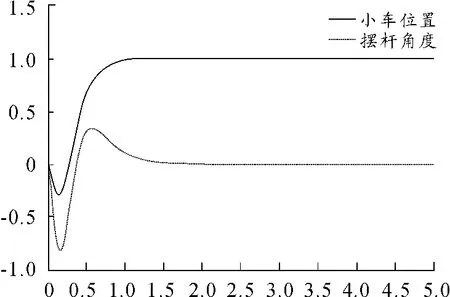
圖9 小車位置和擺桿角度跟蹤曲線

6 結束語

本文從理論闡述和仿真實驗2個方面對基于憶阻的單神經元多變量解耦PID控制器進行了分析。此系統不僅可以實現較好的跟蹤控制，而且誤差和超調量都比較小，權值學習修正速度較快，符合控制要求。由于憶阻器是納米級器件，所以有可能實現體積小、功耗低、精度高、功能強的超大規模集成(VLSI)電路和微控制器。本控制系統經過解耦設計后，整個控制系統振蕩明顯降低，且具有自適應能力強、響應速度快、兩變量控制效果好和抗干擾能力強等特點。基于憶阻的單神經元多變量解耦PID控制器的實現為基于憶阻的多輸入多輸出的單神經元多變量解耦PID控制器的實現和應用奠定了基礎。

［1］Yin Y H.The Intelligent PID control of filature production line slack-loop system［C］//2011 The 6th International Forum on Strategic Technology.Harbin:［s.n.］，2011:378－381.

［2］Bennett Stuart.A history of control engineering，1930 －1955［M］.［S.l.］:The Institution of Engineering and Technology(IET)，1993.

［3］Chen J，Cheng N，Zhang J.Neural based PID control for networked processes［C］//Proceedings of the 2011 4th International Symposium on Advanced Control of Industrial Processes.Hangzhou:［s.n.］，2011:466 －471.

［4］Chen X X，Wang C G，Wu H Z.PID:Controllers Parameters Self-tuning algorithm based on frequency characteristic［C］//2010 International Conference on Measuring Technology and Mechatronics Automation.Changsha:［s.n.］，2010:891 －894.

［5］Zhang Y H，Zhao D.Research on PID Controller Based on the BP Neural Network［C］//2011 International Conference on Electronic＆Mechanical Engineering and Information Technology.Harbin:IEEE，2011:516 －519.

［6］Guangjun Yang，Bing Xiao，Xiaojuan Zhu.A Method of Neuron PID Control Based on Fuzzy Regulating Gain［J］.Automatic Control and Meter，2004，19:44 －46.

［7］Chua L O.Memristor－ The Missing Circuit Element［J］.IEEE Transactions on Circuit Theory，1971:507－519.

［8］Chua L O.Device Modeling via Nonlinear Circuit Elements［J］.IEEE Transactions on Circuits and Systems，1980，27:1014 －1044.

［9］Sharifi M J，Banadaki Y M.General Spice Models for Memristor and Application to Circuit Simulation of Memristor-Based Synapses and Memory Cells［J］.Journal of Circuits，Systems，and Computers(JCSC)，2010，19:407－424.

［10］Corinto F，Ascoli A，Gilli M.Memristive Based Oscillatory Associative and Dynamic Memories［C］//Cellular Nanoscale Networks and Their Applications(CNNA)，2010 12th International Workshop on，2010:1 －6.