烘絲機逆動力學過程模糊辨識

何 忠，雷 李，張 里

(1.重慶卷煙廠，重慶 400060;2.重慶理工大學電子信息與自動化學院，重慶 400054)

烘絲機是卷煙制絲工藝過程中最重要的工藝設備之一，其主要功能是對煙絲進行干燥，使其含水率符合一定的工藝要求，從而改善煙絲的彈性和填充能力，以提高煙絲的感官質量。烘后煙絲水分是直接影響卷煙內在質量的重要參數［1］。

烘絲機結構示意圖如圖1所示。烘絲機的工作原理是以飽和蒸汽為加熱介質，為烘絲機滾筒筒體和熱風提供熱源，煙草葉絲跟隨烘絲機筒體炒料板的翻炒進行熱交換，從而達到葉絲干燥脫水目的［2］。由于烘絲過程是一類典型的涉及多變量、強耦合、時變、大滯后等多種因素的熱工過程，難以建立精確的數學模型［3］，再由于煙草本身具有的特殊性質，從而使得烘絲過程的水分控制十分困難、復雜。

圖1 烘絲機結構示意圖

在卷煙生產過程中，由于卷煙牌號的不同可能要采用不同產地、不同品質的煙葉。在不同牌號卷煙的烘絲過程中，相關工藝參數需要進行試車、調整，一方面要耗費一定數量的煙絲原料，另一方面又要耗費較長的時間進行工藝參數的整定。

本文基于逆動力學辨識的思想，建立了基于某型滾筒式烘絲機的烘絲過程數學逆模型，為烘絲過程的工藝參數優化、提高煙絲水分控制精度奠定了基礎，同時也為卷煙烘絲過程節能降耗，增加經濟效益提供了一條可行的途徑。

1 逆動力學過程模糊辨識基礎

1.1 逆動力學模糊規則模型

根據系統的輸出過程來確定導致此輸出的輸入過程是逆動力學方法的核心思想所在［4］。以SISO系統為例，若系統輸入為u，輸出為y，則可以采用 T－S結構［5］構建該系統的逆動力學過程模型:

模糊規則

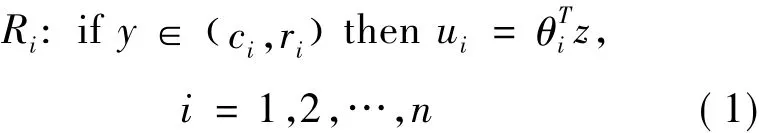
自適應模糊推理

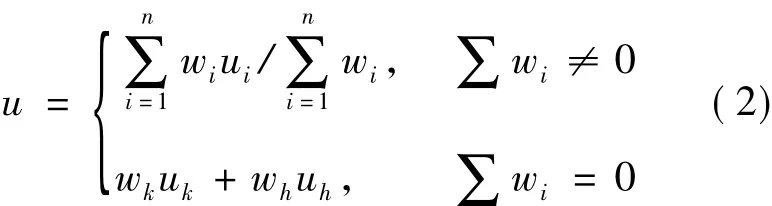
其中:z= 1，y[ ]TT為廣義輸入向量;n為模糊規則數量，仿真經驗表明其取值一般不大于3。如果模糊規則的輸入向量y(即系統的輸出)落在球心為ci、半徑為ri的廣義球體內，則啟采用第i條規則來求取系統的輸入(即模糊規則的輸出)中心ui。各權系數wi根據輸入向量y與各局部區域中心ci之間的歐氏距離來計算［6］:

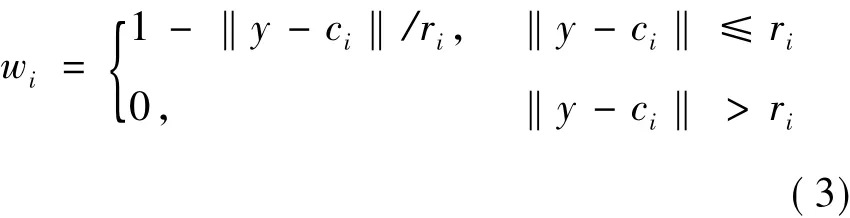
特別地，如果新輸入數據沒有落在訓練樣本輸入區域的范圍內，則通過與之距離最近的2個局部輸入區域的模糊規則來進行計算，其權值wk和wh按下式計算:

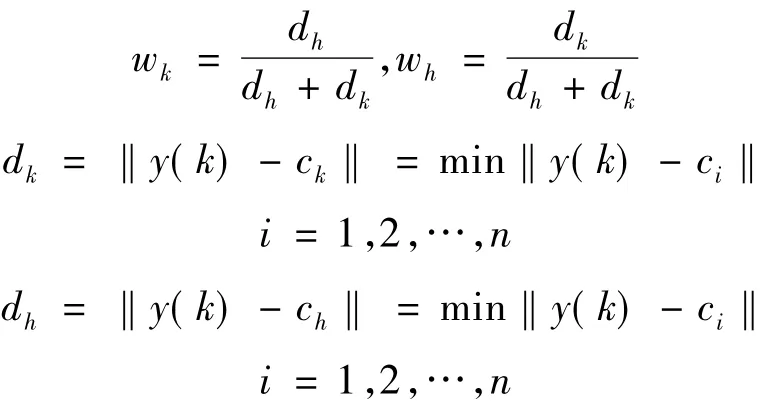
且 i≠k。

逆動力學模糊規則模型的輸入向量y應該結合具體應用背景來構造。一般分為2種情況:當通過已知的系統輸出過程反求此輸出的輸入過程時，可以視為一種離線分析或診斷過程，其輸入向量y采用下列結構即可:

而當需要進行在線實時控制時，即要求依據系統的期望輸出過程來反演系統的輸入過程時，輸入向量y一般可按下述結構設計:

其中:u－ = [u(k－1)，u(k－2)，…，u(k－mu)]表示系統輸入歷史數據向量;y－=［y(k－1)，y(k－2)，…，y(k－my1)］表示系統輸出的當前數據和歷史數據向量;y+=［y(k+1)，y(k+2)，…，y(k+my2)］表示所期望的系統輸出數據向量。

1.2 模糊規則的結構、參數辨識

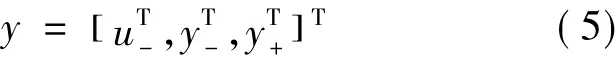
逆動力學模糊規則模型的建立需對模型的前后件的結構和參數進行辨識，即辨識各局部輸入區域(ci，ri)及動態參數向量θi。在此引入熵的概念對輸入空間進行初始聚類。對于維數為n的輸入向量 y，按式(6)、式(7)［7］確定各樣本的熵 Ej以及數據 yi和 yj之間的近似度 Si，j。

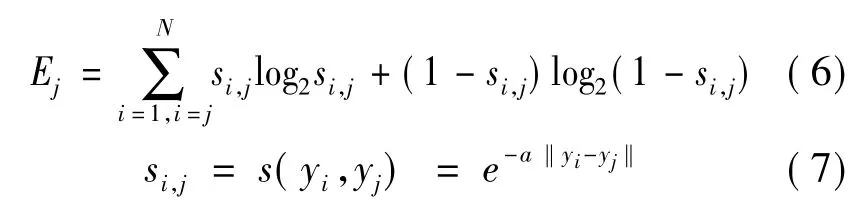
式中:σ為數據樣本之間的平均距離;α=－ln(0.5/σ)。首先人工確定決策常數 β∈［0，1］，再以對應minEj的輸入數據點yc1作為局部數據區域的初始中心c1，然后從輸入向量y中剔除掉滿足條件S(yj，c1)＞β的樣本，再在剩余的樣本集中確定區域的中心c2。依此類推，直至y為空集，可以確定初始局部輸入區域的中心為C=(c1，c2，…，cn)。設定各區域的初始半徑為r=0，i=1，…，n，采用競爭學習算法修正各區域中心及半徑［8］。在獲得的各局部輸入區域(ci，ri)的基礎上，任選擇一組訓練樣本y(k)，u(k)，采用遞推最小二乘法刷新各模糊規則的動態參數θi:

若‖y(k)－ ci‖≤ri，則:

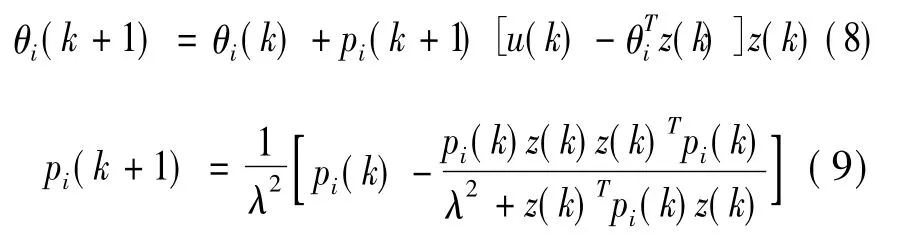
若‖y(k)－ ci‖ ＞ ri，則［9］:

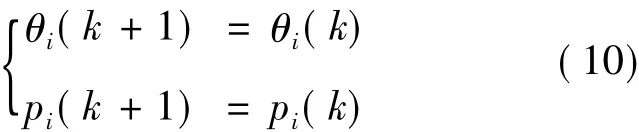
式中 λ 為遺忘因子，一般取值為［0.90，0.99］。遞推初始時，取 θi=0，pi=αI，其中 I為單位矩陣;取α=105。

3 烘絲過程的逆模型辨識

煙絲烘絲過程是一個多輸入多輸出的MIMO系統，各種控制參數之間的耦合關系十分復雜，但經驗表明，熱風溫度是對煙絲水分影響權值最高的控制參數，也是在實際生產中最主要的控制參數，故本文以某型烘絲機的現場生產數據為基礎，基于逆動力學模糊規則建立熱風溫度與煙絲出口水分之間的關系模型。圖2、3分別為某型烘絲機熱風溫度和煙絲出口水分的現場采樣數據，采樣周期均為5 s。

本文選擇熱風溫度u(t－1)，u(t－2)以及煙絲出口水分y(t+4)，y(t+5)作為逆模糊規則模型的輸入變量，模型輸出為t時刻的熱風溫度u(t)。取前200組數據，經離線辨識得對象逆動力學過程初始模糊規則模型(局部輸入區域數選擇為2):

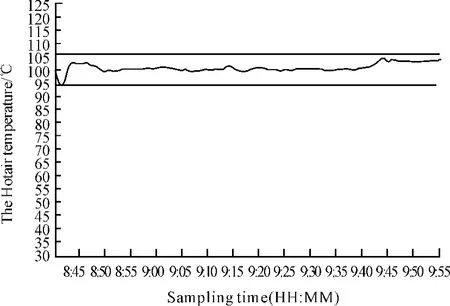
圖2 熱風溫度變化曲線

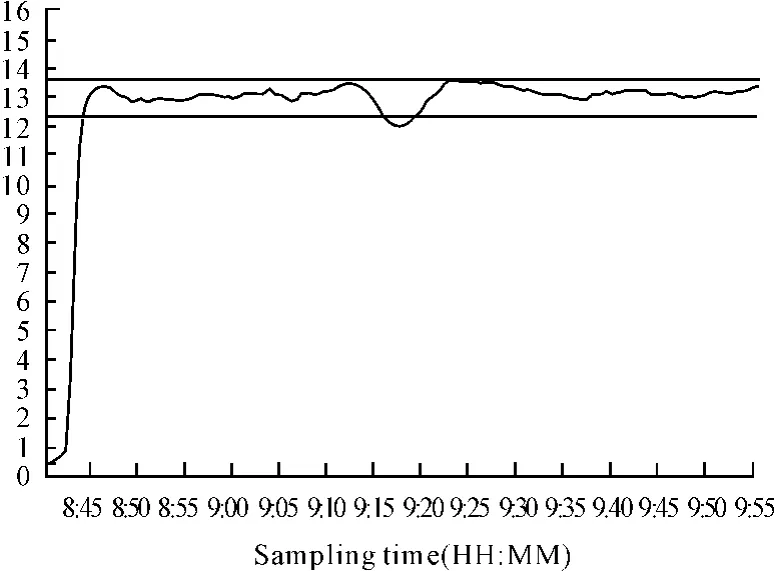
圖3 烘絲機出口煙絲水分變化曲線

采用后200組數據進行在線辨識驗證，即以后200點烘絲機出口水分采樣值作為系統輸入，在初始模糊規則模型的基礎上，在線刷新模糊規則的動態參數θi，得到逆動力學模型的輸出，記為um(k)，其與實際對應的熱風溫度值之差為▽u(k)=u(k)－um(k)，其結果如圖4所示。

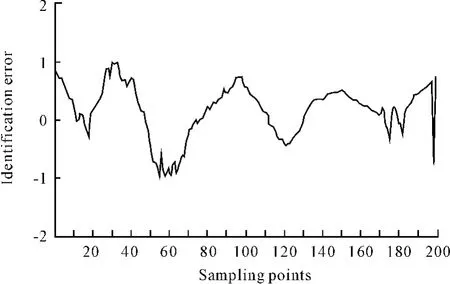
圖4 烘絲機逆動力模型辨識結果誤差變化曲線

4 結束語

本文基于逆動力學模糊辨識理論，以生產現場的實際采樣數據為基礎，建立了烘絲機出口煙絲水分與烘絲機熱風溫度的逆動力學模型。仿真結果表明:辨識結果具有較高的精度，誤差峰值小于1%。而如何將逆動力學辨識應用于MIMO系統，實現多參數的系統辨識將是值得繼續探討的課題。

利用系統的輸出要求反演系統的控制輸入是逆動力學辨識應用于控制的思想內核。烘絲機工藝參數的優化及控制效率的提高具有巨大的經濟和社會效益。將逆動力學辨識的思想應用于烘絲機控制無疑為煙草行業工藝過程的優化開辟了一條值得期待的途徑。

［1］王艷紅，韓光勝.煙草烘絲過程的水分控制［J］.北京工業大學學報:自然科學版，2000，26(4):90－95.

［2］饒琳，陳良元，席年生.分段式低溫滾筒葉絲干燥設備研究［J］.新技術新工藝，2009(10):95－97.

［3］王廣軍，何祖威，陳紅.基于神經網絡和過程機理特性的鍋爐蒸發系統仿真［J］.中國電機工程學報，2001，21(11):65－68.

［4］鄧良才，王廣軍，陳紅.鍋爐汽溫對象的在線模糊辨識［J］.中國電機工程學報，2006，26(9):111 －115.

［5］Takagi T，Sugeno M.Fuzzy identification of systems and its applications to mod eling and control［J］.IEEE Trans Syst，1985，15(1):116 －130.

［6］岳玉芳，毛劍琴.一種基于T－S模型的快速自適應建模方法［J］.控制與決策，2002，17(2):155 －158.

［7］黃艷新，周春光，楊國慧，等.基于熵聚類模糊神經網絡味覺信號識別系統的研究［J］.計算機研究與發展，2004，4l(3):414 －419.

［8］呂劍虹，陳建勤，劉志遠，等.基于模糊規則的熱工過程非線性模型的研究［J］.中國電機工程學報，2002，22(11):132－137.

［9］王廣軍，朱麗娜，沈曙光.一種基于逆動力學模糊規則的自適應控制方法［J］.系統仿真學報，2008，20(15):3907－3910.