基于奇異值差分譜與改進包絡分析的軸承故障特征提取
楊望燦,張培林,王懷光,陳彥龍
(軍械工程學院 七系,石家莊 050003)
滾動軸承是旋轉機械中應用廣泛但也易損壞的零件,據不完全統計,旋轉機械的故障約有30%是因滾動軸承發生故障引起的[1]。因此,對軸承的狀態進行監測和故障診斷顯得極為重要,如何有效地從混有強烈噪聲的原始振動信號中提取到軸承故障特征是軸承故障診斷的關鍵。
奇異值分解(Singular Value Decomposition,SVD)能夠將信號分解為一系列線性分量的疊加,具有零相移、波形失真小等優點[2],在信號處理和圖像去噪等方面得到了廣泛的應用[3-6]。奇異值分解在進行故障信號分析時關鍵在于如何合理地選擇有效奇異值來重構信號,并提取故障特征[7]。奇異值分解的特點決定了原始信號經奇異值分解重構后,重構信號中仍不可避免地存在殘余噪聲信號,造成對重構信號包絡解調分析時仍存在干擾頻率,影響軸承的故障特征提取和故障診斷。
針對此問題,提出了一種基于奇異值差分譜和改進包絡分析的軸承故障特征提取方法。首先采用奇異值分解方法對信號進行分解,然后根據奇異值差分譜圖中最大峰值的位置確定含有軸承故障特征的分量所對應的奇異值來重構信號,最后利用改進包絡分析在頻域里將重構信號中的殘余噪聲消除,凸顯軸承故障頻率,完成軸承的故障特征提取,診斷軸承故障。
1 奇異值差分譜理論
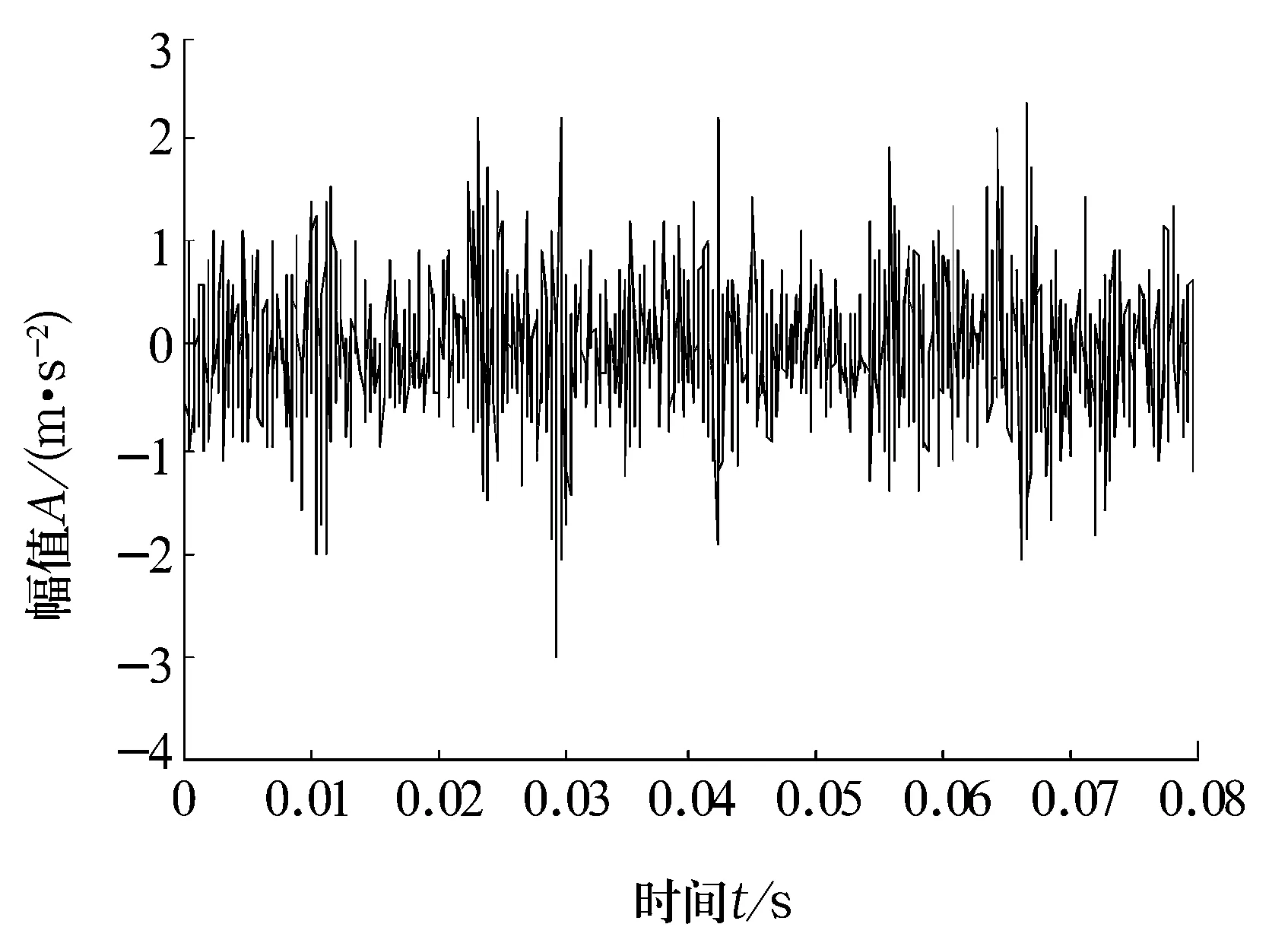
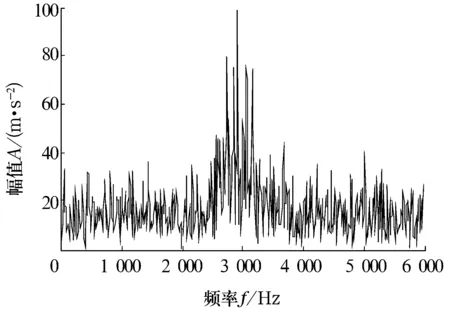
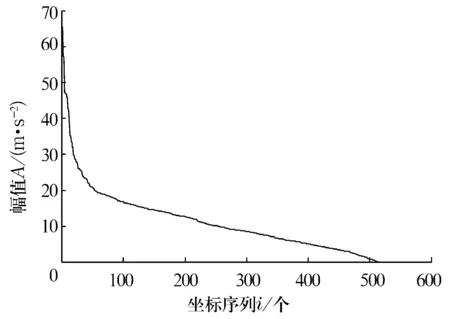
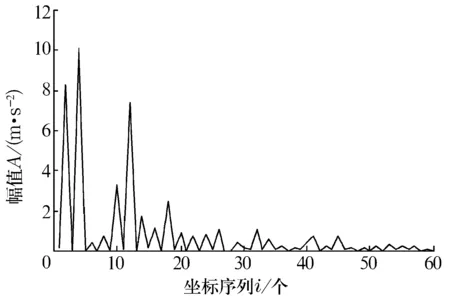
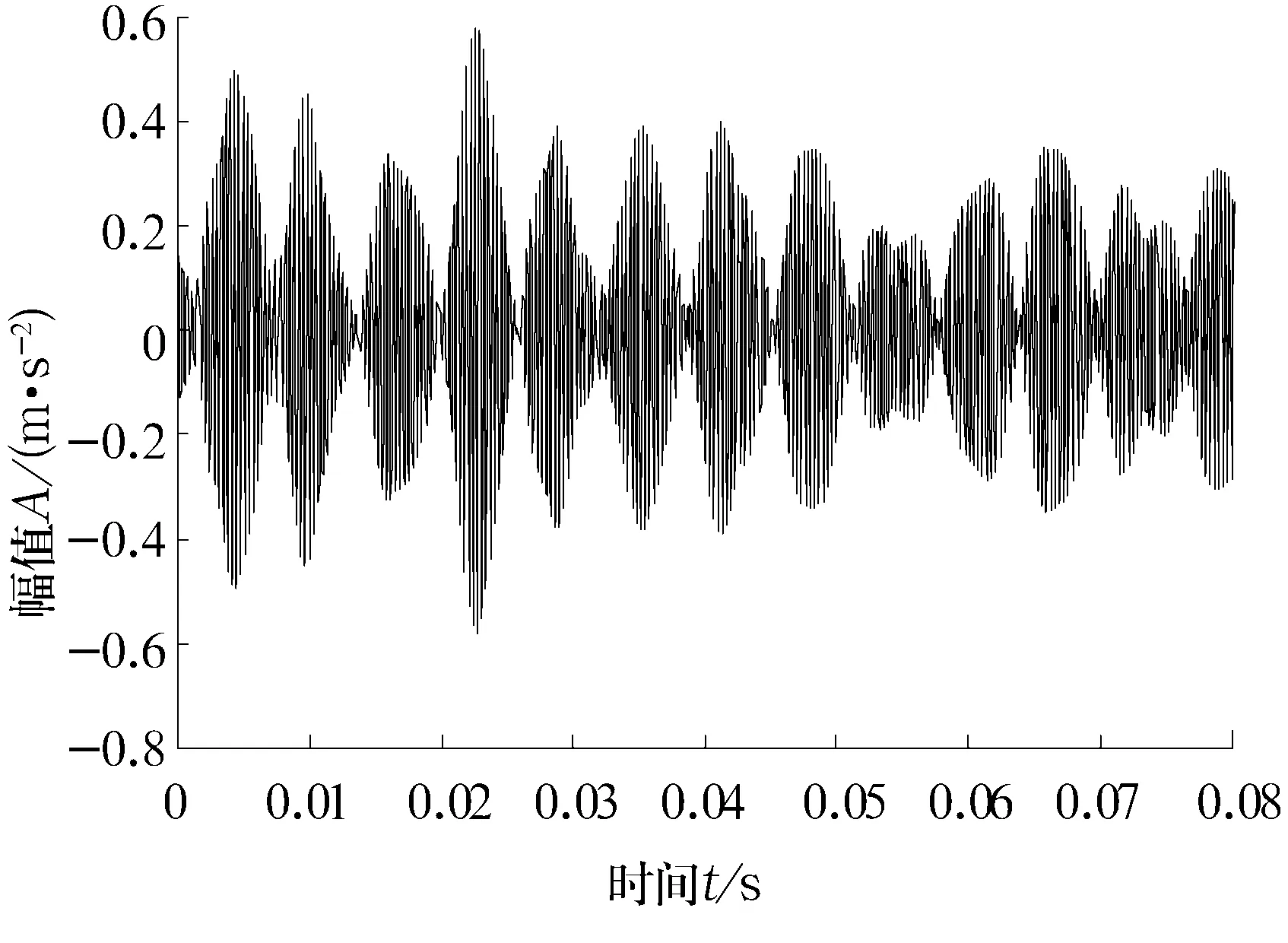
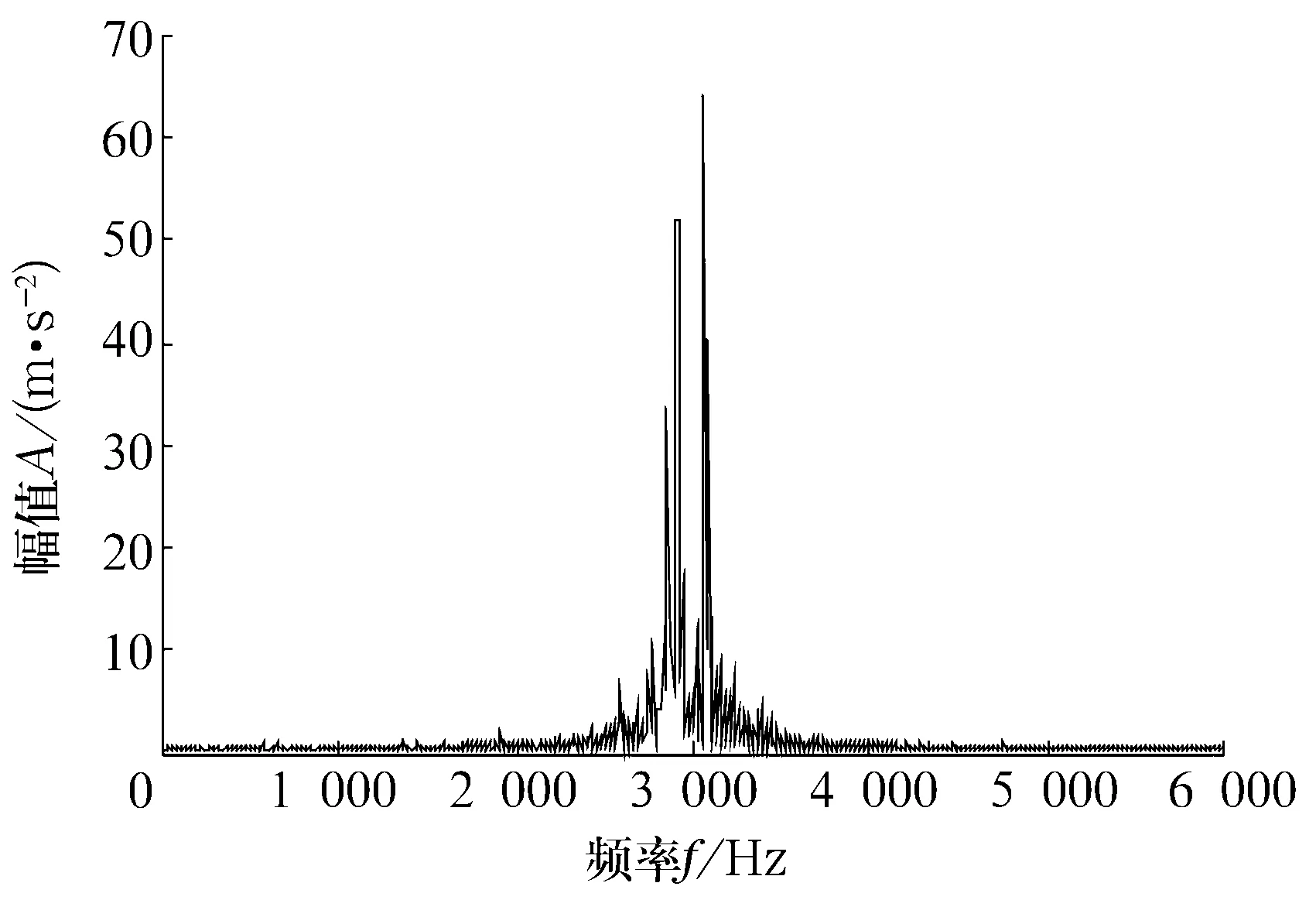
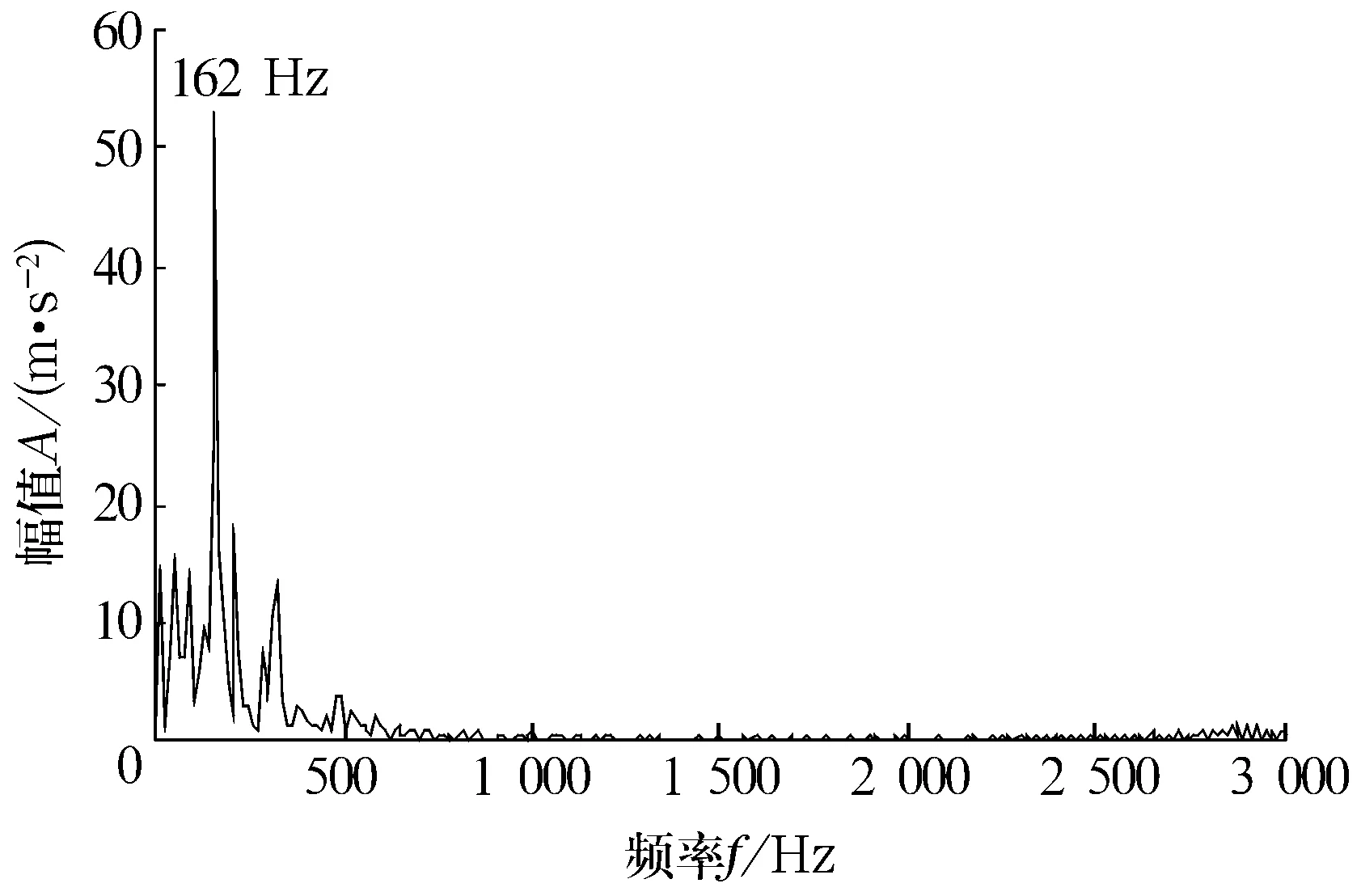
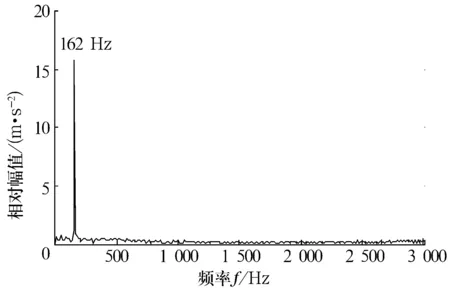
若A是m×n的矩陣(假設m>n),A的秩為r(r A=UDVT, (1) (2) 由(2)式可得,矩陣A也可以說是以非零奇異值為權重,相對應的左、右奇異向量做外積后的加權和,可見奇異值的選取是矩陣A重構的關鍵。 假設采集到的離散信號X=[x(1),x(2),…,x(N)] ,x(i)=s(i)+u(i),s(i)為有用信號,u(i)為噪聲信號,利用信號X可以構造Hankel矩陣 A= (3) 其中,1 (4) Ai= (5) 由Hankel矩陣結構特點可得,將其第1行和最后一列的數據首尾相接,可以得到長度為N的離散分量信號Pi,這樣,按照此種分解方法就構成了對原始信號的分解,即 (6) 所以,SVD的實質是將原始信號分解為一系列分量的線性疊加,這種線性疊加可以方便地選取合適分量重構信號,而且不會產生相位偏移,所以問題的關鍵是如何選取合適的有用分量。 觀察Hankel矩陣,下一行的數據比上一行滯后一個數據點。對于無噪聲信號,由于相鄰兩行具有相關性,這種信號構造的Hankel矩陣是一種病態矩陣,前面k個奇異值較大,后面的接近于零,奇異值有明顯的突變,而對于噪聲信號,相鄰兩行數據沒有相關性,其構造的Hankel矩陣的奇異值沒有明顯的突變,所以用奇異值差分譜[8]描述含噪信號的奇異值突變,從而選取有效的奇異值重構信號。 設C為奇異值由大到小形成的序列,C=[σ1,σ2,…,σr]。定義 bi=σi-σi+1(i=1,2,…,r-1), (7) 則所有的bi構成序列B=[b1,b2,…,br-1],序列B即為奇異值的差分譜。差分譜圖反應了相鄰奇異值之間的變化情況,最大峰值處代表了奇異值序列的最大突變,由于有用信號和噪聲的相關性不同而導致2種信號在奇異值上表現出最大的差異,這個最大突變點也反映了有用信號和噪聲信號的分界,所以,利用奇異值差分譜能夠自動地確定有用分量的個數。 同時注意到在構造上述Hankel矩陣時,有用信號和噪聲信號同時包含其中。由于噪聲信號的Hankel矩陣為良態滿秩矩陣,經過上述奇異值分解后,噪聲信號分布在每個奇異值對應的分量中,提取到的有用分量中仍然不可避免地存在著噪聲信號,這也是由奇異值分解的特點決定的,因此需要對重構后的信號進一步做去噪處理,提取信號特征。 在工程實際中,滾動軸承的故障振動信號多為受到背景噪聲和其他振動頻率干擾的幅度調制信號,需要采用包絡解調分析提取故障特征。SVD得到的重構信號中仍含有殘余噪聲,而包絡解調分析方法本身不具有去噪的功能,而且易受噪聲干擾,所以采用改進包絡分析,在頻域中進一步去除殘余噪聲,減小干擾頻率的影響,這樣對處理后的信號再進行包絡解調,可以使得軸承的故障頻率突出。 對重構信號進行頻域變換后殘余噪聲在幅值譜上會表現為幅值較小的干擾頻率,通過對Shannon熵的定義的修改[9-10],利用改進Shannon熵函數消除這些干擾頻率,再變換到時域后,殘余噪聲即可被消除。 定義改進的Shannon熵函數為 (8) (9) (m-1)]1/2。 (10) 上述處理完成后,重構信號的幅值譜中幅值高的主要頻率成分突出,幅值低的干擾頻率被去除。這樣,頻域去噪后的信號變換成時域信號再進行包絡解調,包絡譜中就能夠突出軸承故障頻率,避免殘余噪聲信號的影響,清晰有效地提取軸承的故障特征。 在一個齒輪箱上采集得到實際的滾動軸承信號,軸承型號為SKF 6205,在測試軸承內圈上利用電蝕加工單點故障,加速度傳感器安裝在驅動端的軸承座上。采樣數據是在電動機轉速為1 797 r/min下采集到的,采樣頻率為12 kHz,采樣點數為1 024。根據內圈故障計算公式可得內圈單點故障頻率為162.2 Hz。實測內圈故障信號的時域波形和頻譜圖如圖1和圖2所示。 對于軸承而言,當其滾道有損傷時,其時域信號會出現周期性的沖擊信號,由于受到軸承共振調制的影響,其特征頻率主要集中在中、高頻率段。觀察圖1和圖2,無法辨別出軸承是否發生故障,圖2中雖然中頻段幅值較大,但整個頻帶都存在頻率成分,軸承故障信號受噪聲干擾嚴重,無法獲取軸承振動情況的準確信息。利用采集到的信號構造Hankel矩陣,進行奇異值分解。采集到的離散數據點為1 024個,為了充分利用數據,構造行數為513,列數為512的最大階數的Hankel矩陣,得到512個奇異值。奇異值序列和奇異值差分譜如圖3和圖4所示。 圖1 內圈故障的時域波形 圖2 內圈故障的頻譜圖 圖3 奇異值序列 圖4 奇異值差分譜 從圖3可以看出奇異值的變化趨勢,從圖4可以看出奇異值的突變主要發生在奇異值序列的前部,為了清楚顯示,將奇異值差分譜前60個數據局部放大,如圖5所示。 圖5 奇異值差分譜的前60個數據點 從圖5可以清晰地看到第4個坐標點的峰值最大,這樣根據奇異值差分譜理論可以自動地確定重構信號的有用分量的個數為4,完成對原始信號的重構,去除噪聲,提取故障軸承的調幅特征。重構信號的時域波形和Fourier頻譜圖如圖6和圖7所示。 圖6 重構信號的時域波形 圖7 重構信號的頻譜圖 從圖6可以看到故障軸承信號的調幅特征,由于內圈存在凹坑,使得軸承運轉過程中滾動體受到凹坑的撞擊產生周期性沖擊,產生了調幅特征。在圖7所示的頻譜圖中重構信號的頻率主要集中在3 kHz附近,對照圖2可以看到噪聲信號產生的其他頻率段的大部分干擾頻率被剔除,主要頻率成分比較突出。但是由于奇異值分解的特點,重構信號中仍保留了部分殘余噪聲。從圖7中可以看到變換到頻域后重構信號的主要頻率成分附近還存在一些低幅值的干擾頻率。殘余噪聲在對信號做Hilbert包絡解調時會產生較大影響,因此需要進一步去除。對奇異值分解后的重構信號直接做Hilbert包絡解調,結果如圖8所示。采用改進包絡分析方法進行頻域去噪,突出幅值高的主要成分,削減低幅值的干擾成分,去除殘余噪聲,然后變換為時域信號做Hilbert包絡解調,結果如圖9所示。 圖8 重構信號的包絡譜 圖9 重構信號的改進包絡譜 圖8中除了故障頻率外,仍然受到雜頻的干擾。從圖9中可以看到162 Hz的頻率非常突出,而且幾乎沒有干擾頻率,與內圈的理論故障頻率162.2 Hz非常接近,可以認為提取到的特征頻率是內圈的故障頻率。 研究了基于奇異值差分譜與改進包絡分析的軸承故障特征提取方法,奇異值差分譜理論克服了以經驗為主選取奇異值重構信號的弊端,利用奇異值差分譜的最大峰值自動選取奇異值重構原始信號,既去除了實測信號中的大量噪聲,又保留了與軸承故障有關的有用信息。針對奇異值分解方法中仍會存留部分殘余噪聲的問題,利用改進包絡分析的方法在頻域范圍內進一步去除殘余噪聲,提取到的軸承故障特征頻率清晰突出,消除了干擾頻率的影響,效果非常明顯。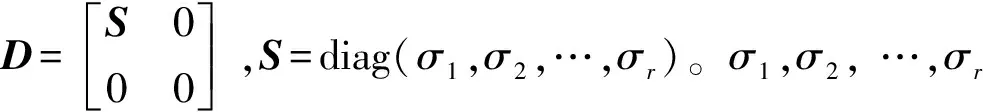
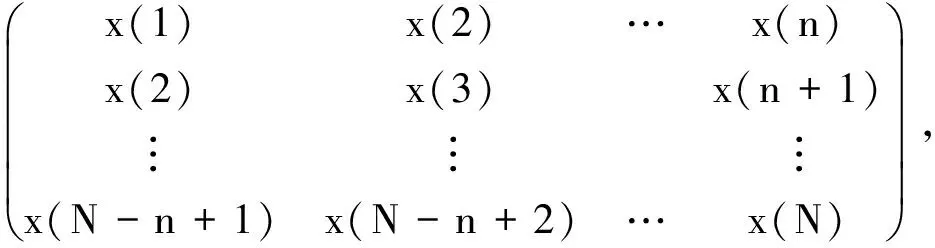
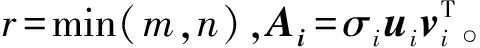
2 改進包絡分析
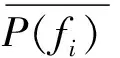
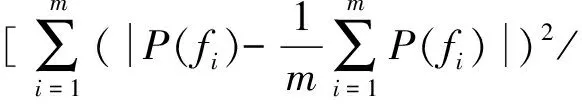
3 軸承故障信號分析

4 結束語

