基于等效磁荷法用蒙特卡洛法計算永磁軸承磁力
張鋼,張堅,張海龍,孟慶濤,樊曼
(上海大學 機電工程與自動化學院,上海 200072)
永磁懸浮軸承(以下簡稱永磁軸承)是利用永磁體在氣隙中產生的磁場實現轉軸穩定懸浮于空間的一種新型高技術軸承。由于其具有壽命長、無磨損、無需潤滑等顯著優點,因此得到了廣泛關注和研究[1-7]。承載能力和剛度計算是永磁軸承研究與設計過程中的重要環節。而永磁軸承的磁力解析計算,目前常用的方法是利用等效磁荷法或分子電流法建立磁力模型,通過求解一個復雜的四重積分得到[4-7]。由于四重積分求解比較復雜,有學者直接用Matlab中的符號積分函數求解,不僅計算周期長,而且往往得不到正確的數值解;也有學者用C++進行編程求解,但是編程過程較為復雜[7]。
基于以上原因,提出應用蒙特卡洛法對基于等效磁荷法建立的永磁軸承磁力模型的四重積分方程組進行求解;并與ANSYS分析得到的磁力值進行比對。
1 永磁軸承磁力模型
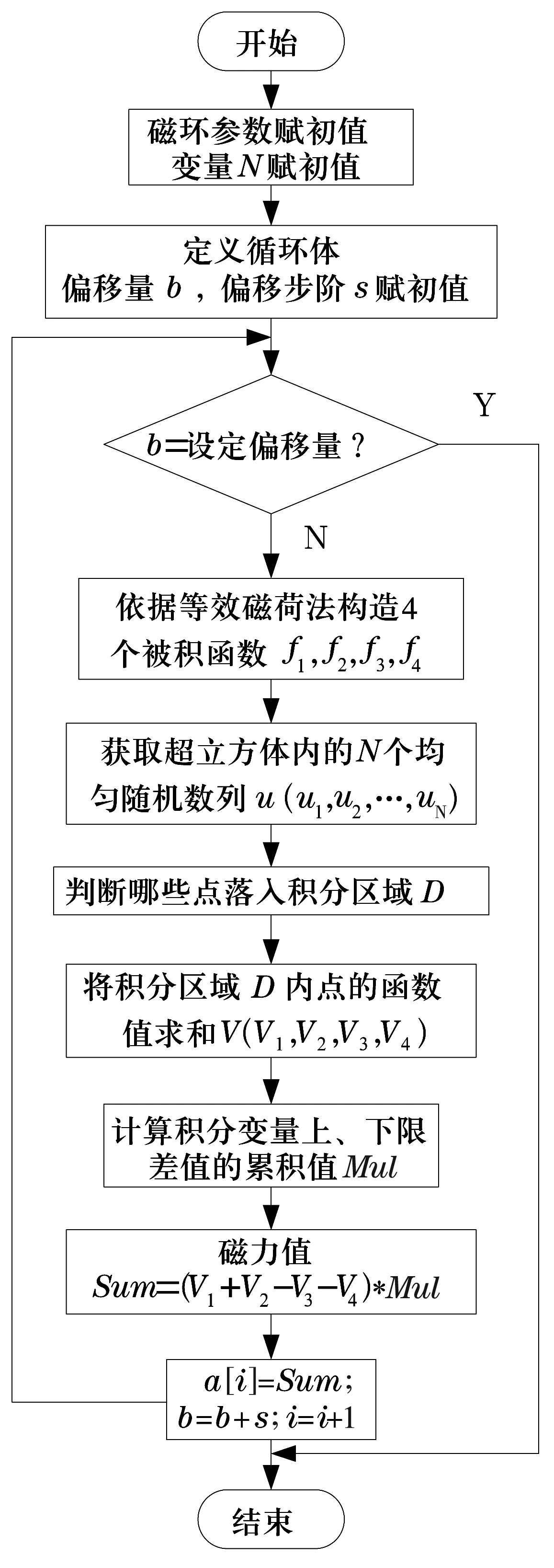
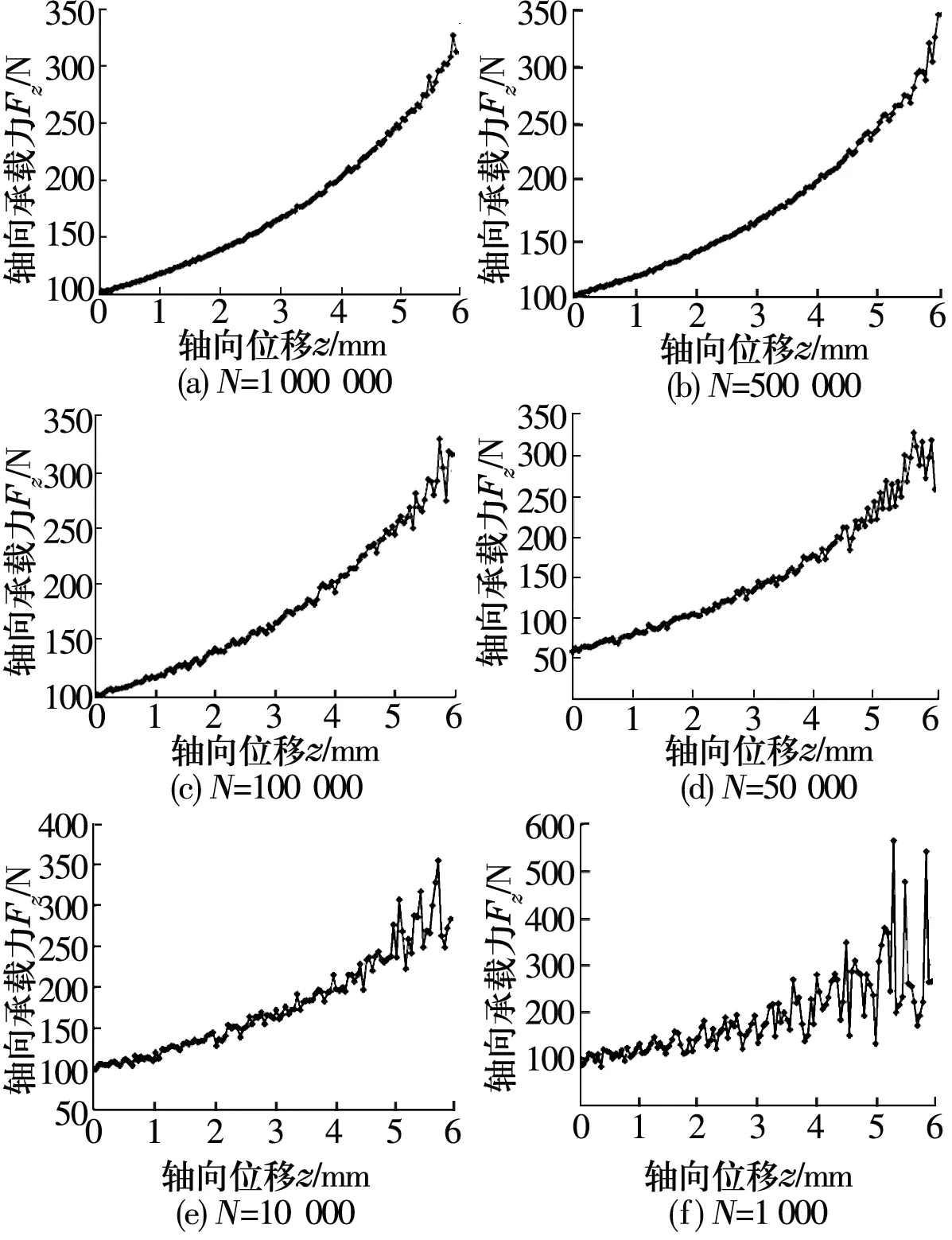
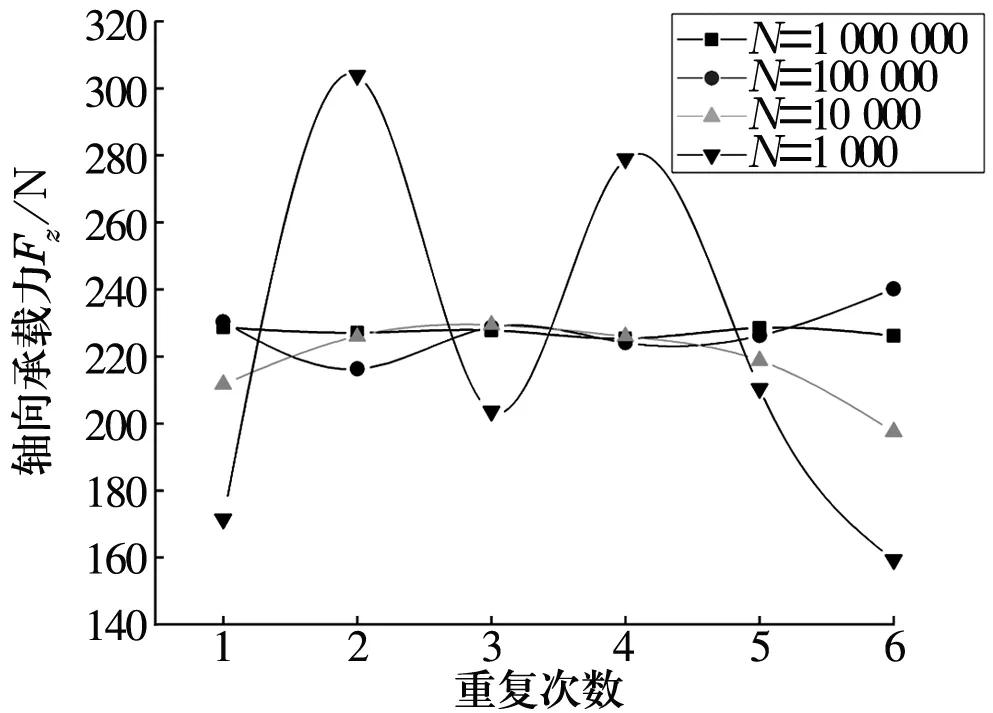
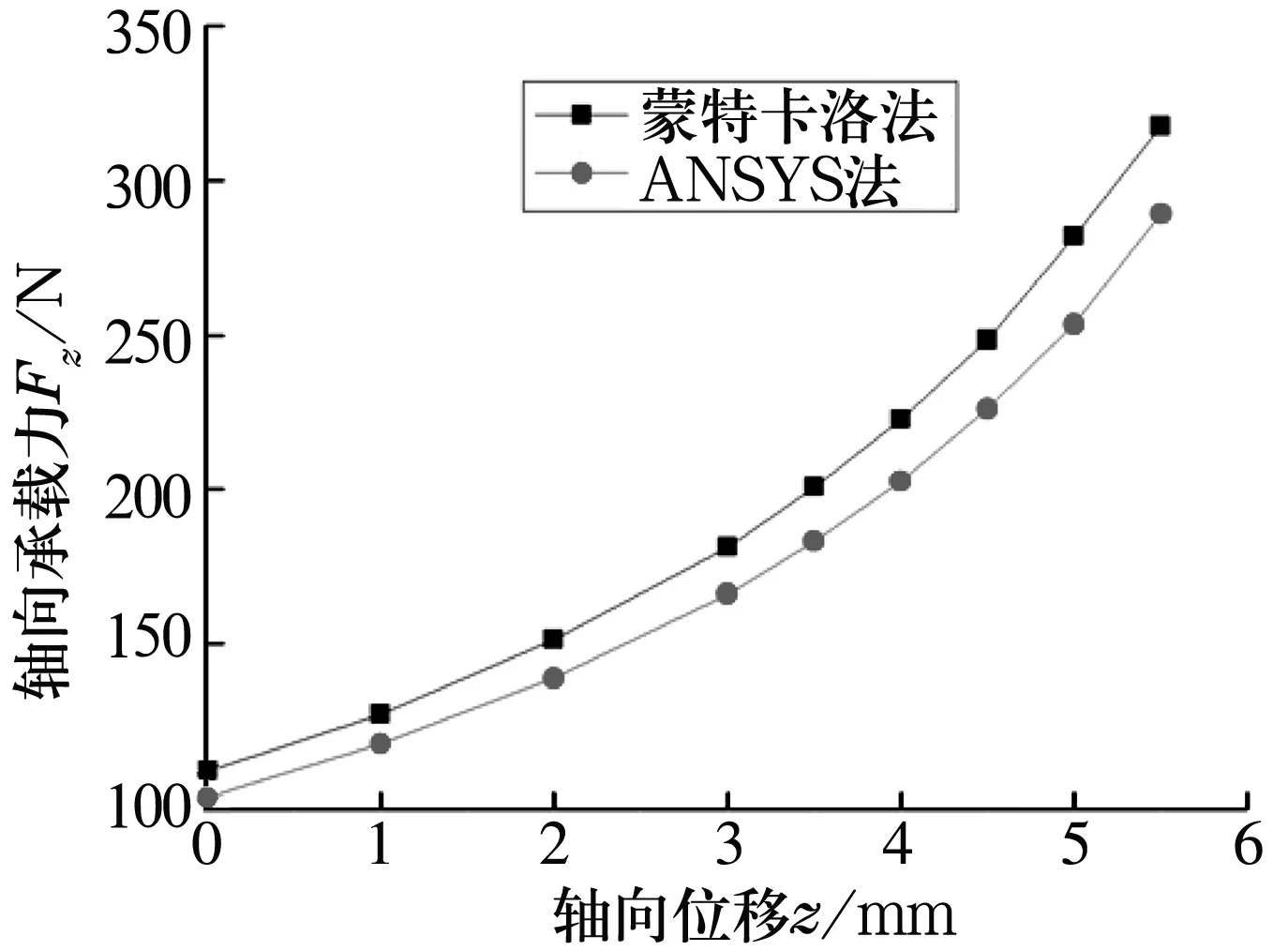
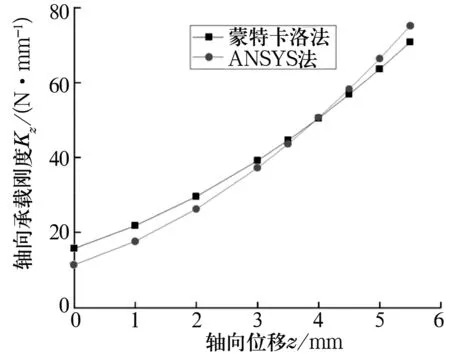
永磁軸承的基本結構如圖1所示,其中A為動磁環,B為靜磁環,c0為兩磁環間的初始氣隙。當與轉子固定的動磁環受到z軸正方向外力Fz作用時,將在沿z軸正方向上產生一軸向位移z(0 圖1 永磁軸承結構圖 圖2 動磁環A受力示意圖 依據等效磁荷理論[1],可建立面1和面3之間的磁力F13,z的解析式 dr1dr3dαdβ/{[(c0-z+2L)2+(r3cosβ-r1cosα)2+ (r3sinβ-r1sinα)2]3/2}; (1) 同理可建立面2和面4、面1和面4以及面2和面3的磁力F24,z,F14,z,F23,z的解析式 dαdβ/{[(c0-z)2+ (r4cosβ-r2cosα)2+ (r4sinβ-r2sinα)2]3/2}, (2) dαdβ/{[(c0-z+L)2+ (r4cosβ-r1cosα)2+(r4sinβ-r1sinα)2]3/2}, (3) dr2dr3dαdβ/{[(c0-z+L)2+(r3cosβ-r2cosα)2+ (r3sinβ-r2sinα)2]3/2}, (4) 式中:Br為磁環剩磁(假設兩磁環剩磁相同);μ0為真空磁導率;(r1,α),(r2,α),(r3,β),(r4,β)分別為面1,2,3,4上任一點的極坐標。 規定磁力正方向為坐標軸正方向,則軸向外載荷Fz為 Fz=F13,z+F24,z-F14,z-F23,z。 (5) 永磁軸承的剛度是指動磁環在受到外擾力時,抵抗偏離平衡位置的能力。因此可以定義永磁軸承軸向剛度Kz為 (6) 蒙特卡洛法求解多重積分的思想為任意一個積分都可看作是某個隨機變量的數學期望[8]。因此,在利用蒙特卡洛法計算多重積分時,采用隨機變量的算術平均值作為其近似值。 設D為n維空間Rn的一個區域,f(x)∈D?Rn→R,區域D上的n重積分用下式表示 (7) I可以被認為等于區域D的測度乘以函數f(p)的期望。計算時首先要選擇概率密度函數g(p1,p2,…,pn),并且在區域D內滿足g(p1,p2,…,pn)>0。 則(7)式可改寫為 dp1dp2…dpn。 (8) 無論區域D的形狀如何,根據概率密度函數g(p1,p2,…,pn)進行抽樣時(抽樣次數為N),均可以給出積分的估計為 (9) 標準差為 (10) (11) 積分誤差為 (12) 式中:Xα為與置信度1-α有關的參數,當α已知,可以查到相應的Xα;σ為標準差。 基本的蒙特卡洛法就是找一個包含區域D的超立方體(測度已知,為Mc),在D內隨機生成N(N一般足夠大)個均勻分布的點,統計落入區域D的點,假設有m個,則區域D的測度為 (13) 函數f的期望為 (14) 從而有 (15) 將(15)式應用到四重積分,可得 (16) 式中:bj為四重積分的4個積分上限;aj為對應的4個積分下限;j=1,2,3,4。 如圖3所示,按照圖示流程即可將(16)式用程序實現,求解磁力非常方便。 圖3 蒙特卡洛法計算磁力流程圖 采用Matlab進行編程,生成超立方體內的隨機數可以調用函數unifrnd,調用格式為[9]:unifrnd(積分下限,積分上限,1,N)。 值得注意的是,蒙特卡洛法是一種近似方法,是概率統計的方法,定義不同的N值,積分值不會相同。下面將通過定義不同的N值和多次求解磁力來探究N值對結果精度以及可重復性的影響。 對照圖1的軸承結構,文中計算所采用的尺寸為R1=10 mm,R2=20 mm,R3=10 mm,R4=20 mm,L=15 mm,初始軸向氣隙c0=6 mm。定義永磁環性能參數:Br=1.231 T,Hc=917 530 A/m,則磁環的相對磁導率μr為 (17) 將上述參數代入到等效磁荷法公式中,編制程序進行求解。 其他參數均不變,改變N值得出的永磁軸承磁力曲線如圖4、圖5所示。 圖4 改變N值時磁力曲線變化示意圖 圖5 不同N值時z=4 mm處的磁力曲線(重復運行程序6次) 從圖4可以看出,隨著N值的減小,磁力曲線波動越來越大,曲線越來越不平滑,計算數值準確性隨之大大降低;并且積分區域越大,蒙特卡洛法的計算精度越低,因此,當磁環面積較大時,應該提高抽樣數量N。 從圖5可以看出,隨著N值的減小,數據的可重復性差;蒙特卡洛積分誤差與抽樣數的平方根成反比,在滿足工程應用(誤差在10%以內)的前提下,N應取一合適值(106)。 研究表明,在計算永磁軸承的承載能力時,有限元數值解是較為準確的[2-3,10]。用ANSYS求解時,若只考慮軸向氣隙的變化,采用軸對稱二維模型,單元類型選擇plane53,磁環網格尺寸為0.1 mm,空氣網格尺寸為2 mm,給最外層空氣邊界施加通量平行條件(即Az=0),將動磁環定義為一個組件,求解即可得到磁力線分布和軸向力的值。 圖6和圖7分別為蒙特卡洛法(N=1 000 000)與有限元數值解法的軸向力和軸向剛度計算結果對比。 圖6 軸向力與軸向位移關系曲線 由圖可以看出,兩種算法的計算結果接近,兩者的磁力值最大偏差對應的軸向偏移在5.5 mm附近,誤差約為6.5%。在最常使用的軸向偏移4 mm處,偏差僅為5.3%。軸向剛度與軸向位移關系曲線的變化趨勢比ANSYS得出的更平緩。 綜合圖6和圖7中的對比結果可知,蒙特卡洛法完全可以應用到永磁軸承的工程設計中。 圖7 軸向剛度與軸向位移關系曲線 (1)通過蒙特卡洛法與有限元數值解的結果比較可知,采用蒙特卡洛法結合等效磁荷法能夠較準確地計算出軸承的磁力以及剛度。 (2)在用蒙特卡洛法求解時,抽樣樣本N值越大,計算精度越高,但N值過大會增加計算周期,N值的選取應該使得磁力反復求解的波動不超過1%。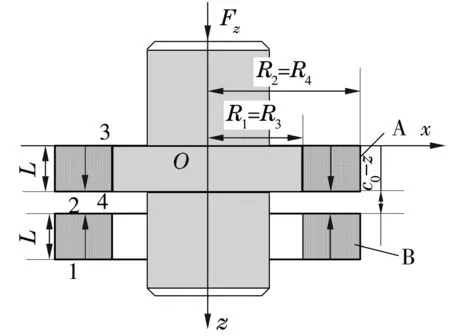
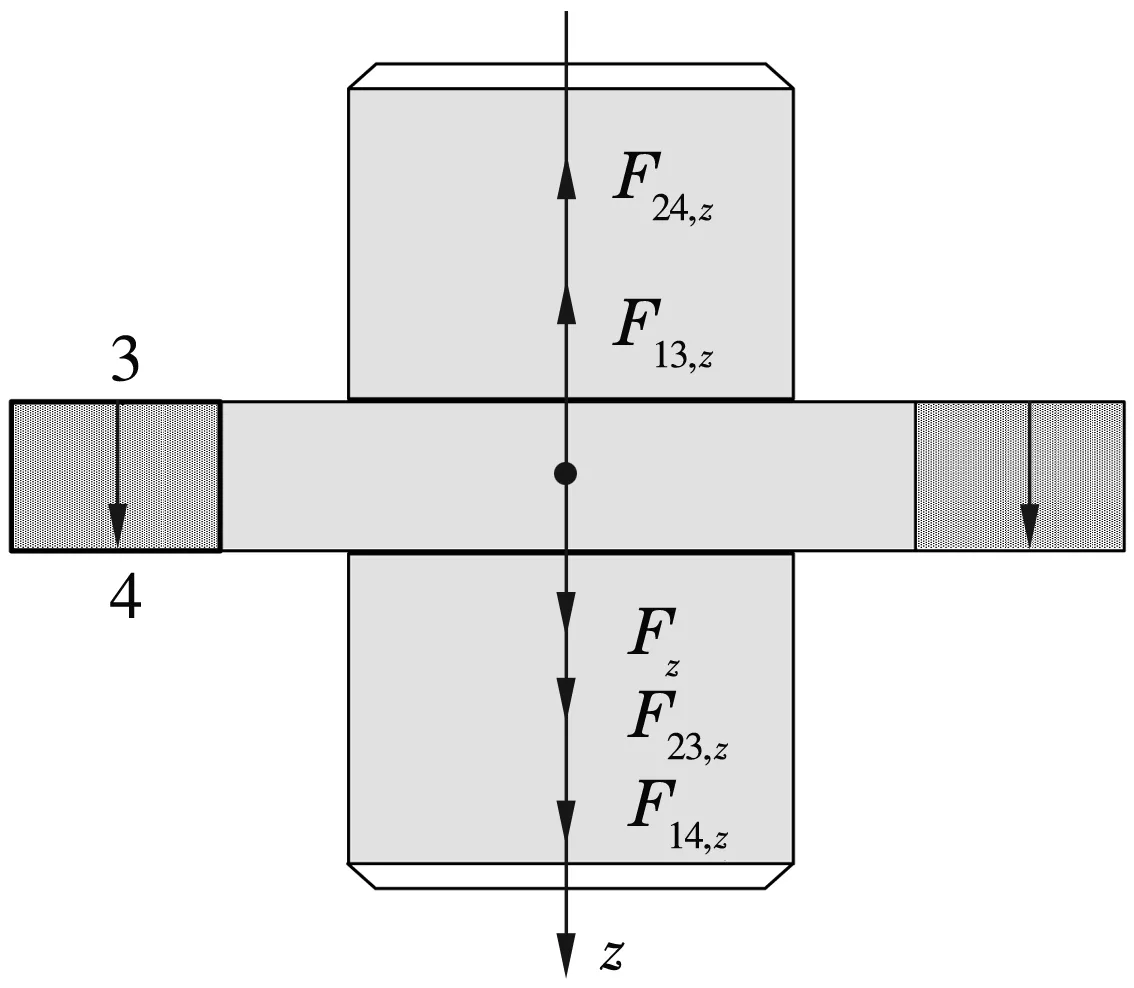
2 蒙特卡洛法對磁力的求解
2.1 基本蒙特卡洛積分法
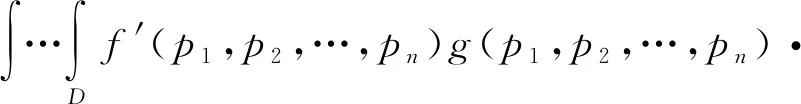
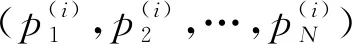
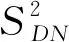
2.2 磁力的求解流程
3 永磁軸承磁力計算分析
3.1 樣本數量N對磁力值的影響
3.2 蒙特卡洛法與數值解法對比
4 結論

