確定Sn的元素的階的集合On的第一種方法

孫宗明

(泰山學院 數學系，山東 泰安 271000)

本文中，n 是正整數，Sn是n次對稱群，On是Sn的元素的階的集合，先討論On的構造，而后給出確定On的第一種方法和例子，并且，研究與數論的聯系.

1 On的構造(Ⅰ)

先列出兩個引理.

引理1 每一個n 元置換都可以分解為互不相連的循環置換的乘積，n個文字中的每個文字都出現于一個循環置換中，并且，不計因子次序時，分解式是唯一的.

證明 見［1］，定理，從略.證完.

引理2 設n 元置換π分解為s個互不相連的循環置換的乘積，它們的長度分別為n1，n2，…，ns，則π的階為n1，n2，…，ns的最小公倍數，即

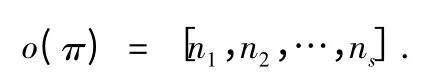
證明 見［2］，P63，定理5.1.2，從略.證完.

下面的定理給出了On的構造.

定理 Sn的元素的階的集合

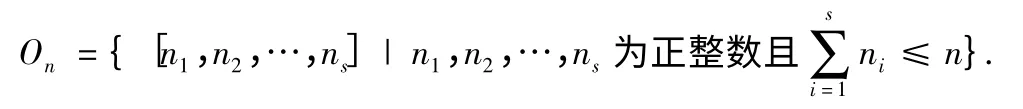
證明 首先，對于任意的

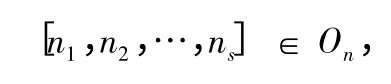
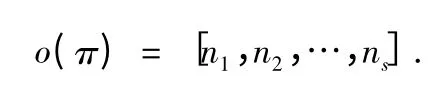
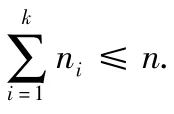
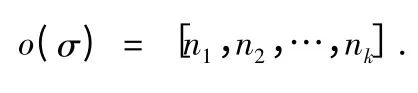
因此，o(σ)∈On.證完.

2 確定On的方法(Ⅰ)和例子

因為，求一組整數的最大公因數時，若整數組中有重復的數，則可以從重復的數中任取一個數而去掉其他的，所以，根據定理，就得到下面的確定On的第一種具體方法.

方法(Ⅰ)按下列5個步驟確定集合On:

1)求出k，使1+2+…+(k－1)+k ≥n，而1+2+…+(k－1)＜n;

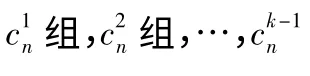
4)計算〈n1，n2，…，ns〉中的n1，n2，…，ns的最小公倍數;

5)上步中的所有的數就構成On.

應該注意，這里的［n1，n2，…，ns］僅僅作為數組的記號，并不表示最小公倍數，下面的一些地方也是這樣.

下面給出兩個例子.

例1 當n=5 時，

1)因1+2+3 ＞5，而1+2＜5，所以k=3;

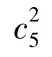
3)〈1〉，〈2〉，〈3〉，〈4〉，〈5〉，〈1，2〉，〈1，3〉，〈1，4〉，〈2，3〉;

4)上面的9個數組的最小公倍數分別是1，2，3，4，5，2，3，4，6;

5)O5={1，2，3，4，5，6}.

當n=6 時，

1)因1+2+3=6，而1+2＜6，所以k=3;

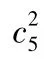
還有一組:［1，2，3］;

3)〈1〉，〈2〉，〈3〉，〈4〉，〈5〉，〈6〉，〈1，2〉，〈1，3〉，〈1，4〉，〈1，5〉，〈2，3〉，〈2，4〉，〈1，2，3〉;

4)上面的13個數組的最小公倍數分別是1，2，3，4，5，6，2，3，4，5，6，4，6;

5)O6={1，2，3，4，5，6}.

同樣，可以繼續確定On，列出下面的結果，具體步驟均從略.

當n=7 時，O7={1，2，3，4，5，6，7，10，12}.

當n=8 時，O8={1，2，3，4，5，6，7，8，10，12，15}.

當n=9 時，O9={1，2，3，4，5，6，7，8，9，10，12，14，15，20}.

當n=10 時，O10{1，2，3，4，5，6，7，8，9，10，12，14，15，20，21，30}.

關于O1至O4，容易得到，列出結果如下，具體步驟也從略.

O1={1}，O2={1，2}，O3={1，2，3}，O4={1，2，3，4}.

關于On中元素的個數| On|，由上可得:| O1|=1，| O2|=2，| O3|=3，| O4|=4，| O5|=6，| O6|=6，| O7|=9，| O8|=11，| O9|=14，| O10|=16.

例2 列出下面的結果，具體步驟從略.

O9=O8∪{9，14，20}，| O9|=14;

O10=O9∪{21，30}，| O10|=16;

O11=O10∪{11，18，24，28}，| O11|=20;

O12=O11∪{35，42，60}，| O12|=23.

3 數論函數

用數論的語言，定理表述為下面的

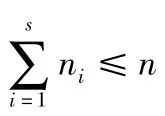
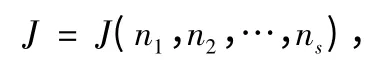
所有的J 構成集合SJ.試確定SJ.

問題2 集合SJ的元素的最大值記為J(n)，試求J(n).能否找到J(n)的表達式?

實際上，J(n)是一個數論函數，尋找用n的式子來表示J(n)，值得從數論的角度進行探討.

［1］孫宗明.元置換的分解［J］.益陽師專學報(自然科學版)，1987(1):29－31.

［2］［美］M.赫爾著，裘光明譯.群論［M］.北京:科學出版社，1982 ﹒

［3］孫宗明.次對稱群的元素的階的集合［J］.數學的實踐與認識，1983(3):25－26(美國，Math.Reviws，1985(e):20007).

［4］孫宗明.關于的元素的階的集合［J］.內蒙古師大學報(自然科學漢文版)，1994(2):13－17(美國，Math.Reviws，1995年索引，P1321，P396).

［5］孫宗明.有限阿貝爾群同構的一個判定算法［J］.商丘師范學院學報，2004，20(2):53.

［6］孫宗明.關于階群的子群個數的若干結論［J］.商丘師范學院學報，2008，24(3):44－45.

［7］孫宗明.關于極大子群的若干結果［J］.商丘師范學院學報，2010，26(3):27－28.

［8］孫宗明.群的階方程及其應用［J］.內蒙古師大學報(自然科學漢文版)，2010(39):462－466.

［9］孫宗明.循環群的子群交子群并子群積的構造［J］.商丘師范學院學報，2011，27(3):26－28.