電勵磁雙凸極電動機換相轉矩脈動的研究

鄒治銳，陳世元

(華南理工大學，廣東廣州510640)

0 引 言

電勵磁雙凸極電動機(以下簡稱DSEM)類似雙凸極永磁電機，具有結構簡單、控制靈活、力矩電流比大、功率密度高等優點，在航空電源、風力發電、電動汽車等領域有著廣闊的應用前景［1－2］。DSEM同樣無法避免磁阻類電機所存在的轉矩脈動問題。

DSEM轉矩脈動產生的原因有多方面，主要源于兩種情況:一種是電磁因素造成的轉矩脈動，通電繞組電流并不是理想的方波電流，會導致電磁轉矩存在原理性波動［3］;另一種是電流換向產生的轉矩脈動，對輸出轉矩的影響比較大［4］。本文重點分析在通電狀態改變下換向電流的變化過程，研究換相轉矩脈動產生的原因，為DSEM電機的轉矩優化提供一定的參考意義。

1 電機結構原理

圖1是一臺三相15 kW、12/8極外轉子DSEM輪轂電機剖面圖。A、B、C三相電樞繞組和勵磁繞組均放置在定子上，轉子上沒有繞組。選擇其中4個沿圓周均勻分布且空間相對的定子槽，加深其深度和寬度以放置勵磁繞組［5］。

圖1 DSEM輪轂電機剖面圖

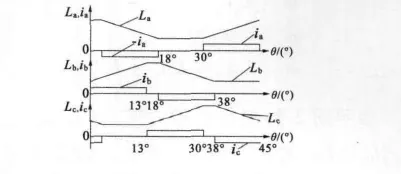
圖2 理想電感波形與電流波形

設計DSEM電機一般采用開關磁阻電動機的設計原則，選擇轉子極弧略大于定子極弧，這是為了保證在任何轉子位置時均具有正、反向自起動能力以及相繞組的換流［6－7］，本文轉子極弧取 18°。理想的電感波形與電流波形如圖2所示，根據電感上升區間通正電流、電感下降區間通負電流、電感不變區間不通電的原則，故通電模式為三相六狀態，有些類似于無刷直流電動機的通電模式。三相繞組為星形連接，主電路采用全橋控制電路，如圖3所示。

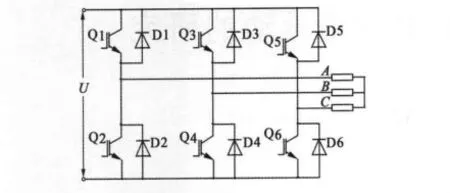
圖3 全橋控制電路

2 換相轉矩脈動分析

2.1 B+C－相導通向B+A－相導通換相過程

參照圖2的通電規律，分析B+C－相導通向B+A－相導通換相過程:開關Q3保持開通狀態不變，B相繞組電流持續，Q6關斷的同時Q2開通，A相繞組電流由零開始負向上升，由于電感的存在，C相繞組不能馬上變為零，而是通過與二極管D5續流，等效電路如圖4所示。

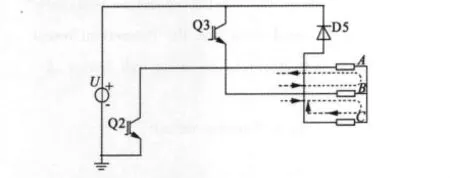
圖4 B+C－向B+A－換相等效電路

假設繞組電感忽略不計，B+C－導通向B+A－導通換相瞬間，有 eb= －ec=E，ea=0，U=eb－(－ec)=2E，故電壓平衡方程式:

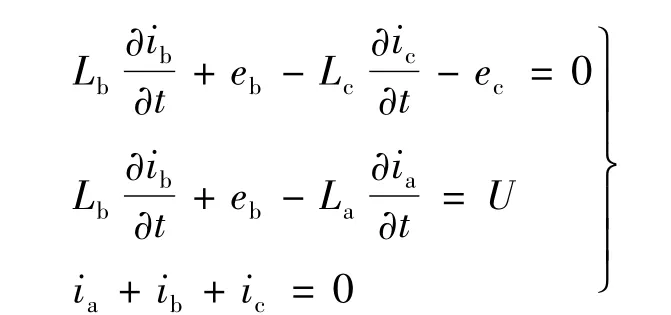
解上述方程組得:

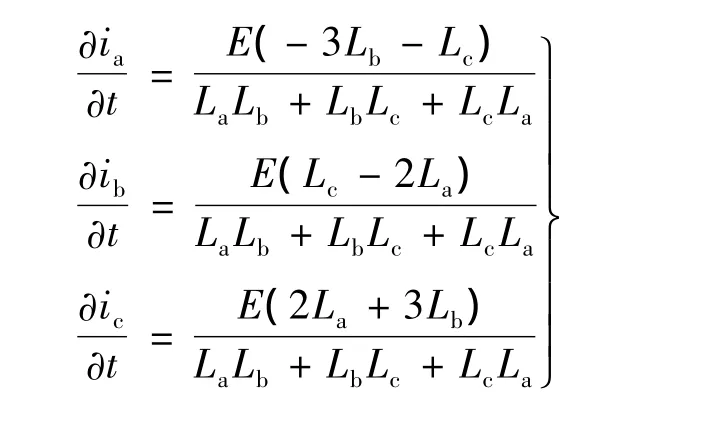
參照圖2的理想電感波形，有La=Lmax，Lc=Lmin，Lb比Lmin大一些，令 Lb=L2nd，則方程組可改為:

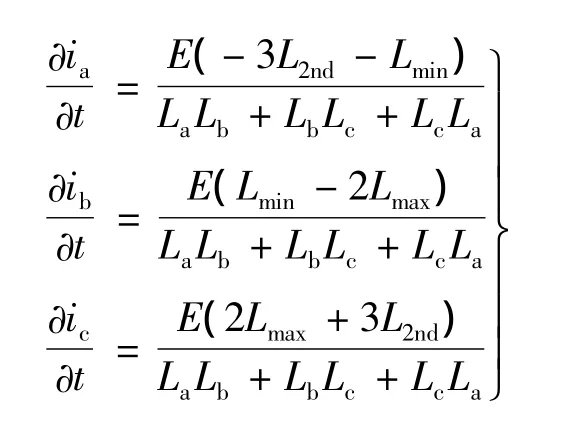
2.2 B+A－相導通向C+A－相導通換相過程

分析B+A－相導通向C+A－相導通換相過程:開關Q2保持開通狀態不變，A相繞組電流持續，Q3關斷的同時Q5開通，C相繞組電流由零開始上升，由于電感的存在B相繞組不能馬上變為零，而是通過與二極管D4續流，等效電路如圖5所示。

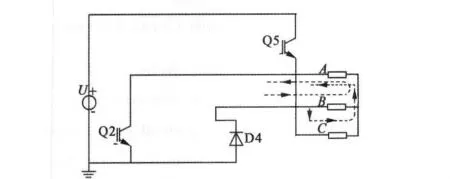
圖5 B+A－向C+A－換相等效電路

同理，B+A－導通向C+A－導通換相瞬間，有eb= －ea=E，ec=0，U=eb－(－ea)=2E，故電壓平衡方程式:

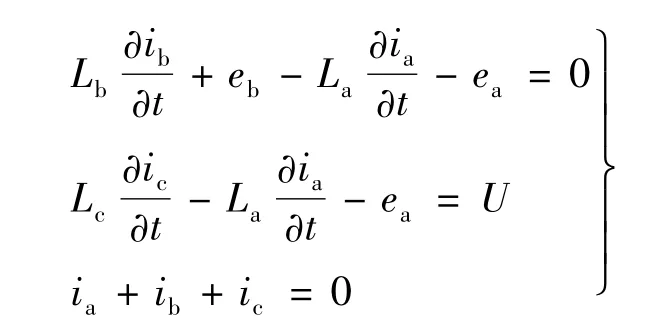
解方程組得:

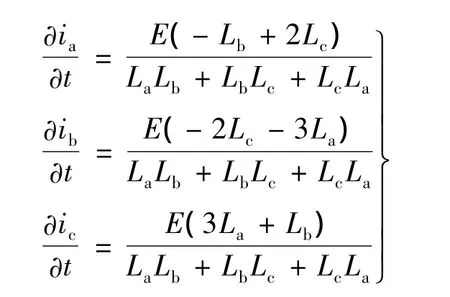
同理有 Lb=Lmax，Lc=Lmin，La比Lmin大一些，令La=L2nd，則方程組可改為:

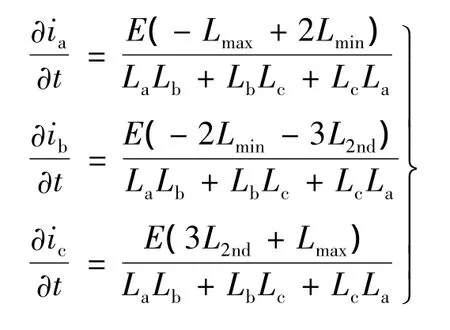
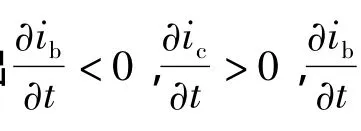
可以看出的正負性不明顯，換向相B相處于電感不變區間理論上不產生轉矩;換向相C相的電流從零開始正向上升;一般情況下，DSEM中最大電感值要大于兩倍的最小電感值，故非換向相A相的電流變化率偏小于零，因為A相為負電流，電流會繼續負向增大，但由于電流滯環控制電路的作用使得電流不會繼續增大，故A相電流可以保持在穩定的范圍內。

3 仿真結果分析與改善

利用ANSOFT公司開發的電磁場有限元分析軟件Maxwell和ANSOFT公司的另一款電路仿真軟件Simplorer進行聯合仿真，搭建橫跨電場與磁場的耦合場瞬態仿真模型，實現電路、控制、磁場三方的同時仿真，具有較高的仿真精度，非常適合電機控制系統的仿真分析。

在Maxwell中建立DSEM電機模型，在Simplorer中加入全橋電路及電流滯環控制電路，得到的三相電流仿真波形如圖6所示。可以看出B+C－向B+A－換相時非換向相B相電流有明顯的下降，即使有電流滯環電路也阻擋不了電流下降的趨勢;換向相A相電流變化的時間要比C相長一些，均與理論分析吻合。

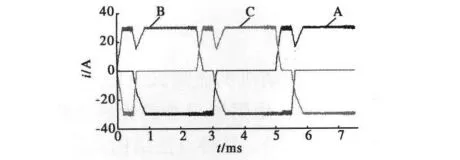
圖6 三相電流波形

圖7 是輸出轉矩曲線圖，電流換向時電流未達到穩定電流參考值，使得轉矩出力變小，從而輸出轉矩形成凹陷，產生脈動。

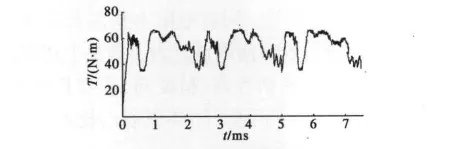
圖7 轉矩曲線

由于三相繞組是星形連接，在全橋電路控制下，換向相電流的變化易引起非換向相電流的變化，圖6已經表明這種情況。

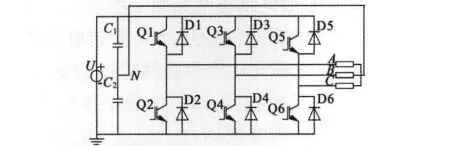
圖8 半橋控制電路

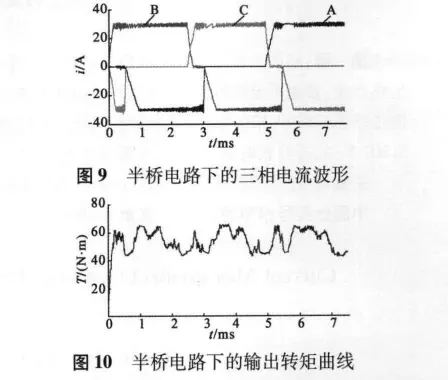
圖8 是半橋控制電路引入電容的中點電位，使三相繞組工作互不干擾，有利于獨立控制［8］。在電流滯環控制下，三個繞組無需限制在ia+ib+ic=0的條件下，非換向相電流很好地控制在一個波動較小范圍內，三相電流波形如圖9所示。非換向相電流凹陷的消除使得輸出轉矩脈動有所減小，如圖10所示。

半橋控制電路有一定的局限性，要求分裂式電容充放電保持平衡，維持中性點電壓穩定，則需要某一換向相繞組電流反向(正到負或負到正)達到給定值，另一換向相恰好關斷完畢［8］(電流為零)，因而圖2中傳統的通電方式需要進行角度優化，以滿足電容充放電平衡。

4 結 語

理想的方波電流才能產生較為平穩的轉矩，通過分析從一個通電狀態到另一個狀態換向電流瞬間變化的過程，研究換相轉矩脈動產生的原因，換向相電流正向上升到正的穩定電流參考值或負向上升到負的穩定電流參考值需要一定的時間，非換向相電流的凹陷都對換相轉矩脈動產生影響，軟件仿真驗證了結論的正確性。

與全橋電路相比，半橋電路消除了換向過程中非換向相電流產生的凹陷，很好地保持非換向相電流的穩定，對轉矩脈動有一定的改善，但要求滿足電容充放電平衡，否則電容的中性點電壓不易穩定，因而需要角度優化控制，通過調整開關管的通斷區間來維持電容充放電平衡。

［1］孔祥新，程明，束亞剛，等.定子雙饋電雙凸極電動機轉矩脈動分析與抑制［J］.電工技術學報，2008，23(5):18 －22.

［2］張樂.電勵磁雙凸極電機轉矩脈動分析與抑制［J］.中國電機工程學報，2010，30(3):83 －89.

［3］譚建成.永磁無刷直流電機技術［M］.北京:機械工業出版社，2011，3:177 －178.

［4］相蓉，周波，孟小利.電勵磁雙凸極電機轉矩脈動分析與抑制［J］.南京航空航天大學學報，2001，33(4):366 －371.

［5］余海闊，陳世元.電勵磁雙凸極輪轂電機空載性能的有限元分析［J］.微電機，2011，44(6):23 －26.

［6］李永斌，龔宇，江建中.雙凸極永磁電機斜極轉子設計和繞組換流模式研究［J］.電工技術學報，2005，20(7):70 －75.

［7］李永斌.定子雙饋雙凸極永磁電機及其控制系統研究［D］.上海:上海大學，2004，6.

［8］李國生.基于半橋變換器的電勵磁雙凸極電機角度優化控制策略［J］.中國電機工程學報，2011，31(27):102 －108.