PWM整流器直接功率控制系統的優化設計

劉曉艷，盧健康，馬 艷

(西北工業大學，陜西西安710072)

0 引 言

三相電壓型PWM整流器具有單位功率因數、直流電壓大小可調、動態性能良好以及可實現能量的雙向流動等優點，符合“綠色電能變換”潮流，也是治理諧波和“無功”污染最根本的措施之一，因此得到了廣泛研究與應用［1］。

本文首先簡介了三相電壓型PWM整流器主電路的拓撲結構，接著介紹了其DPC系統構成;然后在文獻［1］所述DPC系統的基礎上，改進了電壓外環結構—— 將慣性濾波環節從前向通道移到了反饋回路中，與文獻［1］原來的濾波環節設計相比，加快了系統的跟隨性指標。另外，為了提高系統的穩定性和動態性能，本文將原來電壓環的PI調節器改為PID調節器，再利用最平幅頻法［6］設計該電壓調節器的PID參數，使得系統動態性能得到優化，也實現了單位功率因數控制(動態過程結束后無功功率穩定在零值附近)。MATLAB/Simulink仿真驗證結果表明，DPC系統的優化設計方案可行并且能使DPC系統性能更好。

1 三相電壓型PWM整流器直接功率控制系統簡介

1.1 三相電壓型PWM整流器的主電路結構與數學模型

三相電壓型PWM整流器(VSR)主電路拓撲結構如圖1所示。圖中uj(j=a、b、c)為電源相電壓;ij(j=a、b、c)為三相線電流;Sj(j=a、b、c)為整流橋的開關函數;udc為直流電壓;L為濾波電抗器的電感;R為交流側濾波電抗器的等效電阻和功率管的開關損耗等效電阻之和;C為直流側電容;RL為負載電阻［2］。

圖1 三相電壓型PWM整流器主電路拓撲結構圖

假定三相交流電壓對稱，則由圖1可得三相靜止坐標系下的三相電壓型PWM整流器的數學模型。

定義Sj(j=a、b、c)為單極性二值邏輯開關函數，其中:

1.2 三相電壓型PWM整流器系統結構及工作原理

三相電壓型PWM整流器主要由主電路和控制電路組成，主電路結構如圖1所示。整個系統結構如圖2所示。控制電路采用直流電壓外環和功率內環構成雙閉環結構。根據瞬時功率理論，可以在線實時計算出期望的系統瞬時有功功率和無功功率(期望的系統瞬時無功功率值為零)，然后與根據交流電壓與交流電流實時計算的實際有功功率和無功功率進行比較，將比較的結果送入滯環比較器中，最后依據交流電壓矢量所在的扇區與功率滯環比較器輸出結果，從事先設計并儲存的開關矢量表中選擇出所需的三個開關量sj。此控制方法不僅能有效控制有功功率的變化，而且使得穩態時瞬時無功功率基本為零，從而使整流器在單位功率因數條件下工作。

圖2 三相電壓型PWM整流器DPC系統結構

本文在線檢測和計算實際瞬時有功功率和無功功率時采用文獻［3］推導出的公式:

與文獻［1］采用的檢測和計算方法相比，不僅可以只用兩個交流電壓傳感器與兩個交流電流傳感器以減少硬件、節約成本，而且避免了三相到兩相的靜止坐標變換，減少了實時計算工作量。另外，采用這種方法不僅適于三相電壓對稱的情況，也適于三相電壓不對稱的情況。因為無論三相電壓是否對稱，三個線電壓之和與三個線電流之和總是零。

2 三相電壓型PWM整流器電壓環的結構及其改進

文獻［1］給出的三相電壓型PWM整流器DPC系統的電壓環結構如圖3所示。

圖3 文獻［1］的電壓環結構圖

該電壓環由前向通道的5個環節串聯而成，分別為慣性濾波環節GLF、PI調節器、作為比例環節的直流電壓給定值Udcr、由功率內環近似等效成的小慣性環節Gp(s)和主電路直流側電阻電容及直流電壓給定值構成的大慣性環節Go(s)。各個環節的傳遞函數表達式如下:

其中的慣性濾波環節本來是為了濾除直流電壓反饋值中的紋波，但由于把該環節放在反饋通道中時無法按照“工程設計法”［5］來設計調節器參數，所以才把它移到了前向通道中。然而，這樣一來就相當于分別在電壓反饋通道與給定通道都加了同樣的慣性濾波環節，實際上延緩了電壓給定信號，降低了系統響應的跟隨性能指標。

為了克服文獻［1］給出的上述電壓環結構所帶來的系統響應跟隨性能指標降低的缺陷，本文把慣性濾波環節放在反饋通道中，同時為了提高系統的動態性能，將電壓調節器改為PID調節器，然后按照文獻［6］提出的“有零點典型I型系統”結構和相應的調節器參數優化設計方法—— 最平幅頻法來優化設計調節器參數。其電壓環結構如圖4所示。

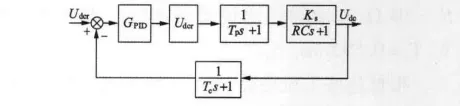
圖4 改進的電壓環結構圖

3 三相電壓型PWM整流器電壓調節器的優化設計方法

為了提高系統的動態性能，我們將電壓環調節器的結構由文獻［1］中給出的PI調節器改為PID調節器，其傳遞函數:

由圖4可得到該控制系統電壓環的開環傳遞函數為:

根據零極點對消法［6］，先用電壓調節器中的一個零點對消掉時間常數Go(s)中的大慣性，即取τ1=RLC。為了使本方法具有通用性和設計更方便，以Tp為時間基準，將參數進行歸一化處理，亦即，令P=Tps，進行復變量代換，則系統的電壓環結構如圖5所示。圖中:

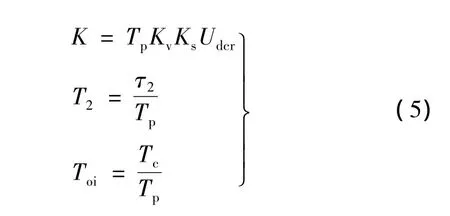
圖5 電壓環結構圖

根據設計“有零點典型I型系統”的最平幅頻法，K 和 Toi的函數關系［6］:

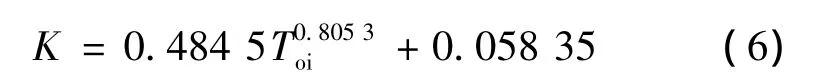
取 Toi=1.1，可以求得:K=0.581 7。

再根據設計這種類型系統的最平幅頻法中K、Toi和 T2的函數關系式［6］:

不難求得:T2=1.531 3。

4 三相電壓型PWM整流器DPC系統仿真

為了驗證上述對電壓環的結構改進和調節器優化設計的正確性，我們按照圖2的系統結構和下述系統參數采用MATLAB/Simulink軟件在電路級進行了仿真。系統參數:三相電源相電壓峰值100 V，頻率50 Hz，交流側電感L=10 mH，直流側電容C=1 100 μF，輸出直流電壓給定值Udcr=200 V，負載電阻RL=50 Ω，功率滯環比較器滯環寬度Hq=Hp=200 W，Tp=0.592 ms。

根據這些系統參數，由式(5)～式(7)可以計算出PID 調節器參數:Kv=19.65，τ1=55 ms，τ2=0.94 ms。

用Simulink仿真的波形如圖6～圖8所示。其中圖6(a)為按照文獻［1］方法設計電壓環得出的直流側電壓的波形，而圖6(b)為按照本文方法優化設計電壓環后得出的直流側電壓的波形;圖7為按照本文方法優化設計后得出的網側A相相電壓(圖中的純正弦波)和相電流波形;圖8為按照本文方法優化設計后得出的瞬時有功功率(圖中峰值較低的波形)和瞬時無功功率波形。

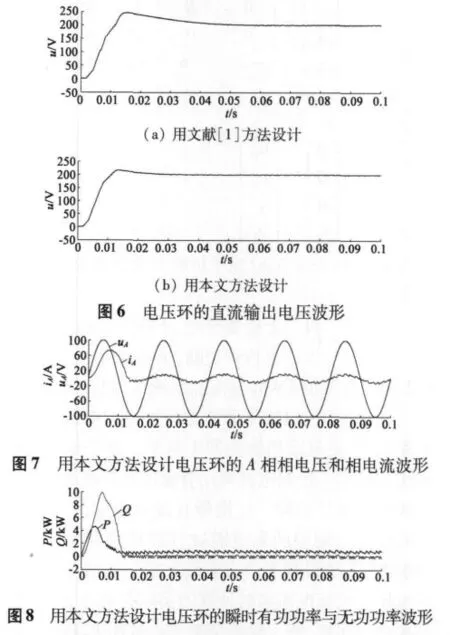
通過圖6(a)和6(b)的比較可以看出，采用本文的優化設計方法改進電壓環后，系統的動態性能得到顯著改善:圖6(a)中階躍響應的超調量σ=22.165%，圖 6(b)中階躍響應的超調量 σ=7.865%;圖 6(a)中調節時間 ts=37.35 ms，圖6(b)中調節時間ts=17.35 ms(計算調節時間以±5%為穩態誤差限)。可見，改進電壓環設計后，超調量只有原來的三分之一左右，而調節時間還不到原來的一半。圖6中兩個直流輸出電壓在穩態時都穩定在給定參考電壓200 V。另外，需要補充的是，文獻［1］中的電壓環盡管是按照典型Ⅱ型系統設計的，但由于其中的第2個積分環節是用大慣性環節近似而成，所以，其穩態誤差度與本文方法設計的電壓環一樣，仍然是Ⅰ而非Ⅱ。

由圖7和圖8可以看出，按照本文方法優化設計電壓環后，在過渡過程結束后，也實現了三相電壓型PWM整流器的網側電流正弦化且交流相電壓與相電流同相，瞬時無功功率穩定在零值附近，系統工作于單位功率因數情況下，瞬時有功功率值穩定在給定值800 W附近。綜上所述，仿真結果表明本文的系統電壓環優化設計方法可行，且會使系統具有更好的動態性能。

5 結 語

本文對傳統的采用DPC策略的三相電壓型PWM整流器的電壓外環和功率內環(采用滯環比較器控制)控制策略做了兩點改進:一是把電壓環的慣性濾波環節從前向通道改到了反饋回路中，借以提高系統的快速跟隨性能;二是利用最平幅頻法優化設計了電壓調節器的結構和參數。通過Simulink系統仿真對上述兩點改進措施進行了檢驗，結果表明:采用DPC策略的三相電壓型PWM整流器具有調節時間短、超調量小和仍保持單位功率因數等優點。

［1］王久和.電壓型PWM整流器的非線性控制［M］.北京:機械工業出版社，2008.

［2］王久和.電壓型PWM整流器直接功率控制系統［J］.中國電機工程學報，2006，26(18):54 －60.

［3］盧健康，邢益巽.PWM整流器直接功率控制策略仿真研究［J］.計算機仿真，2012(8):299 －303.

［4］高揚.電氣傳動自動控制系統優化設計方法研究［D］.西安:西北工業大學，2006.

［5］陳伯時.電力拖動自動控制系統［M］.北京:機械工業出版社，2003.

［6］盧健康，王澤峰.雙閉環調速系統設計方法的改進及其仿真［J］.系統仿真技術，2010，6(1):29 －32，58.