汽車發電機變化氣隙磁導模型的建立

鮑曉華，劉謀志

(合肥工業大學，安徽合肥230009)

0 引 言

爪極電機由于制造簡單、成本低而廣泛應用于各種領域，特別是在汽車工業、新能源發電及國防科技領域得到日益廣泛的應用［1］。隨著爪極電機功率密度的增加和環境要求質量升級，準確把握其電磁噪聲機理及控制技術倍受國內外學者的關注。

在電機相關電磁性能的研究中，氣隙磁導作為影響氣隙磁場和感應電勢的關鍵因素，對其進行準確的求解一直都是電機設計及電磁性能優化的關鍵環節。文獻［2］在進行永磁電機的空載磁場分布的計算時，著重針對開槽的氣隙表面，應用保角變換的槽幾何分析了開槽對其氣隙磁導的影響，對永磁電機開槽的氣隙磁導作出了比較全面的分析，保證了永磁電機電磁性能的進一步分析更為精確;文獻［3］在考慮感應電動機磁路飽和時，針對其飽和模型的建模分析應用氣隙磁導的變化來反應模型磁路飽和的改變，并證明了該模型的有效性;文獻［4］針對電機電樞繞組內部故障的分析中，考慮到可以應用氣隙磁導模型分析計算其磁路的改變，對故障進行模擬和分析。因此其中所建氣隙磁導模型的準確性直接關系到對故障的反應的準確性;文獻［5－7］中針對表貼式永磁電機建模分析其氣隙磁導模型，在此基礎上分析了其氣隙磁場的分布，進行了感應電勢的計算，且討論了氣隙磁密分布對齒槽轉矩的影響。文獻［8］對凸極同步電機的非均勻氣隙進行了氣隙磁導模型的分析與研究，推導了任意轉子機械角位移下氣隙磁導的計算方法。這些文獻的研究中，為了更加準確地計算各種電機的氣隙磁場及與其相關的電磁性能，針對各種電機建立了相應的氣隙磁導模型，對不同電機的氣隙磁導在不同電機結構時的分析計算作出了相應的貢獻，使得相應電機的氣隙磁場的分析計算更為準確，為電機性能的提高與優化提供了研究基礎。

通過研究發現，爪極以懸臂梁方式在電磁激振力、旋轉離心力復合作用下產生機械形變，進而引起氣隙磁導的變化;爪極電機由于氣隙磁導的變化導致氣隙磁密和電磁激振力的脈動，進而引起定子軛按不同模態振動是產生電磁噪聲的關鍵因素之一。在以往的汽車用爪極發電機的氣隙磁場的計算研究過程中，甚少有涉及到其氣隙磁導的分析計算，也一直認為氣隙磁導在爪極電機運行過程中保持不變，這也是傳統電磁噪聲理論在爪極電機應用上往往被忽視的關鍵問題之一。隨著現代汽車對發電機性能要求越來越高，這顯然已經不能滿足高性能汽車發電機的設計與性能優化。基于此，本文將著重研究在電磁激振力、旋轉離心力復合作用下引起的氣隙磁導變化的分析建模，且分析計算由于氣隙磁導變化而導致的氣隙磁密波形脈動對電機性能的影響。

1 汽車發電機變化氣隙磁導模型建立的基本電磁理論分析

由于汽車發電機是一種特殊結構的凸極同步電機，因此基于汽車發電機的氣隙磁導的求解可以參考傳統凸極同步電機的氣隙磁導的求解方法。考慮汽車發電機特殊的轉子結構，應用有效合理的等效手段，顯然可以對汽車發電機的氣隙磁導進行比較精確的求解。與此同時，為汽車發電機的相關性能的提高和優化提供更為科學的計算方法。

等效于傳統凸極同步電機，在汽車發電機中，當A相繞組中通以正弦電流iA時，iA將產生正弦分布的脈振磁動勢fA，其幅值FA位于A相繞組的軸線處:

應用雙反應理論，將fA分解為直軸分量fAd和交軸分量fAq，則直軸和交軸磁動勢的幅值FAd和FAq應分別為:

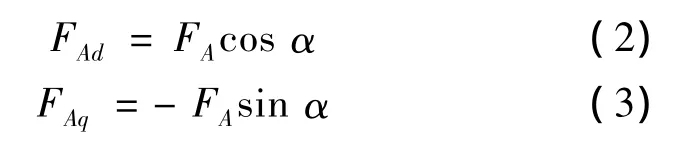
式中:α為轉子直軸與定子A相軸線間的夾角(以電角度記)。

電機中的氣隙磁導決定于定、轉子槽，定、轉子間的不同心度，定、轉子形狀不對稱及磁路的飽和情況。參考理想的凸極同步電機，以直軸作為坐標原點時，在距離原點θ電角度處，單位面積的氣隙磁導λδ可以精確地表示:

式中:λδ0為比磁導的平均值;λδ2為比磁導的二次諧波幅值。

則在汽車發電機氣隙磁場中，標量磁位解出后，氣隙內各點磁感應強度的法向分量Bn即可求出，其中:

氣隙內某一點的比磁導(即單位面積的磁導)λ定義:

F(x)為作用于氣隙的磁勢。設δ為氣隙長度，λB為恒定磁勢作用下的均勻氣隙時的比磁導，λB=，以λB為基值，比磁導的標幺值即:

因此在汽車發電機中，當轉子爪極受旋轉離心力和電磁激振力而向外彎曲時，即氣隙δ沿爪極軸向變化時，則需將上式中δ改為δ(x)，即可得變化的氣隙比磁導:

汽車發電機在不同運行轉速、不同發電頻率，即轉子爪極所受旋轉離心力和電磁激振力大小改變時，轉子爪極也會相應有不同程度的向外偏心形變。因此，汽車發電機的氣隙磁導在整個發電機的運行轉速曲線上都會隨運行轉速的不同而變化。因而，基于氣隙磁場計算的汽車發電機各種電磁性能的研究顯然需要更為精確的變化的氣隙磁導模型。發電機運行過程中轉子爪極某一時候形變的示意圖如圖1所示。

本文主要考慮圖示旋轉離心力F1和電磁激振力F2的作用，而旋轉離心力F1的作用力方向是確定的，向外偏心，電磁激振力F2為一空間呈正弦分布的激振力，其作用力方向則是交變的。而當兩個作用力方向一致，作用效果正向疊加時，使得爪極形變更為突出，即發電機氣隙磁導模型的變化更為顯著，這將是本文考慮的重點與建模的基本出發點。

圖1 爪極懸臂梁受力及其可能引起的形變

2 爪極形變前后氣隙磁導解析分析計算

由前述推導，參考凸極同步電機中氣隙磁導計算的基本理論，當定轉子的齒正好對齊時，氣隙磁導最大，用直軸磁導Λd表示;當定子齒和轉子槽相對應時，氣隙磁導最小，用交軸磁導 Λq表示［9］，其數學關系式:

式中:θ為距離直軸的電角度值。

應用保角變換，可先依次對氣隙比磁導的各個分值進行求解。應用上述公式，則在汽車發電機中，當轉子爪極與定子齒正好對齊時，氣隙磁導最大，即為直軸磁導Λd;當轉子氣隙部分與定子齒相對應時，氣隙磁導最小，即為交軸磁導Λq。進而可以對汽車發電機主磁路上一個極下的氣隙比磁導進行求解。本文的計算數據均取自最新技術的14 V/1 kW系列汽車用爪極發電機。

(1)當不考慮轉子爪極的形變時，轉子爪極一個極下的直軸比磁導，即其最大比磁導計算式:

式中:β為槽邊假想角，它的數值決定于齒寬對氣隙長度的比值。

將電機沿徑向剖開，其基本結構等效示意圖如圖2所示(圖中已將梯形爪極等效為平行爪極)。

圖2 轉子爪極與定子齒正對齊示意圖

代值計算得 λd=15.96×10－6H/m。

而交軸比磁導，其最小比磁導計算式:

其基本結構等效示意圖如圖3所示。

圖3 轉子氣隙與定子齒正對齊示意圖

代值計算得 λq=1.43×10－6H/m。

參考式(9)，則可計算求得轉子爪極一個極下氣隙比磁導值:

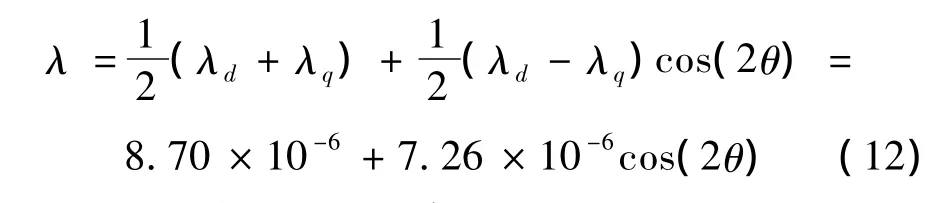
式中:θ為距離直軸的電角度值。

(2)當考慮轉子爪極因受旋轉離心力與同方向的電磁激振力而形變時，如圖1所示，此時爪極面所對應氣隙長度δ(x)沿爪極軸向基本呈非線性函數變化。因此，針對變化氣隙比磁導的解析計算，也可以采用等效的計算方法，即分別求出爪極極尖與極根兩端所對應的氣隙比磁導值，顯然為一最大值λmax與最小值λmin，則此時變化后的氣隙比磁導值即可等效為所求:

假定爪極形變在偏心之后，爪極外表面仍是線性的，其爪極極尖最大偏心距離為0.14 mm。而考慮到發電機原氣隙長度為0.3 mm，因此，爪極偏心之后，爪極極尖所對應的氣隙長度為0.16 mm，此值也即為爪極偏心之后所對應的最小氣隙長度。而爪極極根部位所對應最大氣隙長度仍為0.3 mm。

先對其直軸比磁導進行求解，同式(10)，代入數據，即可求得 λmax=28.60 ×10－6H/m;λmin=15.96×10－6H/m。

變化直軸比磁導值:

變化交軸比磁導值:

同理，參考式(9)，則可計算求得一個極下變化后氣隙比磁導:

式中:θ為距離直軸的電角度值。

3 基于爪極形變的氣隙磁場仿真分析

本文針對汽車發電機氣隙磁導的分析計算中，首先將梯形爪極的發電機轉子等效成平行爪極，然后再應用凸極同步電機的氣隙磁導計算基本理論，分別對發電機在爪極考慮受力形變與不考慮形變的情況下進行氣隙磁導的分析計算。相應的，在汽車發電機的變化氣隙磁導模型的電磁場仿真分析時，也將針對爪極形變與否的兩種情況進行電磁場的建模分析［10］。

應用工程電磁場基本電磁理論，建立汽車發電機的Maxwell 3D模型，對其氣隙磁場進行仿真分析。所建模型的整體模型如圖4所示。

本文的電磁場仿真分析均在發電機額定轉速6 000 r/min時進行，且考慮到如要精確計算旋轉離心力和電磁激振力對爪極形變的影響效果的大小，則將涉及到懸臂梁所受機械應力的分析計算，而這不是本文的研究重點，因此，本文對變化氣隙磁導模型的仿真分析與計算時，將在一個假定的爪極形變值下，也即前面所述的0.14 mm形變下進行。根據爪極形變前后所建兩種模型的鐵心磁密分布云圖如圖5所示。

圖4 汽車發電機仿真計算整體模型

圖5 爪極形變前后仿真磁場云圖

由電機氣隙中沿圓周分布的氣隙磁密除以氣隙合成磁動勢，即可得到相應氣隙比磁導:

在爪極發電機氣隙磁場中，距離其磁場直軸一定電角度的位置各處進行取點，得出氣隙合成磁動勢與氣隙圓周上各點氣隙磁密，然后對每點進行氣隙磁導的數值分析計算，如圖6所示。

圖6 爪極形變前后氣隙磁導基波幅值

相比較而言，基波磁導的值要遠遠大于各階復合諧波磁導，因此在實際計算中通常限于研究基波磁導。這也是本文主要研究對象［11］。

由圖5和圖6可知，爪極形變前后的磁場分布中，發電機定轉子鐵心中的磁場幅值隨著爪極形變后氣隙磁導的增大而相應增加，直接導致了發電機各項電磁性能的改變。針對電機氣隙磁導模型的精確分析計算，主要是為了磁場的分析計算更加精確，由變化的氣隙磁導顯然會導致氣隙磁密空間分布波形的畸變，而氣隙磁場的空間分布波形則是決定電機各項電磁性能的最關鍵因素，對發電機爪極形變前后的氣隙磁場波形的各次諧波仿真分析如圖7所示［12］。

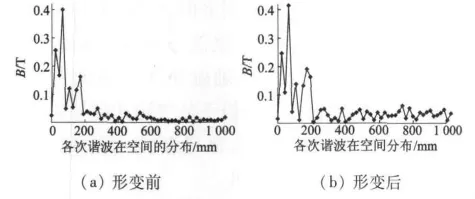
圖7 爪極形變前后氣隙磁場各次諧波分析

根據汽車發電機的調壓原理，當汽車發電系統的輸出電壓UB升高時，發電系統中的調節器會通過減小發電機的勵磁電流If來減小磁通Ф，使發電機的輸出電壓UB保持不變。

又由定子繞組每相感應電勢計算公式:

式中:ω為每相繞組的串聯匝數(即一條支路的匝數);kω1為繞組系數;f為電勢的頻率。

可知，汽車發電機的調壓特性在發電機運行過程中保持感應電勢Eφ1基本不變的同時，也即調節其氣隙磁磁密Bδ值大小基本不變。由上述氣隙磁密各次諧波仿真分析結果可知，當汽車發電機中高速運轉的轉子爪極由于受到旋轉離心力和電磁激振力而產生形變時，氣隙磁密的基波幅值在發電機的調壓過程中下基本保持大小不變時，其它各次諧波及其成分則隨著爪極的形變而顯著增加，如6次諧波增加近20%，這將會給汽車發電機的其它方面的性能，如振動噪聲等方面帶來更大的負面影響。因此，基于氣隙磁導的汽車發電機更為準確的振動噪聲等方面的研究計算，必然需要參考建立本文所述的變化的氣隙磁導模型。

4 計算結果比較分析與結論

本文針對現有的汽車用爪極發電機的氣隙磁導模型進行了分析和計算，并考慮到傳統的思路中氣隙磁導基本不變的局限性，且已經不能滿足高性能爪極發電機的開發，本文采用經典理論與合理等效，提出與建立了汽車用爪極發電機的變化氣隙磁導模型，并針對模型進行了實際電機的分析計算，得出了如下結論:

(1)由前述解析計算與數值計算兩種結果比較分析可知，本文所建模型切實可行，為高性能爪極發電機的設計和優化提供了理論基礎。

(2)在整個電機的運行曲線中，顯然隨著轉速的增加，在不同運行時，轉子爪極所受旋轉離心力大小和電磁激振力的大小與方向都是不停改變的。

(3)由傅里葉分析的氣隙磁密各次諧波比較分析可知，在考慮爪極受力形變時，發電機氣隙磁場畸變嚴重，各次諧波所占比值增大。這也說明了本文所建變化氣隙磁導模型的必要性，特別是在高性能爪極發電機的振動噪聲設計計算時必須加以考慮。

總之，由以上建模與仿真分析可知，汽車用爪極發電機實際運行過程中轉子爪極受力形變必須加以考慮，特別是在高性能汽車發電機的開發與應用中，本文所建的變化氣隙磁導模型將提供設計與優化的理論基礎。

［1］Ibala A，Masmoudi A.Accounting for the armature magnetic reaction and saturation effects in the reluctance model of a new concept of claw － pole alternator［J］.IEEE Transactions on Magnetics，2010，46(11):3955 －3961.

［2］Zarko D，Ban D，Lipo T A.Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent－magnet motor using complex relative air－ gap permeance［J］.IEEE Transactions on Magnetics，2006，42(7):1828 －1837.

［3］Nandi S.A detailed model of induction machines with saturation extendable for fault analysis［J］.IEEE Transactions on Industry Applications，2004，40(5):1302 －1309.

［4］Wang Xiangheng，Chen Songlin，Wang Weijian，et al.A study of armature sinding internal faults for turbogenerators［J］.IEEE Transactions on Industry Applications，2002，38(3):625 －631.

［5］Zarko D，Ban D，Lipo T A.Analytical solution for cogging torque in surface permanent－ magnet motors using conformal mapping［J］.IEEE Transactions on Magnetics，2008，44(1):52 －65.

［6］Boughrara K，Chikouche B L，Ibtiouen R，et al.Analytical model of slotted air－gap surface mounted permanent－magnet synchronous motor with magnet bars magnetized in the shifting Direction［J］.IEEE Transactions on Magnetics，2009，45(2):747 －758.

［7］Zarko D，Ban D，Lipo T A.Analytical Solution for Electromagnetic Torque in Surface Permanent－Magnet Motors Using Conformal Mapping［J］.IEEE Transactions on Magnetics，2009，45(7):2943－2954.

［8］陳曉剛，趙榮祥，黃進，等.凸極同步電機非均勻氣隙磁導的計算［J］.電工技術學報，1998，13(1):15－17.

［9］Bash M L，Pekarek S D.Modeling of salient－ pole wound － rotor synchronous machines for population － based design［J］.IEEE Transactions on Energy Conversion，2011，26(2):381 －392.

［10］畢劉新，王善銘，夏永洪.表貼式永磁電機漏磁導的解析計算［J］.清華大學學報(自然科學版)，2010，50(4):525－528.

［11］Ceban A，Pusca R，Romary R.Study of rotor faults in induction motors using external magnetic field analysis［J］.IEEE Transactions on Industrial Electronics，2012，59(5):2082 －2093.

［12］Wu L J，Zhu Z Q，Staton D A，et al.Comparison of analytical models of cogging torque in surface － mounted PM machines［J］.IEEE Transactions on Industrial Electronics，2012，59(6):2414－2425.