熱聲載荷下薄壁結構非線性振動響應分析及疲勞壽命預測

賀爾銘，劉 峰，胡亞琪，趙志彬

未來飛行器結構工作時將面臨非常嚴苛的載荷環(huán)境，包括機械力載荷、氣動載荷、熱載荷和噪聲載荷等。在熱載荷作用下，薄壁結構將產生很大的面內應力均值;而在熱聲載荷激勵下，薄壁結構響應在多個后屈曲平衡位置之間的跳變會導致非常高的交變應力，因此，熱聲載荷對薄壁結構壽命影響比單一聲載荷要嚴重很多。在熱聲載荷作用下，薄壁結構將以非線性方式振動，這將大大削弱結構壽命。為了保證結構的安全性，就需要確定一種適用于熱聲激勵下評價金屬薄壁結構高周疲勞壽命的方法。

近年來，考慮熱載荷影響的結構聲振疲勞問題一直是航空航天領域的研究熱點，國內外學者在此方面做了大量的基礎性研究工作。沙云東等［1］和金奕山等［2］探討了結構聲疲勞壽命估算的功率譜密度法。Locke等［3-4］首次結合有限元法和模態(tài)疊加法分別計算了梁和平板在熱聲載荷作用下的非線性隨機響應問題。Spottswood等［5］采用降階法在保證求解精度的情況下大大縮短了計算時間。Dowling［6］基于不同合金材料的疲勞實驗數(shù)據研究了多種應力壽命模型，并給出了多種材料在常見應力壽命模型中的相關參數(shù)。Przekop等［7］研究了跳變響應對金屬薄壁結構熱聲疲勞壽命的影響，文中指出屈曲后的薄板梁存在兩個振動平衡位置，而結構在兩個平衡位置之間的跳變所產生的交變應力是導致熱屈曲后結構熱聲疲勞壽命降低的主要因素。以上文獻都明確了研究金屬薄壁結構熱聲疲勞特性問題的重大意義，但迄今為止國內外學者的研究工作大都集中于評價熱聲激勵下薄壁結構響應特性分析，很少有文獻系統(tǒng)地評價金屬薄壁結構的熱聲疲勞特性，亦未見分別評價熱載荷及噪聲載荷對薄壁結構熱聲疲勞壽命特性影響機理的研究。

本文建立了典型薄板梁模型，仿真分析了其在不同熱聲載荷工況下的非線性響應特性，得出了不同熱載荷工況下薄板梁的熱模態(tài)振型變化規(guī)律，在此基礎上，分別采用四種應力壽命模型基于Miner線性理論預測了薄板梁的熱聲疲勞壽命，并對不同應力壽命模型的熱聲疲勞預測結果進行了評價。

1 熱聲載荷下薄板梁的振動方程

薄板梁在熱聲載荷下非線性振動的動態(tài)離散有限元方程可表示為［5］:

式中:M為質量矩陣，C為阻尼矩陣，KL、K1、K2分別為線性、二次、三次剛度矩陣，X是位移列陣，F(xiàn)是聲載荷列陣。熱載荷的影響體現(xiàn)在式(1)的兩端，F(xiàn)ΔT表示由線性剛度矩陣 KΔT(ΔT)改變而引起的熱應力載荷列陣。

為了便于計算，式(1)還可以表示為:

式中:FNL表示考慮了熱載荷影響的含有線性、二次及三次剛度項的恢復力。采用Newmark-Beta積分法計算機仿真即可得到薄板梁在熱聲載荷下的動態(tài)響應。

2 熱聲載荷下薄板梁振動的非線性響應特性

選取航空航天領域內廣泛采用的鈦鋁合金(2024-T3)薄板梁為研究對象，建立其有限元模型如圖1，其幾何尺寸為:460 mm×25.4 mm×2.29 mm。材料參數(shù)為:楊氏模量E=73 GPa，密度 ρ=2 768 kg/m3，泊松比μ =0.32，熱膨脹系數(shù) α =22.3 ×10-6/℃。

圖1 薄板梁有限元模型Fig.1 Finite element model of the beam

薄板梁模型由144個殼單元組成，其約束條件為:AD邊和BC邊固支，AB邊和CD邊自由。

2.1 噪聲載荷下薄板梁非線性響應分析

聲載荷處理為聲壓級SPL幅值服從高斯分布的均勻白噪聲，帶寬Δf為0～1 500 Hz，其功率譜密度為:

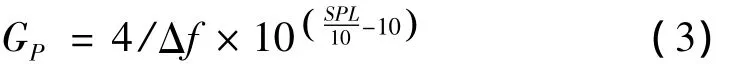
對薄板梁進行模態(tài)分析，可得其前四階固有頻率依次為57.8 Hz，159 Hz，312 Hz，516 Hz。采用時域分析法分別將140 dB，155 dB，160 dB的隨機噪聲以面力的形式均勻地施加在模型的所有殼單元上，為防止載荷沖擊的影響，故將0～0.2 s的響應結果剔除，仿真得出0.2～2 s內薄板梁在三種強度噪聲下的響應特性如圖2～3。

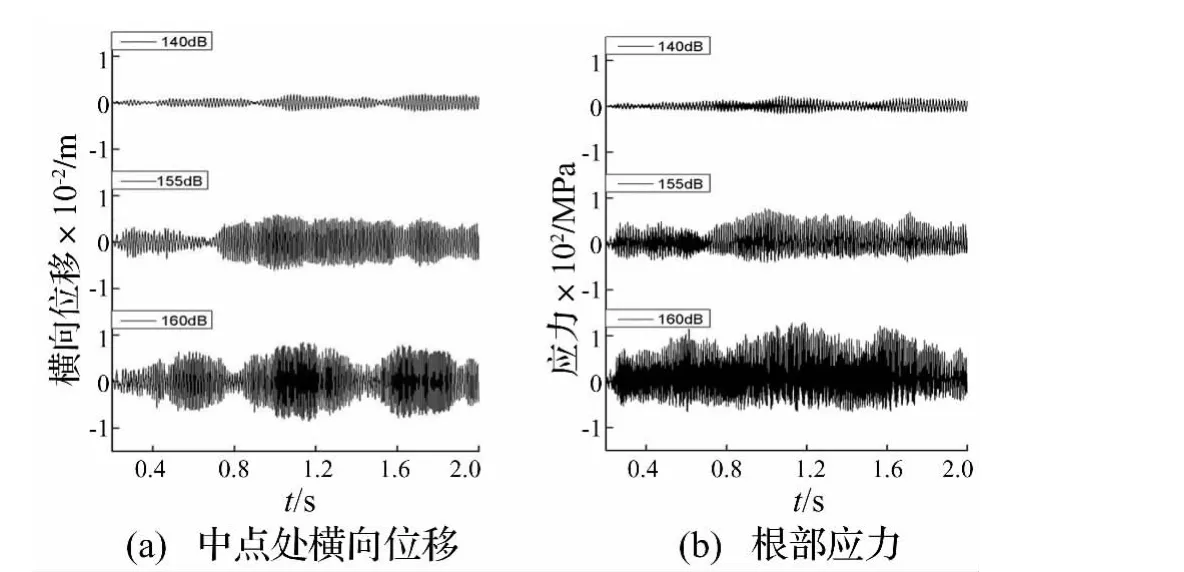
圖2 屈曲前(ΔT=0℃)薄板梁中點處橫向位移和根部應力時間歷程Fig.2 Center transverse displacement response andclamped end stress response，ΔT=0℃

載荷均值和載荷幅值是預測結構壽命過程中的兩個重要參數(shù)，由圖2(a)得，在不同強度噪聲載荷下，屈曲前的薄板梁僅繞著橫向位移為零的初始位置振動，此時薄板梁中點處振動位移和根部應力的均值均為零。薄板梁中點處位移及根部應力的幅值均方根(RMS)見表1。

從表1得知，薄板梁中點處位移及根部應力均隨噪聲增強而增大，當聲壓級從140 dB增至155 dB時，中點處位移幅值增加了2.71倍，根部應力幅值增加了2.26倍;而當聲壓級再增至160 dB時，中點處位移幅值增加了0.3倍，根部應力幅值增加了0.8倍。由圖3(a)可見，薄板梁在不同聲壓級下的位移響應峰值的極大值均出現(xiàn)在薄板梁基頻處，且位移響應峰值處的振動能量隨噪聲增強而增大;從圖3(b)可見，薄板梁的前兩階模態(tài)頻率在聲激勵響應中起主導作用，且根部應力響應峰值對應的振動能量也隨噪聲增強而增大;從圖3(a)、(b)還可看出，不同聲壓級下薄板梁中點處位移和根部應力響應峰值隨噪聲增強而右移，這是由于噪聲作用下結構幾何非線性改變了薄板梁剛度而引起的。

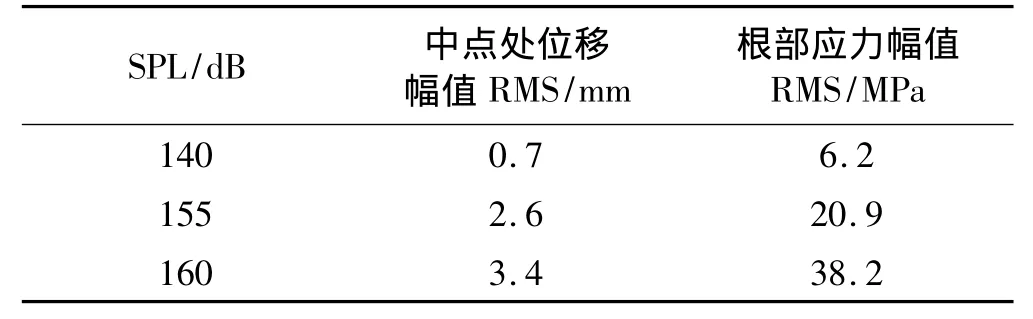
表1 屈曲前(ΔT=0℃)薄板梁中點處振動位移及根部應力RMSTab.1 Center displacement response and clamped end stress response RMS，ΔT=0℃

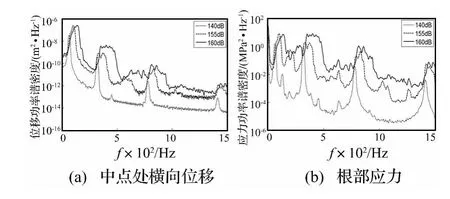
圖3 屈曲前(ΔT=0℃)薄板梁中點處橫向位移和根部應力功率譜密度Fig.3 Center transverse displacement response and clamped end stress response PSD，ΔT=0℃

2.2 熱聲載荷下薄板梁響應特性分析

2.2.1 薄板梁熱模態(tài)分析

屈曲前后薄板梁的剛度變化趨勢相反，因此薄板梁的模態(tài)振型也將會有很大變化。由熱屈曲分析可知薄板梁的臨界屈曲溫度Tcr=3.76℃。溫度梯度對薄板梁響應的影響很小，故本文考慮無溫度梯度的均勻溫度場。設置一個屈曲前工況ΔT=0℃，考慮了三個屈曲后工況:ΔT=10℃、20℃及40℃，以便于與ΔT=0℃工況進行對比分析。圖4為薄板梁在這四種溫度場中的前四階模態(tài)頻率及振型。

薄板梁的模態(tài)頻率和振型隨溫度的升高而變得比較復雜。屈曲前，熱膨脹受到約束的薄板梁產生的面內應力將降低結構剛度，從而降低模態(tài)頻率;當溫度達到臨界屈曲溫度時，薄板梁剛度降至最低，此時梁處于承載能力最弱的失穩(wěn)狀態(tài)，各階模態(tài)頻率取得最小值;隨著溫度繼續(xù)升高，由于熱硬化效應的影響，梁結構將出現(xiàn)永久屈曲變形，不同階次的頻率增長趨勢有很大不同，前三階模態(tài)頻率呈上升趨勢，而第四階模態(tài)頻率降低，總體呈集中趨勢，因此在屈曲后狀態(tài)下，可能發(fā)生不同階次模態(tài)頻率的耦合共振，即發(fā)生非線性跳變響應。

圖4 薄板梁在不同溫度下前四階模態(tài)頻率和振型Fig.4 The first four mode shapes for the beam，as a function of temperature

2.2.2 熱載荷對薄板梁噪聲響應特性的影響

為了研究屈曲后跳變響應對薄板梁熱聲疲勞壽命影響的嚴重程度，以ΔT=20℃工況下的薄板梁為例，研究了薄板梁分別在140 dB、155 dB、160 dB的隨機噪聲激勵下0.2～2 s內的響應規(guī)律，如圖5所示。表2為在此工況下薄板梁中點處位移和根部應力響應的統(tǒng)計結果。

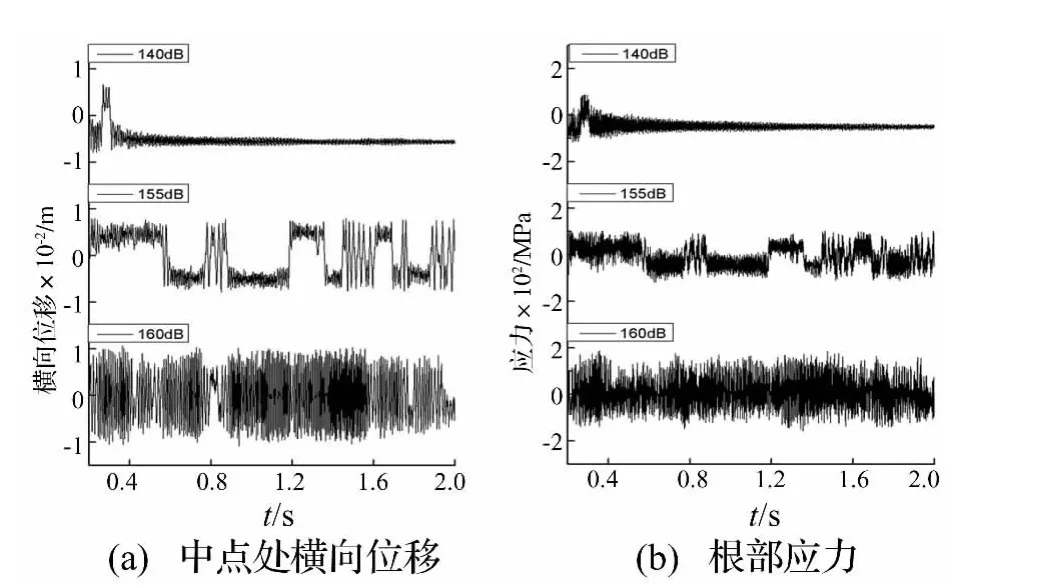
圖5 屈曲后(ΔT=20℃)薄板梁中點處橫向位移和根部應力時間歷程Fig.5 Center transverse displacement response and clamped end stress response，ΔT=20℃

表2 屈曲后(ΔT=20℃)薄板梁中點處位移及根部應力響應Tab.2 Center displacement response and clamped end stress response RMS，ΔT=20 ℃

熱屈曲后的薄板梁存在兩個穩(wěn)定的振動平衡位置。從圖5(a)可看出，140 dB噪聲作用下薄板梁僅圍繞一個橫向位移不為零的平衡位置振動，結合表2中140 dB工況的響應結果可知，薄板梁中點在此平衡位置處的橫向振動位移均值為 -5.2 mm，幅值為1.5 mm;當聲壓級增至155 dB時，薄板梁將圍繞著兩個振動平衡位置發(fā)生間歇性跳變響應，表2中的155 dB工況分別給出了這兩個平衡位置應力和位移的均值及幅值。進一步分析可知，在各自平衡位置處發(fā)生間歇性跳變時，薄板梁中點處位移和根部處應力幅值及均值均并未發(fā)生較大改變，此時，熱聲疲勞壽命的削弱量由薄板梁響應的跳變頻率決定;而當聲壓級增至160 dB時，薄板梁僅圍繞一個橫向位移為-0.1 mm的平衡位置發(fā)生持續(xù)性跳變響應，顯著增加的跳變頻率使薄板梁中點處位移幅值增加了2.2倍，根部應力幅值增加了1.7倍，因此薄板梁的熱聲疲勞壽命將被大大削弱。

將薄板梁在不同工況下的熱聲振動響應情況劃分為三類:未發(fā)生跳變(N)、間歇性跳變(I)及持續(xù)性跳變(P)，如表3所示。

表3 薄板梁在不同熱聲載荷作用下的響應情況Tab.3 Response matrix characteristics under thermal-acoustic loading

從圖6(a)可見，薄板梁熱屈曲后(ΔT=20℃)中點處的橫向位移響應隨噪聲增強而呈增大趨勢，不同聲壓級噪聲激勵下薄板梁的位移響應峰值變化趨于復雜，位移功率譜密度曲線規(guī)律雖然不再統(tǒng)一，但其基頻模態(tài)在熱聲響應中仍然起主導作用。從圖6(b)可見，薄板梁的應力響應具有明顯的多模態(tài)特征，根部應力響應也隨噪聲增強而呈增大趨勢，但未反映出明顯的優(yōu)勢頻率，中低頻段是薄壁結構熱聲響應研究的重點頻段。

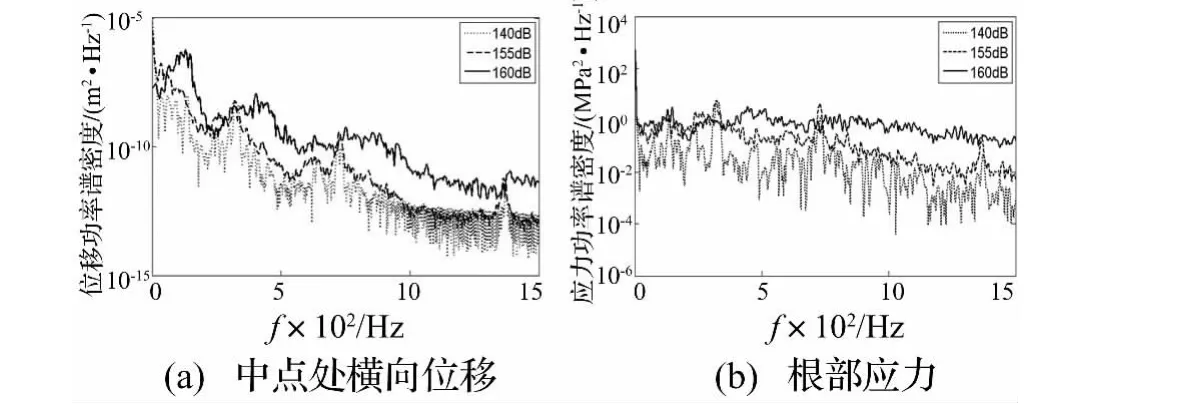
圖6 屈曲后(ΔT=20℃)薄板梁中點處橫向位移和根部應力功率譜密度Fig.6 Center transverse displacement response and clamped end stress response PSD，ΔT=20 ℃

3 薄板梁熱聲疲勞壽命估算

3.1 編制載荷譜

載荷譜直接關系到結構損傷度的計算，因此需要對觀測的載荷譜進行統(tǒng)計，以便得到不同大小應力幅的出現(xiàn)概率。常用的波形計數(shù)法有峰值計數(shù)法、變程計數(shù)法和雨流計數(shù)法，各種方法具有各自的特點及其適用范圍。峰值計數(shù)法需要統(tǒng)計載荷波形中落在各載荷等級中的所有峰值數(shù)，這種方法記錄了載荷波動信息，但夸大了實際載荷中小載荷波動的幅值，使壽命估計結果偏于保守。變程計數(shù)法只考慮載荷幅值而忽略了載荷均值對結構壽命的影響。雨流計數(shù)法是一種綜合考慮結構動強度(載荷幅值)和靜強度(載荷均值)的計數(shù)法，能比較全面地反映載荷的真實情況，目前在結構疲勞壽命估算中應用最為廣泛［7-8］。本文運用雨流計數(shù)法統(tǒng)計了薄板梁在ΔT=20℃工況下，根部最大應力點在0.2～2 s內的熱聲應力響應結果如圖7所示，然后將各個載荷循環(huán)用于損傷度計算。

圖7 屈曲后(ΔT=20℃)薄板梁根部應力幅值—均值直方圖Fig.7 3-D stress rainflow ranges histogram at the clamped end

3.2 隨機疲勞壽命分析模型

某應力水平下的損傷度一般要通過材料的S-N曲線來估算。進行壽命預測時往往很難找到恰好適用的S-N曲線，所以需要依據經驗，按照恰當?shù)膲勖Ｐ蛯嶒烖c擬合而得出。Dowling［6］研究了適用于鋁合金(2024-T3)的多種應力壽命模型。比較經典的有Goodman模型和Morrow模型，均可由下式表示:

Walker模型應用也比較廣泛，其假定失效所經歷的循環(huán)次數(shù)為:

式中:Aw=σf'w2bw，σf'w=1 772 MPa，bw= -0.163 和 γ =0.460。當循環(huán)比R＜-2時，Walker模型將會產生較大誤差［6］。美國交通運輸部標準［9］給出的 W alker模型修正公式為:

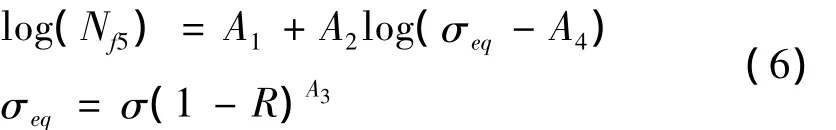
式中:A1=11.1，A2=-3.97，A3=0.56，A4=15.8。

3.3 線性累積損傷理論

Miner模型是工程上廣泛采用的一種線性累積損傷模型。如果是單級加載，循環(huán)比等于1時即出現(xiàn)破壞。如果是多級加載，總損傷等于各循環(huán)比(或損傷比)的總和，且當循環(huán)比總和等于1時發(fā)生破壞。在多個應力水平作用下的損傷度計算公式為:

應用線性累積損傷理論來計算疲勞壽命時，主要是將載荷譜中各級載荷循環(huán)作用的順序和次數(shù)用雨流計數(shù)法篩選出來，而各級載荷之間的遲滯效應則不予考慮。

3.4 薄板梁熱聲疲勞壽命預測及結果分析

基于上述四種應力壽命模型，預測出的鈦鋁合金(2024-T3)薄板梁不同工況下的熱聲疲勞壽命如表4。

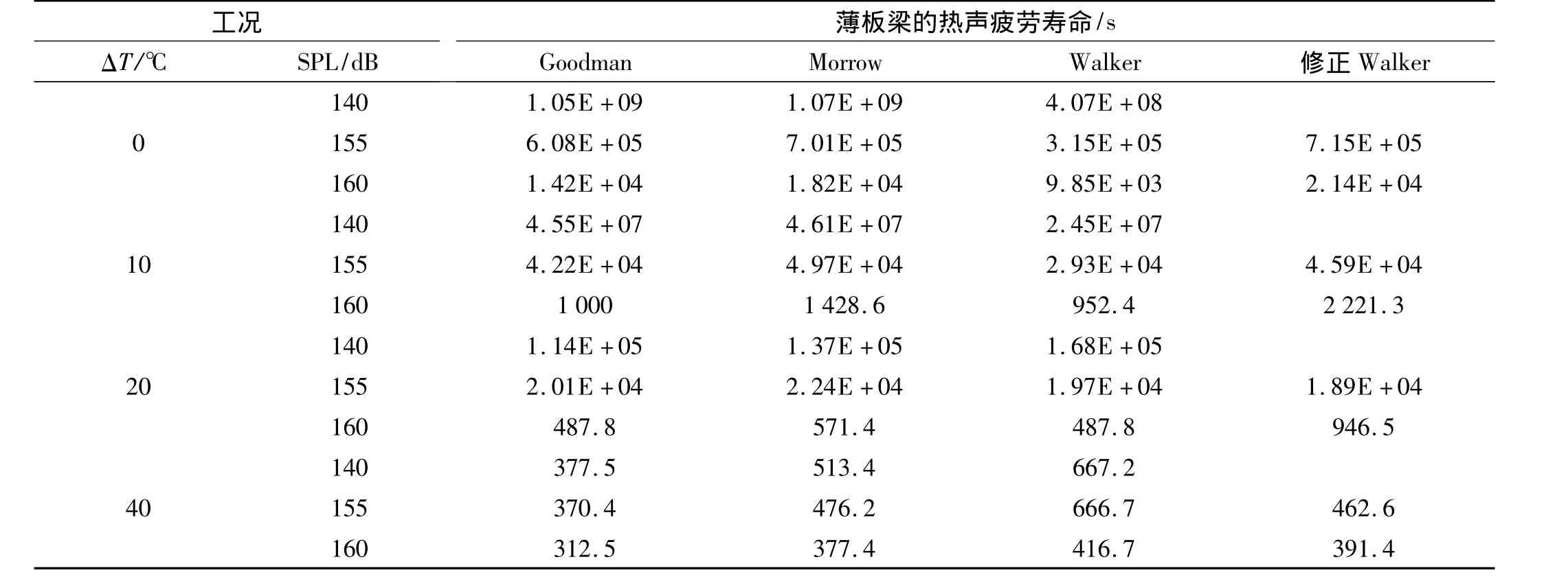
表4 不同工況下薄板梁根部的熱聲疲勞壽命Tab.4 Clamped end fatigue estimates of the beam subject to thermal-acoustic loading

分析表4可知，ΔT=0℃、10℃工況下，基于Walker模型的熱聲疲勞壽命預測結果最保守，此時基于Goodman和Morrow模型預測薄板梁壽命更可靠;ΔT=20℃工況下，基于修正Walker模型的預測結果與其它三種模型相比偏差較大，此時基于Goodman、Morrow和Walker模型的預測結果更可信;ΔT=40℃工況下，基于Goodman模型的預測結果最保守，但由于采用四種模型的預測結果偏差不大，因此可認為此時基于四種模型的薄板梁熱聲疲勞壽命的預測結果均是準確的。

在ΔT=0℃的屈曲前工況下，噪聲聲壓級由140 dB增至155 dB時，薄板梁的壽命將減小3個量級;當噪聲達到160 dB時，幾何非線性影響進一步增強致使薄板梁的壽命再減小1.5個量級;在屈曲后的三個工況(ΔT=10℃、20℃、40℃)中，隨著噪聲的增強薄板梁的熱聲疲勞壽命雖不斷減小，但其減小幅度有所降低，這是因為熱載荷增大了薄板梁的剛度，應力響應幅值隨噪聲增強而增大幅度減小所致;薄板梁處于ΔT=40℃工況時，熱聲疲勞壽命減小量很小，此時影響結構熱聲疲勞壽命的主要因素是熱載荷;再比較表4中同種強度噪聲下不同熱載荷工況薄壁梁壽命結果可知，噪聲是影響屈曲前薄板梁熱聲疲勞壽命的主要因素，而熱載荷是影響屈曲后薄板梁熱聲疲勞壽命的主要因素。

高速飛行器蒙皮、發(fā)動機結構或是發(fā)動機的尾噴管附近的溫度均是非常高的，常常比本文算例中的溫度要高出很多，結構熱聲疲勞壽命損失將會更嚴重，因此研究熱聲載荷聯(lián)合作用對薄壁結構熱聲疲勞壽命的影響具有非常重大的意義。

4 結論

本文基于時域分析法分別研究了薄板梁在聲載荷和熱聲載荷下的非線性振動響應特性，并預測了薄板梁的疲勞壽命。通過本文研究可得出以下重要結論:

(1)薄板梁在不同溫度下的剛度會發(fā)生較大變化，從而導致其在不同溫度下熱聲響應的基頻發(fā)生較大變化，在結構抗疲勞設計時需要分析薄壁結構工況溫度下的熱模態(tài)，避開熱模態(tài)基頻。

(2)在聲壓級足夠大的噪聲載荷下，熱屈曲后的薄板梁會發(fā)生非線性跳變響應，導致薄板梁應力幅值急劇增加，從而嚴重削弱薄板梁的熱聲疲勞壽命。

(3)噪聲載荷是影響屈曲前薄板梁熱聲疲勞壽命的主要因素，而熱載荷是影響屈曲后薄板梁熱聲疲勞壽命的主要因素。

(4)在ΔT=0℃、10℃工況下，基于Goodman和Morrow模型的鈦鋁合金(2024-T3)薄板梁壽命預測結果更可靠;在ΔT=20℃工況下，基于Goodman、Morrow和Walker模型的預測結果更可信;在ΔT=40℃工況下，基于Goodman模型的預測結果最保守。

本文基于時域分析法的薄壁結構熱聲疲勞壽命預測方法可直接應用于金屬薄壁結構熱聲疲勞壽命預測問題中，也可為金屬薄壁結構的抗熱聲疲勞設計提供一定參考。

［1］沙云東，郭小鵬.隨機聲載荷作用下的復雜薄壁結構Von Mises應力概率分布研究［J］.振動與沖擊，2011，30(1):137-141.SHA Yun-dong，GUO Xiao-peng.Probability distribution of Von Mises stress for complex thin-walled structures undergoing random acoustic loadings［J］.Journal of Vibration and Shock，2011，30(1):137-141.

［2］金奕山，李 琳.關于航空發(fā)動機結構聲疲勞壽命估算方法的探討［J］.航空動力學報，2003，6(3):374-377.JIN Yi-shan，LI Lin.Sonic fatigue life prediction of aeroengine structure［J］.Journal of Aerospace Power，2003，6(3):374-377.

［3］ Locke J E.A finite element formulation for the large deflection random response of thermally buckled structures［D］.Ph.D.Dissertation，Old Dominion University，Norfolk，VA，1988.

［4］Locke J E，Mei C.A finite element formulation for the large deflection random response of thermally buckled beams［J］.A1AA Journal，1990，28:2125-2131.

［5］ Spottswood S M，Joseph J H.Reduced-order models for a shallow curved beam under combined loading［C］.AIAA Journal，48(1)，January 2010.

［6］ Dowling N E.Mean stress effects in stress-life and strain-life fatigue［C］.Fatigue 2004:Second SAE Brasil Conference on Fatigue，SAE 2004-01-2227，S?o Paulo，Brasil，2004.

［7］ Przekop，Adam，Stephen A，et al.An Investigation of Highcycle fatigue models for metallic structures exhibiting snapthrough response［C］.48th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference，Honolulu，Hawaii，April 23-26，2007，AIAA 2007-2204.

［8］ Khosrovanch A K，Dowling N E.Fatigue loading history reconstruction based on the rain-flow technique［J］.International Journal of Fatigue，1990，12(2):99-106.

［9］ Metallic Materials PropertiesDevelopment and Standardization(MMPDS-01)［S］.U.S.Department of Transportation，Knovel Interactive Edition，2004.