一種求非線性振動系統周期解的切比雪夫級數方法

周 薇，韓景龍，陳全龍

近十幾年，國內外學者在求非線性振動系統周期解方面進行了大量研究，不僅改進了傳統算法［1－5］，而且還提出了一些新方法［6－11］。周期解的穩定性問題是非線性動力學中又一重要研究內容，通常用Floquet理論研究［12］。目前，針對非線性振動系統求解方法的研究雖然已經取得了重大進展，但仍面臨不斷改進方法適用范圍、提高求解精度以及降低計算復雜度等方面的問題［13］;已有計算近似Floquet轉移矩陣(FTM)的數值方法也普遍存在精度較低的局限［6］。

切比雪夫多項式是數值逼近領域中一類重要的基函數，它不但具有一致收斂性［14］，而且在精確逼近函數的同時能有效降低高階差值的Runge現象［15］。雖然利用切比雪夫多項式求解常微分方程的研究起步較早［16］，但在最近十幾年它才被應用于非線性周期系數微分系統的各項研究［10，17－24］。

鑒于利用15～18項移位的第一類切比雪夫級數可以非常精確地逼近三角函數［25］和高維系統的FTM(如20×20維)［24］，本文將移位的第一類切比雪夫級數理論和非線性優化算法結合，提出了一種求非線性振動系統周期解的方法。本方法將狀態矢量中未知切比雪夫系數的求解，轉化為對主周期上系統殘差求最小值的無約束最優化問題，計算出了具有較高精度的切比雪夫級數周期解。以Duffing系統和直升機旋翼運動系統為例，通過與諧波平衡法(HBM)比較，驗證了本方法正確有效，算例同時表明，將切比雪夫級數理論引入到直升機氣彈響應與穩定性分析領域正確、可行。

1 切比雪夫級數周期解及其穩定性分析

考察非線性振動系統:

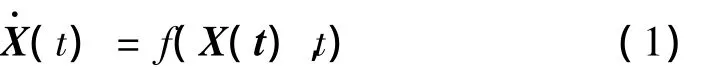
其中:X(t)={x1(t)，x2(t)，…xn(t)}T是 n×1維列向量，f(X(t)，t)是周期為T的函數。

在非線性動力學中，與平衡點的確定相比，確定周期運動的存在性和數目是更加困難的問題。通常僅求解所關心的一部分周期運動。設系統(1)的周期解為:

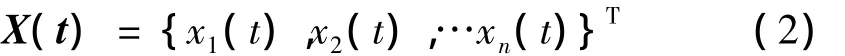
將其解展開為m項移位的第一類切比雪夫級數，具有如下形式

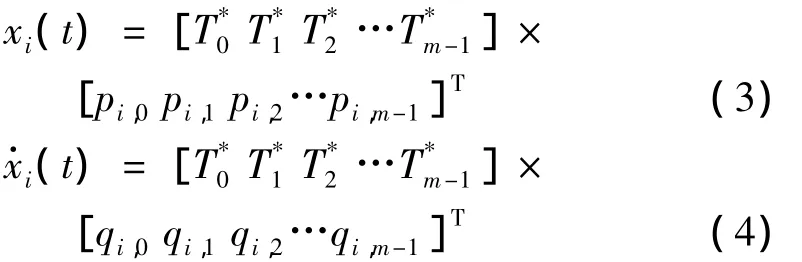
為了在今后使用局部優化方法時能夠合理估計優化初值，同時將周期解(2)展開為N階諧波級數:

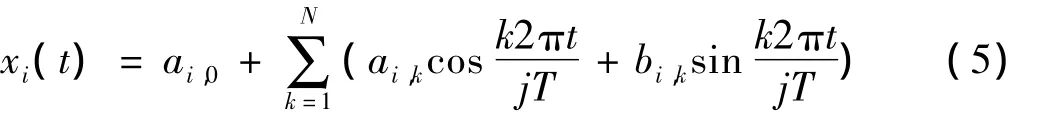
其中:ai，k和 bi，k是周期解中(2N+1)·n 個未知系數，i=1，2，…，n。對于單周期軌道，取j=1;對于倍周期軌道，取j=2n，n為周期倍化分岔的次數。以單周期軌道為例，此時(3)～(5)滿足如下關系:

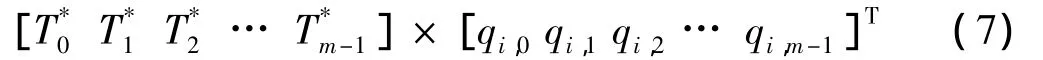
因為移位的第一類切比雪夫多項式的定義區間為［0，1］，所以必須對系統進行周期歸一化，即做變換t=T×s且s∈［0，1］。在實際計算時，只需將系統方程展開為切比雪夫級數，并將所有ω代換為2π，t代換為s，取為關于s的多項式即可。將式(1)右端移項后，求得系統殘差R(s)，用符號表示如下:

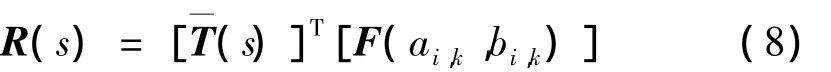
其中:［F(ai，k，bi，k)］是由系統方程決定的 n m × 1 維未知列向量，且每個行分量是關于 ai，k和 bi，k的多項式。(s)］T，?代表Kronecker乘法，I為單位矩陣。對精確解而言，在一個周期上任意時刻s0∈［0，1］，均有殘差R(s0)=0。設Ri(s)為殘差R(s)每一行分量，則所設周期解與精確解誤差越小，等價于在周期［0，1］上任意時間點處Ri(s)的絕對值越小，表達成非線性最優化問題為:

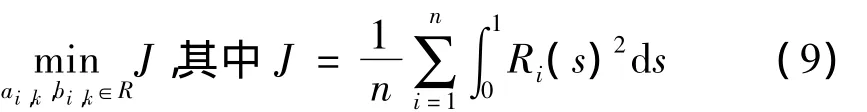
利用優化算法可以求得未知系數 ai，k和 bi，k，由式(6)求得pi，j即為周期解的切比雪夫系數。

不妨采用局部優化方法中的擬牛頓法［26］來求解式(9)。由于初值選取對優化結果有影響，通過調整式(6)中諧波展開項數(也可直接參照諧波平衡法選取諧波項數)，使優化初值處于合理范圍，從而避免盲目試值。若能夠利用其它方法合理估計優化初值，則可以不用式(6)和(7)中的諧波展開，直接求解切比雪夫系數pi，j。特別地，一些工程問題的周期解(如算例2.2.1)雖然能夠估計出一個合理的可行域閉區間，從而利用確定性方法求全局最優解，但卻會大大增加時間復雜度和計算復雜度，有時并不必要。

下面分析周期解的穩定性。設X0(t)是已求得的切比雪夫級數解，ΔX(t)為小擾動，令

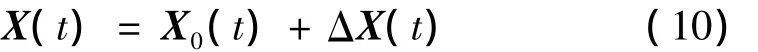
把式(10)代入原系統方程，略去高階小量，最后得到以Δx(t)為未知量的線化方程

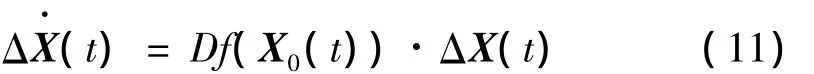
由線性周期系統理論和切比雪夫級數運算性質，只需將單位矩陣的每一列分別作為初始條件，通過積分求得一個周期末點ΔX(T)的值，即為FTM相應列的向量［25］。根據Floquet理論，若FTM特征值的模均小于1，則周期解漸近穩定性;否則不穩定。

計算系統殘差、目標函數和FTM時需用到移位的第一類切比雪夫多項式及其乘法、積分算子矩陣，詳見文獻［10，25］。本文在計算時均取前18項移位的第一類切比雪夫多項式。

2 算例分析

2.1 Duffing系統

以具有立方非線性的Duffing系統方程為例

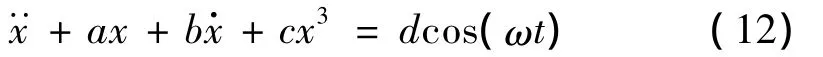
其中:a=5，b=2，c=18，d=8，ω =2。

在求切比雪夫級數周期解時，先對變量t做變換t=2πs/ω (s∈［0，1］)，將時間周期歸一化，再計算系統殘差R。當取3階諧波時，利用諧波平衡法和優化方法分別求得系統周期解中的未知系數如表1所示。

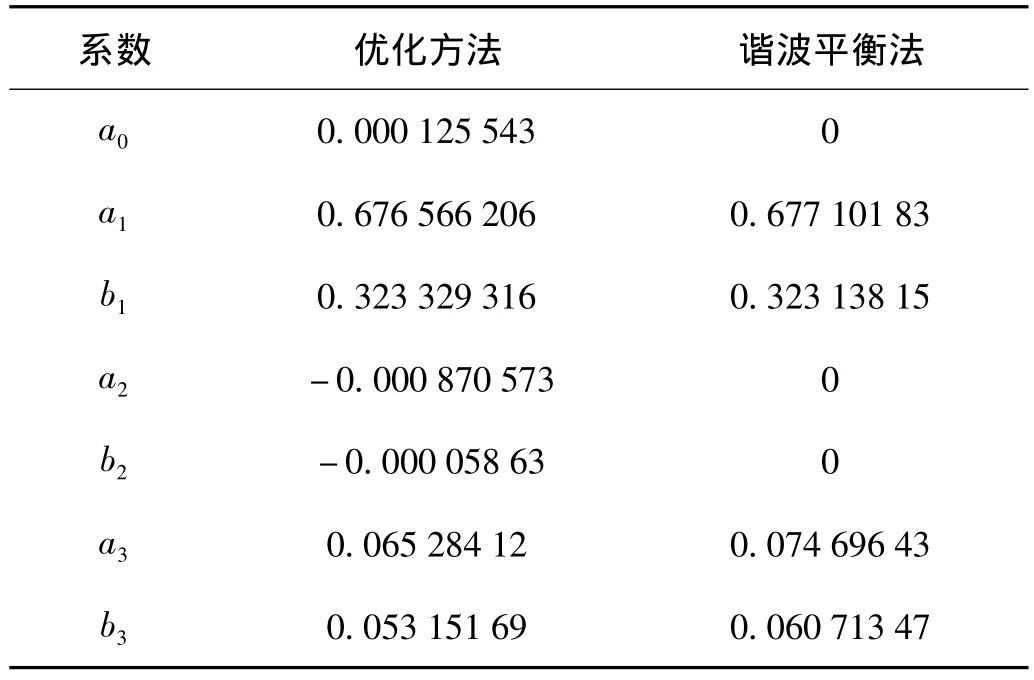
表1 Duffing系統周期解系數Tab.1 Periodic solution coefficients of Duffing system

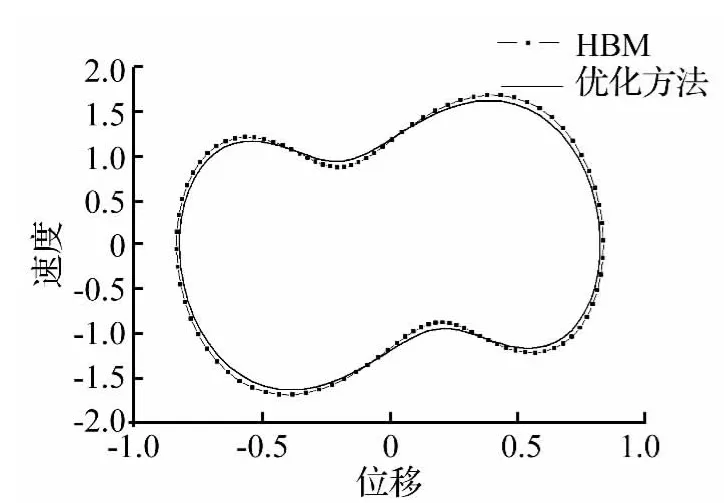
圖1 Duffing系統相圖(取3階諧波)Fig.1 Phase diagram of Duffing system(take 3－order harmonics)

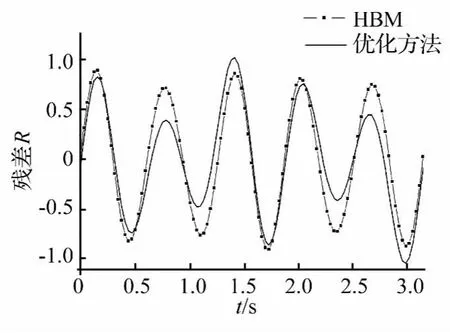
圖2 殘差曲線(取3階諧波)Fig.2 Residual curves(take 3－order harmonics)

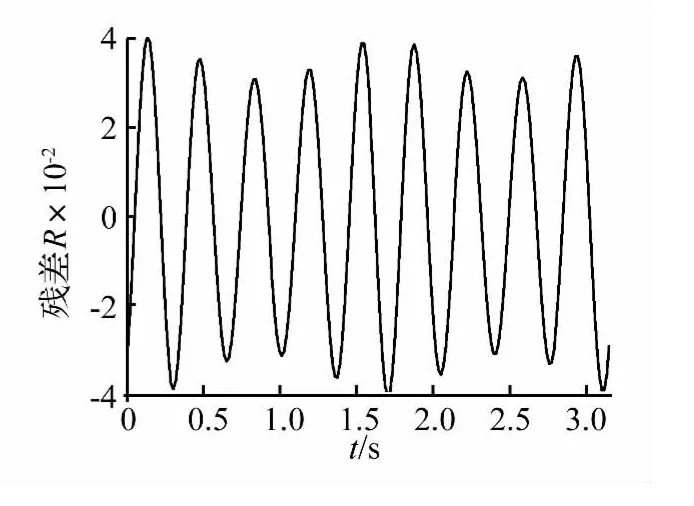
圖3 諧波平衡法殘差曲線Fig.3 Residual curve of HBM

圖1 中給出了同取3階諧波時，優化方法和諧波平衡法所得到的系統相軌跡圖，二者吻合良好。將系統代入諧波平衡法求得的周期解后，系統絕對殘差的均值為0.516;而代入切比雪夫級數周期解，系統絕對殘差的均值為0.454，精度提高13.6%。圖2為此時系統在一個周期上的殘差曲線。同取6階諧波展開時，利用諧波平衡法所得系統絕對殘差的均值為0.022，而優化方法所得系統絕對殘差的均值為1.22×10－5。二者在一個周期上的殘差曲線分別如圖3、圖4所示。可見，通過調整諧波展開項數來改變優化算法初值可以降低殘差量級，有效保證求解精度。

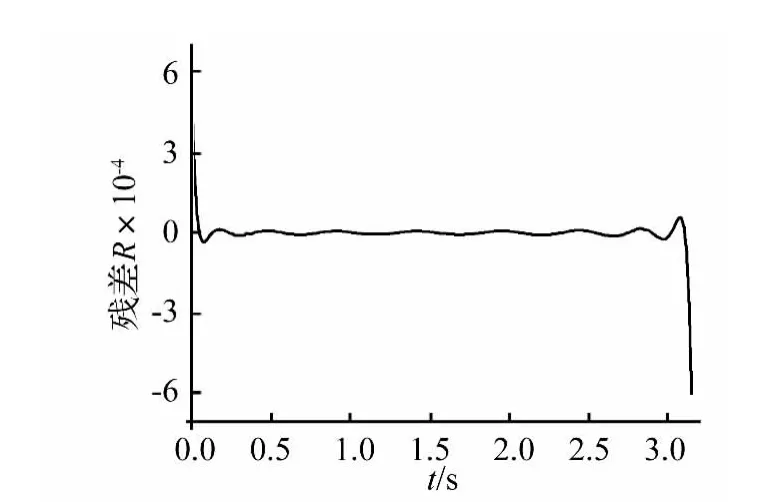
圖4 優化方法殘差曲線Fig.4 Residual curve of optimization method

下面進行穩定性分析。由線性周期系統理論和切比雪夫級數運算性質，經過計算，存在一個Floquet乘子的模為27.271，周期解不穩定。

2.2 直升機旋翼系統

旋翼響應與穩定性問題，是直升機動力學中一個重要研究課題。旋翼動力學模型是包含了結構、慣性和氣動載荷非線性的時變常微分方程組。通常采用諧波平衡法、時間有限元法等求解。

2.2.1 鉸接式旋翼系統

以3片槳葉的鉸接式直升機旋翼系統運動為例，考慮旋轉平面內如圖5、圖6所示的揮舞、擺振運動。假設旋翼每片槳葉性質相同，建立單片槳葉揮舞、擺振耦合運動方程:

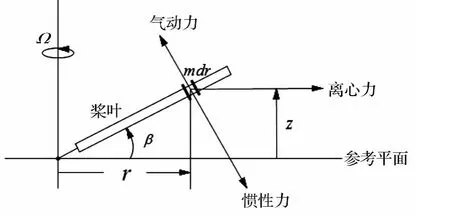
圖5 揮舞運動受力示意圖Fig.5 Force diagram of flapping motion

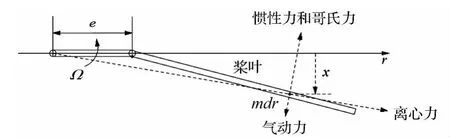
圖6 擺振運動受力示意圖Fig.6 Force diagram of lagging motion

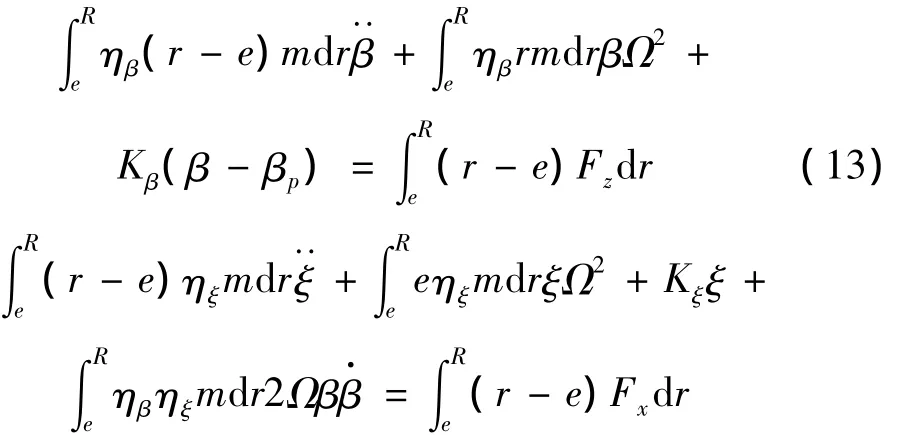
其中:Fx、Fz分別為平行和垂直于槳盤平面的剖面氣動力，其詳細表達式以及式中符號含義參見文獻［27］。計算中用到的旋翼參數如表2所示。

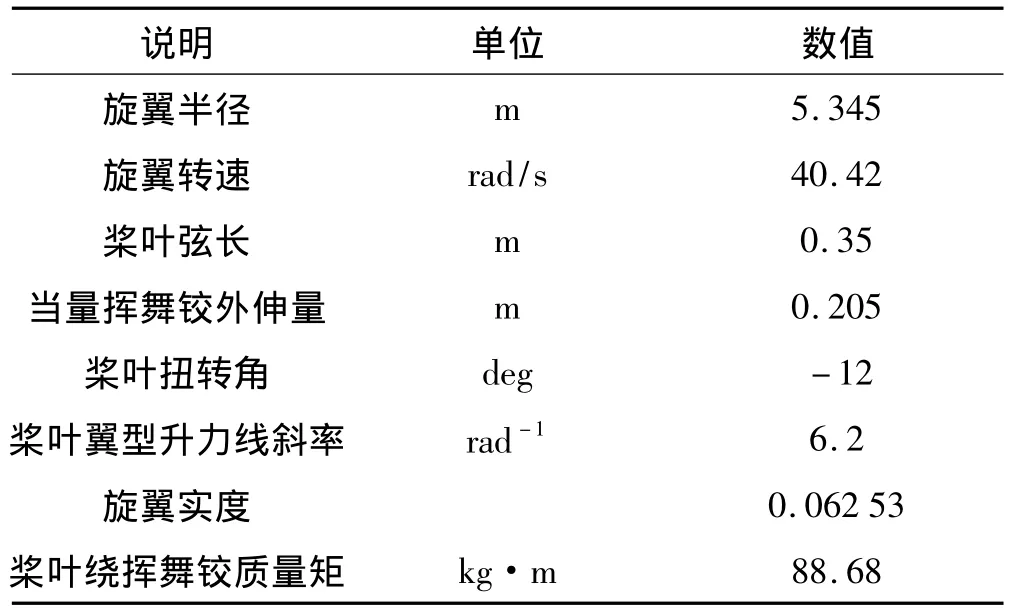
表2 主要參數Tab.2 Main parameter

當前進比為0.2時，采用前飛條件下的Dress入流模型，總距 θ0=0.116 rad，周期變距 θC=0.035 rad，θS=－0.064 rad。將無量綱化后的參數代入系統方程，再進行周期歸一化，最后得到各方程的殘差Ri。在展開為2階諧波時，諧波平衡法所得揮舞、擺振運動方程絕對殘差的均值分別為1.24和0.241，由于略去諧波的量級較大，產生了錯誤結果。而代入優化方法所得周期解，系統絕對殘差的均值分別為0.53和0.227，結果較準確。這是由于本方法所取諧波僅用于修正優化初值，而周期解仍由18項移位的第一類切比雪夫級數逼近。圖7，圖8顯示了取3階諧波時，兩種方法所得槳葉運動的殘差曲線，本方法精度提高5.2%。在同展開為7階諧波時，諧波平衡法和優化方法所得的系統絕對殘差的均值均達到10－6量級，具有較高精度，此時系統相圖如圖9，圖10所示。

最后分析周期解的穩定性。用切比雪夫級數的積分運算來求得 FTM，Floquet乘子的模分別為0.096 3和0.680 2。此直升機旋翼系統在前進比為0.2時的揮舞、擺振周期運動均漸近穩定。

2.2.2 無鉸式旋翼系統

在旋轉坐標系下，以有限元法［28］建立槳葉運動方程，如圖11所示。

所得槳葉方程用符號表示為［28］:

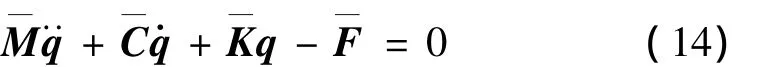
其中:q(t)是單片槳葉上總節點位移向量，q(t)={u1，v1，v1'，w1，w1'，φ1，…u14，φ10，u15}，u、v、w、φ 分別為槳葉彈性軸上各節點拉伸、擺振、揮舞、扭轉自由度的彈性位移。算例采用文獻［28］中BO105旋翼參數、準定常氣動力和Drees入流模型。

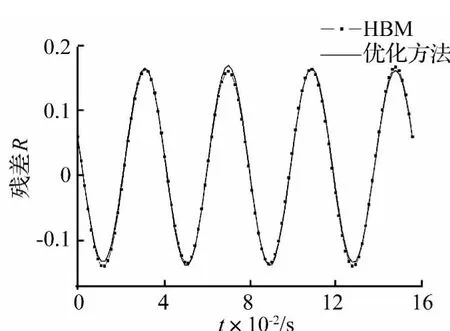
圖7 揮舞方程殘差曲線Fig.7 Flapping equation residual curve

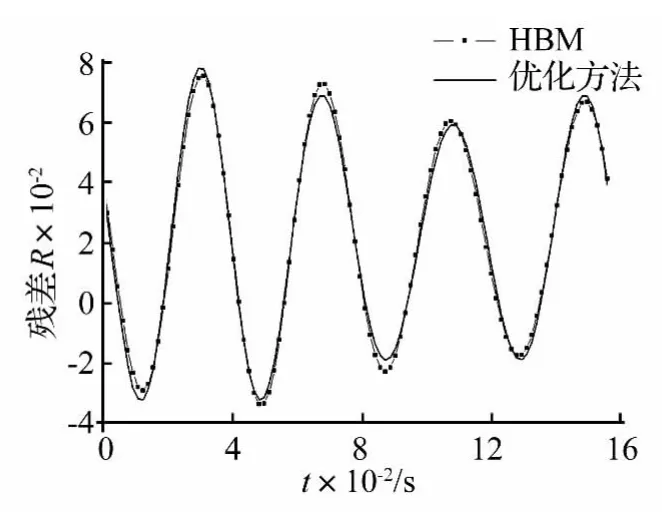
圖8 擺振方程殘差曲線Fig.8 Lagging equation residual curve

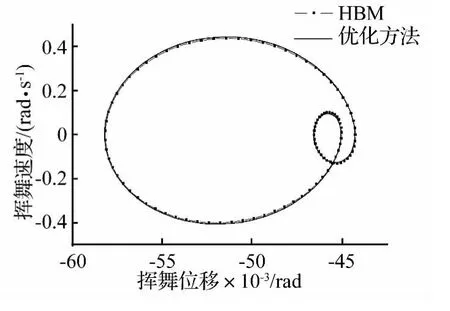
圖9 揮舞相圖Fig.9 Flapping phase graph

當前進比為0.1時，將各參數無量綱化后代入方程(14)。為降低方程維數、節省求解時間，計算時取槳葉前六階固有模態，將式(14)轉化為模態坐標方程，整理成狀態方程形式如下:

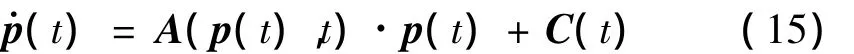
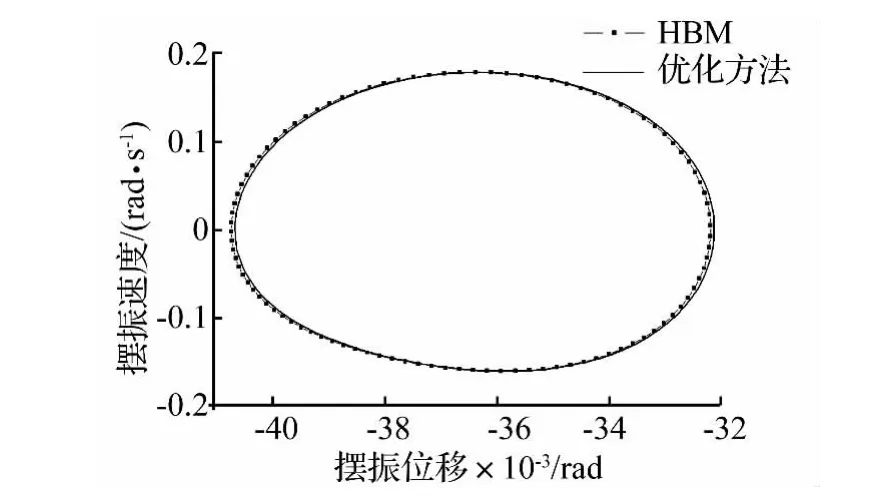
圖10 擺振相圖Fig.10 Lagging phase graph

圖11 槳葉的空間有限元Fig.11 Blade space finite element

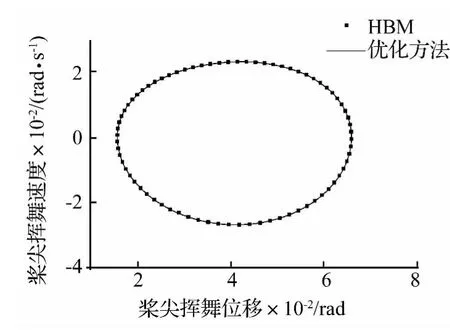
圖12 槳尖揮舞相圖Fig.12 Blade-tip flapping phase graph

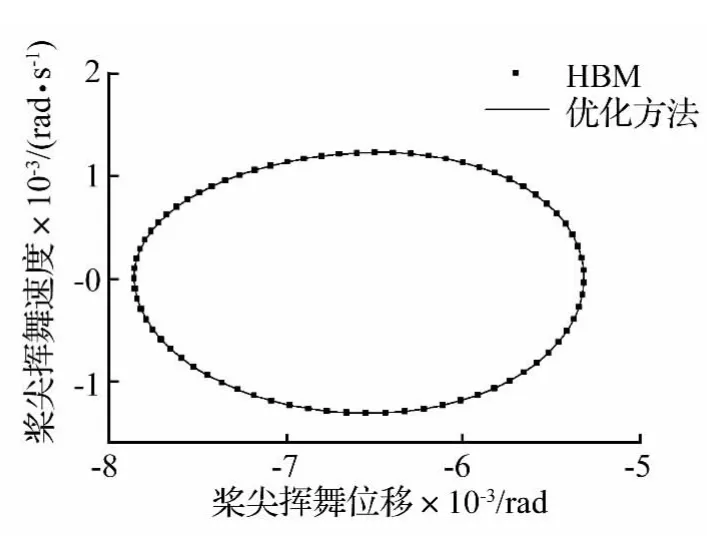
圖13 槳尖擺振相圖Fig.13 Blade-tip lagging phase graph

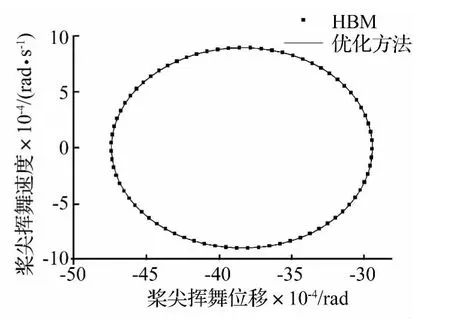
圖14 槳尖扭轉相圖Fig.14 Blade － tip torsion phase graph

將系統(15)在周期解p(t)處施加小擾動，求得線化系統 Floquet乘子的模分別為 0.441，0.093，0.192，0.576，0.107 和0.153，均小于 1，所以該旋翼系統在前進比為0.1時的周期響應漸近穩定。

3 結論

本文提出了一種求解非線性振動系統周期解的切比雪夫級數方法，將未知狀態矢量用切比雪夫級數表示，相當于考慮了系統中高階諧波的影響，因而求解時能夠獲得較高精度。方法中的優化問題還可等價于直接求解切比雪夫系數的含約束非線性最優化問題，但在相同條件下會增加計算復雜度。通過計算剛性鉸接式與彈性無鉸式旋翼的周期運動，表明將切比雪夫級數理論引入直升機氣彈響應和穩定性研究正確、可行，在求得的周期解誤差較小時更利于獲得系統較準確的FTM。

［1］Dunne J F，Hayward P.A split-frequency harmonic balance method for nonlinear oscillators with multi-harmonic forcing［J］.Journal of Sound and Vibration，2006，295:939－963.

［2］Chen Y M，Liu J K.A new method based on the harmonic balance method for nonlinear oscillators［J］.Physics Letters A，2007，368:371－378.

［3］ Cochelin B，Vergez C.A high order purely frequency-based harmonic balance formulation for continuation of periodic solutions［J］.Journal of Sound and Vibration，2009，324:243－262.

［4］ Grolet A，Thouverez F.On a new harmonic selection technique for harmonic balance method［J］.Mechanical Systems and Signal Processing，2012，30:43－60.

［5］Lu C J，Lin Y M.A modified incremental harmonic balance method for rotary periodic motions［J］.Nonlinear Dynamic，2011，66:781－788.

［6］唐進元，陳思雨.阻尼和剛度項含時變參數的強非線性振動系統周期解研究［J］.振動與沖擊，2007，26(10):96－100.TANG Jin-yuan，CHEN Si-yu.Study on periodic solutions of strong nonlinear systems with time-varying damping and stiffness coefficient［J］.Journal of Vibration and Shock，2007，26(10):96－100.

［7］ Hu H，Tang J S.A convolution integral method for certain strongly nonlinear oscillations［J］.Journal of Sound and Vibration，2005，285(45):1235－1241.

［8］張琪昌，趙薔薇，王煒.強非線性振動系統的通用化求解程序及應用［J］.振動與沖擊，2012，31(8):1－4.ZHANGQi-chang，ZHAO Qiang-wei，WANGWei.Universal solving program and its application in a strongly nonlinear oscillation system［J］.Journal of Vibration and Shock，2012，31(8):1－4.

［9］李銀山，李樹杰.構造一類非線性振子解析逼近周期解的初值變換法［J］.振動與沖擊，2010，29(8):99－102.LI Yin-shan， LI Shu-jie. Method of initial-value transformation for obtaining approximate analytic periods of a class of nonlinear oscillator［J］.Journal of Vibration and Shock，2010，29(8):99－102.

［10］ Zhou T，Xu JX.Research on the periodic orbit of nonlinear dynamic systems using Chebyshev polynomials［J］.Journal of Sound and Vibration，2001，245(2):239－250.

［11］Feng Z X，Xu X，Ji S G.Finding the periodic solution of differential equation via solving optimization problem ［J］.J Optim Theory Appl，2009，143:75 －86.

［12］胡海巖.應用非線性動力學［M］.北京:航空工業出版社，2000.

［13］陳洋洋，燕樂緯，佘錦炎，等.非線性自治振動系統同宿解的廣義雙曲函數攝動法［J］.應用數學和力學，2012，33(9):1064－1077.CHEN Yang-yang， YAN Le-wei， SZE Kam-yim， et al.Generalized hyperbolic perturbation method for homoclinic solutions of strongly nonlinear autonomous systems［J］.Applied Mathematics and Mechanics，2012，33(9):1064－1077.

［14］ Johnson L W，Riess R D.On the convergence of polynomials interpolating at the zeros of Tn(x)［J］.Math Z 1970，116(4):355－358.

［15］ Berrut J，Trefethen L N.Barycentric Lagrange interpolation.SIAM Rev，2004，46(3):501 －507.

［16］ Clenshaw C.The numerical solution of linear differential equations in Chebyshev series［J］.Proc Camb Philos Soc，1957，53:134－149.

［17］ Redkar S，Sinha S C.Reduced order modeling of nonlinear time periodic systems subjected to external periodic excitations［J］.Commun Nonlinear Sci Numer Simulat，2011，16:4120－4133.

［18］ Khasawneh F A，Mann B P，Butcher E A.A multi-interval Chebyshev collocation approach for the stability of periodic delay systems with discontinuities［J］.Commun Nonlinear Sci Numer Simulat，2011，16:4408 －4421.［19］ Celik I，Gokmen G.Approximate solution of periodic Sturm-Liouville problems with Chebyshev collocation method［J］.Applied Mathematics and Computation，2005，170:285－295.

［20］ Celik V.Collocation method and residual correction using Chebyshev series［J］. Applied Mathematics and Computation，2006，174:910－920.

［21］ Butcher E A，Bobrenkov O A.On the Chebyshev spectral continuous time approximation for constant and periodic delay differential equations［J］.Commun Nonlinear Sci Numer Simulat，2011，16:1541 －1554.

［22］Sedaghat S，Ordokhani Y，Dehghan M.Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials［J］.Commun Nonlinear Sci Numer Simulat，2012，17:4815 －4830.

［23］ Sinha S C，Pandiyan R.Analysis of quasilinear dynamical systems with periodic coefficients via Liapunov-Floquet transformation［J］.Int.J.Non-Linear Mechanics，1994，29(5):687－702.

［24］ Pandiyan R，Sinha S C.Analysis of time-periodic nonlinear dynamical systems undergoing bifurcations［J］.Nonlinear Dynamics，1995，8:21 －43.

［25］Sinha SC，Wu D H.An efficient computational scheme for the analysis of periodic systems［J］.Journal of Sound and Vibration，1991，151(1):91 －117.

［26］袁亞湘.非線性優化計算方法［M］.北京:科學出版社，2008.

［27］約翰遜W.直升機理論［M］.北京:航空工業出版社，1991.

［28］ Gunji B， Chopra T. University of Maryland advanced rotorcraft code(UMARC)theory manual［R］.UMAERO Report，1994.