兩外角平分線相等的三角形性質的探討

葉建耀

摘 要：如果三角形的兩個外角平分線相等，那么其是否為等腰三角形，針對這一點做著重論述，為相關教學工作者提供了一定的參考和借鑒。

關鍵詞：三角形；外角平分線；等腰三角形

一、兩外角平分線相等的三角形研究進展

在19世紀時學術界出現過這樣的命題：“兩內角平分線相等的三角形是等腰三角形。”據萊莫斯發現這個命題之后，對于這個命題正確與否的問題很難由幾何方法來實行證明，因此，也引發學術界對命題研究的興致。隨之而后，幾何學家斯坦納對這個命題做出了證明，并且得到了學術界的廣泛認同。隨后，人們的視線逐漸轉移，開始轉移到"三角形的兩個外角平分線相等是否是等腰三角形"的研究上，并于1989年蔣x先生解決了“位于一角對邊同側的另兩外角平分線相等的三角形是等腰三角形”的問題，此后人們對這個問題的討論也越來越激烈，但是卻沒有得到公認的方式證明出兩外交平分線相等的三角形為等腰三角形，故而本文對此作出證明研究，以求為相關教學工作者提供更多的證明方法。

二、三角形的兩外角平分線相等為等腰三角形的研究

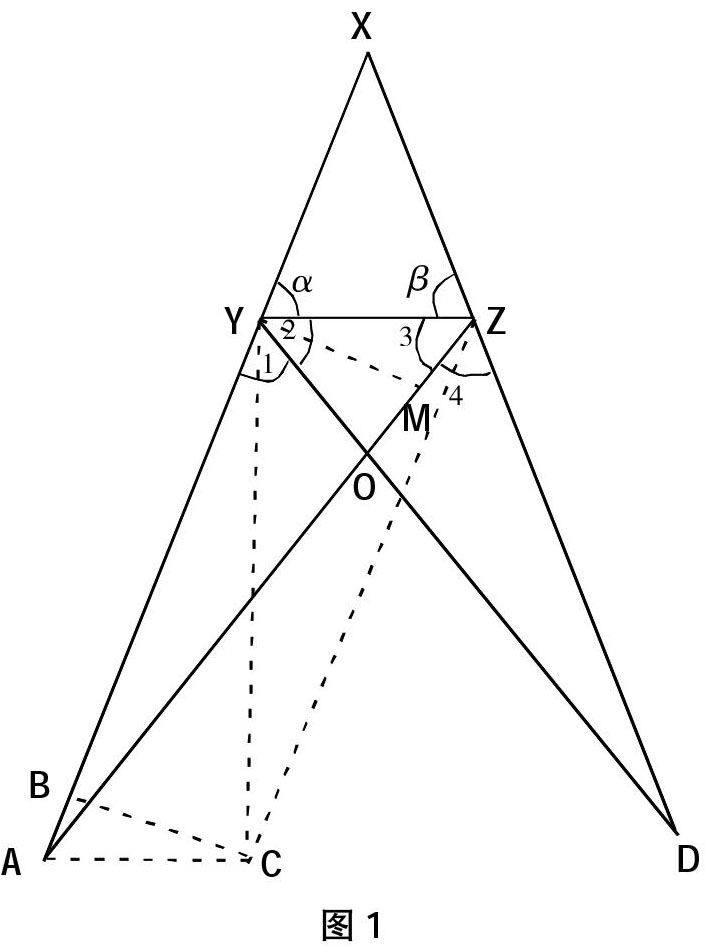
已知：△XYZ的旁心O與兩外角平分線YD和ZA在YZ邊的同側，YD=ZA，如圖1所示。

求證：XY=XZ或∠α=∠β

證明：過A、Z兩個點作∠ZAC=∠ZYD，∠AZC=∠D，與AC相交于C。

YD=ZA？圯△ZAC≌△DYZ？圯AC=YZ、ZC=ZD、∠YZD=∠ZCA

∵∠3=∠4=∠X+∠XAZ=∠X+∠YAZ

∠ZAC=∠2=∠1=∠X+∠D

∴∠YAC=∠YAZ+∠ZAC=∠YAZ+∠X+∠D

∠YZC=∠YZA+∠AZC=∠X+∠XAZ+∠D

由此？圯∠YAC=∠YZC.

然后過Y、C兩點作YM⊥ZC于M點，CB⊥YA于B點，連接YC后，Rt△ABC≌Rt△ZMY？圯YM=BC。由于YC=YC、YM=BC？圯Rt△YBC≌Rt△CMY？圯∠CYB=∠YCM？圯YA∥ZC？圯∠YAZ=∠CZA、∠D=∠AZC？圯∠YAZ=∠D

而△YOA和△ZOD中可以推出∠1=∠4？圯∠2=∠3？圯∠1+∠2=∠4+∠3？圯∠α=∠β？圯XY=XZ

∴△XYZ為等腰三角形

在上述論證中，證明了三角形兩個外角平分線相等的情況下，此三角形為等腰三角形，這樣的方法并不是唯一的論證方法，教師在展開教學活動中應從多個方面切入，注重的是培養學生的邏輯推理能力，而非固定的“論證方法”灌輸，要注重培養學生的學習興趣，從而激發和加強學生的邏輯推理能力。

三、關于三角形平分線的初中教學

在初中教學的“三角形角平分線”中，其內角平分線是指三角形中的一個內角的平分線與它的對邊相交，這個角的頂點和交點之間的線段叫做三角形的角平分線，但是，學生在學習的過程中，由于對幾何的邏輯推理缺乏興趣，常常沒有很高的學習熱情，也導致學生學習成績無法有效提高，教師在教學工作中，應從以下幾方面考慮：

在三角形外角平分線的教學中，可以結合多媒體技術向學生展示論證過程，多媒體技術可以將圖片、文本、影視、聲音和教學相結合，這種方式的應用能打破幾何理論教學中的抽象性，通過營造一個擁有視聽的立體化環境，把教學中無法通過教師講解和分析表現出來的東西展示出立體可見畫面。比如，在初中幾何課堂中所講解的三角形平分線一課中，用傳統的講解方法只能局限于理論講解和論證分析，這樣的講解是概括抽象的，學生在學習的過程中由于思維缺乏對這具體現象的聯系，對于教師的講解，學生思維上只能發揮表層的“記憶”功能，無法對知識進行深入地分析和探究。因此，對多媒體技術的利用，可以需要論證的圖形展示清楚，把整個論證過程用動態的方式展現出來，從而營造出一個理想的學習環境，讓學生對初中幾何的學習能力得到提高和鞏固，這樣的教學方法是讓學生在幾何的學習過程中提高自身的科學素養，在社會的生活中學會用科學的眼光分析科學性現象，符合素質教育的宗旨。

要理解三角形外角平分線的知識，在教學中應滿足整個論證推理完整的前提下盡量簡化論證的過程，可以讓學生對復雜的論證方法進行簡單的掌握，然后再由易入難。因此在運用這樣的教育模式開展教學工作中，不應只局限于對教材的理論分析，可以讓學生利用多媒體技術加深幾何知識在社會生活中的實際運用。比如，學生在學習幾何的課程中，三角形外角平分線相等為等腰三角形這些命題是誰發現的，在教材中并沒有具體描述，因此，可以讓學生通過互聯網的平臺去搜索相關知識，可以通過微博、論壇等渠道去發表對幾何的評論，通過對幾何的發展歷程的研究，讓學生利用多媒體技術去自主展開學習探討，引導學生在學習過程中發現科學技術的人文精神，提高了辯證唯物主義教育的效果，能有效培養學生對幾何的學習興趣。

從教育改革的層面上看，多媒體技術結合的幾何教學是一種未來教育的發展趨勢，我們可以采用與多媒體技術相結合的教學方式去對學生進行更直觀立體的教學，對于圖形的論證可以產生詳細的動態描繪，同時注重學生的邏輯能力培養，充分發揮學生自主學習能力的積極性，可以讓學生在這樣的教學中獲得創新的動力，是培養學生創新能力的有效措施。

參考文獻：

[1]王彥海.關于Steiner-Lehmes定理外等長分角線的猜想的研究[J].烏魯木齊成人教育學院學報，2010（3）：82-85.

[2]洪盈平，崔樹峰.斯坦納定理推廣猜想的證明及再討論[J].安康師專學報，2010：93.

[3]敬坤.三論三角形外解平分線三角形的性質[J].數學教學通訊：上半月，2011（9）.

（作者單位 福建省莆田市莆田哲理中學）