省編數學教材“數列”編寫意圖及教學建議

丁陽

【摘 要】該文從分析比較新舊教材入手，以數列部分為例，剖析新舊教材的基本理念以及新舊教材的結構和難度，以求有助于中職數學老師理解新教材的編寫理念，轉變傳統的教育和教學觀念，改變傳統的灌輸性教學方式，更好地使用新教材。

【關鍵詞】數列 模塊 信息化教學 課程難度

新中職教學大綱要求貫徹“以服務為宗旨，以就業為導向”的職業教育辦學方針，堅持以學生為主體的教學理念，著眼于學生的全面發展，在培養高素質勞動者和技能型人才上發揮應有的作用。按照教育部2009年頒布的新教學大綱要求編寫的新教材，由于與舊教材差別較大，許多教師在不同層面產生了困惑，依然使用舊教材、舊方法組織教學，偏離新教材編寫意圖。鑒于此，筆者在對“數列”部分進行表層結構、深層結構及難度比較分析的基礎上，提出新教材“數列”部分的教學建議。

一、數列部分表層結構的分析

數列部分在基礎模塊中是第六章，所占篇幅為30頁。涉及的知識點包括：數列的定義、等差數列的定義、等差數列通項公式、等差數列前n項和公式、等比數列定義、等比數列通項公式、等比數列前n項和公式。本教材模塊設置及特點分析如下：

1.課前導入模塊。在章前導入部分，教材通過三個例子意在指出，古今中外，不論是生活還是科學，都能看見數列的影子，數列扮演著重要的角色。本章學習目標和本章目錄設置的意圖在于使讀者明確本章內容的廣度與深度，明確學習的內容與目標。

2.思考交流模塊。從模塊設置中我們可以看出，新教材與舊教材相比，最大的區別就在于采用了“探究——思考交流——問題解決”模式。新教材中的探究性學習模式主要是指情境探索學習，體現的思維比較發散，問題的答案一般不唯一，教材中一般不會為設置的問題提供解答或提示，要靠學生經過自己的思考以及交流討論獲取答案。

3.習題模塊。新教材是一個知識點對應安排一個練習，并注意學后練習鞏固，每一小節安排一個習題，習題量較少，而且一般是例題的變式或加深題，題量一般不超過10個，全章安排一個復習題，復習題分為A、B兩組，A組為基礎題，B組為加深題，并且復習題的題量較大。新教材在處理等差中項和等比中項的內容時，沒有安排相應的例題，只是把等差中項和等比中項的概念以及習題放在復習題B組中。

4.閱讀模塊。閱讀模塊目標：體現數學美，滲透數學文化，了解數學研究新分支——分形幾何，感悟大自然中的數學現象。與舊教材相比，新教材閱讀模塊更有趣味性和科學性。新教材“數列”部分的閱讀材料是雪花問題，這首先是一種數學文化的滲透，介紹了數列在數學發展史上的成就，并且可以通過雪花問題鍛煉學生的觀察能力和空間想象能力，通過這種趣味性的材料引導學生將計算機與數學相結合，培養學生信息化意識，提高學生的應用能力。

5.小結模塊。新教材的“回顧與小結”整體篇幅小，其突出特色是配有直觀的章節知識框架圖，并且以精練的語言高度概括了本章的內容要點和其中蘊涵的數學思想方法。教師利用章節知識框架圖可以使學生能夠整體把握本章的知識點，并用類比的方法更加透徹地理解本章內容。

二、數列部分深層結構的分析

新教材中，數列一章一共配有8幅插圖，新教材中的插圖一般都是在探究模塊出現，與探究問題的內容相結合，對文字起到了很好的輔助作用，同時也使得學生更加容易理解文字的內容，通過形象生動的圖片引起學生注意，激發學生學習的興趣。“探究——思考交流——問題解決”是新教材的最大亮點，新教材設計了許多不同形式的探究活動，這些都有助于對學生數學思維和數學方法的培養。所謂數學思維，就是指教師在教學活動中，根據數學素材引導學生進行數學形象化的數學構思，形成數學運算。而數學方法是以數學為工具進行科學研究的方法，即用數學語言表述事物的狀態、關系和過程，并加以推導、演算和分析，以形成對問題的解釋、判斷和預測的方法。

新教材在開篇“數列的概念”這一知識點的內容展開中，給出了三個探究問題（見教材P2），拋出這三個問題的意圖就是想讓學生根據生活實例，使用數學語言表述相關問題，抽象歸納出一般性的數學概念，讓學生使用猜想、歸納、抽象等方法，經歷整個數學思維過程，使知識內化，形成新的知識結構。

數學思想主要是指數學本身的形成、論證、運算及應用的思想，主要是對數學基礎知識和基本方法的本質概括，是在反復理解運用數學概念和方法的基礎上形成和發展的。數列雖篇幅不長，但其中蘊含了豐富的數學思想。在解答數列中的有關問題時，充分利用數學思想方法會達到事半功倍的效果。教師應借助例題講演，讓學生領悟并學會應用“數形結合法”與“函數轉化法”。

三、新舊教材課程難度比較分析

我們定義影響課程難度（用N表示）三要素：課程的深度、廣度和課程時間。其中，課程廣度（用G表示）就是指課程中包含的知識點的多少，我們用知識點的數量來表示；課程深度（用S表示）則是指各個知識點的掌握程度，我們用大綱要求的不同程度來表示；課程實施時間（用T表示）是指按照教學計劃的課程內容的安排時間，用大綱中的“課時”來表示。這樣，我們可以建立課程難度的數學模型如下所示：

N=λ·G/T+（1-λ）·S/T

在這個模型中，其中G/T表示單位時間的課程廣度，S/T表示單位時間的課程深度，λ稱為加權系數，且滿足0<λ<1。

1.難度模型的相關說明。

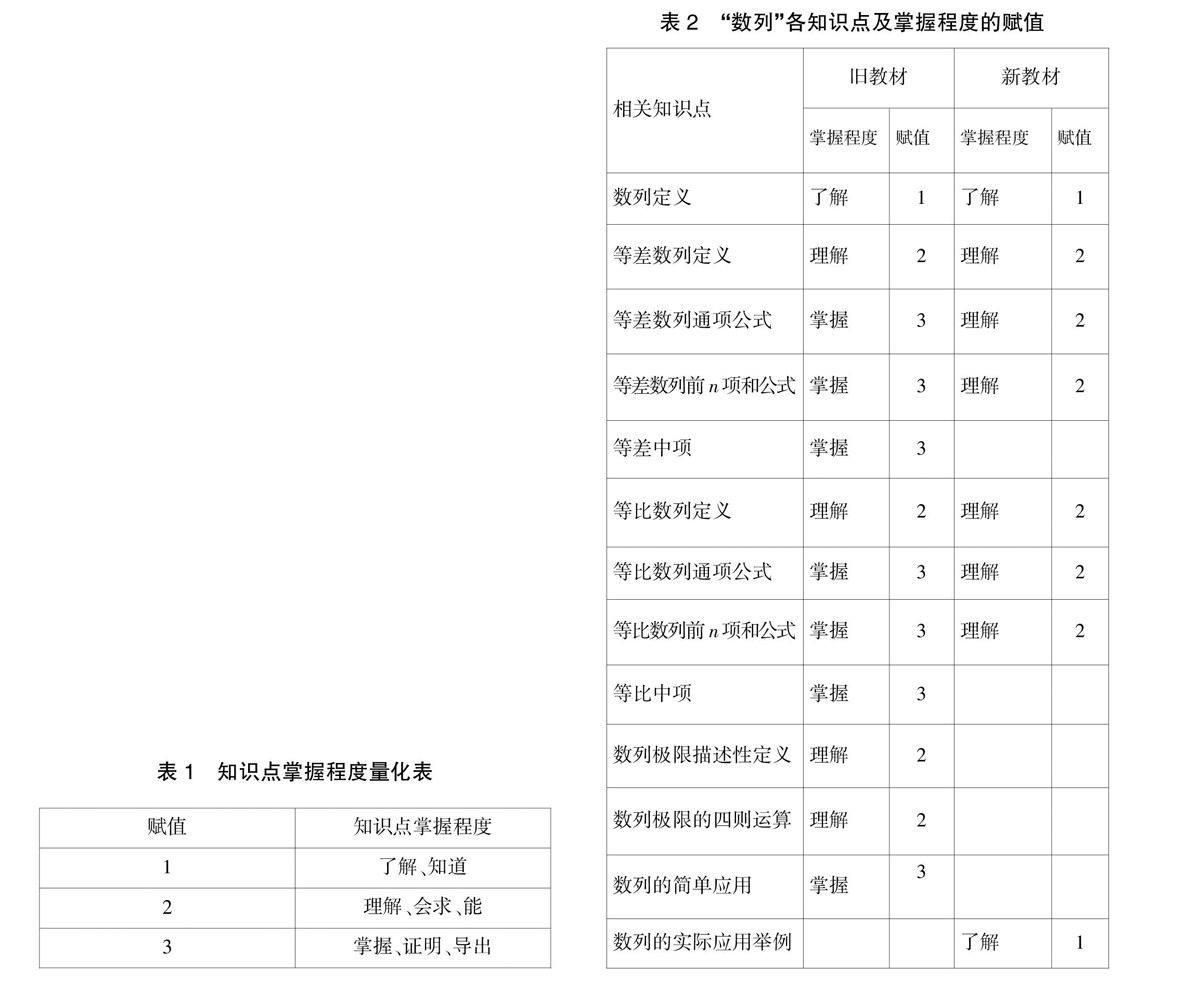
（1）課程廣度。為了量化新舊教材數列部分的廣度，我們用數列的知識點的個數來量化。因為新舊教材都是依據大綱編寫的，故我們根據大綱中數列部分的內容進行統計。

（2）課程深度。由于大綱對各個知識點的要求不同，我們根據大綱要求將不同的認知要求進行賦值，以此量化課程深度，如表1所示。

表1 知識點掌握程度量化表

（3）λ的取值。λ是一個經驗常數，根據現有研究成果，專家學者普遍認為課程廣度對課程難度的影響較大一些，故取值為λ=0.6。

2.新舊教材數列部分課程難度的量化比較。數列部分課程時間的確定。根據舊教材數列部分內容的課時安排情況確定為14課時，即T1=14；而新教材數列部分內容的課時安排總計10個課時，即T2=10。

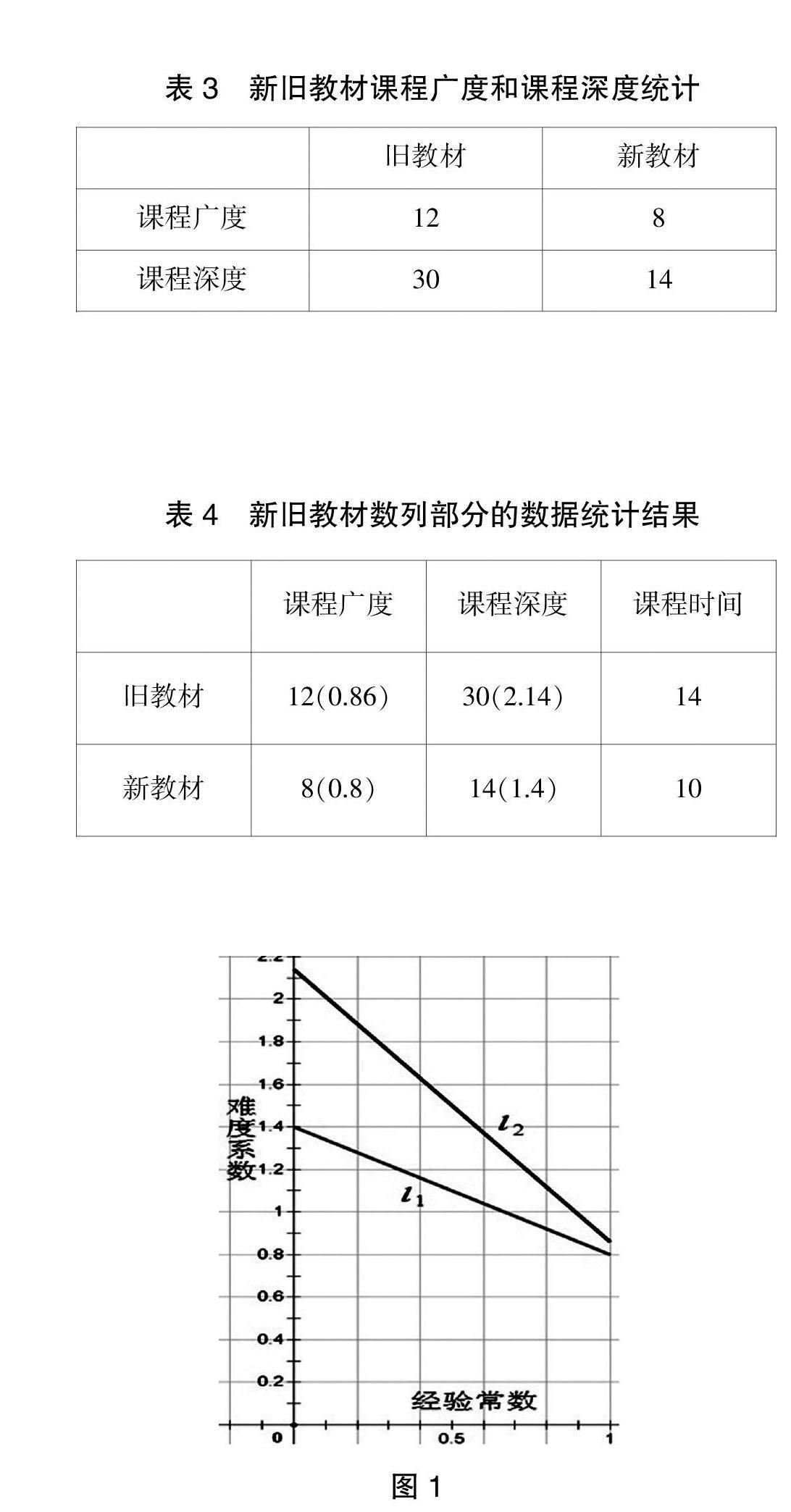
根據上文中確認知識點以及賦值法，我們將新舊教材數列部分的知識點及對知識點的掌握程度用表2羅列出來。根據此表數據，可以得出新舊教材課程廣度和課程深度（見表3），并可以分別求出兩本教材中數列部分的可比廣度和可比深度（見表4）。

表2 “數列”各知識點及掌握程度的賦值

表3 新舊教材課程廣度和課程深度統計

舊教材的可比廣度為G1/T1=0.86，可比深度為S1/T1=2.14；新教材的可比廣度為G2/T2=0.8，可比深度為S2/T2=1.4。

表4 新舊教材數列部分的數據統計結果

所以根據所建立的模型，分別表示出新舊教材數列部分的課程難度：

N1=0.80·λ+1.40·（1-λ）=1.4-0.6·λ

N2=0.86·λ+2.14·（1-λ）=2.14-1.28·λ

由于0<λ<1，故0.8

如果λ=0.6，那么N1=1.04，N2=1.37。

3.新舊教材數列部分課程難度對比結論。

由圖1可以看出，直線l1表示新教材數列部分課程難度系數值N1，直線l2表示舊教材數列部分課程難度的N2，由于0<λ<1，無論λ如何取值，線段l1始終在線段l2的下方。

結果表明，與舊教材數列部分的難度相比，新教材的難度有所下降，這主要是因為新教材數列部分的課程廣度以及課程深度都比舊教材的要低。

四、新教材使用教學建議

新大綱倡導的數學教學是師生之間、生生之間交流互動與共同發展，讓學生都能獲得必需的數學知識，使學生得到全面發展。以下幾點教學建議僅供教師使用新教材時參考。

1.新教材使用時，教學要突破“定義-定理-證明”的傳統教學方式，不必拘泥于嚴格的演繹推理，可從具體的生產或生活實例進行探究引入課題，導出相關概念，關注學生的直覺感受和已有經驗，并把它們提升到數學理論的高度。挖掘“思考交流”的深度，使學生真正內化知識，形成新的認知結構。充分利用“問題解決”強化學生應用數學的意識，強化學生用數學的眼光看世界的能力。

2.按照大綱的要求，數列概念的引入、等差數列、等比數列的學習都要結合學生生活實例和不同專業背景來進行設計。因此，教師在教學的過程中要精選一些典型的、適合學生的生活情境，從實際應用的角度去引出概念，調動學生的學習主觀能動性，提高教學效率。

3.本章節的重點是等差數列和等比數列。等差數列和等比數列在知識內容和思想方法上都很相似。在學習了等差數列后，建議教師引導學生用比較學習法，類比于等差數列的通項、性質以及前n項和等，自主探索等比數列的相應問題。

4.關于信息化教學的引入。根據教學大綱要求，培養學生計算工具使用技能。信息化時代智能化計算工具的使用應該成為學生的必備技能。本章節借助計算機輔助教學，可以在學習過程中起到化繁為簡的作用，如“正方形篩子”的建立等。

5.本章節的“探究”“問題解決”以及例題和習題中，有許多來源于古代數學和現代數學的素材，如“出門望九堤”“雪花問題”等，還有很多來源于實際生活情境，體現了數學文化價值的題目，如“麥田怪圈”“分形幾何學”等。教學中要注意加強與實際生活的聯系，同時也要注意利用這些資源，提高學生學習本章節內容的興趣，調動學生學習的積極性和主動性。

（作者單位：江蘇省連云港中等專業學校）