基于星間星地鏈路的整網批處理定軌算法仿真研究＊

楊遵龍，董緒榮，李曉宇

（裝備學院，北京101416）

0 引 言

聯合定軌是指對于具有星間鏈路的導航星座，聯合星間測量和星地測量數據，通過統一融合處理，同時估計所有衛星的軌道參數。批處理定軌法是在觀測結束后，結合某一單個歷元所有觀測信息求此歷元狀態變量的“最佳”估計。批處理方法的觀測數據多，且具有統計特性，因此解算精度較高，但算法計算耗時，不適于作實時定軌［1－2］。利用批處理算法進行高精度的事后處理。

整網批處理定軌方法，即聯合星間觀測信息與星地觀測信息，通過使用批處理算法進行整網平差的過程。在本文中基于星間星地鏈路的整網批處理定軌方法簡稱為星地整網定軌方法。

1 系統模型建立

1.1 星地偽距觀測方程

假設測量過程中地面設備延遲已經過標校，則模型寫為

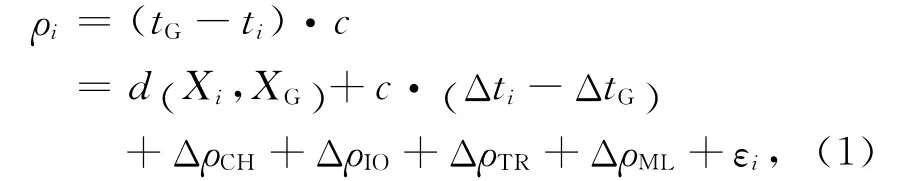
式中：ρi表示地面站G對衛星i的測量偽距；c表示光速；Δti表示衛星i的鐘差；ΔtG表示地面站的鐘差，由站間時間同步確定；ΔρCH表示衛星i發射機延遲差；ΔρIO表示電離層延遲誤差；ΔρTR表示對流層延遲誤差；ΔρML表示多徑效應；εi表示接收機熱噪聲；d （Xi，XG）＝ ［（Xi－XG）2＋ （Yi－YG）2＋（Zi－ZG）2］1／2表示兩點之間幾何距離；Xi、XG分別表示衛星i和地面站G在慣性系中的位置。

觀測殘差（O－C）表示為

1.2 星間偽距觀測方程

在此給出僅含衛星距離和鐘差信息的改化偽距

式中：d （Xi，Xj）表示衛星i、j之間的幾何距離；v表示觀測誤差，包括隨機誤差和未能消除的所有其它誤差之和［3］。

觀測殘差（O－C）的形式為

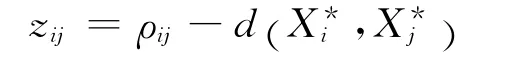
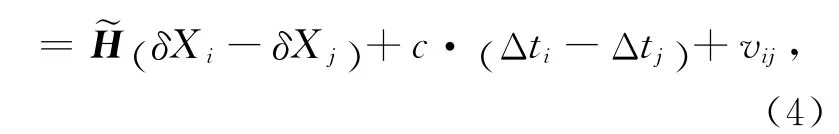
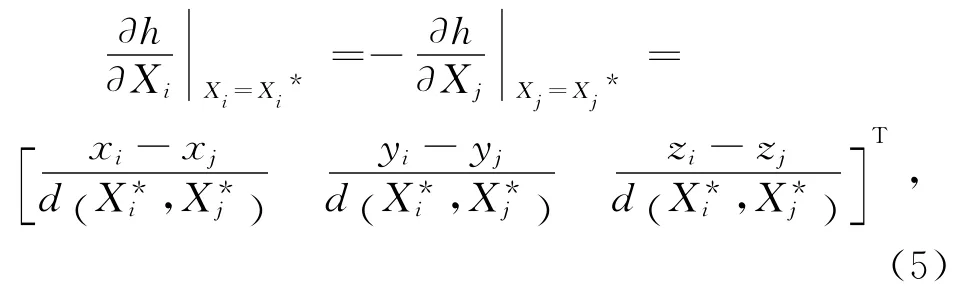
1.3 批處理算法

批處理定軌的基本方法是，將某觀測弧段［t0，t］上得到m維觀測值（包括星地和星間觀測值）z＝［z1z2…zm］，通過狀態轉移矩陣歸算到某一歷元（如初始歷元t0）。

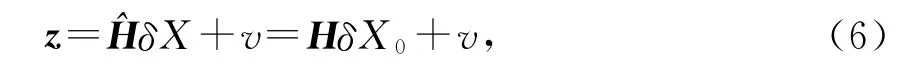
式中：z對應于式（2）或式（4）的星地或星間觀測殘差；X對應于軌道狀態；因此，問題可化為求解t0時刻的最佳估計，這是一個典型的線性最小二乘問題。在工程應用中一般作Gauss－Markoff假設［4］

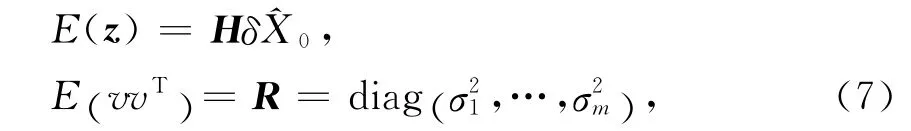
由于觀測方程（6）中含有測量誤差，工程中需要采用加權最小二乘估計方法，以保持盡量多的有用信息。問題描述為求x∈Rn，滿足

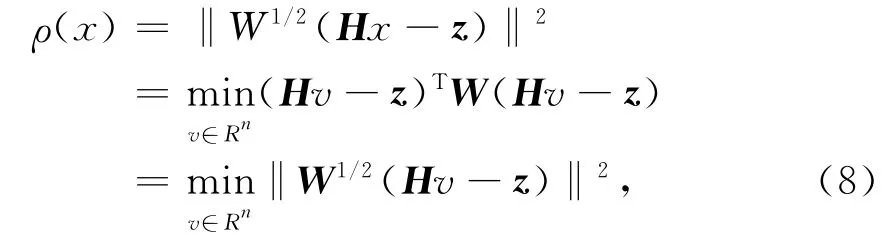
式中，W為實對稱權矩陣，在應用中可取W＝R－1.

式（8）的極小范數解為

式中，B＝（W1／2H）－W1／2為矩陣H的加權廣義逆。

2 批處理定軌計算過程

在進行導航衛星定軌計算過程中，所采用的狀態方程和觀測方程都是基于參考軌道進行線性化處理后的模型，所以其非線性部分會造成定軌結果的偏差。在批處理定軌中通過多次迭代來解決此問題。設置的收斂準則［5］為

1）衛星位置矢量最新估值的方差小于預先指定的判據POS.即

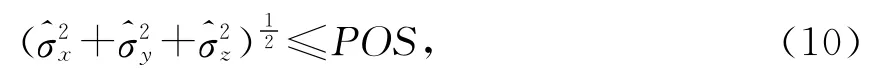
2）觀測殘差的均方差滿足

式中：ε為預先指定的一個小量；RMS為觀測殘差均方差；RMS＊為觀測殘差均方差的線性預報值［6］。

RMS、RMS＊定義為［6］

式中：vk為第k次迭代中觀測數據的殘差；為對參加估值的觀測數據的權和。

當滿足任意一個條件（10）或（11）時，再迭代一次即認為估計過程正常收斂而終止。設k＋1次迭代收斂，則被估狀態的最優估值為

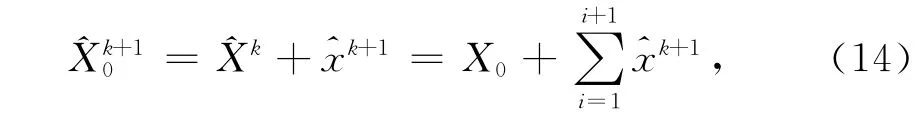
式中，X0為估計狀態矢量的先驗值。

參照批處理定軌的一般過程［7］，整網批處理定軌的主要過程描述如圖1所示。

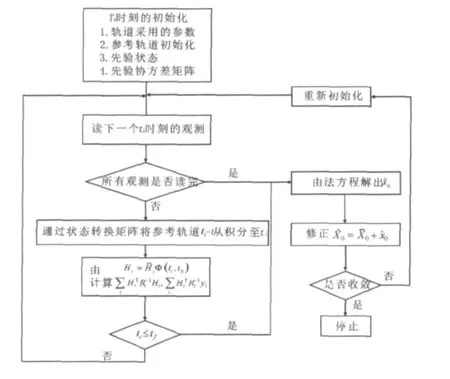
圖1 批處理定軌算法流程

3 基于星地整網批處理定軌算法的仿真分析

3.1 仿真條件

星 座 構 型：Walker24／3／2：55°，軌 道 高 度：215 00km，軌道傾角55°［6］.考慮星間測距誤差0.5 m，波束角為30～60°；星地測距誤差3.0m，截止高度角10°，不考慮傳播時延及鐘差。定軌弧長：7天。

3.2 仿真算例設計

在進行星地整網定軌計算時，觀測數據的來源分為星地測距信息和星間測距信息。為分析星地測距信息的加入及地面區域布站的位置和數量對批處理定軌精度產生的影響，本章進行如下算例設計，如表1所示。

表1 星地整網批處理定軌仿真算例

在算例1與算例2中，采用傳統地基方式進行定軌時分別采用了全球17測站和全球34測站的跟蹤觀測方案。其地面測站分布參照IGS全球測站分布位置設置，選取部分站位。其中全球17個測站代號分別為：ALGO、ALIC、ASPA、BAHR、BJFS、CIC1、DGAR、GLPS、GUAM、HARB、KOKB、LPGS、MAS1、OPMT、THTI、WUHN、ZIMM。全球34個地面測站代號分別為：ALGO、ALIC、ARTU、BAHR、BJFS、BRUX、CHUR、CIC1、CRO1、DARW、DGAR、GLPS、GUAM、GUAO、HARB、HOFN、KERG、KOKB、KOUR、KUNM、LHAZ、LPGS、MAC1、MANA、MAS1、MBAR、MDVJ、NKLG、NOT1、NRIL、OHI3、ONSA、OPMT、PERT。其具體地理坐標位置可在IGS網站中查詢。

在分析地面測站的數量及分布對批處理定軌精度的影響時，選用了IGS在國內合作的5個地面測站。具體位置如表2所示。

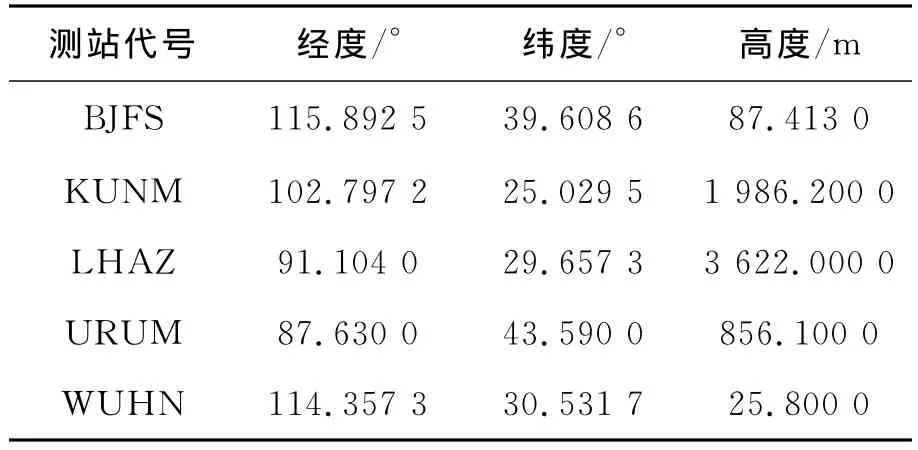
表2 國內5個地面測站地理坐標

3.3 仿真結果與分析

星地整網定軌的仿真結果以平均RMS值作為指標，其定義為

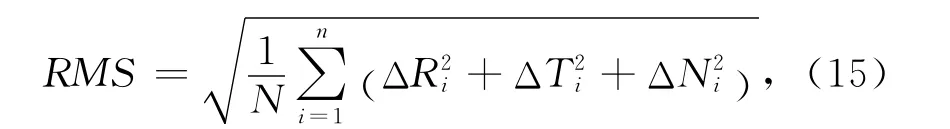
式中：N為觀測歷元總數；ΔR為軌道徑向誤差；ΔT為軌道沿跡向誤差；ΔN為軌道法向誤差。

算例1：圖2示出了分別采用全球17個測站及全球34個測站進行傳統地基定軌的第1天至第7天軌道RMS全星座統計值。條形圖值代表所有全星座衛星軌道的徑向、切向及法向三維RMS統計結果；“mean”表示了7天的平均值。圖3示出了采用兩種不同數量地面測站進行地基定軌的第1至第7天軌道RMS差值。

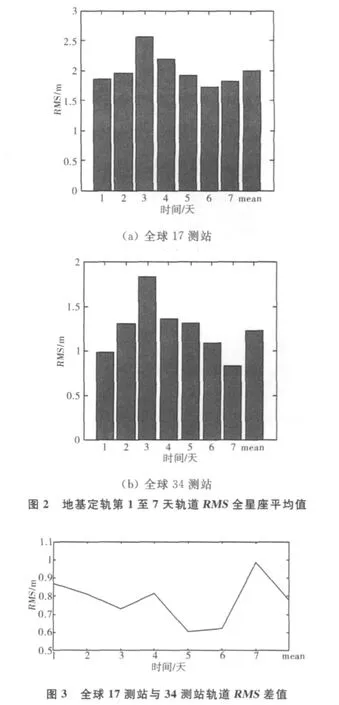
圖4與圖5示出了分別采用全球17個測站和34個測站進行傳統地基定軌的第1天的所有衛星軌道RMS統計值。

圖6示出了采用兩種不同數量地面測站進行地基定軌的第1天軌道RMS差值

分析：從圖中可以看出利用全球34測站進行傳統地基定軌，其RMS精度明顯高于利用全球17測站的地基定軌結果。34測站地基定軌的軌道平均RMS為1.24m；17測站地基定軌的軌道平均RMS為1.99m.這是因為當地面測站合理增多時，導航衛星的幾何精度好，觀測數據的增多使得空間約束增強。

算例2：為了分析星地整網批處理定軌精度，加入了星間觀測信息，并對地面測站布設的不同組合進行仿真分析。具體方案設計及相應全星座RMS平均值如表3所示。

表3 星地整網定軌軌道RMS全星座7天平均值

圖7示出了方案1～7對衛星進行星地整網定軌的第1至7天軌道RMS的全星座平均值。

圖7 整網定軌第1至7天軌道RMS全星座平均值

分析：從以上圖、表可以看出：

1）全球分布測站及國內局域測站的整網定軌精度都較高，軌道RMS均優于1.0m，相對于全球34站和17站的傳統地基定軌結果有較大提高。由于星間鏈路信息加強了衛星沿跡向與法向的幾何約束，定軌誤差顯著減小。

2）全球分布測站的整網定軌精度要稍高于國內測站整網定軌精度，國內局域測站進行整網定軌的各種方案結果精度相差不大。在相同的星間鏈路構型中，相比于全球布站，局域布站的幾何精度相對較差，因此精度稍低。

3）國內局域測站進行整網定軌，其7天平均RMS值度與測站數無顯著對應關系，但是地面測站越多，單天定軌結果差異越小，表現越穩定。

4 結 論

導航星座衛星對軌道確定的精度和自主性要求較高，采用傳統的地基定軌方法已不能滿足需求，但若完全依靠星間相互測量偽距定軌則又存在星座網的基準秩虧問題。提出了基于星間星地鏈路的整網批處理定軌方法。由仿真結果可知在地面系統支持下，星地聯合整網估計的精度遠高于傳統定軌精度，定軌精度主要取決于星間觀測的精度。適當增加地面測站時，導航衛星的幾何精度好，觀測數據的增多使得空間約束增強，可以提高定軌精度。

［1］ 朱 俊，廖 瑛，文援蘭.基于星間測距和地面發射源的導航星座整網自主定軌［J］.國防科技大學學報，2009，31（2）：15－21.

［2］ 胡小平.自主導航理論與應用［M］.長沙：國防科技大學出版社，2002.

［3］ 周建華.序貫處理與成批處理在定軌應用中的一些問題［J］.測繪學，1993，22（2）：142－148.

［4］ ANANDA M P，BERNSTEIN H，CUNNINGHAM K，E，et al.Global positioning system（GPS）autono－mous navigation［C］／／IEEE Position Location and Navigation Symposium，las Vegas，1990：435－455.

［5］ 林益明，秦子增，初海彬.基于星間鏈路的分布式導航自主定軌算法研究［J］.宇航學報，2110，31（9）：2088－2094.

［6］ OLIVE M，EBERHARD G.Satellite orbits Models，methods，and application［M］.2nd ed.Verlag Berlin Heideberg New York：Springer，2001：208－218.

［7］ WEN Yuantan，ZHU Jun，LI Zhi，et al.Simulation and analysis of integrated orbit determination of satellites constellation［J］ .Journal of Astrooeutics，2009，30（1）：155－163.

［8］ 張育林，范 麗，張 艷.衛星星座理論與設計［M］.北京：科學出版社，2008.