基于免疫遺傳算法的線狀要素圖形簡化方法研究

馬瀟雅，郭慶勝，2

（1.武漢大學資源與環境科學學院，湖北武漢 430079；2.武漢大學測繪遙感信息工程國家重點實驗室，湖北武漢 430079）

一、引 言

作為占地圖圖形80%以上的地圖目標，線狀要素的自動綜合自然成為地圖綜合的一個重要方面。圖形簡化作為其綜合的重要手段之一，已得到國內外有關學者的持續關注，并研究實現了大量自動化算法［1-4］，如著名的道格拉斯算法、Li-Openshaw算法等。隨著智能優化算法的廣泛應用，有關學者在線狀要素圖形簡化的智能優化算法探索中也已取得一定成效，提出了基于遺傳算法［5］和蟻群優化算法［6］的線狀要素圖形簡化模型，并證明了智能優化算法是解決線狀要素圖形簡化問題的一個有效途徑。

免疫遺傳算法是人工免疫系統模型的重要組成部分，該算法將免疫系統生理學機制和自然生物進化機制相結合，具有強大的空間搜索能力［7-8］，在優化問題的解決上具有很大優勢。本文在現有線狀要素圖形簡化的研究基礎上，提出一種基于免疫遺傳算法的線狀要素圖形自動簡化方法。并將試驗結果與單純免疫算法、遺傳算法和道格拉斯算法進行對比，試驗表明基于免疫遺傳算法的線狀要素圖形簡化方法在保持線狀要素圖形形狀方面表現更佳。

二、基于免疫遺傳算法的線狀要素圖形簡化方法

基于免疫遺傳算法的線狀要素圖形簡化的本質是將線狀要素圖形簡化問題轉化為抗原，線狀要素圖形簡化方案轉化為抗體，抗原和抗體間的親和力值則是衡量抗體與抗原的親和度，圖形簡化即為尋找與抗原親和度最高的抗體的過程。為達到保證數據質量和可視化要求的同時，盡可能減少曲線上的點數，并保留關鍵點（包括曲線的端點、極值點、拐點等）的圖形簡化目標［9］，本文依據免疫遺傳算法的基本原理，顧及線狀要素的幾何精度和形狀特征點保留的約束條件，引入不可行解的修復機制，提出線狀要素圖形簡化方法。

1.編 碼

編碼的本質是將線狀要素圖形簡化方案轉換成免疫系統中的抗體，并且每個抗體對應一種圖形簡化方案。本文采用二進制編碼構造算法的抗體，編碼的長度為線狀要素上節點的數目，每個基因位儲存該節點的狀態，0為舍棄，1為保留。同時，線狀要素的首尾兩個節點為必須保留點。

2.親和度函數設計

在采用免疫遺傳算法進行問題求解時，通常抗體的親和度高低反映了抗體（問題的解）滿足抗原（問題）的程度，即抗體的親和度值越大，抗體（問題對應的解）越優。在對線狀要素圖形簡化結果進行評價時，親和度函數的設計僅考慮保留點個數及特征點保留兩個約束條件，幾何精度的保證則通過引入不可行解的修復機制解決。

本文把對線狀要素圖形形狀的保持起重要作用的節點認為是線狀要素的形狀特征點，各節點的重要程度，由其貢獻值體現。根據文獻［10］的方法，各節點的貢獻值可通過該節點兩相鄰的直線段長度L（S1）、L（S2）及兩線段的轉角β（S1，S2）綜合計算得到［10］，計算公式如下

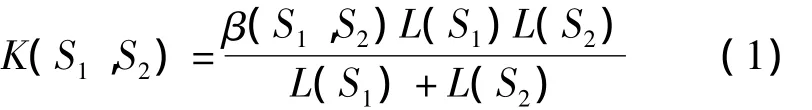
基于免疫遺傳算法是一個尋求保留節點的貢獻值最大、圖形表示節點個數最少，以及圖形簡化后在距離限差內應舍棄的保留節點個數最少的抗體的過程。該算法中抗體親和度值可通過式（2）計算得到

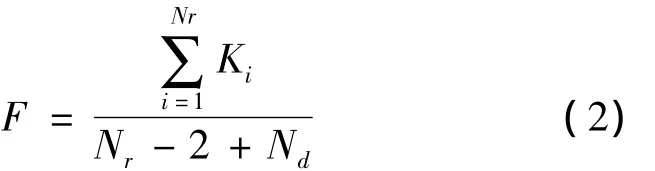
式中，Ki為線狀要素第i個保留節點的貢獻值；Nr為保留節點的個數；Nd為圖形簡化后距離限差內應舍棄的保留節點個數。其中，Nd的探測方法為:解碼抗體，沿線狀要素的數字化方向依次遍歷并計算各保留節點與其相鄰兩保留節點連線的垂直距離，且判斷該距離是否小于指定限差，是則說明該節點應被舍棄。

3.算法流程及主要算子設計

基于免疫遺傳算法線狀要素圖形簡化方法的流程如下:

1）隨機產生初始抗體種群Ab（0），令當前算法迭代次數為T=0。

2）對抗體種群Ab（k）執行克隆操作，得到新抗體種群Abc（k）。

3）對抗體種群Abc（k）執行高頻變異操作，得到新抗體種群Ab'c（k）。

4）對抗體種群Ab'c（k）執行交叉操作，得到新抗體種群Ab*（k）。

5）對抗體種群Ab*（k）中的抗體執行修復操作，得到新抗體種群Ab'*（k）。

6）根據式（2）計算所有抗體的親和度。

7）對抗體種群Ab（k）和Ab'*（k）執行克隆選擇操作，得到新抗體種群Ab（k+1）。

8）令T=T+1，若滿足終止條件，算法停止，將抗體種群中最優的抗體解碼為線狀要素圖形簡化方案；否則，返回步驟2）。

該算法中主要算子操作如下:

（1）克隆操作

克隆倍數決定算法的局部搜索能力及計算量。為獲得較好的圖形簡化效果，簡化方案對應抗體的親和度越高則抗體被復制的倍數應越大。其中，抗體被克隆的倍數可通過式（3）計算得到［7］

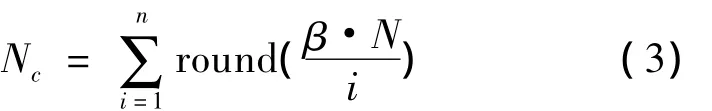
式中，Nc為抗體被克隆的倍數；β為增值系數，由用戶預設；N為種群規模；round（）為取整數操作。如N=10，β=1，則親和力最高的抗體（i=1）將被克隆10倍，親和度次高的抗體將被克隆5倍。

（2）高頻變異

變異是免疫遺傳算法中抗體親和度成熟和抗體多樣性產生的主要手段，決定著算法的全局搜索能力，變異概率決定算法收斂性能。本算法中抗體的變異是將抗體上某個基因位的值取反的過程，如圖1所示。在進行變異操作時，各抗體上的基因值均按照一定的概率Pm隨機確定該基因位是否進行變異。

圖1 抗體變異原理

（3）交叉操作

交叉是免疫遺傳算法保持種群進化過程中抗體多樣性的輔助方式，決定算法的局部搜索能力。常用的交叉方式有單點交叉、兩點交叉和均勻交叉。本算法采用單點交叉方式，即將2個被選中抗體的基因鏈按照一定概率Pc進行交叉，生成2個新的子抗體，交叉位置是隨機的（如圖2所示）。

圖2 抗體交叉原理

（4）不可行解的修復

不可行解修復機制的引入是為了保證線狀要素圖形簡化過程中的幾何精度，其本質是將抗體解碼為線狀要素圖形簡化方案，以判斷線狀要素上各節點的保留及舍棄是否合理。具體操作步驟如下［6］:

1）判斷節點的舍棄是否合理。沿線狀要素方向依次取2個相鄰的保留節點，若該兩節點間存在已被舍棄的點，則尋找出與此兩節點連線距離最遠的節點，計算該距離。若該距離小于指定的距離限差，則說明此兩節點間其他節點的舍棄均合理。繼續搜索判斷節點舍棄的合理性，若搜索至最后一個節點則轉到步驟2），否則繼續轉到步驟1）執行；若該距離大于指定距離限差，說明搜索到的節點為不應舍棄的點，將該點的抗體基因位的值由0變成1，繼續轉到步驟1）執行。

2）判斷線狀要素上各保留節點的選取是否恰當。沿線的方向依次取3個相鄰保留節點，計算中間節點到前后兩相鄰保留節點連線的垂直距離。若該距離小于指定距離限差，則說明該節點是應舍棄的點，將其抗體上該節點基因位上的值由1變為0，繼續轉到步驟1）執行；若該距離大于指定距離限差，說明該節點的保留是恰當的。

三、試驗與分析

1.試驗數據

本文采用的試驗數據為某縣級境界線的部分數據，原始線狀要素如圖3所示，線上有726個節點。本文將用不同的算法以不同的距離限差作為線狀要素數據壓縮的條件進行試驗。

圖3 原始線狀要素

2.試驗結果分析

試驗采用的距離精度限差為1～3 m。當距離為1 m時，設置免疫遺傳算法的種群規模為100，增值系數為0.08，變異率為0.01，交叉率為0.002，運行代數為200代。圖4是距離限差為1 m時免疫遺傳算法、免疫算法、遺傳算法和道格拉斯算法4種算法簡化后的圖形；圖5是算法收斂曲線。各算法在不同距離限差條件下簡化結果指標值見表1。

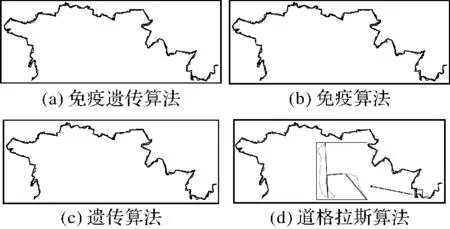
圖4 距離限差為1 m的圖形簡化結果

由試驗結果可得到以下結論:

1）圖形上。4種算法的簡化結果均能較好地保持線狀要素的形狀。道格拉斯算法在保持極值點方面表現較好；智能優化算法在保持對線狀要素形狀保持貢獻更大的點方面表現更佳，簡化后的圖形效果更好；免疫遺傳算法和單純免疫算法的簡化結果一致，優于遺傳算法的簡化結果。

2）優化算法效率。從算法收斂圖看，當距離限差為1時，免疫遺傳算法在運行118代后找到最優解；免疫算法運行185代后解達到最優；遺傳算運行200代仍未找到最優解。免疫遺傳算法的收斂速度明顯快于單純的免疫算法和遺傳算法，算法效率更高。

3）綜合指標。從表1可看出，免疫遺傳算法相對其他3種算法，在表示節點數相近的情況下，總的節點貢獻值最大，親和度函數值最大，算法保留了對圖形形狀貢獻較大的點。免疫遺傳算法在平衡保持線狀要素圖形特征點、減少保留節點數量和幾何精度控制上表現更佳。

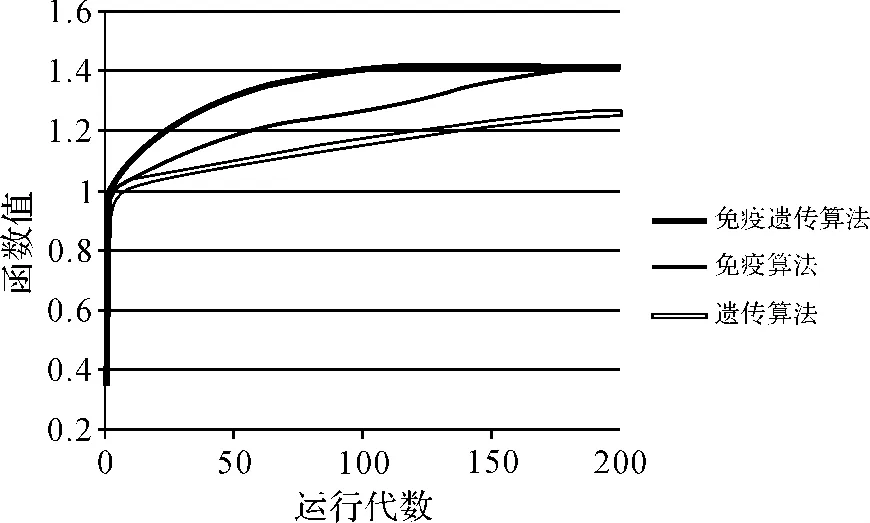
圖5 算法收斂曲線圖

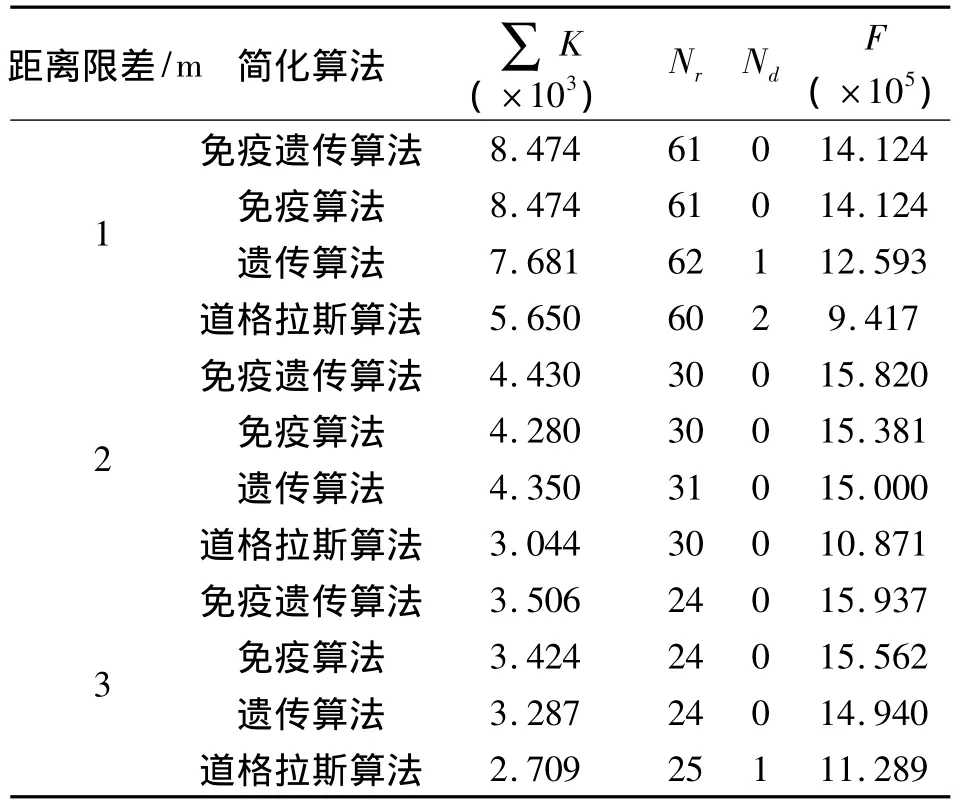
表1 不同距離限差下各算法的線狀要素圖形簡化指標對比

四、結束語

本文顧及線狀要素的幾何精度和圖形特征點，并結合不可行解修復機制，提出一種基于免疫遺傳算法的線狀要素圖形簡化方法，在線狀要素圖形形狀特征的保持方面取得良好的效果，為智能算法應用于地圖綜合領域提供了一定的理論和實踐基礎。研究成果也能為地圖生產提供相應的理論指導和技術支持。同時，線狀要素簡化過程中隨著比例尺的縮小可能產生的空間沖突、地理信息語義不一等問題的處理仍有待作進一步研究。

［1］ DOUGLAS D，PEUCKER T.Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature［J］.The Canadian Cartographer，1973，10（2）:112-122.

［2］ LI Z L，OPENSHAW S.Algorithms for Antomated Line Generalization Based on a Natural Principle of Objective Generation［J］.INT.J.Geographical Information Systems，1992，6（5）:373-389.

［3］ CROMLEY R G，GAMPBELL G M.Integrating Quantitative and Qualitative Aspects of Digital Line Simplification［J］.The Cartographic Journal，1992，29（1）:25-30.

［4］ 郭慶勝.線狀要素圖形綜合的漸進方法研究［J］.武漢大學學報:信息科學版，1998，23（1）:54-58.

［5］ 武芳，鄧紅艷.基于遺傳算法的線要素自動化簡模型［J］.測繪學報，2003，32（4）:349-355.

［6］ 鄭春燕，郭慶勝，胡華科.基于蟻群優化算法的線狀目標簡化模型［J］.測繪學報，2011，40（5）:635-638.

［7］ 梁勤歐.人工免疫系統與GIS空間分析應用［M］.武漢:武漢大學出版社，2011.

［8］ DE CASTRO L N，VONZUBEN F J.Artificial Immune System:Part I——Basic Theory and Applications［M］.Campinas，SP:State University of Campinas，1999.

［9］ 郭慶勝，黃遠林，鄭春燕，等.空間推理與漸進式地圖綜合［M］.武漢:武漢大學出版社，2007.

［10］ FREKSA C，BRAUER W，HABEL C，et al.Spatial Cognition II:Integrating Abstract Theories，Empirical Studies，Formal Methods，and Practical Application［M］.Berlin:Springer，2000.