方位大失準角的捷聯慣導非線性快速對準研究

熊 劍，魏林生，郭 杭，劉 蓉

(1.南昌大學裝備與測控教研室，江西南昌330031;2.南昌大學空間科學與技術研究院，江西南昌330031;3.南京航空航天大學，江蘇南京210016)

一、引 言

慣性導航在航空、航海、礦山、測繪等領域得到了廣泛應用［1］。初始對準是慣性導航中的一項關鍵技術，其主要目的是獲得載體系相對導航系的姿態位置關系，是慣性導航系統工作的前提條件。捷聯慣性導航系統的典型對準方法是解析粗對準，其基本原理是利用慣性器件測量重力加速度和地球自轉角速度，從而計算出捷聯慣導初始姿態矩陣。當三軸失準角都處于小角度范圍時，可再通過建立捷聯慣導線性誤差模型，并利用線性卡爾曼濾波進一步進行捷聯慣導的精對準［2-3］。

出于提高對準速度的考慮，需要在大失準角情況下就進行精對準，上述的線性假設條件不能滿足。考慮到水平對準精度較高、速度較快，可對水平失準角進行簡單計算后便進入精對準，此時水平失準角一般能夠滿足小角度假設條件，但是方位失準角仍為大角度，這種情況下仍需要建立捷聯慣導初始對準的非線性誤差方程，采用非線性濾波進行初始對準［4-6］。UKF(unscented Kalman filter)非線性濾波方法基于UT(unscented transformation)變換理論，其濾波精度較高，可作為方位大失準角初始對準的優選方案［7-8］。

本文建立了方位大失準角非線性初始對準濾波模型，分析了基于UT非線性變換的UKF算法原理，推導了方位大失準角情況下增加陀螺信息輔助方位對準的方法，提出了基于UKF非線性濾波方法的方位大失準角非線性快速初始對準方案;最后，通過計算機仿真并驗證了方位大失準角非線性快速對準方案的有效性。

二、方位大失準角非線性對準建模

針對方位大失準角初始對準問題進行如下假設：當地地理位置精確已知，忽略位置誤差和重力計算誤差;不考慮垂直通道的耦合影響;忽略哥氏加速度的影響;將加速度計誤差模型近似為常值零偏εb+白噪聲wg，陀螺誤差模型近似為常值漂移 Δa+白噪聲wa。初始對準的導航坐標系為東—北—天地理坐標系。捷聯慣導系統的初始狀態設置為

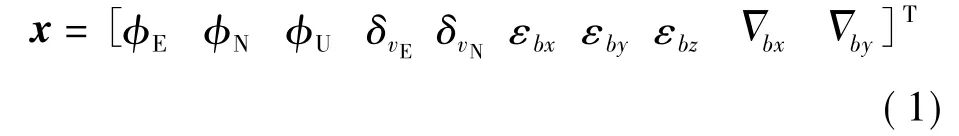
式中，δvE為東向速度誤差;δvN為北向速度誤差;φE、φN、φU為3個失準角。

則初始對準系統模型［9-10］為

式中，G為噪聲系數矩陣。非線性向量函數為

f(x)=

取兩個水平速度為觀測量，則觀測方程如下

三、采用UT非線性變換的UKF原理

1.UT非線性變換

Julier等人基于UT非線性變換提出了UKF方法，并用于處理非線性狀態估計問題。其核心思想是近似概率分布比近似函數精度更高。假設非線性變換y=f(x)，利用UT變換可以得到2n+1個sigma點χi，利用sigma點和權值可求解變量y的統計特性，相應公式如下

y的統計特性可以根據以下公式計算

2.UKF非線性濾波算法

通過UT變換可以比EKF更為準確地求出隨機變量非線性變換后的統計特性，結合Kalman濾波遞推框架，可以得到UKF非線性濾波器［7-8］。假設非線性系統為加性噪聲的情況，設非線性系統為

式中，xk為k時刻系統的n維狀態向量;uk為外部輸入;yk為m維量測向量;vk為系統過程噪聲，且vk～N( 0 ，Rv);nk為量測噪聲，且 nk～ Ν (0 ，Rn)。則UKF濾波流程如下：

1)時間更新過程

2)量測更新過程

四、基于UKF非線性濾波的快速對準方法

1.基于UKF的方位大失準角對準方案

相對擴展卡爾曼濾波(extended Kalman filter，EKF)和粒子濾波(particle filter，PF)，UKF具以下特點：精度高于EKF方法，略低于PF;計算量略大于EKF，但遠遠低于PF。對于方位大失準角的初始對準問題，系統非線性特性略為突出，系統噪聲特性可以用高斯白噪聲得到較好的近似，因此選用UKF非線性濾波方法構成系統初始對準濾波器，如圖1所示。

圖1 基于UKF的方位大失準角非線性快速對準方案

較多的文獻分析并對比了不同非線性濾波算法用于大失準角初始對準的效果，各種非線性濾波算法在方位失準角上的收斂速度表現略有差異。方位失準角收斂速度低的主要原因在于初始對準系統的不完全可觀，期望通過采用不同濾波器提高初始對準速度，實際上難以獲得實質上的改觀。如圖1所示，本文在UKF非線性濾波方法的基礎上，增加陀螺信息作為新的觀測量，并通過陀螺信息輔助方位對準，來提高方位失準角的對準速度。

2.增加陀螺信息的方位大失準角觀測方程推導

水平失準角φE、φN為小角度，方位失準角為大角度時，有：cosφE≈1，sin φE≈φE，cosφN≈1，sinφN≈φN。n系通過3次轉動可以得到c系［9］

則n系到c系的方向余弦矩陣如下

等效陀螺的常值漂移可以表示為

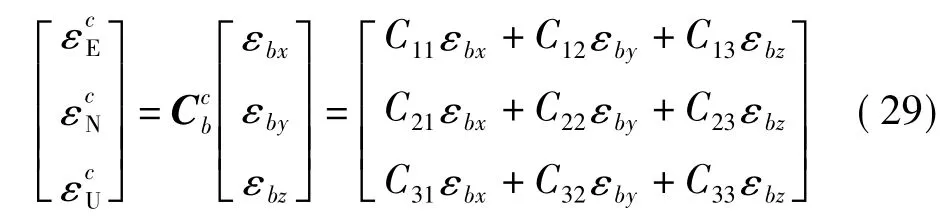
則方位大失準角情況下等效東向陀螺輸出為

取兩個水平速度為觀測量，并增加等效東向陀螺輸出作為新的觀測量，則觀測方程列寫如下

利用式(31)和式(3)可構成增加陀螺信息輔助方位對準的準非線性濾波模型，在此基礎上利用UKF非線性濾波方法，可實現方位大失準角情況下的捷聯慣導非線性快速對準。

五、仿真與分析

對基于UKF的方位大失準角非線性快速對準方案進行仿真，以驗證方案的可行性和對準效果。仿真中陀螺等效精度為0.01°/h，加速度計零偏1 ×10－4g，為便于比較兩種方案的對準效果，慣性器件隨機常值誤差設定為定值：陀螺隨機常值取0.01°/h，加速度計隨機常值取 1 ×10－4g。初始姿態角為0°、0°、90°(橫滾、俯仰和航向)。初始位置為115.9°、28.68°、500 m(經度、緯度和高度)。仿真步長1 s，時間1000 s。

仿真中水平失準角均設置為1°，為了觀察不同方位失準角情況下的對準效果，方位失準角初值分別設成 1°、10°、20°和 30°進行仿真(分別稱為條件1、2、3和4)。將本文方案與常規UKF濾波進行對比，并在不同方位失準角情況下進行驗證，結果如圖2～圖7所示，其中虛線代表采用常規UKF濾波方案的仿真結果，實線為本文所提出方案的仿真結果。

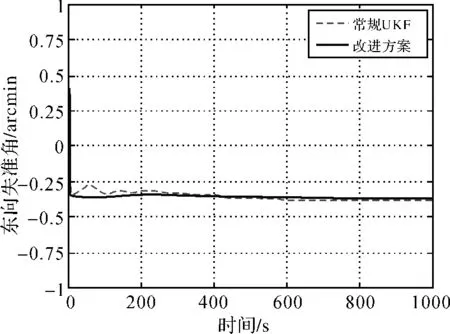
圖2 條件1下東向失準角

圖3 條件1下北向失準角

圖4 條件1下方位失準角

圖5 條件2下方位失準角

圖6 條件3下方位失準角

圖7 條件4下方位失準角

圖2～圖3為條件1下兩種不同對準方案的水平姿態角誤差。由于水平失準角的可觀測性很高，因此水平姿態角在兩種方案中均能快速收斂，其中采用常規UKF方案的水平姿態角誤差略有些震蕩，但兩種方案的水平姿態角對準精度基本是類似的。其他條件下水平姿態角的收斂情況與條件1也基本是類似的，因此本文不再給出相應的仿真結果。

圖4～圖7分別是在條件1～條件4四種情況下方位角對準的仿真結果。從圖中可以看出，在4種條件下改進方案的方位角都能以較高的速度收斂，隨著失準角的增大，收斂時間略有增加。圖中虛線代表采用常規UKF濾波方案的仿真結果，其方位角的收斂速度明顯低于改進方案，其收斂時間均為300 s左右。雖然，兩種方案中方位角的最終對準精度都是類似的，但是常規UKF方案中方位角收斂過程波動較大，其對準的性能綜合評價要低于改進方案，尤其是在對準速度上，改進方案有著明顯的優勢。

六、結束語

本文基于UKF非線性濾波方法，分析和推導了方位大失準角的非線性對準模型，并在此基礎上提出了基于UKF的方位大失準角非線性快速對準方案，該方案增加陀螺信息作為新的觀測量，在保證對準精度的前提下，有效地提高了捷聯慣導方位大失準角情況下初始對準的快速性。

［1］石震，楊志強，田永瑞，等.基于高精度基準數據網的陀螺全站儀尋北精度及穩定性評價方法［J］.測繪通報，2012(1)：91-94.

［2］ZHANG CB，TIAN WF，JIN Z H.A Novel Method Improving the Alignment Accuracy of a Strapdown Inertial Navigation System on a Stationary Base［J］.Measurement Science and Technology，2004，15(4)：765-769.

［3］WANG X L，SHEN G X.A Fast and Accurate Initial Alignment Method for Strapdown Inertial Navigation System on Stationary Base［J］.Journal of Control Theory and Applications，2005，3(2)：145-149.

［4］LI X，YU L，BAO K S，XIAO X J.A Novel Nonlinear Filter for Initial Alignment in Strapdown Inertial Navigation System［C］∥2nd International Symposium on Systems and Control in Aerospace and Astronautics.Shenzhen：ISSCAA，2008：1-6.

［5］HAN SL，WANGJL.A Novel Initial Alignment Method for GPS/INSIntegration with Large Initial Heading Error［C］∥22nd International Technical Meeting of the Satellite Division of the Institute of Navigation 2009，ION GNSS 2009.Savannah， Georgia：［s. n.］，2009：2832-2842.

［6］ZHAO L，NIE Q，GAO W.A Comparison of Nonlinear Filtering Approaches for In-motion Alignment of SINS［C］∥Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation.Harbin：IEEE，2007：1310-1315.

［7］張衛明，張繼惟，范子杰，等.UKF方法在慣性導航系統初始對準中的應用研究［J］.系統工程與電子技術，2007，29(4)：589-592.

［8］EUN H S，NASER E S.An Unscented Kalman Filter for In-motion Alignment of Low-cost IMUs［C］∥Position Location and Navigation Symposium，2004.［S.l.］：IEEE，2004：273-279.

［9］李東明.捷聯式慣導系統初始對準方法研究［D］.哈爾濱：哈爾濱工程大學，2006.

［10］馬建軍，鄭志強.基于插值非線性濾波的SINS靜基座初始對準［J］.系統仿真學報，2007，19(12)：2783-2789.