飽和地基表面基礎在Rayleigh 波 作用下的搖擺振動分析

王 鵬，王 軍，蔡袁強, ，丁光亞

（1.溫州大學 建筑與土木工程學院，浙江 溫州 325035；2.浙江大學 建筑工程學院，杭州 310058）

1 引 言

基礎對激震波的散射以及由此造成的地基與基礎的耦合振動研究一直是土動力學和地震工程中的重要課題，前人對此做了許多卓有成效的研究[1－5]。但以往大部分研究都把土體模擬成彈性介質，而由于地下水的存在，把土體模擬成兩相介質更為合理。同時由于Rayleigh 波傳播所攜帶的能量要比縱波（P 波）及剪切波（SV 波）大得多，且幾何衰減又慢，Rayleigh 波已被認為是危害較大的地震波。在建筑施工、交通車輛及機器運行所產生的振動波中，Rayleigh 波也是占主要形式的波種。因此，對Rayleigh 波作用下基礎的振動特性進行研究顯得尤為必要。

在彈性波動理論的基礎上，眾多學者對飽和土中Rayleigh 波的各種特性進行了比較詳盡的研究。Tajuddin[6]建立了考慮2種壓縮波的Rayleigh波特征方程。夏唐代等[7－8]通過對飽和土中波的運動方程及連續方程分析，推導了飽和半空間土層中Rayleigh波彌散特征方程，并由此討論了Rayleigh 波的彌散特性及位移、孔壓分布情況。劉凱欣等[9]基于Biot理論研究了橫觀各向同性飽和多孔介質中Rayleigh波的傳播特性，導出了廣義Rayleigh 波的三維復合方程，給出了Rayleigh 波的存在條件。在Rayleigh波導致的飽和土與結構相互作用方面，陸建飛等[10]利用Muki 的虛擬樁方法，研究了頻域內半空間飽和土中單樁在Rayleigh 波下的動力響應。Cai 等[11]對飽和半空間中非連續屏障對Rayleigh 波的隔振效果進行了研究。

基于Biot 波動理論，本文采用半解析的方法對飽和地基表面剛性圓形基礎在Rayleigh 波作用下的搖擺振動問題進行了研究。首先引入勢函數求解土體控制方程，得到飽和土體中的Rayleigh 波場并視其為自由波場，隨后采用Hankel 變換求解土體控制方程得到土體應力-位移表達式。為考慮基礎對Rayleigh 波的散射以及地基與基礎的動力相互作用，將土體中的散射波場定義為輻射散射波場及剛體散射波場的疊加。結合基礎搖擺振動的混合邊值條件及基礎的動力平衡方程，最終得到基礎的搖擺振動位移幅值表達式，并對相關參數進行了分析。

2 基本動力方程

分析模型如圖1 所示，半徑為 r0的圓形基礎位于飽和地基表面并受Rayleigh 波的作用，坐標系原點 O1位于基礎下表面中心點處。假定地基為飽和半空間，由均質彈性飽和多孔兩相介質組成，基礎為有質量的剛性圓盤，基底與地基之間緊密接觸，接觸面光滑且相互之間無滑移。同時假定所有的運動形式皆為簡諧運動，則各運動形式可表示為時間t的函數，即 f (t ) = f eiωt，為簡略起見，下文中省去因子

eiωt。

圖1 分析模型及坐標系統 Fig.1 Analytical model and coordinate system

2.1 飽和土體中的Rayleigh 波

根據Biot 波動理論[12－13]，飽和土體的基本運動方程為

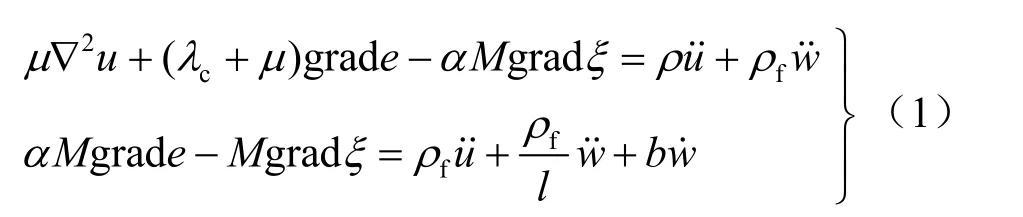
引入標量勢sφ 、fφ 和矢量勢sψ 、fψ ，將位移場場作如下分解：

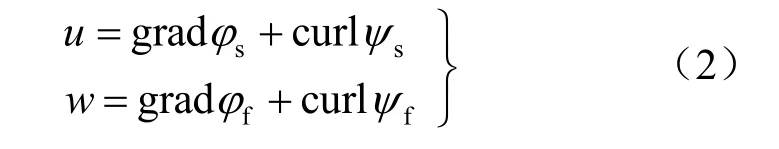
式中：下標s、f 分別表示固體部分和流體部分。

將式（2）代入式（1），可得到半空間飽Rayleigh波的勢函數

式中：1A 、2A 、3A 為常數； /k cω= 為Rayleigh波波數，c 為Rayleigh 波相速度，ω 為角頻率；1a=， a2= 1-， a3= 1-，vp1、vp2為壓縮波波速；sv 為剪切波波速；1γ 、2γ 、3γ 為飽和土中液相與固相勢函數的比值。p1v 、p2v 、sv 、1γ 、2γ 、3γ 具體取值見文獻[11]。

飽和土應力與勢函數關系為

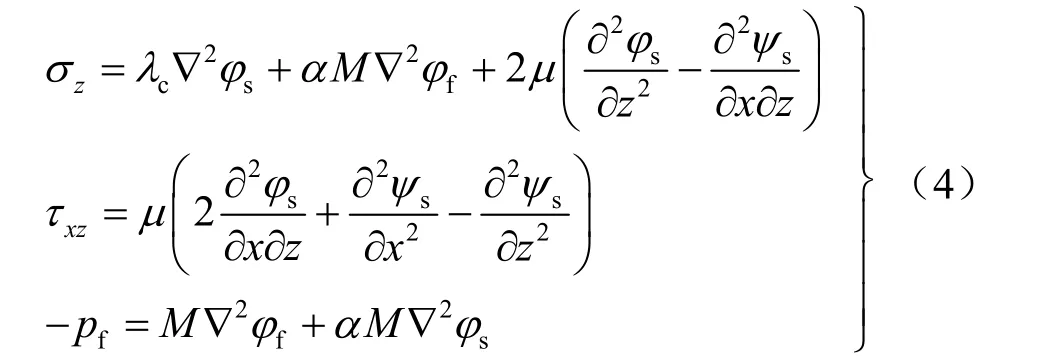
式中：zσ 、xzτ 為土骨架應力；fp 為孔隙水壓力。

若假設飽和地基表面透水，則在 0z= 處：

若飽和地基表面不透水，則在 0z= 處：

式（3）結合邊界條件式（5）、（6），可得到不同透水條件下Rayleigh 波波速的解，進而可得到飽和地基中Rayleigh 波勢函數的表達式。

2.2 飽和土體控制方程求解

在圓柱坐標系下，式（1）可表示為

飽和土應力-應變關系為

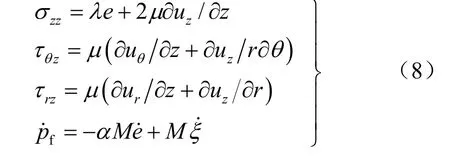
為考慮θ 的影響，將所有位移及應力對θ 進行如下形式的Fourier 展開：

引入以下無量綱參數： ω0=、 λ*=

并定義位移由0r 無量綱化，應力由μ 無量綱化。

利用Hankel 變換并結合式（8）、（9），按蔡袁強等[15]運用的方法對式（7）進行求解：

式中：上標n 表示對函數進行n 階Hankel 變換，下標n 表示對θ 進行Fourier 展開后的第n 階函數；A1n、 A2n、 A3n為包含ε 的待定系數。變量 q1、 q2、

3q 、21c 、22c 、31c 、32c 、41c 、42c 、43c 、51c 、52c的取值為

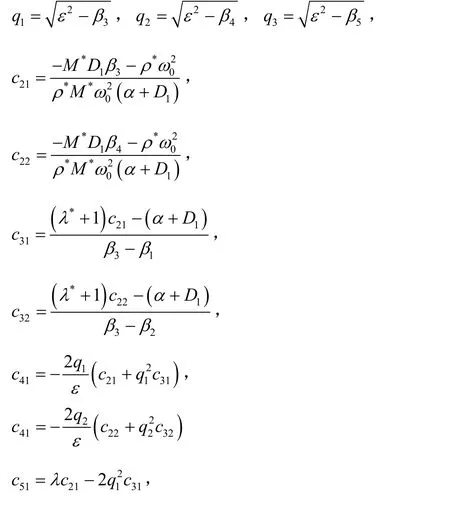
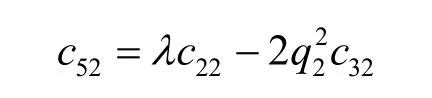
其中

在此，參數 q1、q2、滿足 Re( q1) ＞ 0，R e( q2) ＞ 0，Re( q3) ＞ 0。

3 邊界條件及求解

飽和地基中剛性基礎的搖擺振動研究屬于混合邊值問題，即在基底給定位移，在基底外給定應力。無量綱化后*0z = 處的邊界條件為

當地基表面透水時：

當地基表面不透水時：

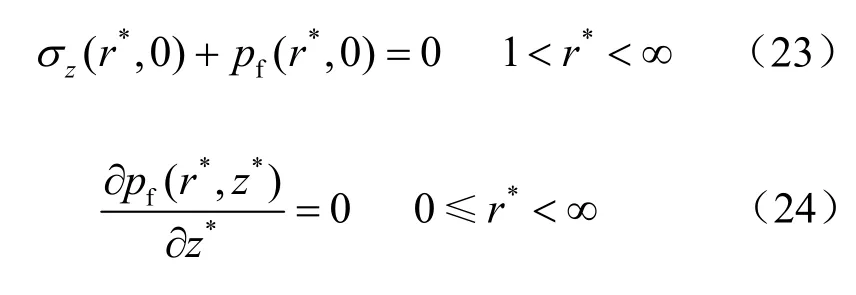
定義入射Rayleigh 波場為飽和半空間中的自由波場，描述了其在飽和半空間中的傳播特性，用 ufree表示。由于飽和半空間表面剛性基礎的存在，Rayleigh 波會發生散射，此時可將剛性基礎看作一個次生波源。根據Pao 等[16]所提出的彈性波散射理論，土體中的散射波場可劃分為2 部分，一部分為剛體散射波場 uS，一部分為輻射散射波場 uR。前者為入射波在傳播過程中遇到固定的剛性基礎時產生的散射波，表示基礎在自由波場與剛體散射波場的共同作用下，位移為0；后者為剛性基礎在振動過程中產生的波輻射，其中包含了基礎尚屬未知的振動幅值。根據以上定義，此時飽和土體中的全波場可定義為 Utot= ufree+ uS+ uR。

根據土體中波場的劃分，當飽和地基表面透水時，式（18）、（21）可轉化為

而當地基表面不透水時，

當Rayleigh 波入射時，自由波場引起的無量綱豎向位移為[11]

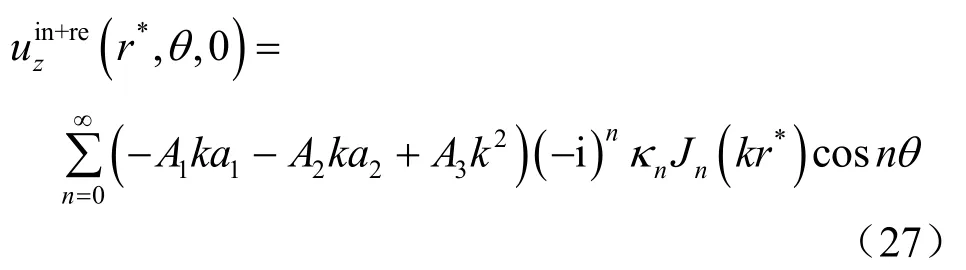
式中：n=0 時 κn= 1； n ≠ 0時 κn= 2。

根據式（11）～（26）并結合三角函數的正交性，可得到2 組描述Rayleigh 波激勵下基礎搖擺振動的對偶積分方程

不透水條件下，

根據Nobel[17]提出的方法，將式（28）、（29）化為第2 類Fredholm 積分方程

式中： ( , )K x y 為核函數

作用在基底的力矩可由式（30）、（31）求得

式中： T*= T為力矩的無量綱形式。

定義

式中：0η 為輸入位移，對應于入射Rayleigh 波作用下無質量剛性圓形基礎的搖擺振動振幅。

根據式（33），并結合基礎的動力平衡方程可得

式中： m*為基礎無量綱質量， m*= m。

根據振動分析方法[18]，基礎的搖擺位移幅值為

其中，

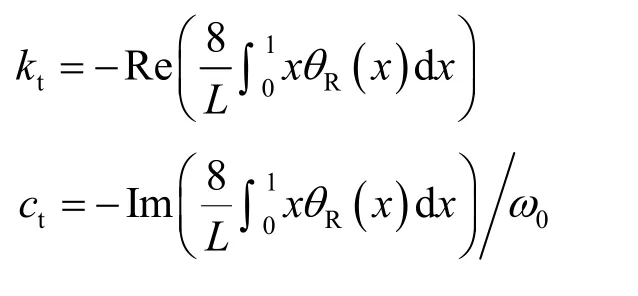
4 算例分析

如圖2 所示，將飽和土體反映流體特性的參數取為極小值（a、 M*、 ρ*及 b*取為 10-5），從而把飽和地基模型退化到單相彈性介質的情況，計算了無質量圓形基礎在Rayleigh 波作用下的搖擺位移振動幅值η0，并與Luco 等[19]的結果進行對比。按照Luco[19]的定義，U0為飽和半空間表面自由波場引起的土體豎向位移。可見本文結果與Luco 的結果能夠較好地吻合，從而驗證了本文方法的正確性。

圖2 本文計算結果和Luco 的結果對比 Fig.2 Comparison between present work and Luco’s work

在此假設入射Rayleigh 波振幅為單位振幅，利用數值結果討論了一些關鍵性參數對基礎搖擺振動特性的影響，飽和土體參數取自文獻[11]，無量綱化后為：α=1，λ*=1.004，M*=246.78，ρ*=0.45，n=0.37，v=0.1～0.4， b*=1～100。

圖3 研究了基礎搖擺振動位移幅值隨入射波頻率的變化，并給出了土體泊松比對搖擺位移幅值的影響。由圖中可以看出，隨著激振頻率的增加，基礎搖擺位移由0 開始增加，達到峰值后減小，位移曲線存在明顯共振現象。

隨著泊松比的增加，基礎的共振振幅明顯增大，共振頻率也略有增加。在0ω 小于共振頻率情況下，0ω＜0.4，不同泊松比下基礎的搖擺振動位移曲線基本重合。

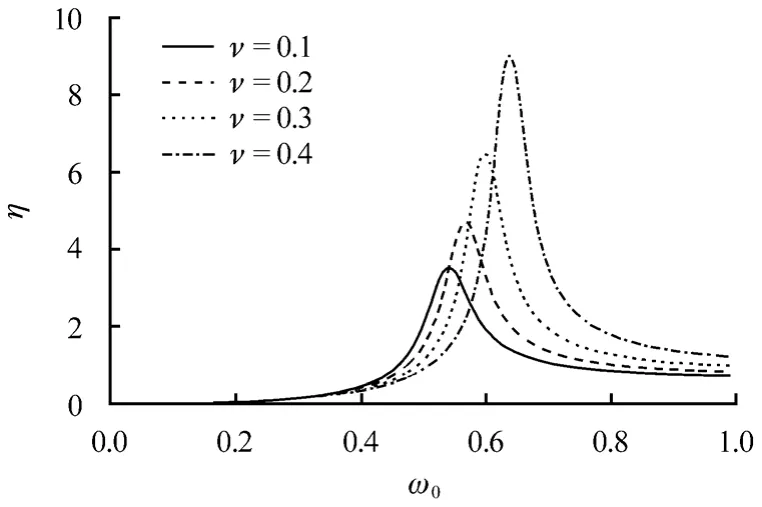
圖3 不同ν 值時η 隨ω0 變化 Fig.3 η versus ω0 under different values of ν

圖4 研究了基礎質量對基礎搖擺振動的影響。圖4 表明，基礎質量的減小將導致基礎共振頻率及共振振幅的明顯增大。由式（36）可以得知，在其他參數一定的情況下，基礎質量的變化僅對共振頻率產生影響。由于基礎質量的減小導致基礎共振點處頻率的增大，入射波頻率的增加造成了基礎底部作用力矩的增長，最終導致基礎共振振幅的增大。

圖4 不同m*值時η 隨ω0 變化 Fig.4 η versus ω0 under different values of m*

在飽和土體中，b*為反映土骨架與孔隙水黏性耦合的系數，隨著 b*增大，土體滲透性逐漸降低。圖5 反映了土體滲透性對基礎搖擺振動的影響。同時將飽和土體反映流體特性的參數取為極小值（a、M*、 ρ*、 b*取為 10-5），把飽和兩相介質退化到單相彈性介質的情況，而其他參數保持不變，將計算結果與飽和介質的振動情況進行對比。如圖所示，由于飽和土體中孔隙水的作用，與單相彈性介質中搖擺振動相比，飽和地基中基礎的搖擺振動共振振幅有所減小。同時隨著土體滲透性的減小（ b*= 100），基礎共振振幅明顯減小，共振頻率略有增加。但也可以發現，對于滲透性較小的土體，基礎位移曲線的衰減要慢。當入射頻率大于共振頻率時，如ω0＞0.7 時，隨 b*的增加，土體中基礎的搖擺位移增大。

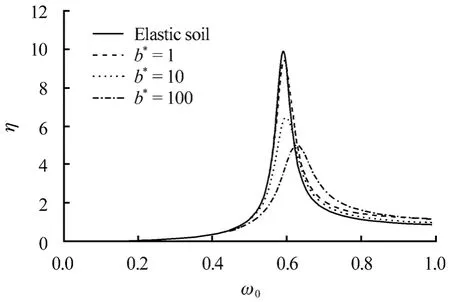
圖5 不同b*值時η 隨ω0 變化 Fig.5 η versus ω0 under different values of b*

圖6 反映了Rayleigh 波作用下飽和地基表面透水條件對基礎振動的影響。相比于透水邊界的情況，當地基表面不透水時，基礎的共振振幅有所減小。其原因在于不透水條件下，飽和地基中土骨架及孔隙水的相互作用更為強烈，激振波能量耗散，從而導致基礎的搖擺振動減弱。

圖6 不同透水條件下η 隨ω0 變化 Fig.6 η versus ω0 under different drainage conditions

5 結 論

（1）無論其他參數如何取值，隨頻率的變化，基礎搖擺振動存在共振現象。泊松比的增加或者基礎質量的減小都將導致基礎共振頻率及共振振幅的增大。

（2）由于孔隙水的影響，飽和土中基礎位移要小于彈性介質中的情況，隨著土體滲透性減小，基礎共振振幅隨之減小，但位移曲線衰減減弱。

（3）由于水-土相互作用的影響，相比于不透水邊界，透水邊界下的基礎搖擺振動更加劇烈。

[1] FLITMAN L M. On the motion of a rigid strip-mass lying on an elastic half space and excited by a seismic wave[J]. Journal of Applied Mathematics and Mechanics, 1962, 26: 1582－1604.

[2] KARASUDHI P, KEER L M, LEE S L. Vibratory motion of a body on an elastic half space[J]. Journal of Applied Mechanics, 1968, 35: 679－705.

[3] THAU S A. Radiation and scattering from a rigid inclusion in an elastic medium[J]. Journal of Applied Mechanics, 1967, 34(2): 509－511.

[4] THAU S A, UMEK A. Transient response of a buried foundation to antiplane shear waves[J]. Journal of Applied Mechanics, 1973, 40(4): 1061－1066.

[5] 李偉華, 趙成剛, 杜楠馨. 軟弱飽和土夾層對地鐵車站地震響應的影響分析[J]. 巖土力學, 2010, 12(31): 3958－3963. LI Wei-hua, ZHAO Cheng-gang, DU Nan-xin. Analysis of effects of saturated soft interlayer on seismic responses of metro station[J]. Rock and Soil Mechanics, 2010, 122(31): 3958－3963.

[6] TAJUDDIN M. Rayleigh wave in a poroelastic half- space[J]. Journal of the Acoustical Society of America, 1984,75(3): 682－684.

[7] 夏唐代, 陳龍珠, 吳世明. 半空間飽和土中瑞利波特性[J]. 水利學報, 1998, 2(2): 47－53. XIA Tang-dai, CHEN Long-zhu, WU Shi-Ming. Charac- teristics of Rayleigh waves in a saturated half-space soil[J]. Journal of Hydraulic Engineering, 1998, 2(2): 47－53.

[8] 夏唐代, 顏可珍, 孫鳴宇. 飽和土層中瑞利波的傳播特性[J]. 水利學報, 2004, 11(11): 81－84. XIA Tang-dai, YAN Ke-zhen, SUN Ming-yu. Propagation of Rayleigh wave in saturated soil layer[J]. Journal of Hydraulic Engineering, 2004, 11(11): 81－84.

[9] 劉凱欣, 劉穎. 橫觀各向同性含液飽和多孔介質中瑞利波的特性分析[J]. 力學學報, 2003, 35(1): 101－104. LIU Kai-xin, LIU Ying. Characteristics of Rayleigh waves in transversely isotropic fluid-saturated porous media[J]. Acta Mechanic Sinica, 2003, 35(1): 101－104.

[10] 陸建飛, 聶衛東. 飽和土中單樁在瑞利波作用下的動力響應[J]. 巖土工程學報, 2008, 30(2): 225－231. LU Jian-fei, NIE Wei-dong. Dynamic response of a single pile embedded in half-space saturated soil subjected to Rayleigh waves[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 225－231.

[11] CAI Y Q, DING G Y, XU C J, et al. Vertical amplitude reduction of Rayleigh waves by a row of piles in a poroelastic half-space[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(16): 1799－1821

[12] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ.Low frequency range[J]. Journal of the Acoustial Society of America, 1956, 28(2): 168－178.

[13] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. High frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 179－191.

[14] SNEDDON I. The use of integral transforms[M]. Mcgraw-Hill: New York, 1970.

[15] 蔡袁強, 胡秀青. 飽和地基中埋置剛性圓柱基礎的等效豎向動力剛度[J]. 巖石力學與工程學報, 2008, 27(2): 361－367. CAI Yuan-qiang, HU Xiu-qing. Equivalent vertical dynamic stiffness for embedded rigid cylindrical found- ation in saturated soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 361－367.

[16] MOW C C, PAO Y H. Diffraction of elastic waves and dynamic stress concentrations[M]. New York: [s. n.], 1973.

[17] NOBEL B. The solution of Bessel-function dual integral equations by a multiplying-fact method[J]. Mathematical Proceedings of the Cambrige Philosophical Society, 1963, 59: 351－362.

[18] RICHART F E, HALL J R, WOODS R D. Vibrations of soils and foundations[M]. New York: Prentice-Hall, 1970.

[19] LUCO J E, MITA A. Response of a circular foundation on a uniform half-space to elastic waves[J]. Earthquake Engineering and Structural Dynamics, 1987, 15(1): 105－118.