基于壓縮傳感的混沌自適應控制

趙英寶，黃麗敏

（1.河北科技大學電氣工程學院，河北石家莊 050018；2.河北科技大學現代教育技術中心，河北石家莊 050018）

基于壓縮傳感的混沌自適應控制

趙英寶1，黃麗敏2

（1.河北科技大學電氣工程學院，河北石家莊 050018；2.河北科技大學現代教育技術中心，河北石家莊 050018）

提出了一種自適應混沌控制方法，僅根據輸出時間序列，利用壓縮傳感辨識混沌系統的方程與參數，利用負反饋控制混沌系統到設定目標上。以Lorenz和R?ssler系統為例說明時變結構系統的方程及參數的辨識與控制，首先估計出Lorenz系統方程并將其控制到固定點或周期振蕩上，當系統結構從Lorenz變化到R?ssler時可以快速辨識新結構及其參數，系統重新回到控制目標上。結果表明，與最小二乘法相比，該方法僅通過較少的數據即可實現模型結構與參數的同時估計，并有很高的估計精度，利用估計得到的模型和參數，再利用負反饋可以將混沌系統快速控制到設定目標上。

壓縮傳感；負反饋控制；模型估計；混沌控制；參數估計

動力學研究的正問題，即已知系統動力學方程和參數的情況下研究動力系統的演化或控制，已提出很多研究成果。而在未知方程或參數情況下，由系統輸出時間序列辨識動力學方程和參數，屬于動力學研究的逆問題，辨識系統方程和參數是對系統進行控制的重要前提。對于動力學系統的混沌控制，EDWARD等提出了混沌控制的OGY方法，它是一種不需要知道動力系統方程的控制方法［1］，之后提出了眾多有效的混沌控制方法，從系統方程和參數均已知［2－3］到系統方程已知參數未知［4－5］，均得到了良好的效果。對于未知方程的動力學系統，DITTO等首次將OGY方法應用于未知系統方程的實際物理系統實驗控制［6］；ALSING等利用人工神經網絡［7］、KOBRAVI等利用模糊邏輯方法逼近動力學方程，再執行混沌控制，是一種離線控制方法，其辨識的結果并非動力學方程本身［8］；未知系統方程時，從完全未知的系統中估計方程存在困難，獲知系統方程的先驗知識，即指定系統的統一結構形式，GOUESBET等提出自治多項式結構［9］，BEZRUCHKO等提出非自治微分方程結構，然后利用最小二乘法估計方程和參數［10］，然而這種估計方法收斂速度慢且存在較大穩態誤差。系統結構或參數的改變可能會產生邊界危機等不期望現象，為了解決由輸出時間序列估計系統動力學方程問題，WANG等提出了一種基于壓縮傳感的動力系統模型方程估計方法［11］。筆者基于該方法實現了未知系統方程的辨識及其混沌自適應控制。

利用壓縮傳感估計系統動力學方程，是基于可以將動力學方程表示成多變量冪級數展開形式，且僅有少數項的系數為非零這個基本假設，則模型系數可看成稀疏向量，動力學方程的估計轉化為求解欠定線性系統。DONOHO和CANDèS提出的壓縮傳感方法為求解此類欠定線性方程奠定了基礎［12－13］，并證明了可以利用部分傅里葉系數重建原始信號［14］。由于冪級數系數與結構項的對應關系，利用壓縮傳感求解欠定線性系統可以實現動力學方程和參數的同時估計。壓縮傳感的優點在于信號的投影測量數據量遠小于傳統的采樣方法，突破了香農采樣定理的瓶頸［15］。利用壓縮傳感從含有少量觀測數據中重建源信號，近來在圖像處理［16］、數據通信［17］等領域得到了良好應用。

自適應控制都是已知系統方程而自適應估計系統參數。自適應控制和系統辨識密不可分。筆者提出的基于壓縮傳感的混沌自適應控制方法，首先利用壓縮傳感從觀測時間序列中辨識出未知系統的動力學方程及其參數，再利用負反饋控制方法將其控制到目標點或周期振蕩上。以Lorenz和R?ssler系統為例說明時變結構系統的辨識和控制，該方法實現了Lorenz系統方程和參數的快速辨識并進行混沌控制，當系統在某時刻由Lorenz系統跳變到R?ssler系統時，可以快速辨識出系統新的動力學方程和參數，實現控制混沌系統重新回到設定目標上。本控制策略對于實現時變結構非線性系統的混沌自適應控制非常有意義。

1 壓縮傳感原理

壓縮傳感是一種求解欠定線性系統稀疏解的方法，由于欠定線性系統中未知數的個數大于方程的個數，所以通常會有無窮多個解，但是如果系統有唯一的稀疏解，則人們可以通過壓縮傳感方法，利用較少的觀測量便能重建稀疏解。

壓縮傳感過程可分為信號的稀疏化、構建穩態測量矩陣和利用重建算法恢復源信號3部分。壓縮傳感描述如下：已知某傳感矩陣φ∈RM×N，且N?M，稀疏向量x∈RN×1在矩陣φ下的輸出為y∈RM×1，即y＝φx，壓縮傳感的目的就是根據y重建x。當處理圖像或高維數據時應將其多維向量轉換為一維長向量。若x的時域信號是非稀疏的，可將其進行某種變換使其可以稀疏表示，常用的變換有傅里葉變換、小波變換和冗余字典等。為了重建源稀疏信號，觀測數據量必須滿足O（KlnN），其中K為源稀疏信號非零項的個數，且矩陣φ必須滿足約束等距條件［18］。對于源信號的恢復重建已有多種算法，文獻［14］已證明，利用測量值通過求解最優l1－范數可重構x：

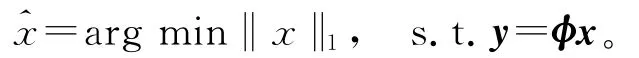
這是一個凸最優問題，可以轉化為線性規劃問題求解，即基追蹤。其他重建算法還有匹配追蹤算法、最小全變分法等。

2 壓縮傳感估計方法

考慮如下n維動力系統：

其中x＝（x1，x2，…，xn）∈Rn為系統狀態變量，p為系統參數。

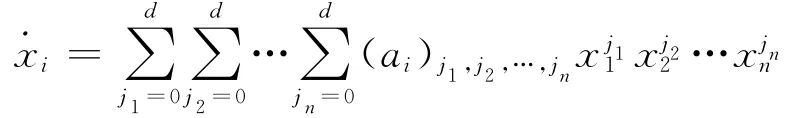
當系統在某參數p下演化時，獲得第i個系統狀態變量μ個測量值（xi（t1），xi（t2），…，xi（tμ）），并根據測量值求得），…，同時求得矩陣φ的μ個行向量?φ（t1），φ（t2），…，φ（tμ），由此獲得如下等式：

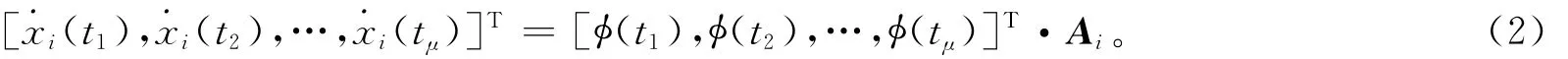
其中Ai為由系數（ai）j1，j2，…，jn組成的列向量，利用壓縮傳感便可以估計出Ai的值，由于Ai與系統各項存在對應關系，便可估計出系統的方程。為了滿足約束等距性，將矩陣φ的每個元素除以該元素所在列的2－范數。

3 模型辨識

Lorenz系統和R?ssler系統為研究非線性系統混沌現象的常用方法，是用于驗證混沌控制方法的常用對象，2個系統描述如下。

Lorenz系統：

當系統參數a＝10，b＝28，c＝8／3時系統處于混沌狀態。

R?ssler系統：

當系統參數d＝0.2，e＝0.2，f＝5.7時系統處于混沌狀態。

對于確定性系統而言，選取的冪指數越大意味著求取的向量越稀疏。以Lorenz系統取冪指數d＝3為例，在ti時刻，

共64項，由式（5）可見，對而言只有x（ti）1y（ti）0z（ti）0，x（ti）0y（ti）1z（ti）0這2項所對應的系數為非零，其余項所對應的系數皆為零；同理只有x（ti）1y（ti）0z（ti）0，x（ti）0y（ti）1z（ti）0，x（ti）1y（ti）0z（ti）1這3項為非零只有x（ti）1y（ti）1z（ti）0，x（ti）0y（ti）0z（ti）1這2項為非零。φ（ti）的系數向量為一稀疏向量，根據壓縮傳感原理，通過μ個的值和φ（t1），φ（t2），…，φ（tμ），可以估計出φ（ti）所對應的系數向量Ai非零系數向量同理可得。

由于未知系統方程形式，定義絕對誤差與相對誤差存在困難，利用估計值在某個滑動窗內波動范圍小于某一小的正實數ε來確定估計是否完成，即第i個系數在某時刻τ滿足

其中，j＞N且j∈｛τ－N＋1，τ－N＋2，…，τ｝，ε為估計精度。

4 負反饋混沌控制

根據測得的時間序列，按前述方法估計出系統的結構和參數，將估計得到的動力學方程按照文獻［3］的控制策略將混沌系統控制到設定目標上。

為了使2個系統都穩定在x＝p1，y＝p2點上，

Lorenz控制輸入取為

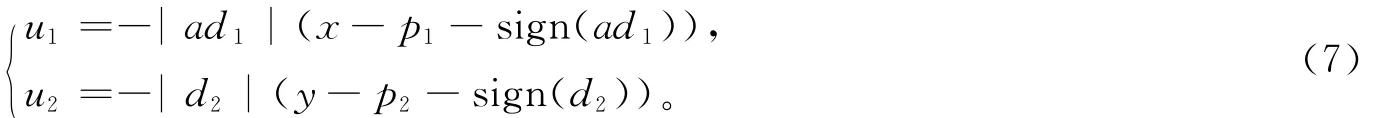
R?ssler控制輸入取為

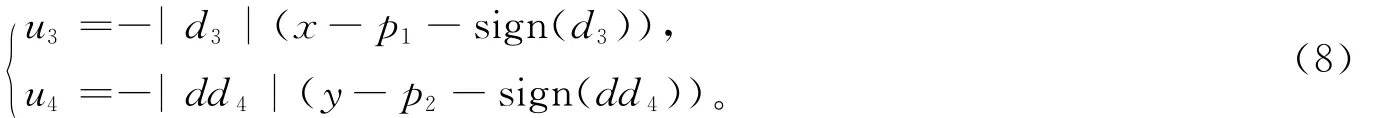
根據穩定性條件＝0，參數d1，d2，d3，d4分別為

為了將系統控制到任意周期軌道上，用一個外部振蕩器產生正弦信號x＝p1＝rsin（ωt），y＝p2＝cos（ωt），代入式（9）、式（10）得到相應控制參數，將式（9）、式（10）代入式（7）、式（8）得到控制輸入。

5 仿真實驗

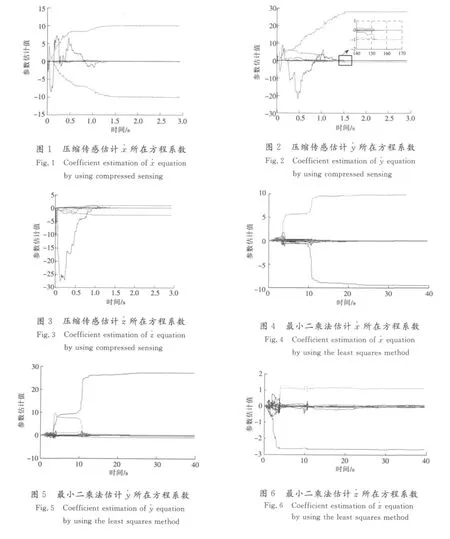
Lorenz系統的結構和參數辨識，取最大冪指數d＝3，共有64個系數，步長為0.01時，系數估計值隨時間序列向量個數的關系如圖1—圖3所示，可以看出，非零項快速收斂到其真實值，零項收斂到零。而利用遞推最小二乘法估計的結果收斂速度很慢且有較大的穩態誤差，如圖4－圖6所示。根據非零系數與非零項的對應關系，便估計出了系統的動力學方程。

取初始值不同，完成辨識的速度也不同。對Lorenz系統而言，當步長取0.01，初始值選擇為x（0）＝2.5，y（0）＝－1.8，z（0）＝0.5時，按式（6）條件需要304個點才能完成估計，相同步長下初始值選擇為x（0）＝0.01，y（0）＝0.03，z（0）＝0.05時，只需207個點就可以完成估計。如果將估計參數按式（6）中ε精度舍入，則估計得到的方程就是Lorenz系統的實際方程。

當取p1＝2.5，p2＝－1時，第20s時施加控制，施加控制后系統變量很快被控制到了固定點上，而當第40s時結構發生了變化，由Lorenz系統變為R?ssler系統，重新啟動系統辨識，經過一段時間后得到了時間序列新的動力學方程。在第60s時再一次施加控制，經過短暫幾秒系統重新回到目標點（x，y）＝（p1，p2）上，如圖7所示。將系統控制到產生周期振蕩上，取r＝5，ω＝3，如圖8所示，也得到了良好的效果。

對于系統結構的辨識其實收斂速度非常快，圖8中從約第19s開始辨識，到第20s時已達辨識精度要求。辨識完成后開始實施控制，第60s只是施加控制的時間，只需不到2s便可辨識出新系統，而并非經過20s才能將系統辨識出來，圖8只是為了顯示更直觀一些。

當系統結構不變而參數發生變化時，如定點控制中，Lorenz系統參數b由28變成100時，控制系統會收斂到另一點上，由于不滿足約束等距性，這時利用壓縮傳感不能估計出系統方程。解決辦法是零控制輸入為零，讓系統回到混沌狀態，重新辨識參數后再施加控制。

6 結 論

主要研究了在未知混沌系統方程下僅通過時間序列控制混沌的方法，將系統方程辨識方法應用于混沌自適應控制的辨識過程中。相比于利用離線逼近方法控制混沌，本方法是一種在線的辨識；相比于無模型混沌控制，本方法是一種“已知”系統模型的混沌控制，可以實現輸出預測，避免邊界危機；相比于最小二乘法估計系統方程和結構，本方法收斂速度很快且幾乎沒有穩態誤差。提出的基于壓縮傳感的混沌自適應控制方法實現了在未知混沌系統方程情況下，首先利用輸出時間序列估計出了Lorenz和R?ssler系統的方程和參數，并使用負反饋控制將混沌系統成功控制在某一固定點或周期振蕩上，系統方程辨識過程和混沌控制過程均有很快的收斂速度。該控制方法在保密通信、生物工程、控制工程等領域有潛在的應用，為混沌控制提供了一個新的思路。

［1］ EDWARD O，GREBOGI C，YORKE J A.Controlling chaos［J］.Physical Review Letters，1990，64（11）：1 196－1 199.

［2］ QU Zhi－lin，HU Gang，MA Ben－kun.Controlling chaos via continuous feedback［J］.Physics Letters A，1993，178（3／4）：265－270.

［3］ 羅曉曙，劉慕仁，方錦清，等.一種基于系統變量的線性和非線性變換實現混沌控制的方法［J］.物理學報（Acta Physica Sinica），2000，49（5）：849－853.

［4］ 關新平，彭海朋，李麗香，等.Lorenz混沌系統的參數辨識與控制［J］.物理學報（Acta Physica Sinica），2001，50（1）：26－29.

［5］ HUANG De－bin.Adaptive－feedback control algorithm［J］.Physical Review E，2006，73：1－8.

［6］ DITTO W L，RAUSEO S N，SPANO M L.Experimental control of chaos［J］.Physical Review Letters，1990，65（26）：3 211－3 214.

［7］ ALSING P M，GAVRIELIDES A，KOVANIS V.Using neural networks for controlling chaos［J］.Physical Review E，1994，49（2）：1 225－1 231.

［8］ KOBRAVI H R，ERFANIAN A.A decentralized adaptive robust method for chaos control［J］.Chaos，2009，19：1－7.

［9］ GOUESBET G，LETELLIER C.Global vector field reconstruction by using a multivariate polynomial L2approximation on nets［J］.Physical Review E，1994，49（6）：4 955－4 972.

［10］ BEZRUCHKO B P，SMIRNOV D A.Constructing nonautonomous differential equations from experimental time series［J］.Physical Review E，2000，63：1－7.

［11］ WANG Wen－xu，YANG Rui，LAI Ying－cheng，et al.Predicting catastrophes in nonlinear dynamical systems by compressive sensing［J］.Physical Review Letters，2011，106：1－4.

［12］ DONOHO D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：1 289－1 306.

［13］ CANDèS E J.Compressive sampling［A］.Proceedings of International Congress of Mathematicians［C］.Madrid：European Mathematical Society Publishing House，2006.1 433－1 452.

［14］ CANDèS E，ROMBERG J，TAO T.Robust uncertainty principles exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52（2）：489－509.

［15］ 李樹濤，魏 丹.壓縮傳感綜述［J］.自動化學報（Acta Automatica Sinica），2009，35（11）：1 369－1 377.

［16］ DUARTE M F，DAVENPORT M A，TAKHAR D，et al.Single－pixel imaging via compressive sampling［J］.IEEE Signal Processing Magazine，2008，25（2）：83－91.

［17］ TAUBOCK G，HLAWATSCH F.A compressed sensing technique for ofdm channel estimation in mobile environments exploiting channel sparsity for reducing pilots［A］.The IEEE International Conference on Acoustics，Speech，and Signal Processing［C］.Las Vegas：IEEE，2008.2 885－2 888.

［18］ CANDèS E，TAO T.Decoding by linear programming［J］.IEEE Transactions on Information Theory，2005，51（12）：4 203－4 215.

［19］ 陳予恕，梁建術.自適應延時反饋控制混沌方法［J］.河北科技大學學報（Journal of Hebei University of Science and Technology），2006，27（4）：267－271.

［20］ 梁建術，李 蘭.一類參數不確定R?ssler系統的自適應反推混沌控制［J］.河北科技大學學報（Journal of Hebei University of Science and Technology），2009，30（4）：285－289.

Adaptive control of chaos based on compressive sensing

ZHAO Ying－bao1，HUANG Li－min2
（1.College of Electrical Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China；2.Modern Education Technology Center，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

An adaptive chaos control method is proposed，using compressed sensing to identify equations and parameters of chaotic systems based only on the output time series，and using negative feedback control of chaotic system to set goals.Lorenz and the R?ssler system is used to illustrate the identfication and control of equations and parameters of the time－varying structure system.First the Lorenz system is controlled to a fixed point or periodic oscillations.When the structure changes to R?ssler，the new structure and its parameters is recognized，and the system retruns to the control objectives again.The results show that，compared to least－squares method，the method can be realized with less data，while the model structure and parameters are estimated with high accuracy.Then negative feedback can be used to control rapidly the system to the set goals.

compression sensing；negative feedback control；model estimation；chaos control；parameter estimation

TP273＋.2

A

1008－1542（2012）03－0248－05

2011－12－24；責任編輯：陳書欣

趙英寶（1972－），男，河北張家口人，講師，主要從事電力電子、模糊控制方面的研究。