卡諾圖化簡數(shù)學新方法

葉 騰，朱桂英

（1.上海交通大學安泰經(jīng)濟與管理學院，上海 200240；2.河北工程大學裝備制造學院，河北邯鄲 056029）

卡諾圖化簡數(shù)學新方法

葉 騰1，朱桂英2

（1.上海交通大學安泰經(jīng)濟與管理學院，上海 200240；2.河北工程大學裝備制造學院，河北邯鄲 056029）

提出了卡諾圖化簡中獲得卡諾圈合并結(jié)果的數(shù)學方法。根據(jù)卡諾圖制圖原理，這種數(shù)學計算方法的要點在于：用2個最小項對應(yīng)的十進制數(shù)之差找到消去變量；從卡諾圈的某個最小項中去掉相應(yīng)消去變量得到合并結(jié)果。該方法在卡諾圖（尤其變量數(shù)較多的）化簡中，能更準確、更迅速地獲得卡諾圈合并結(jié)果，并可應(yīng)用于計算機輔助卡諾圖化簡邏輯函數(shù)。

卡諾圖；應(yīng)用數(shù)學方法；簡化法

邏輯函數(shù)化簡是數(shù)字邏輯和數(shù)字電路分析中的重要內(nèi)容，目前主要有代數(shù)化簡法、表格化簡法和卡諾圖化簡法。代數(shù)方法是基于布爾代數(shù)基本運算公式進行化簡的方法，這種方法要求操作者掌握一定的技巧，并對最簡結(jié)果有一定的判斷能力。卡諾圖化簡法是6個以下變量邏輯函數(shù)化簡最簡便而常用的方法。

近年來，人們對卡諾圖進行了多方面的研究和拓展，包括卡諾圖鏡像畫圈法［1］、最小項使用的重復次數(shù)識別技巧［2］、填圖技巧［3］、卡諾圖降維簡化法［4］、卡諾圖的計算機輔助實現(xiàn)［5］等方法，對如何快速、準確地確定卡諾圈合并項結(jié)果卻沒有很好的解決方法，導致在實際應(yīng)用（尤其是在四變量、五變量、六變量卡諾圖中）時，人們?nèi)菀谆煜兞课恢茫灾抡`讀最小項合并結(jié)果。筆者提出的卡諾圖化簡數(shù)學方法可解決上述問題。

1 基本步驟

1.1 畫卡諾圖

在“與 －或”表達式的基礎(chǔ)上，畫出邏輯函數(shù)的卡諾圖，步驟如下［6］：

1）畫出函數(shù)變量的卡諾圖。

2）在圖中標示每一個乘積項所包含的最小項，就得到邏輯函數(shù)的卡諾圖。

其中，如果乘積項為最小項，則可直接轉(zhuǎn)換成數(shù)字代碼對應(yīng)填入卡諾圖。在二進制對應(yīng)數(shù)中，原變量代表該位為1，反變量代表該位是0。這樣將乘積項（即最小項）轉(zhuǎn)化為二進制對應(yīng)數(shù)，再將二進制數(shù)轉(zhuǎn)化為十進制數(shù)，填入對應(yīng)編號的小方格中。如，AB′C＝101＝5，所以填入m5。如表達式不是最小項表達式，但是“與－或”表達式可將其先轉(zhuǎn)化成最小項表達式，再填入卡諾圖，再按上述規(guī)則填入。也可根據(jù)乘積項是最小項的公因子這一特點直接觀察填入。

1.2 畫卡諾圈

畫圈規(guī)則與傳統(tǒng)卡諾圈規(guī)則相似，具體規(guī)則如下［7］：

在標示出的相鄰最小項中畫圈，盡量畫大圈，但每個圈內(nèi)只能含有2n（n＝0，1，2，…）個相鄰項。要特別注意對邊相鄰性和四角相鄰性。

圈的個數(shù)盡量少。在新畫的包圍圈中至少要含有1個未被圈過的標識方格，否則該包圍圈是多余的。卡諾圖中所有標示過的方格均要被圈過，即不能漏下標示過的最小項。

1.3 合并卡諾圈中的最小項

任意選取卡諾圈中的最小項，寫出由變量組成的邏輯式（由于系數(shù)小的最小項邏輯式相對容易寫，所以一般選取卡諾圈中系數(shù)最小的最小項）。然后找出卡諾圈中系數(shù)之差為2n的所有差值，從邏輯式中消去所有差值對應(yīng)位的變量。如miniterm1＝x1，miniterm2＝x2，w＝log2｜x1－x2｜＋1，則消去從右至左第w位的變量。將所有差值對應(yīng)變量消去后的邏輯式即為卡諾圈合并結(jié)果。

1）對包含2n個最小項的卡諾圈來說，只需要找到n種不同的2n的差，如1，2，4，8等，然后將這些差所代表的變量從卡諾圈中系數(shù)較小的最小項中去掉，即為該圈的最終合并結(jié)果。

2）找差技巧：①將左上角的數(shù)，先分別和它右相鄰數(shù)、下相鄰數(shù)作差，再分別和圈中首行行尾、首列列尾數(shù)作差，這5個位置一般就可以把差找全；②將圈中最大數(shù)減去最小數(shù)，并將差表示成若干個2n的和，每一個2n必定是一種兩項差。

1.4 寫出最簡“與 －或”表達式

將所有卡諾圈的計算結(jié)果相與（用加號相連），即為最終合并結(jié)果。

2 實例展示

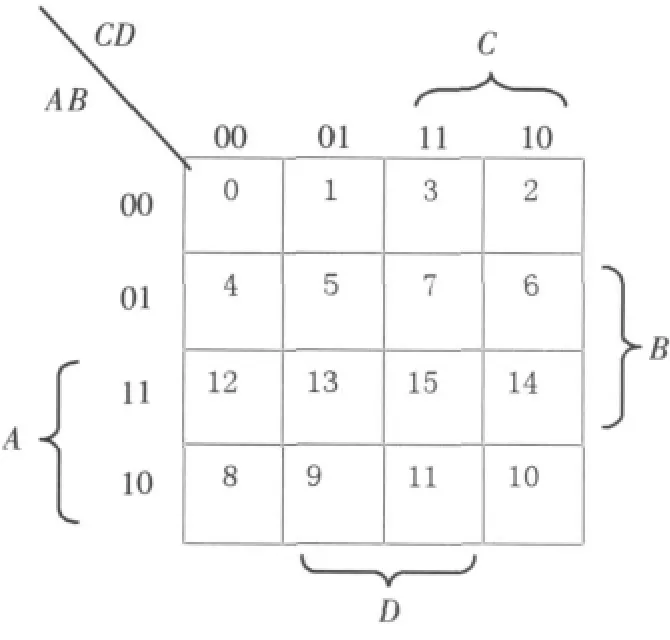
圖1 四變量卡諾圖Fig.1 Four－variable map

例1［8］化簡F（A，B，C，D）＝∑（0，1，2，6，8，9，10）。

解 傳統(tǒng)方法如下：

第1步，畫出四變量卡諾圖，見圖1。

第2步，畫出傳統(tǒng)卡諾圖，見圖2，觀察對應(yīng)變量，計算邏輯函數(shù)結(jié)果。

新算法見圖3，其中A為8，B為4，C為2，D為1，圖中有以下3個卡諾圈。

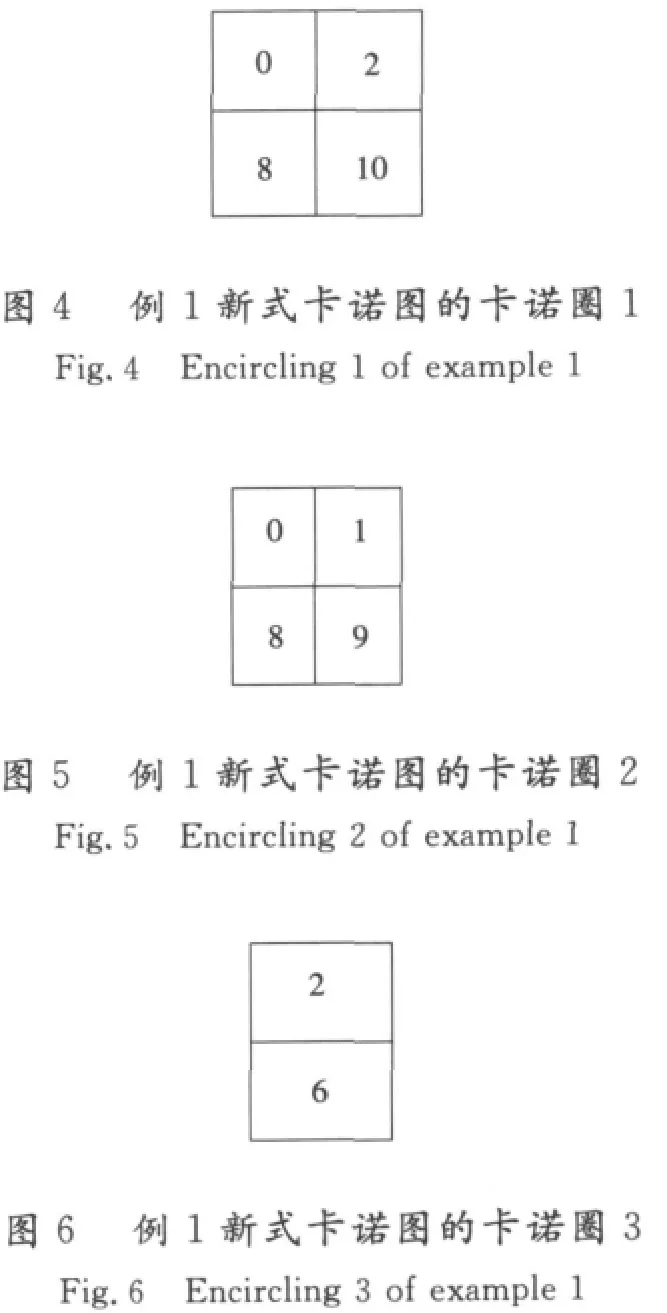
卡諾圈1（見圖4）：min｛0，2，8，10｝＝0＝A′B′C′D′，該卡諾圈包含4個最小項，4＝22，因此需要找2個不同的2的冪的差。8－0＝8，所以消掉的變量是A；2－0＝2，所以消掉的變量是C。消掉A，C，為B′D′。

卡諾圈2（見圖5）：min｛0，1，8，9｝＝0＝A′B′C′D′，該卡諾圈包含4個最小項，4＝22，因此需要找2個不同的2的冪的差。1－0＝1，所以消掉的變量是D；8－0＝8，所以消掉的變量是A；A′B′C′D′中消掉A，D，為B′C′。

卡諾圈3（見圖6）：6－2＝4所以消掉的變量是B，min｛2，6｝＝2＝A′B′CD′，消掉B為A′CD′。所以原函數(shù)結(jié)果是F（A，B，C）＝∑（0，1，2，6，8，9，10）＝B′C′＋B′D′＋A′CD′。

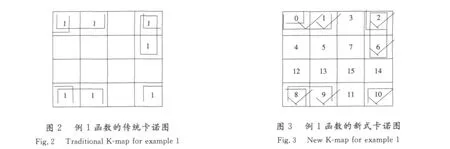
例2 化簡F（A，B，C，D，E）＝∑（4，5，6，7，9，11，13，15，16，24，27，31）。

解 傳統(tǒng)方法如下.

第1步，畫出五變量卡諾圖，見圖7。

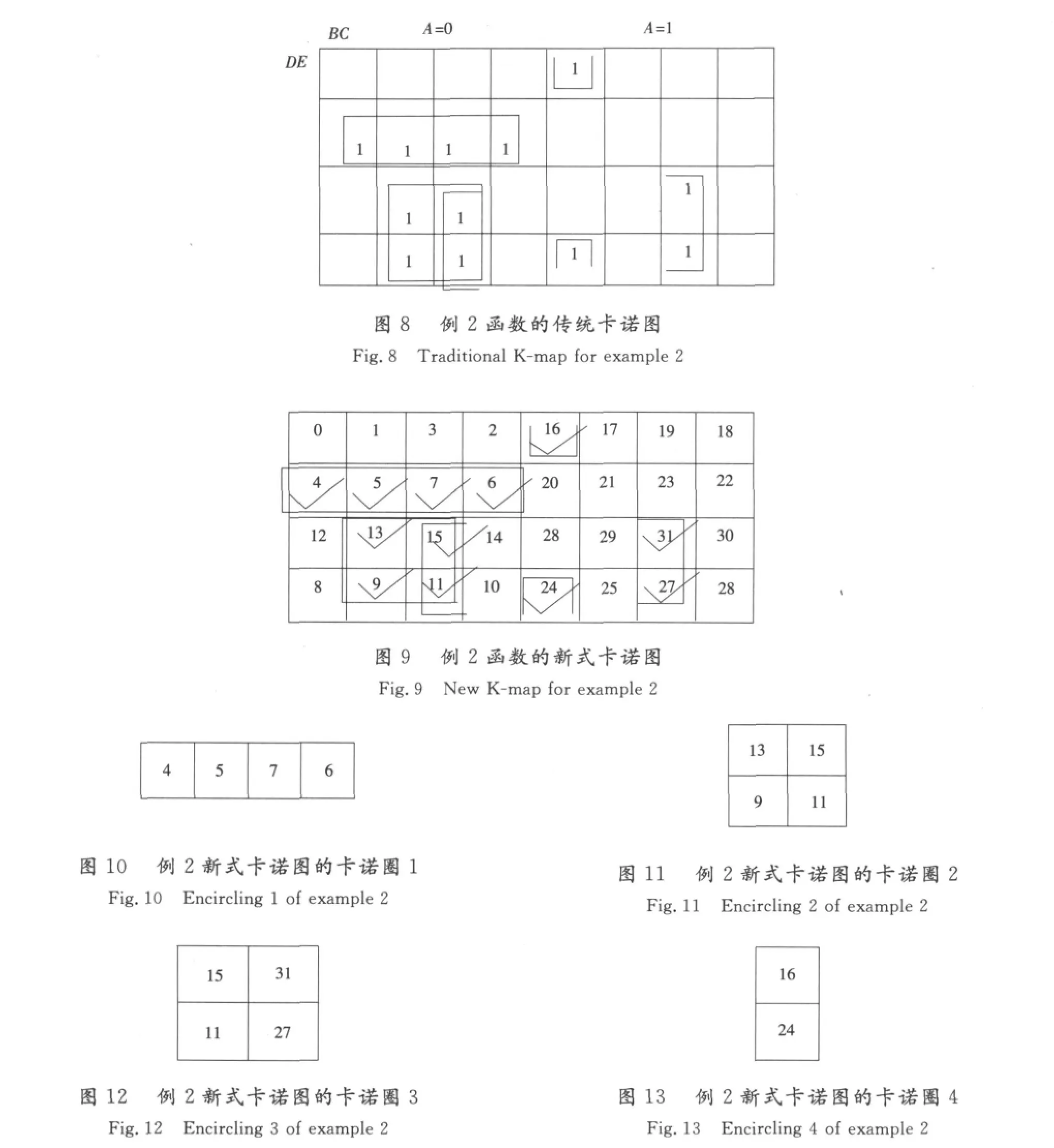
第2步，畫出對應(yīng)函數(shù)的傳統(tǒng)卡諾圖見圖8。可見五變量用傳統(tǒng)的卡諾圖已經(jīng)很難快速分辨合并后的結(jié)果。

卡諾圖化簡新方法計算如下（見圖9）。

變量對應(yīng)十進制數(shù)為A：16，B：8，C：4，D：2，E：1；圖中共4個卡諾圈。

卡諾圈1（見圖10）：min｛4，5，6，7｝＝4＝A′B′CD′E′。該卡諾圈包含4個最小項，4＝22，因此需要找2個不同的2的冪的差。5－4＝1，消掉的變量是E；6－4＝2，消掉的變量是D；A′B′CD′E′消掉D，E，即A′B′C。

卡諾圈2（見圖11）：min｛9，11，13，15｝＝9＝A′BC′D′E。該卡諾圈包含4個最小項，同理需要找2個不同的2的冪的差。13－9＝4，消掉的變量是C；15－13＝2，消掉的變量是D；消掉變量C，D，即A′BE。

卡諾圈3（見圖12）：min｛15，31，11，27｝＝11＝A′BC′DE。該卡諾圈包含4個最小項，同理需要找2個不同的2的冪的差。15－11＝4，消掉的變量是C；31－15＝16，消掉的變量是A；消掉A，C，即BDE。

卡諾圈4（見圖13）：24－16＝8，所以消掉的是C。min｛16，24｝＝16＝AB′C′D′E′，消掉C，即AB′D′E′。

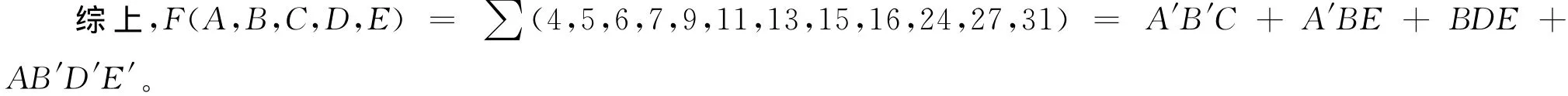
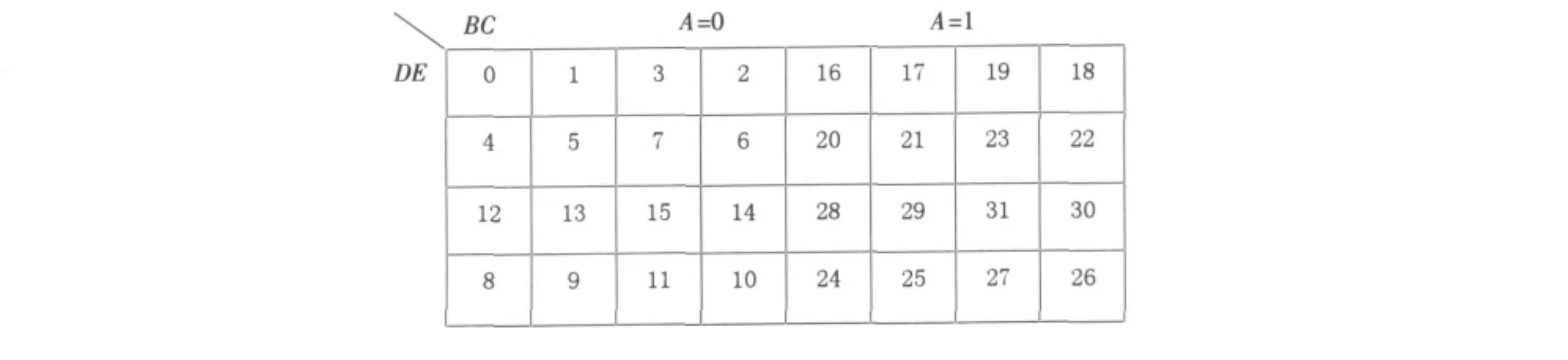
圖7 五變量卡諾圖Fig.7 Five－variable map

3 結(jié) 論

本文提出的卡諾圖化簡新方法是通過找到卡諾圈中系數(shù)較小的最小項并結(jié)合作差消元法確定卡諾圈中各項的合并結(jié)果，進而最終確定邏輯函數(shù)合并結(jié)果的邏輯函數(shù)簡化法。該方法具有以下優(yōu)點：

1）不需通過肉眼查找變量就能確定卡諾圈合并結(jié)果的簡單易行的數(shù)學方法。即通過卡諾圈中最小項對應(yīng)十進制數(shù)作差確定消去變量，再結(jié)合卡諾圈中系數(shù)最小的最小項最終合并結(jié)果。

2）普通卡諾圖總共需畫2張圖，1張對應(yīng)變量數(shù)的基本卡諾圖，1張只包含0或1的函數(shù)卡諾圖，填圖需要先將最小項所對應(yīng)的十進制表格標出，再另畫1張圖并在相應(yīng)位置標0或1。而筆者提出的新方法只需畫1張圖，省略了另畫圖標0或1的步驟，可直接在十進制表格上操作。節(jié)省了1個步驟，可以使效率進一步提高。

3）由于這種方法基于作差與大小比較這2種數(shù)學運算，故可以在卡諾圖的計算機輔助化簡中大大簡化邏輯運算。

［1］ 宋海聲.化簡邏輯函數(shù)的新方法［J］.西北師范大學學報（自然科學版）（Journal of Northwest Normal University（Natural Science）），2002，38（3）：37－41.

［2］ 韓建華.卡諾圖化簡多函數(shù)的簡便方法［J］.華東地質(zhì)學院學報（Journal of East China Geological Institute），1998，21（4）：392－395.

［3］ 江素云.使用卡諾圖的技巧［J］.科協(xié)論壇（Science ＆Technology Association Forum），2009（12）：104－105.

［4］ 郭煥銀.談降維卡諾圖化簡邏輯函數(shù)的方法［J］.淮南師范學院學報（Journal of Huainan Teachers College），2001，3（2）：5－6.

［5］ 喻國平.邏輯函數(shù)的計算機輔助卡諾圖化簡［J］.南昌大學學報（工科版）（Journal of Nanchang University（Natural Science）），1996，18（3）：51－53.

［6］ 朱定華.數(shù)字電路與邏輯設(shè)計［M］.北京：清華大學出版社，2011.

［7］ 吳繼娟.數(shù)字邏輯［M］.北京：人民郵電出版社，2008.

［8］ MORRIS M M.Computer System Architecture［M］.3rd ed.London：Prentice－Hall International，2002.

New mathomatical simplification method of Karnaugh map

YE Teng1，ZHU Gui－ying2
（1.Antai College of Economics and Management，Shanghai Jiaotong University，Shanghai 200240，China；2.Equipment Manufacturing College，Hebei University of Engineering，Handan Hebei 056029，China）

A mathematical method is provided to get the combination solution of variables in the encircling of Karnaugh map.Based on the basic theory of K－map，two key points of the method are：Ascertaining the complementary variables by the differences of the corresponding decimal indexes of the two miniterms；Eliminating the complementary variables from the corresponding miniterm in the encircling and qetting get the combination results.The method provides more efficient and accurate way to simplify logic functions based on K－map.It can also be applied to Karnaugh map of any number of variables and to simplification by K－map with computer assistance.

Karnaugh map；mathematical method；simplification method

O142

A

1008－1542（2012）03－0202－05

2012－02－17；責任編輯：張 軍

葉 騰（1990－），女，河北大城人，主要從事信息系統(tǒng)及管理方面的研究。

朱桂英副教授。E－mail：Zhu0gui0ying＠163.com