基于粗糙商集的邊坡穩定性模糊積分評價

方宏偉，李長洪，方玲玲

(1.北京科技大學 a.金屬礦山高效開采與安全教育部重點實驗室;b.土木與環境工程學院，北京 100083;2.蘇州大學計算機科學與技術學院，江蘇蘇州 215006)

1 研究背景

邊坡穩定性分析方法有很多種，由于其影響因素的數據難以精確確定，故基于非確定性理論的一類理論模型［1］是較合理的。如李文秀［2］提出了礦山邊坡的模糊數學方法。王艷霞［3］認為對邊坡穩定分析這一不確定性問題，采用模糊數學方法更符合客觀實際，選取反映問題實質的隸屬函數是亟需解決和重點研究的問題;并提出最穩妥的確定方法應該是模糊統計，而權重直接影響決策，目前多憑主觀經驗獲取，會導致失真，層次分析法 AHP(Analytic Hierarchy Process)為解決問題的一個途徑。黃飄［4］認為模糊綜合評判是其中一種廣泛使用方法，但方法本身無突破性進展，而精確的隸屬函數應采用模糊統計法建立，AHP法的難點在于判斷矩陣的確定。蘇永華［5］也認為模糊統計方法確定隸屬函數具有較大的準確性，指出困難在于大量樣本的實現。可見應用模糊數學方法評價邊坡穩定性的難點是隸屬度和權重的計算。

粗糙集理論［6］具有處理不確定性問題時不需要數據之外任何先驗信息的優點，因此本文在已有研究成果的基礎上提出了對粗糙集理論中的屬性商集作模糊統計，求解模糊隸屬度的集值統計方法(這里將邊坡狀態作為決策屬性而其它因素作為條件屬性)。其特點是以邊坡穩定狀態為內涵，以其它因素為外延，使其結果更符合樣本實際，降低求解過程中人為主觀因素，可與已有的研究成果來驗證其可靠性。同時，以神經網絡正交試驗［7］求得的各因素對穩定性影響級差之差為依據，構建AHP判斷矩陣來計算權重［8］，并與該試驗結論作對比分析。相對于其它模糊數學方法，模糊積分(Sugeno積分)特別適合于度量和決策問題［9］，可用其評價邊坡穩定性，由邊坡樣本數據的回判及與其它理論方法結果和工程實際來驗證其可行性。

2 邊坡穩定性影響因素模糊隸屬度的求解

2.1 樣本數據離散和屬性商集的求解

本文搜集了邊坡樣本共121個，按編號分別來源于:參考文獻［10］(1-82)(為圓弧破壞)，文獻［11］(83-108)，文獻［12］(109-121);穩定性影響因素5個:重度γ(kN/m3)、黏聚力c(kPa)、摩擦角 φ (°)、坡度 α (°)、坡高 H(m);判別因素 1個:安全系數F;狀態S:以0表示破壞，1表示穩定。說明:考慮到其它樣本中相關因素數量，僅取文獻［12］中部分樣本，按原文順序排列如下(對含有子樣本的樣本從上到下再次編號):13，2，3，41，42，5，6，72，82，92，93，101，11。

為了求屬性商集，首先要對樣本數據離散化，盡管粗糙集理論中的相關方法很多，但最可靠還是應用邊坡穩定性分析的專業知識，已有的模糊分析方法中因素的評判分級標準為其提供了幫助，但尚無統一的標準。本文根據已有的研究成果并依據樣本數值范圍，采用表1的分級標準對其進行離散化。如前所述，其中條件屬性即為穩定性影響因素和判別因素，決策屬性為邊坡狀態S。說明:為了克服原參考文獻中邊界值為兩個級別的弊端，采取越大越優型屬性(γ，c，φ，F)大值增大相應一個單位和越小越優型屬性(α，H)小值減小相應一個單位來劃分不同級別，分級后的樣本數據(部分)見表2。

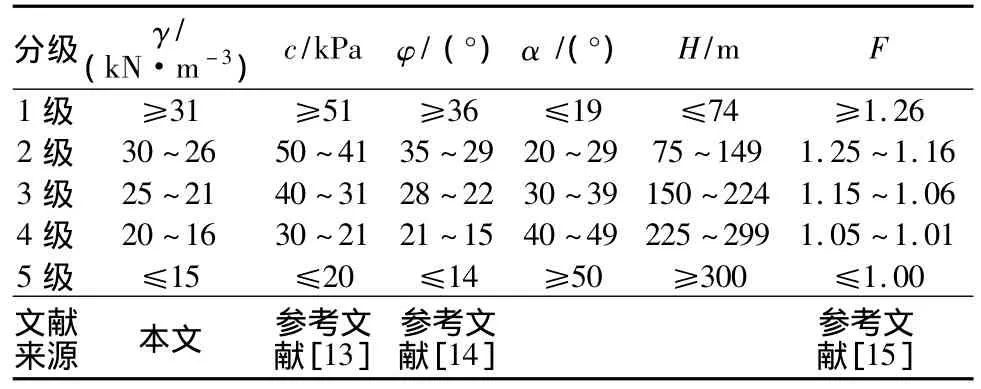
表1 條件屬性值分級標準Table 1 Classification standards of condition attribute values

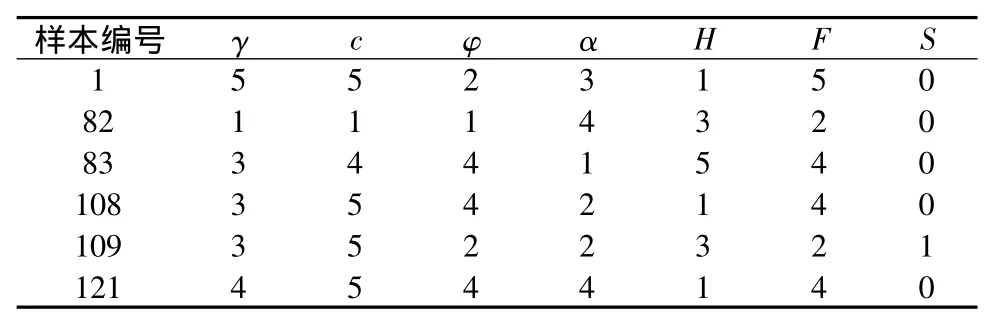
表2 離散后的樣本數據(部分)Table 2 Discrete sample data(portion)

為描述方便，設 Ci(j)=(γ(j)，c(j)，φ(j)，α(j)，H(j)，F(j))，其中 i=1～6表示條件屬性，j=1～5表示級別。分級后的樣本是有重復的，可采用粗糙集軟件Rosetta［6］對條件屬性求商集后簡化，剩余84個相容決策樣本，再對各級別屬性求商集U/IND(Ci(j))，計算界面見圖1。

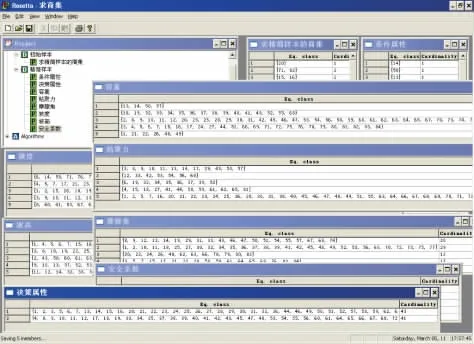
圖1 Rosetta計算界面Fig.1 Interface of Rosetta computing

2.2 模糊隸屬度的求解

首先分析用粗糙商集作集值統計求解隸屬度符合模糊統計試驗應具備的4個要素［9］:①論域U={Ci(j)}，即條件屬性的集合;②U中一個固定元素Ci(j)，即一定級別的條件屬性;③U上一個模糊概念，即邊坡狀態S(決策屬性)，對其不確定性統計形成了條件屬性商集U/IND(Ci(j))與決策屬性商集U/IND(S)的交集，設A為該交集中的單個元素(即單個邊坡樣本)，則A的每次選擇(固定化)就是對邊坡狀態的一次確切劃分，即該邊坡樣本為何種狀態(破壞0或穩定1)，表現了各因素(外延)對邊坡狀態(內涵)的隸屬關系;④條件，影響邊坡狀態的因素，制約A的選擇(運動)。

該試驗的基本特點是Ci(j)固定，A變化。U/IND(Ci(j))的基即為Ci(j)固定次數n，可定義為求Ci(j)隸屬度的試驗次數，在以求0或1狀態的隸屬度為條件選擇A(使A變化)，擊中Ci(j)(或Ci(j)捕捉到A)的次數為n0或n1，則對破壞狀態的隸屬度為μ0(Ci(j))=n0/n，對穩定狀態的隸屬度為μ1(Ci(j))=n1/n。定義要求n取無窮大，實際一個邊坡樣本是不同級別屬性的組合，n是有一定規模的，這可以從樣本數據離散后出現重復得到驗證。下面通過求γ(3)的隸屬度來說明計算過程:由對應商集的基可知道3級別γ的樣本個數n=33，求其與決策屬性商集U/IND(S)的交集，可知樣本中邊坡破壞個數n0=14和穩定個數n1=19，則n0/n表示γ(3)對破壞狀態0的隸屬度 μ0(γ(3))=0.42，n1/n表示γ(3)對穩定狀態1的隸屬度μ1(γ(3))=0.58。各級別條件屬性隸屬度計算結果見表3。

2.3 模糊隸屬度的驗證

選取安全系數 F的隸屬度進行驗證，文獻［16-17］已經對其作了深入的研究，方法是依據已有的安全系數F與邊坡狀態S物理關系的研究結論，從常用的隸屬函數中選取戒下型嶺形分布函數，并各自根據工程經驗及樣本實例確定其函數參數。需要說明的是，文獻［17］的樣本也來源于文獻［10］，但剔除了安全系數為1.8的破壞邊坡一例。將F(j)代入文獻中的隸屬函數求得隸屬度，并與本文結果相對比，見表4。可見本文求得F(1)的隸屬度位于區間值以內，其余均位于區間值上限，只是在小數點后的第2位不同，當然采用的樣本數據不同，計算結果不可能完全一致，總體上本文的模糊隸屬度還是可靠。由于其它因素隸屬度是用同樣方法求得，故可認為也是合理的。對 γ(1)和 c(2)及α(5)的隸屬度為1的情況，說明本文樣本有一定的局限性，也再次表明邊坡狀態是由不同級別屬性共同作用決定的。

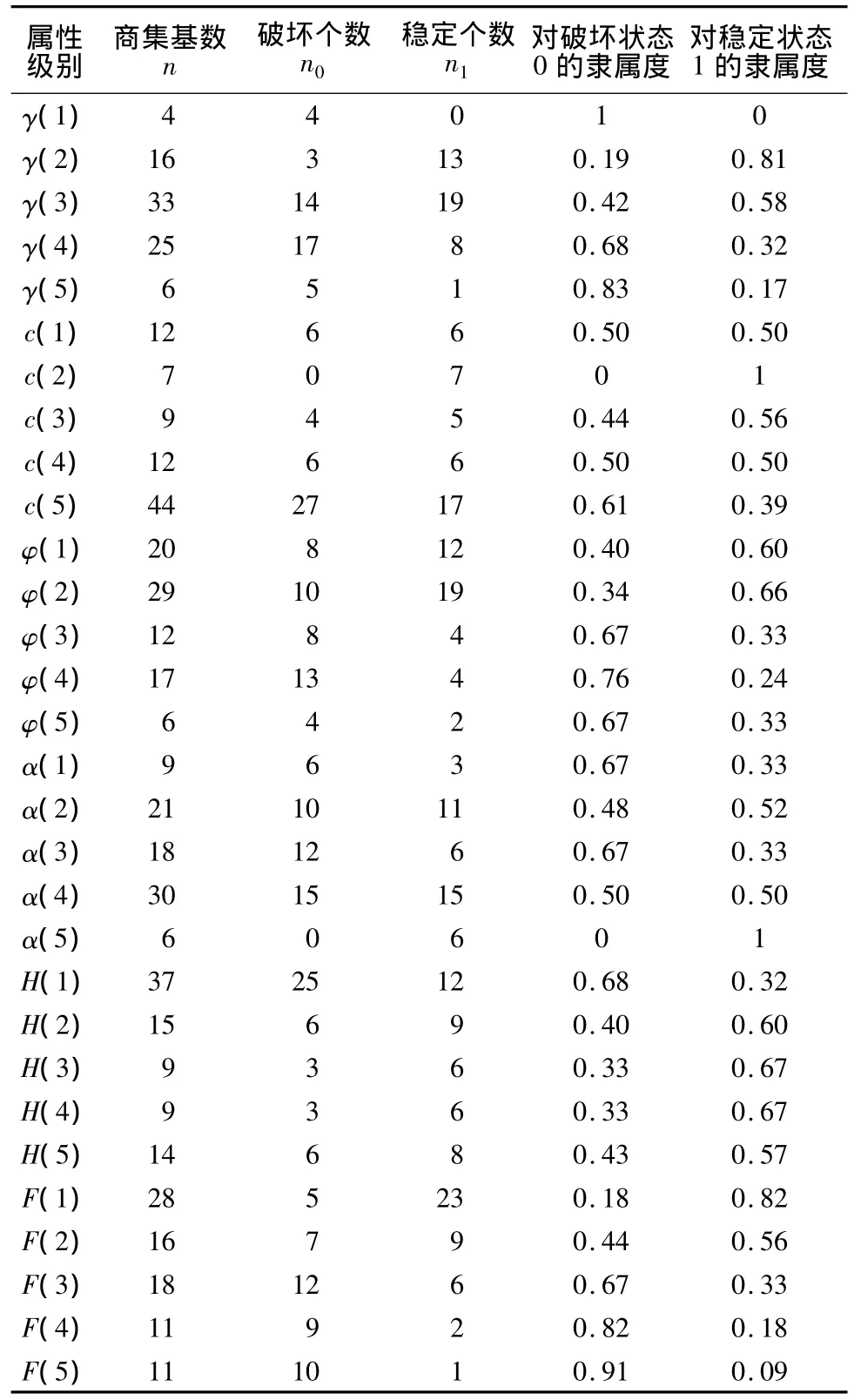
表3 不同級別條件屬性的隸屬度Table 3 Membership degrees of condition attributes in different levels

表4 安全系數F隸屬度的對比驗證Table 4 Comparison and verification of membership degree of safety factor F

3 邊坡穩定性的模糊積分評價

3.1 因素權重的確定

神經網絡正交分析得到的因素對邊坡穩定性影響級 差 值 為 (0.818(γ)，0.972(c)，1.19(φ)，0.342(α)，0.608(H))，用大值與小值的差值作為AHP判斷矩陣構建的依據，即若級差之差不超過0.2標度為2(equally to moderately more important)，不超過0.3標度為 3(moderately more important)，不超過0.4標度為 4(moderately to strongly more important)，不超過0.5標度為5(strongly more important)，不超過0.6標度為6(strongly to very strongly more important)，不超過0.7標度為 7(very strongly more important)，超過0.8標度為8(very strongly to extremely more important)，當小值與大值比較時則為相應標度的倒數。

采用SD(Super decision)［18］軟件計算，見圖2。四舍五入得5個因素權重向量為ω(Ci)=(0.15，0.24，0.50，0.04，0.07)，這與文獻［7］的結論是一致的。即邊坡穩定性的主要影響因素為φ，c以及γ，其它為次要影響因素;φ的敏感性高于c，γ和α，H;c的敏感性高于γ;γ的敏感性均高于α，H;而H敏感性高于α。F是由以上5個因素求得的，也是邊坡穩定性評價的重要判別因素，其權重應與前5個因素權重之和相等，可得6個因素的權重向量為ω(Ci，F)=(0.08，0.12，0.25，0.02，0.04，0.49)。

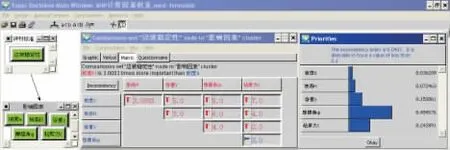
圖2 SD計算因素權重Fig.2 Interface of the calculated factors’weights in software SD

3.2 模糊積分評價方法與應用

在模糊積分評價前，需按隸屬度大小對各因素重新排列，如樣本1重排列后各因素的排序見表5。由于本文評價因素為6個，為有限情形下的模糊積分，公式［9］為

式中:E1為評價值;u1(i)為因素對穩定狀態的隸屬度;為因素權重累加。如果公式中取u0(i)，則評價值為 E0，且 E1+E0=1;因此將0.5作為評價臨界值，考慮到臨界狀態是偏于危險的，故定義E1＞0.5為穩定狀態1，E0≤0.5為破壞狀態0。以樣本1為例說明計算過程。ωi計算如下:

ω1=ω(1)=0.25，

ω2=ω(1)+ ω(2)=0.37，

ω3=ω(1)+ ω(2)+ ω(3)=0.39，

ω4=ω(1)+ ω(2)+ ω(3)+ ω(4)=0.43，

ω5=ω(1)+ ω(2)+ ω(3)+ ω(4)+ ω(5)=0.51，

ω6=ω(1)+ ω(2)+ ω(3)+ ω(4)+ ω(5)+ ω(6)=1。

則按模糊積分公式計算E1=0.37，為破壞狀態0，與實際相符。

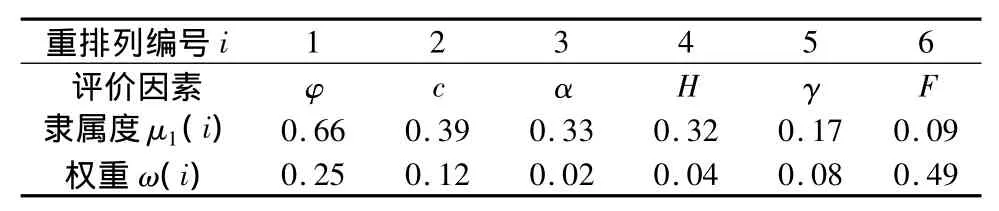
表5 因素重排列Table 5 Factors re-arranged

為了驗證方法的可行性以及因素多少對評價結果正確率的影響，對84個樣本依次按沒有F和有F進行評價(兩者區別在于權重的不同)，可知:缺少F時評價正確60個，正確率71.4%;有F時，正確64個，正確率76.2%。可見因素的多少對結果的正確率有一定的影響，因素越多則評價的正確率越高。從樣本的選取也可以證明這一點，文獻［12］有的樣本在本文的6個因素取值相同的情況下，由于其它因素取值的不同而使其狀態不同，如前所述即邊坡的穩定狀態是由多種因素共同作用的結果，不局限于本文6個因素。由于樣本的限制，本文只能選取6個因素求隸屬度作模糊積分評價。選取樣本以外的5個邊坡工程實例作模糊積分評價(表6)，可見評價結果可靠。

表6 邊坡工程實例數據和模糊積分評價結果Table 6 Data of real slope engineering examples and results of fuzzy integral evaluation

4 結論

邊坡穩定性影響因素的確定包含很大不確定性，而在應用非確定性理論模型，如模糊數學方法評價時，存在隸屬度和權重難以確定的問題。

本文提出了對粗糙集理論中的屬性商集作模糊統計求解隸屬度的集值統計算法，降低了人的主觀因素影響;與已有研究成果對比表明，該方法的結果是可靠的。以神經網絡正交試驗分析得到的各因素對邊坡穩定性影響級差之差作為AHP判斷矩陣建立的依據來求權重，其結果與該試驗的結論相一致。引進了更適合度量和決策的模糊積分理論，對邊坡樣本的分析表明:模糊積分評價結果正確率與因素多少成正向關系;與其它理論方法的結果和工程實際對比可知，該方法評價結果可靠，但計算過程更方便快捷。另外，進一步擴充樣本，使所計算得到的模糊隸屬度更準確以及與隨機可靠性相結合是以后的研究重點。同時，在給定相應充足的樣本情況下，本文提出的方法還可應用于評價地基、基坑、地下工程等不同類型工程的穩定性。

［1］李文秀，梅松華.斜坡穩定性評價的一類非確定性理論模型［J］.長江科學院院報，2004，21(1):15-17.(LI Wen-xiu，MEI Song-hua.An Indeterminacy Theoretical Model for Evaluation of Slope Stability［J］.Journal of Yangtze River Scientific Research Institute，2004，21(1):15-17.(in Chinese))

［2］李文秀.礦山高陡邊坡穩定性研究的模糊數學方法［J］.長江科學院院報，1996，13(增刊):34-36.(LI Wen-xiu.Fuzzy Mathematics of the Stability of High and Steep Mining Slope［J］.Journal of Yangtze River Scientific Research Institute，1996，13(Sup.):34-36.(in Chinese))

［3］王艷霞.模糊數學在邊坡穩定分析中的應用［J］.巖土力學，2010，31(9):3000-3004.(WANG Yan-xia.Application of Fuzzy Mathematics to Slope Stability Analysis［J］.Rock and Soil Mechanics，2010，31(9):3000-3004.(in Chinese))

［4］黃 飄，謝曉峰，李 挺.邊坡巖體穩定性的模糊綜合評判方法綜述［C］∥巖石力學與工程的創新和實踐.第十一次全國巖石力學與工程學術大會論文集，武漢:中國科學院武漢巖土力學研究所，2010:235-241.(HUANG Piao，XIE Xiao-feng，LI Ting.Review of Fuzzy Comprehensive Evaluation Methods for Slope Rock Mass Stability［C］∥ Innovations and Practices of Rock Mechanics and Engineering:Proceedings of the 11th National Academic Conference on Rock Mechanics and Engineering.Wuhan:Institute of Rock and Soil Mechanics，Chinese Academy of Sciences，2010:235-241.(in Chinese))

［5］蘇永華.巖土參數模糊隸屬函數的構造方法及應用［J］.巖土工程學報，2007，29(12):1772-1779.(SU Yong-hua.Constructing Method of Fuzzy Membership Function of Geotechnical Parameters and Its Application［J］.Chinese Journal of Geotechnical Engineering，2007，29(12):1772-1779.(in Chinese))

［6］?HRN A.Discernibility and Rough Sets in Medicine:Tools and Applications［D］.S?r-Tr?ndelag:Norwegian U-niversity of Science and Technology，1999.

［7］夏元友，熊海豐.邊坡穩定性影響因素敏感性人工神經網絡分析［J］.巖石力學與工程學報，2004，23(16):2703-2707.(XIA Yuan-you，XIONG Hai-feng.Sensitivity Analysis of Slope Stability Based on Artificial Neural Network［J］.Chinese Journal of Rock Mechanics and En-gineering，2004，23(16):2703-2707.(in Chinese))

［8］SAATY T L.Making and Validating Complex Decisions with the AHP/ANP［J］.Journal of Systems Science and Systems Engineering，2005，14(1):1-36.

［9］常大勇，張麗麗.經濟管理中的模糊數學方法［M］.北京:北京經濟學院出版社，1995:172-179.(CHANG Da-yong，ZHANG Li-li.Fuzzy Mathematic Methods in E-conomic Management［M］.Beijing:Peking Economic College Press，1995:172-179.(in Chinese))

［10］馮夏庭.智能巖石力學導論［M］.北京:科學出版社，2000:239-240.(FENG Xia-ting.Intelligent Rock Mechanics Introduction［M］.Beijing:Science Press，2000:239-240.(in Chinese))

［11］汪華斌，徐瑞春.BP神經網絡在魚洞河滑坡穩定性評價中的應用［J］.長江科學院院報，2002，19(4):62-64.(WANG Hua-bin，XU Rui-chun.Application of BP Artificial Neural Networks on Stability Evaluation of Yudonghe Landslide［J］.Journal of Yangtze River Scientific Research Institute，2002，19(4):62-64.(in Chinese))

［12］陳樂求，彭振斌，陳偉，等.基于模糊控制的人工神經網絡模擬在土質邊坡安全預測中的應用［J］.中南大學學報(自然科學版)，2009，40(5):1381-1387.(CHEN Le-qiu，PENG Zhen-bin，CHEN Wei，et al.Artificial Neural Network Simulation on Prediction of Clay Slope Stability Based on Fuzzy Controller［J］.Journal of Central South University(Science and Technology)，2009，40(5):1381-1387.(in Chinese))

［13］王秀麗，王艷紅，朱彥鵬.黃土地區高邊坡穩定性模糊識別法理論與應用［J］.巖石力學與工程學報，2006，25(增1):2868-2874.(WANG Xiu-li，WANG Yan-hong，ZHU Yan-peng.Theory and Application of Fuzzy Pattern Recognition to Stability of Loess Slope［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(Sup.1):2868-2874.(in Chinese))

［14］彭文祥.巖質邊坡穩定性模糊分析及耒水小東江電站左岸滑坡治理研究［D］.長沙:中南大學，2004.(PENG Wen-xiang.Fuzzy Analysis of Rock Slope Stability and Landslide Treatment on the Left Bank of Xiaodongjiang Power Station［D］.Changsha:Central South University，2004.(in Chinese))

［15］包惠明.基于RS理論的巖質路塹邊坡穩定性研究［D］.西安:長安大學，2003.(BAO Hui-ming.Rock Slope Stability Based on RS Theory［D］.Xi’an:Chang’an University，2003.(in Chinese))

［16］王 宇，宋新龍，張 行.邊坡工程模糊隨機可靠度分析［J］.長江科學院院報，2011，28(9):30-34.(WANG Yu，SONG Xin-long，ZHNAG Hang.Fuzzy Stochastic Reliability Analysis of Slope Engineering［J］.Journal of Yangtze River Scientific Research Institute，2011，28(9):30-34.(in Chinese))

［17］徐 輝.基于模糊集理論的邊坡穩定模糊隨機可靠度分析［D］.杭州:浙江大學，2006.(XU Hui.Fuzzy Reliability Analysis of Slope Stable Capacity Based on Fuzzy Sets［D］.Hangzhou:Zhejiang University，2006.(in Chinese))

［18］SAATY R W.Decision Making in Complex Environments:The Analytic Hierarchy Process(AHP)for Decision Making and the Analytic Network Process(ANP)for Decision Making with Dependence and Feedback［M］.Pittsburgh:Katz Graduate School of Business，University of Pittsburgh，2003.

［19］王東耀，折學森，葉萬軍.基于可拓工程法的黃土路塹邊坡穩定性評價方法［J］.地球科學與環境學報，2006，28(3):57-60.(WANG Dong-yao，SHE Xue-sen，YE Wan-jun.Method for Stability of Loess Slope of Cut Based on Topology［J］.Journal of Earth Sciences and Environment，2006，28(3):57-60.(in Chinese))