超球體平方根平淡卡爾曼濾波及其應用

王躍鋼，蔚 躍，雷堰龍，陳蘇邑

（解放軍第二炮兵工程大學自動化系，陜西 西安 710025）

0 引言

初始對準對于慣導系統(tǒng)的精度與啟動準備時間有著直接的關系，所以一直被看作慣性導航技術領域的重要問題之一［1］。捷聯(lián)慣導系統(tǒng)（strap－down inertial navigation system，SINS）初始對準的實質就是確定載體坐標系到真實導航坐標系的轉換矩陣。由于初始對準誤差將嚴重影響系統(tǒng)的整體誤差，因此要求初始對準的對準精度要高，對準時間要短。采用卡爾曼濾波是實現(xiàn)慣導系統(tǒng)自對準的有效途徑之一，但卡爾曼濾波使用的條件是只能用于線性系統(tǒng)，對于非線性系統(tǒng)常用的方法是采用擴展卡爾曼濾波（extended kalman filter，EKF），而在大方位失準角情況下，這種近似線性化的方法舍棄了非線性函數(shù)的高階項，引入了誤差，使濾波結果為次優(yōu)，甚至導致濾波發(fā)散［2］。Julier［3］等人從非線性均值和方差傳播的角度提出平淡卡爾曼濾波（unscented kalman filter，UKF），這種方法直接利用非線性模型進行遞推估計，避免了線性化誤差的引入且遞推估計過程不需計算矩陣，但隨著狀態(tài)空間維數(shù)的增加，計算量也會急劇增大，加重系統(tǒng)計算負擔，同時無法保證在濾波更新階段生成的狀態(tài)協(xié)方差陣非負定［4］，從而直接影響采樣點生成時進行的Cholesky分解。為此，本文提出超球體平方根平淡卡爾曼濾波方法，解決上述問題。

文章第一、二章為基礎鋪墊，第三章將超球體采樣及平方根濾波結合提出一種新的濾波方法，并應用到捷聯(lián)慣導系統(tǒng)大失準角下的非線性誤差模型中，第四章通過matlab數(shù)值仿真，分別與EKF和UKF進行了對比，說明了新方法的可行性。

1 捷聯(lián)慣導系統(tǒng)非線性誤差方程

1.1 速度誤差方程

式中，W為量測噪聲，B為噪聲驅動陣。

大失準角下的速度誤差方程為［5］：

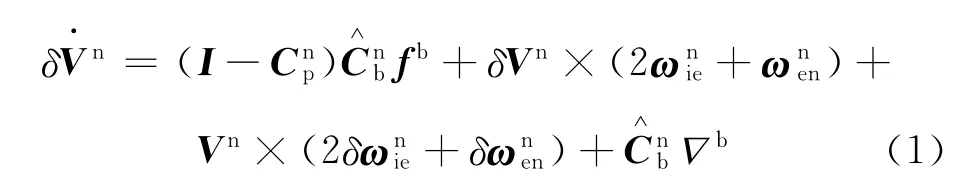
令歐拉失準角φx，φy，φz的轉動順序為φz、φx、φy。則可求得C由式（2）確定：

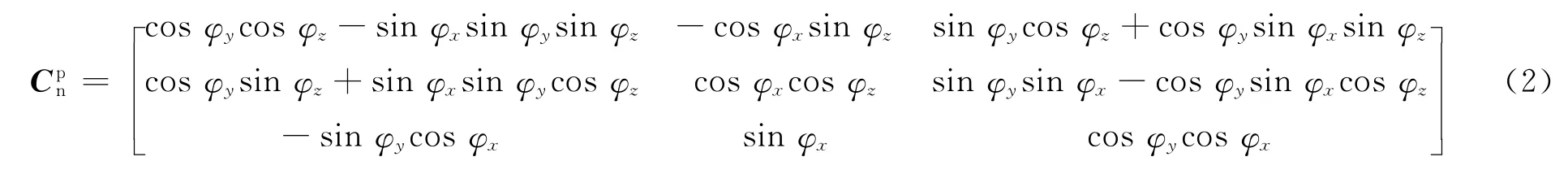
1.2 姿態(tài)誤差方程

大失準角下姿態(tài)誤差方程為［5］：

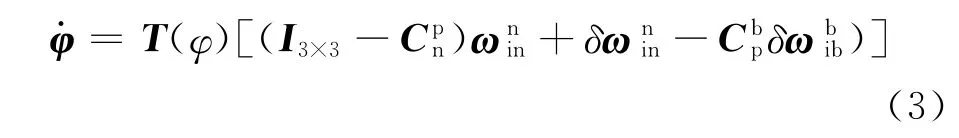
1.3 非線性對準濾波模型

假設陀螺和加速度計誤差僅由常值漂移εb＝［εbxεbyεbz］T，▽b＝ ［▽bx▽by▽bz］T和觀測噪聲εg＝ ［εgxεgyεgz］T，▽r＝ ［▽rx▽ry▽rz］T組成，忽略其他因素的影響，可以表示為：

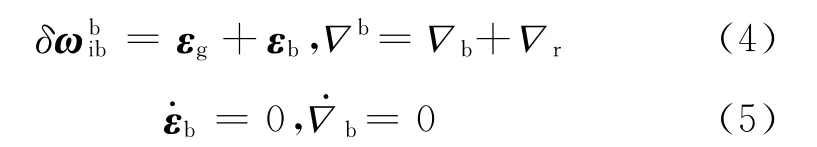
選取狀態(tài)變量為：

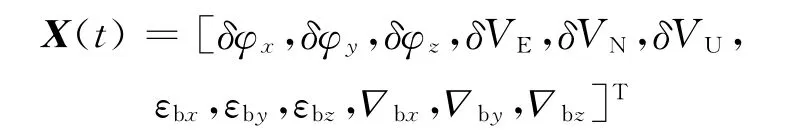
式（1）、式（3）、式（5）組成了大失準角下SINS誤差狀態(tài)方程。

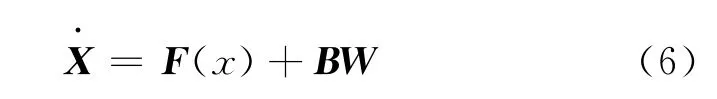
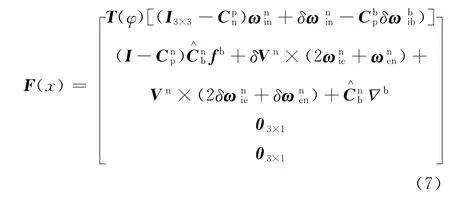
取速度誤差為觀測量得到SINS觀測方程為：

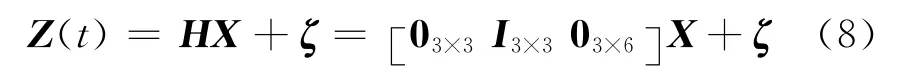
式（8）中，ζ為觀測噪聲。

式（6）、式（8）構成了非線性對準的濾波模型。

2 超球體采樣及平方根濾波

2.1 超球體分布采樣點變換方法

Julier等人［3］從非線性均值和方差傳播的角度提出UKF，這種方法直接利用非線性模型進行遞推估計，避免了線性化誤差的引入，且遞推估計過程不需計算矩陣，比EKF更為簡單，后來又提出了超球體分 布 采 樣 點 變 換 （spherical simplex unscented transformation，SSUT）方法［6］，減少采樣點的求取，將采樣點數(shù)目由2n＋1減小到n＋2，當系統(tǒng)維數(shù)很大時可以極大地降低計算量［7］。同時SSUT中采樣點具有與狀態(tài)相同的前二階矩。SSUT采樣點的選取步驟如下：

1）選擇第0個權值W0，并且0≤W0≤1

2）計算其他權值

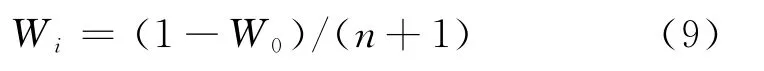
3）初始化一維化狀態(tài)序列

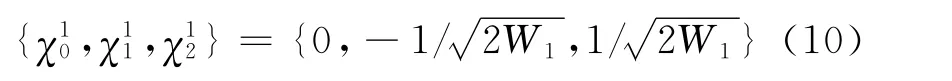
4）空間維數(shù)j＝2，3，…，n時，遞推公式為：

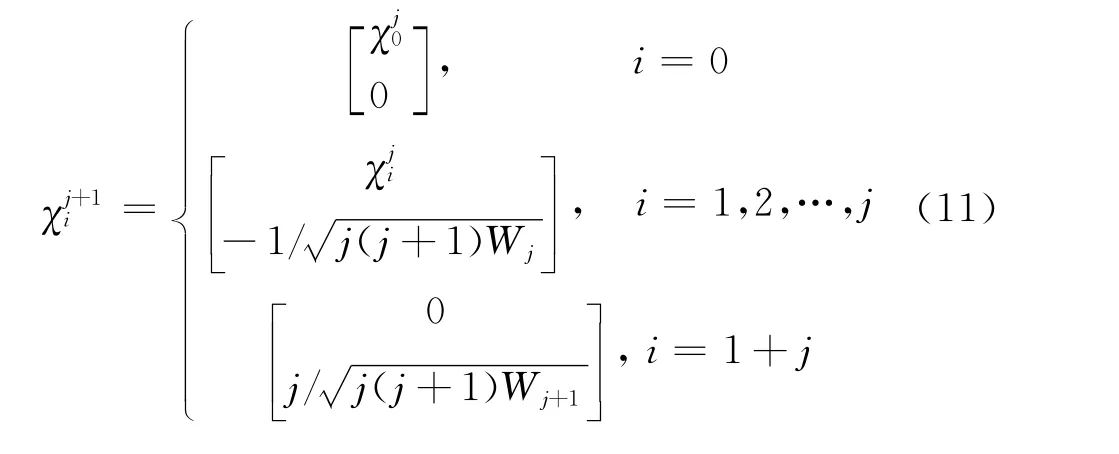
2.2 平方根平淡卡爾曼濾波算法

由于在標準UKF濾波狀態(tài)更新階段，P陣很容易失去正定性［8］。造成協(xié)方差陣P 無法進行Cholesky分解，不能生成采樣點。采用平方根平淡卡爾曼濾波解決此問題，該方法在UKF濾波的時間更新和量測更新階段采用平方根濾波將狀態(tài)估計誤差協(xié)方差陣的Cholesky因子形式Sa直接傳遞，避免了在采樣點計算時對狀態(tài)估計誤差協(xié)方差陣的Cholesky分解，從而解決了UKF數(shù)值不穩(wěn)定性的問題，減小了計算量。

3 超球體平方根平淡卡爾曼濾波算法

改進的平淡卡爾曼濾波算法是SSUT方法與平方根UKF結合的方法，這里稱之為超球體平方根平淡卡爾曼濾波算法，取超球體采樣的首字母以及平方根的第二個字母，該算法英文縮寫為SRUKF（spherical root unscented kalman filter）。

不妨設非線性系統(tǒng)的模型如式（13）：

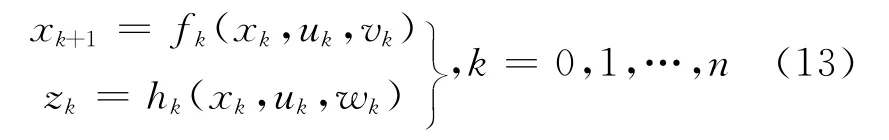
式中，過程噪聲wk是均值為0，方差為Q的高斯白噪聲。同樣，量測噪聲vk為均值為0，方差為R的高斯白噪聲。

1）初始化

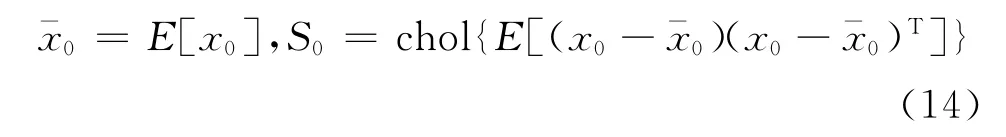
2）計算采樣點

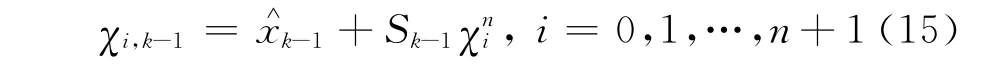
3）時間更新

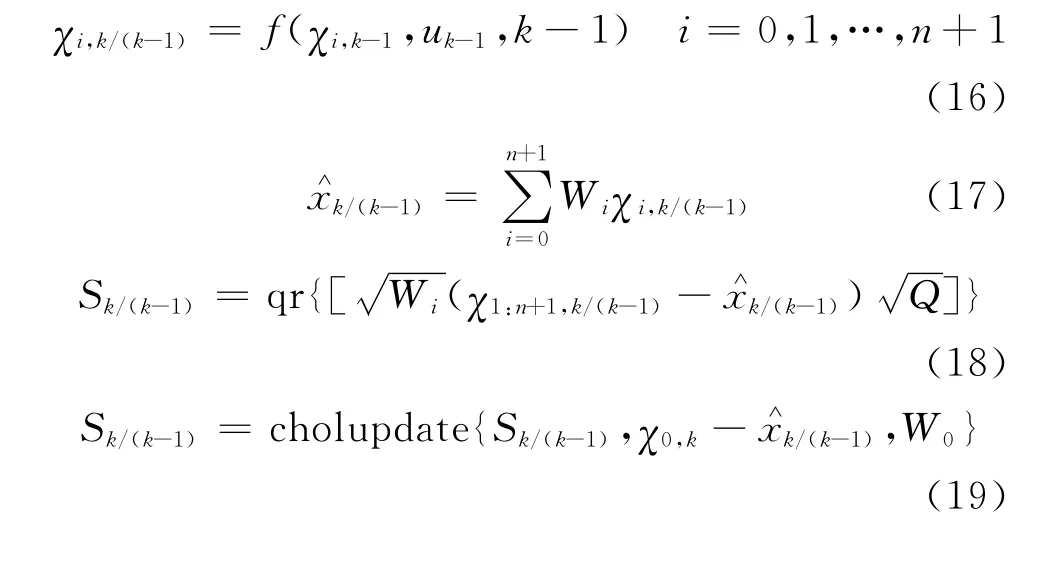
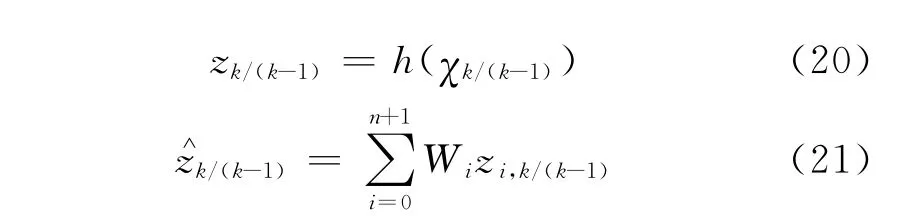
4）量測更新

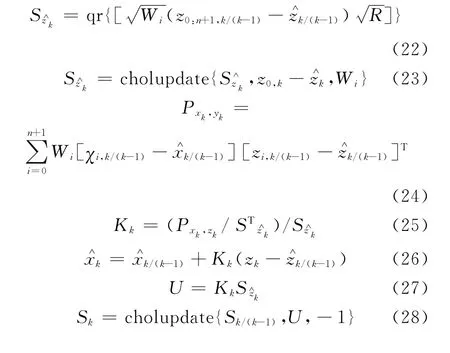
4 仿真分析

仿真初值按照如下選取：東向、北向、天向失準角分別取2°，2°，15°；陀螺常值漂移取0.02 （°）／h，隨 機 漂 移 為 0.01 （°）／h；加 速 度 計 常 值 漂 移 為1×10－4g，緯度取45°，當?shù)馗叨?50m，仿真時間400s，SINS采樣周期取0.05s。

按照以上仿真條件分別進行EKF，SRUKF，UKF濾波，仿真結果如表1和圖1—圖3所示。

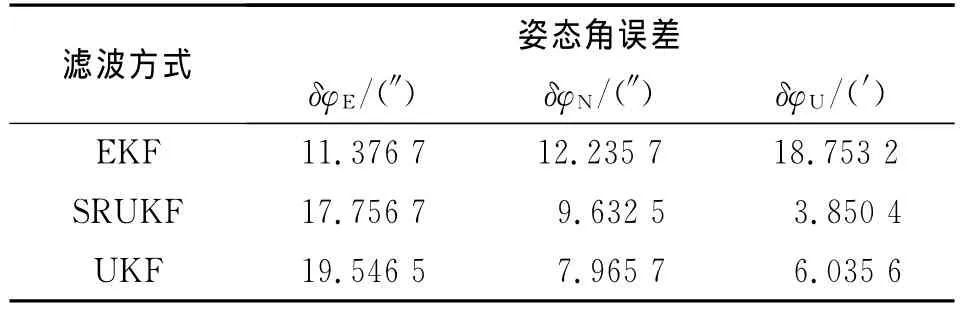
表1 捷聯(lián)慣導系統(tǒng)的初始對準穩(wěn)態(tài)均值Tab.1 Steady state mean of SINS initial alignment

其中，表1穩(wěn)態(tài)均值是250～350s仿真結果取絕對值后的均值。這段時間內(nèi)，濾波進入穩(wěn)態(tài)沒有了符號的變化，為了比較穩(wěn)態(tài)值偏移0的距離，因此都取絕對值，100s時間段內(nèi)求均值的目的是為了有效地克服單個奇異點帶來的影響，不會對仿真結果造成影響。

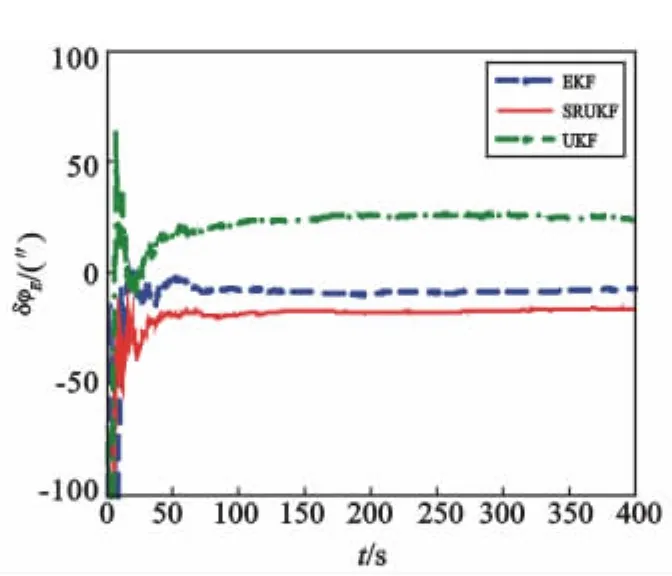
圖1 東向誤差角估計值Fig.1 Error estimation of east angle

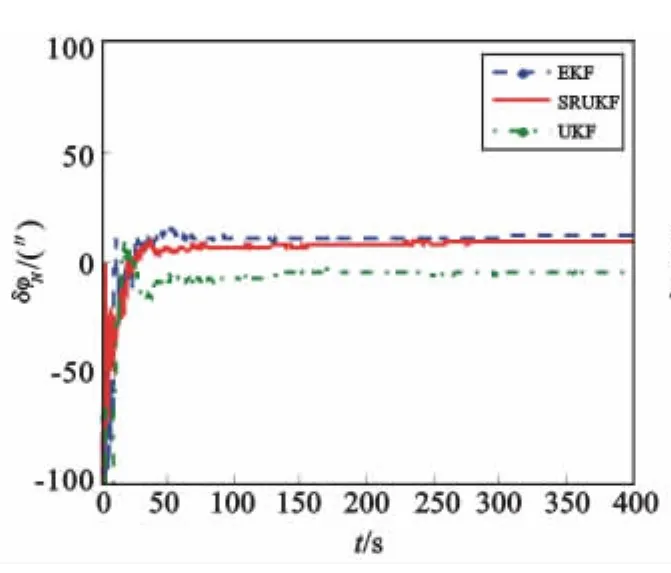
圖2 北向誤差角估計值Fig.2 Error estimation of north angle

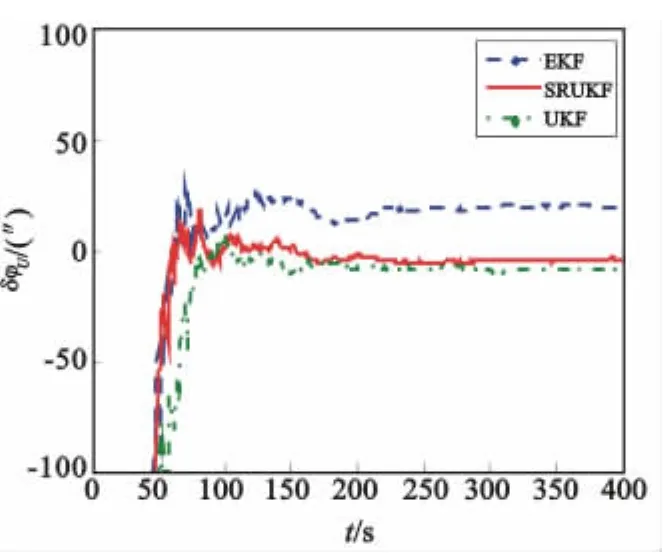
圖3 天向誤差角估計值Fig.3 Error estimation of attitude angld

捷聯(lián)慣導系統(tǒng)在該初始條件下水平（東向與北向）誤差角的理論穩(wěn)態(tài)誤差值為18.73″，天向理論穩(wěn)態(tài)誤差值為4.46′。仿真結果表明：水平誤差角仿真結果與理論分析的效果相符，三種濾波方法水平失準角誤差很小，收斂時間也很快，這是因為水平失準角是小角度。其次，對于初始對準的核心部分方位角的對準精度而言，表1指出SRUKF與UKF的濾波結果相對于EKF來講與理論值更為接近，這從圖3也可以直接看出，這是因為SRUKF和UKF在處理非線性系統(tǒng)的精度能達到二階，而EKF在處理非線性問題上是按照泰勒級數(shù)展開取一階的線性化方法，其精度只能達到一階，要想達到更高精度就必須得求復雜的雅克比矩陣。因此，雅克比矩陣的求取是限制EKF精度的主要因素。最后，圖3中SRUKF的收斂時間要比UKF快，原因是采樣點數(shù)目由2n＋1減小到n＋2，系統(tǒng)維數(shù)較大時可以減小計算量。綜上可知，SRUKF相對于EKF提高了濾波精度，相對于UKF縮短了對準時間，這種改進的方法提高了對準效率。

5 結論

提出了超球體平方根平淡卡爾曼方法，該方法是通過SSUT與平方根濾波結合，解決了UKF數(shù)值不穩(wěn)定性的問題，同時當系統(tǒng)維數(shù)較大時降低了計算量。將超球體平方根平淡卡爾曼濾波方法應用到SINS大失準角下的初始對準當中，仿真結果表明：SRUKF對于EKF能有效提高方位失準角對準精度，由18.75′提高到了3.85′；相對于 UKF雖然精度差不多，但是減少了采樣點，減小了計算量，提高了計算效率，是一種理想的濾波方法。

［1］鄧正隆.慣性導航原理［M］.哈爾濱：哈爾濱工業(yè)大學出版社，1994.

［2］李濤.非線性濾波方法存導航系統(tǒng)中的應用研究［D］.長沙：國防科技大學，2003.

［3］Hovland G E，Von Hoff T P，Gallestey E A.Nonlinear estimation methods for parameter tracking in power plants［J］.Control Engineering Practice，2005（13）：1 341－1 345.

［4］NING Xiaolin，F(xiàn)ANG Jiangcheng.An autonomous celestial navigation for LEO salellite based on unscented kalman filter and information fusion［J］.Aerospace Science and Technology，2007（11）：222－228.

［5］龍瑞，秦永元，趙長山.簡化SPKF在捷聯(lián)慣導系統(tǒng)非線性對準中的應用［J］.壓電與聲光，2010，32（5）：746－749.LONG Rui，QIN Yongyuan，ZHAO Changshan.Application of simplified SPKF in non－linear alignment of SINS［J］.Piezoelectrics ＆ Acoustooptics，2010，32（5）：746－749.

［6］Julier S J，Uhlmann J K.Reduced sigma point filters for the propagation of means and covariance through nonlinear transformations［C］／／AACC Proceedings of American Control Conference，2002：887－892

［7］Simon J Julier.The spherical simplex unscented transformation［J］.Proceddings of the IEEE American Control Conference，Denver Colorado，2003：2 430－2 434

［8］SONG Qi，HAN Jianda.An adaptive UKF algorithm for the state and parameter estimations of a mobile robot［J］.Acta Automatica Sinica，2008，34（1）：72－79.