基于壓縮感知的認知雷達高分辨成像

孫鳳蓮，張 群，羅 迎，顧福飛，朱 豐

（空軍工程大學信息與導航學院，陜西 西安 710077）

0 引言

傳統(tǒng)雷達通常采用固定的發(fā)射信號，并通過接收端的自適應處理及濾波算法的設計來提高系統(tǒng)性能。對于日益復雜的電磁環(huán)境和密集雜波、多目標背景等挑戰(zhàn)，當環(huán)境發(fā)生變化時，僅靠接收端的自適應處理已很難獲得理想的成像效果。同時，當前的硬件技術(shù)水平（如相控陣雷達）也已為實現(xiàn)雷達系統(tǒng)發(fā)射端的自適應提供了良好的基礎。在此背景下，加拿大的S.Haykin教授于2006年首次提出了“認知雷達”的概念［1］，并已逐漸引起了雷達領域?qū)W者的注意與興趣。參考國內(nèi)外已有的對于認知雷達最優(yōu)波形設計方法的研究［2－3］，本文從目標所處成像環(huán)境對成像精度的不同要求出發(fā)，提出了一種基于壓縮感知的認知雷達高分辨成像方法。

1 基于壓縮感知的稀疏線性調(diào)頻步進信號高分辨距離像

壓縮感知［4］（Compressive Sensing，CS）是近年來提出的一種全新的信號處理理論，目前已被廣泛應用于高分辨成像雷達［5－7］中，為解決雷達成像中高分辨率與高采集率之間的矛盾提供了有效途徑。其中，稀疏線性調(diào)頻步進信號（SFCS）是常用的一種信號形式，其構(gòu)成相當于隨機保留原SFCS脈沖串內(nèi)的一部分，即M（ M＜N）個子脈沖，載波步進頻率＝Li·Δf，且滿足L1＝0，LM＝N－1。設雷達成像過程中共需要發(fā)射MT個脈沖串，其第m個脈沖串的第i個子脈沖信號為：

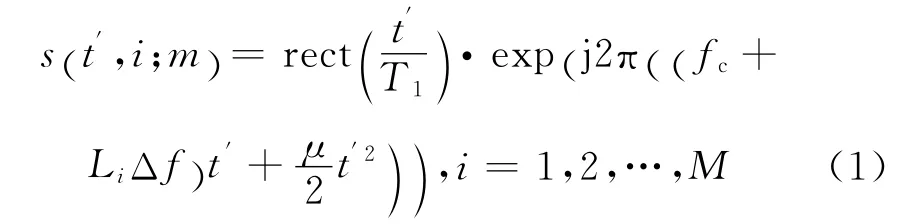
式中，t′＝t－mNTr－iTr，fc＋iΔf是第i個子脈沖的載頻，μ為調(diào)頻斜率，T1為子脈沖寬度。

按傳統(tǒng)方法對回波信號在距離向作“dechirp”處理，得到目標回波的稀疏表示形式為：

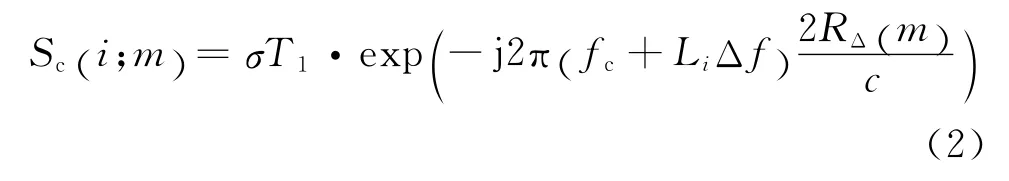
此時，由于信號載頻不是按規(guī)律步進的，利用傳統(tǒng)方法已無法得到目標的高分辨距離像（HRRP）。但如果目標上散射點在距離向是離散的，則信號Sc（i；m）在頻譜上將是稀疏的［8］，可通過CS理論對其進行重構(gòu)處理。設目標的徑向信息即HRRP為S （Ff；m），建立稀疏基矩陣Ψ ，具體形式為：

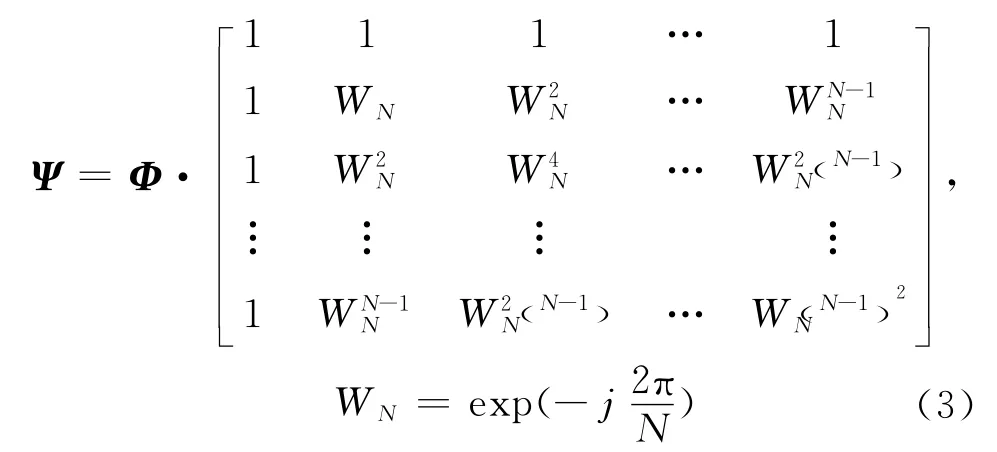
式中，Φ為隨機部分單位矩陣，且滿足

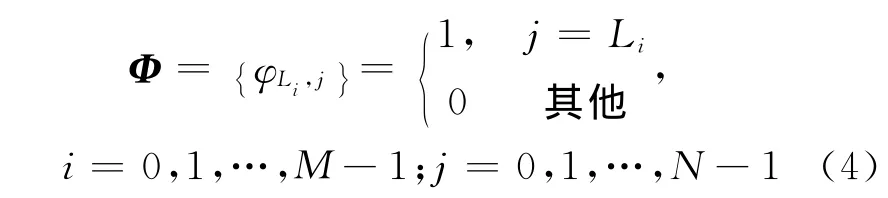
文獻［8］從理論上證明了基于隨機采樣并利用部分DFT矩陣重構(gòu)稀疏信號的可行性。所以，只要觀測維數(shù)足夠大，采用正交匹配追蹤（Orthogonal Matching Pursuit，OMP）算法即可以高概率重構(gòu)出目標徑向信息S （Ff；m）。OMP算法的重構(gòu)質(zhì)量與觀測維數(shù)有關(guān)。一般地，當觀測維數(shù)M滿足以下不等式時，通過該算法即可高概率的重構(gòu)出原始信號［9］

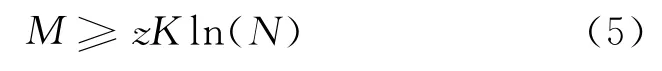
式中，z為較小的常數(shù)。

2 基于壓縮感知的認知雷達自適應稀疏成像

在第1章成像方法中，M作為稀疏SFCS的一個重要參數(shù)，與目標散射點的稀疏度K密切相關(guān)，也即在利用CS對目標HRRP進行重構(gòu)時，極可能需要目標稀疏度K這一先驗知識。這與認知雷達的理論基本是一致的，因而可利用接收端到發(fā)射端的反饋信息自適應地調(diào)整對K的估計值，進一步調(diào)整發(fā)射信號波形，實現(xiàn)與目標環(huán)境的最優(yōu)匹配。

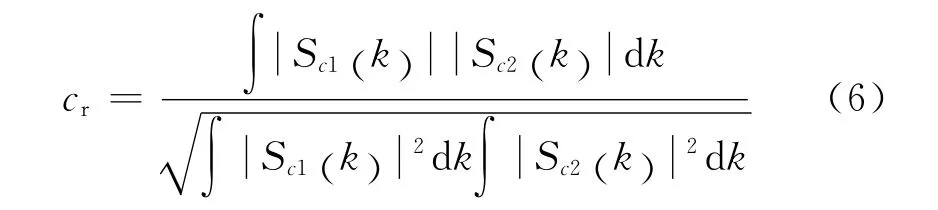
式中，Sc1（k）和Sc2（k）為相鄰兩次目標距離像。設經(jīng)驗門限值Th，若cr＜Th，則認為對K的估計值較小，后續(xù)需增大；反之，則認為估計值較大，可利用重構(gòu)的目標HRRP實現(xiàn)對目標當前稀疏度的認知。同時，為克服OMP算法的重構(gòu)誤差，在對cr進行計算時，選用相鄰多次（設為m次）目標高分辨距離像的平均值代替單次高分辨距離像。其具體成像過程為：

1）：依照文獻［10］中的方法，發(fā)射一個僅含有少量（設為N′）子脈沖的傳統(tǒng)SFCS脈沖串，得到目標的一個粗分辨HRRP，并大致估計目標徑向稀疏度（i ＝0）。

4）：通過式（6）計算相鄰目標HRRP的相關(guān)系數(shù)cr，若cr＜Th，則令＝＋a（a＞0）；反之，則計算重構(gòu)HRRP中幅值較大的散射點的數(shù)Ki，并令＝Ki。

5）：對目標像重構(gòu)次數(shù)進行判斷。若i＜MT，則令i＝i＋1，并轉(zhuǎn)2）；否則，把重構(gòu)得到的MT個序列按順序排成矩陣＝ ［，…，］，完成對目標HRRP的認知成像。

3 仿真驗證

為驗證本文成像方法的有效性，采用圖1飛機散射點模型進行仿真。該模型徑向長度約16m，徑向上的散射點坐標數(shù)約50個。初始時刻與雷達的距離為10km，飛行速度為300m／s。雷達發(fā)射信號為SFCS，載頻為10GHz，脈沖串重復頻率PRF＝250Hz，頻率步進階數(shù)N＝512，頻率步進量Δf＝2.343 8MHz，合成帶寬B＝1.2GHz，對應距離分辨率Δr＝0.125m。設定目標成像時間為2s，成像過程中共發(fā)射500個脈沖串，獲得方位向分辨率Δa＝0.25m。

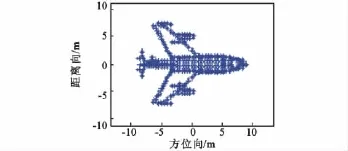
圖1 飛機目標散射點模型Fig.1 Scatter model of the air target

雷達發(fā)現(xiàn)目標后，首先發(fā)射一組含有少數(shù)子脈沖的傳統(tǒng)SFCS，這里取N′＝17，對應的距離分辨率Δr′＝3.765m，采用傳統(tǒng)方法合成目標的一個粗分辨HRRP，如圖2（a）所示。取距離像幅度的閾值Tα＝0.2，得到目標的徑向長度估計值為5個距離單元，即≈18.825m，此時，對應的稀疏度最大值Kmax＝／Δr≈150。設對目標距離向稀疏度的初始估計值為＝20 （＜Kmax），由公式（5）得到＝138，通過OMP算法重構(gòu)得到目標的一個HRRP如圖2（b）所示。顯然，由于對目標稀疏度的估計值太小，兩次得到的目標HRRP重構(gòu)誤差均較大，且相似度很低，在后續(xù)成像過程中需增大對K的估計值。

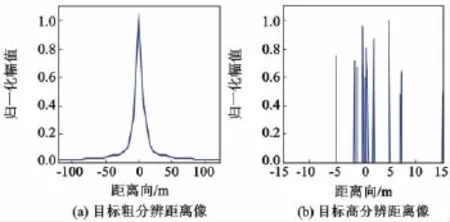
圖2 目標粗、高分辨距離像Fig.2 Target＇s Coarse－RRP、target's HRRP

仿真實驗中，分別取m＝10，a＝3，Th＝0.9。由圖3（a）可以看出，在本次成像過程中，系統(tǒng)根據(jù)對目標徑向稀疏度K的認知實現(xiàn)了對自身參數(shù)的50次調(diào)整，并使cr始終保持在0.85～0.95之間。圖3（b）為通過該認知方法重構(gòu)出的第200個HRRP，它有效地描述了飛機目標在距離向上的特征。對圖3（a）所示自適應稀疏條件下重構(gòu)得到各次目標HRRP作方位向的傅里葉變換，即可得到目標ISAR二維像，成像結(jié)果如圖3（c）所示。可以看出，在滿足成像精度的前提下，本次成像過程中信號子脈沖數(shù)量的減少十分明顯，平均每次利用的稀疏子脈沖數(shù)為211個，僅占512個可用子脈沖數(shù)的41.21%，有效節(jié)省了雷達頻譜資源。

在認知雷達系統(tǒng)中，發(fā)射波形不僅能夠根據(jù)目標稀疏特性自適應調(diào)整，而且能夠根據(jù)當前任務及目標所處環(huán)境進行最優(yōu)配置。在多任務條件下，對系統(tǒng)處理的實時性要求相對較高而對目標成像精度的要求相對較低，此時，可通過降低T2值的設置來實現(xiàn)，如取T2＝0.75，得到雷達自適應稀疏成像結(jié)果如圖4所示。與圖3相比，在該成像精度要求下，雷達成像所需子脈沖數(shù)更少，僅為149個，大幅節(jié)省了雷達頻譜資源。但由于觀測次數(shù)較低，重構(gòu)出的目標ISAR像有部分散射點缺失，但并不影響對目標的有效識別。

以上仿真實驗都是基于無噪條件下進行的，但通常，目標所處環(huán)境都有一定的噪聲存在。當雷達接收端信噪比為－5dB時，其相應的稀疏度估計及頻譜自適應稀疏曲線如圖5（a）所示，得到的ISAR成像結(jié)果如圖5（b）所示。可知，在本次成像過程中，由于目標信號共經(jīng)過了兩次能量的相干積累，成像質(zhì)量并未受到噪聲影響，但由于噪聲的存在，為達到相鄰相關(guān)系數(shù)Th＝0.9的成像精度，平均每次發(fā)射SFCS脈沖串中的稀疏子脈沖數(shù)為283個，較無 噪條件下更多，符合目標成像的實際環(huán)境。

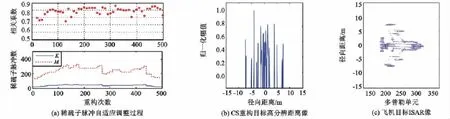
圖3 基于CS的認知雷達高分辨成像Fig.3 High－resolution imaging of cognitive radar based on CS

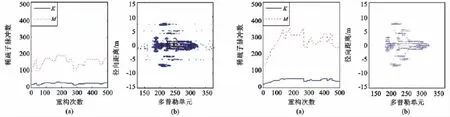
圖4 T2＝0.75時的認知雷達成像（M＝149）圖5 噪聲條件下的認知雷達成像（M＝283）Fig.4 Imaging of cognitive radar in T2 ＝0.75（M ＝149）Fig.5 Imaging of cognitive radar in noise environment（M ＝283）

表1給出了利用本文所提方法和傳統(tǒng)方法所得結(jié)果的比較。可以看出，為獲得成像所需的500個飛機目標的HRRP，通過本文方法，無論在高精度要求、低精度要求還是噪聲環(huán)境中，都能夠自適應地調(diào)整雷達信號波形，充分利用雷達頻譜資源。同時，通過本文方法成像還有效減少了系統(tǒng)運算時間，增強了雷達系統(tǒng)的實時處理能力。

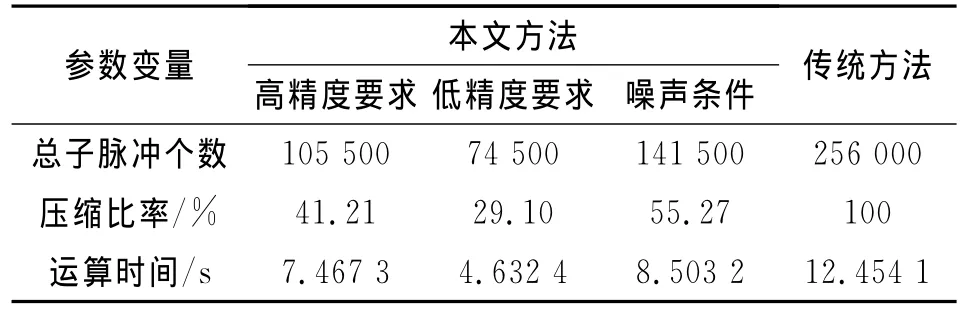
表1 系統(tǒng)性能比較Tab.1 Comparison of the system＇s capability

4 結(jié)論

本文結(jié)合認知雷達的信息反饋回路，提出了基于壓縮感知的認知雷達高分辨成像方法。該方法首先對成像目標稀疏度進行了大致估計，其次根據(jù)重構(gòu)得到的目標距離像之間的相關(guān)系數(shù)自適應地調(diào)整后續(xù)發(fā)射信號波形，逐步實現(xiàn)對目標距離向信息的認知，最后對重構(gòu)得到的各次高分辨距離像通過傳統(tǒng)方法進行壓縮，得到了目標的高分辨二維像。仿真表明：與傳統(tǒng)方法相比，本文所提方法充分利用了目標所處環(huán)境信息自適應調(diào)整發(fā)射信號波形，更具有智能化特點，且需要更短的系統(tǒng)運算時間，更適合于日益復雜的電磁環(huán)境。

［1］Haykin S.Cognitive radar：a way of the future［J］.IEEE Signal Processing Magazine，2006，23（1）：30－40.

［2］Goodman N A.Closed－loop radar with adaptively matched waveforms［C］／／2007International Conference on Electromagnetics in Advanced Applications.Torino，Italy，2007：468－471.

［3］范梅梅，廖東平，丁小峰，等.基于 WLS－TIR的多目標識別認知雷達波形自適應方法［J］.電子學報，2012，40（1）：73－77.FAN Meimei，LIAO Dongping，DING Xiaofeng，et al.A－daptive waveform design based on wls－tir for multiple targets recognition in cognitive radar［J］.Acta Electronica Sinica，2012，40（1）：73－77.

［4］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：1 289－1 306.

［5］Y S Yoon，M G Amin.Compressed sensing technique for high－resolution radar imaging［J］.Proceedings of SPIE，2008，6968（1A）：1－10.

［6］L Zhang，M D Xing，C W Qiu，J Li，J L Sheng，Y C Li，Z Bao.Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved Compressive Sensing［J］.IEEE Transactions on Geoscience and Remote Sensing，2010，48（10）：3 824－3 838.

［7］Michael Leisnering，Christian Debes，Abdelhak M.Zoubir.Compressive sensing in through－the－wall Imaging［C］／／International Waveform Diversity and Design Conference（WDD），2010：150－154.

［8］Candes E，Romberg J，Tao T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information［J］.IEEE Trans on Info Theory，2006，52（2）：489－509.

［9］Kunis S，Rauhut H.Random sampling of sparse trigonometric polynomials II：Orthogonal matching pursuit versus basis pursuit［J］.Foundations of Computational Mathematics，2007，8（6）：737－763.

［10］Ying Luo，Qun Zhang，Cheng－wei Qiu，Xian－jiao Liang，Kai－ming Li.Micro－Doppler effect analysis and feature extraction in ISAR imaging with stepped－frequency chirp signals［J］.IEEE Transactions on Geoscience and Remote Sensing，2010，48（4）：2087－2098.