電動伺服系統剛度問題研究

張兆凱，唐 苗，曹東海，謝勁松

( 1．北京自動化控制設備研究所，北京100074; 2．海軍駐航天科工三院軍事代表室，北京100074)

0 引 言

伺服系統承載負載力矩時輸出有時會有較大偏差，當負載擾動劇烈時，甚至會導致系統失穩等惡劣后果，該問題可歸結為系統伺服剛度不足。本文從工程應用中的實際問題出發，引述了伺服剛度的概念，建立了電動伺服系統的模型，分析了負載作用下影響伺服系統跟蹤誤差和穩定性的關鍵因素，闡述了提高系統伺服剛度的理論本質，提出了采用陷波器進行串聯校正處理，消除系統諧振、提高系統增益來提高伺服系統剛度的控制方法。仿真結果表明，陷波器能夠有效抑制系統諧振，從而能夠進一步提高系統增益，從而提高系統剛度。

1 電動伺服系統工程應用中的剛度問題總結

在電動伺服系統工程應用中，存在系統加負載后穩態誤差增大，不能滿足跟蹤精度要求，如圖1 所示，此時我們希望通過增大系統增益來降低系統穩態誤差，但是增大系統增益后系統出現振蕩，也不能滿足工程應用要求，如圖2 所示。這類問題發生時，通常產品已經生產完畢，通過有限的調試參數難以解決，系統控制品質大受影響，不能滿足工程需求。

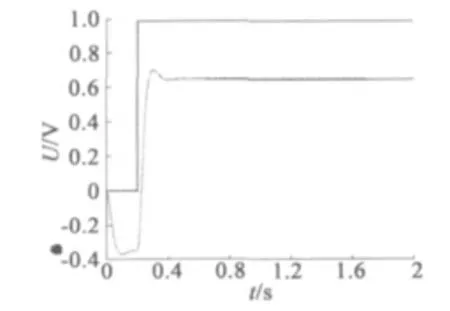
圖1 負載作用下系統穩態誤差增大示意圖

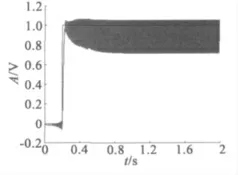
圖2 提高增益時系統自激振蕩響應示意圖

從動力學角度分析，可以將這種問題歸結為伺服系統的伺服剛度不足。

2 伺服系統剛度概念

伺服剛度是指整個伺服系統表現出來的抵抗外部擾動力矩產生位移偏差的能力。對比上述問題，我們希望在外加負載作用下，系統穩定并且輸出與期望值越小越好，即要求系統伺服剛度高。設外加負載力矩為Fs，由負載力矩引起的輸出軸轉角位置偏差為Δθ，則伺服系統的剛度Kservo定義:

式中: 當Fs為靜力矩，即恒定的外加負載時，Kservo稱為靜剛度; 當Fs為交變力矩時，Kservo稱為動剛度。

按照式( 1) 定義，Fs越大，Δθ 越小，則Kservo越大。Δθ 是系統空載和負載作用下系統穩態響應的差值，從控制理論角度看，如果在相同的負載作用下，伺服系統響應的穩態跟蹤誤差越小，則其Δθ 通常也會減小，則系統伺服剛度就高。

因此可以將提高系統伺服剛度的理論本質歸結為: 提高伺服剛度，即是抑制系統振蕩等不穩定因素，提高系統穩定裕度，減小系統在外加負載Fs作用下的穩態跟蹤誤差。

對于可簡化為二階系統的伺服系統來說，減小系統跟蹤誤差，需要提高系統增益; 然而提高系統增益，有時帶來系統振蕩等后果。因此，無法單純依靠提高系統增益的方式提高系統伺服剛度。需要從系統模型入手，詳細分析負載作用下系統響應特性，確定問題的關鍵因素，找到一個既能減小跟蹤誤差，又可以抑制系統振蕩，提高穩定裕度的方法。

3 電動伺服系統模型建立

假設電動伺服系統位置反饋傳感器安裝在輸出軸末端，即所有的環節都含在控制閉環內，電動伺服系統框圖模型如圖3 所示。

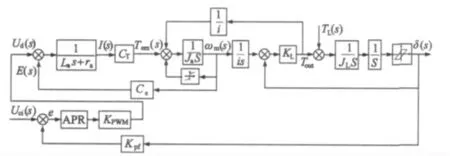
圖3 電動伺服系統框圖模型

圖中，Uci為輸入信號，TL為外加負載力矩，δ 為輸出偏轉角，APR 為控制器，Kpwm為功率放大倍數，La為電機電樞電感，Ra為電機電樞電阻，CT為電機力矩系數，Ce為電機反電動勢系數，Kpf為位置反饋系數，Ja為電機轉動慣量，i 為減速比，KL為傳動機構結構柔性系數，JL為負載轉動慣量。

由圖3 看出，系統模型為一個二質量體扭轉模型，也可作為一個雙輸入單輸出系統，分析系統剛度，即分析外界負載力矩TL變化造成的輸出偏轉角δ 的變化，系統剛度越高，輸出偏轉角δ 受外界負載力矩TL的影響越小。

4 系統響應特性分析

4.1 常值負載作用下系統響應對比分析

以某型電動伺服系統為例，代入模型參數，進行常值負載作用下系統時域響應仿真。圖4 給出了10 N·m 外部負載力矩狀態下，結構柔性系數KL分別為109N·m/( °) 、107N·m/( °) 、3 × 104N·m/( °) 時系統階躍響應仿真圖。從圖中看到，KL為3× 104N·m/( °) 時，系統已經振蕩失穩; KL為109N·m/( °) 、107N·m/( °) 時，系統宏觀響應穩態誤差和響應時間均相同。

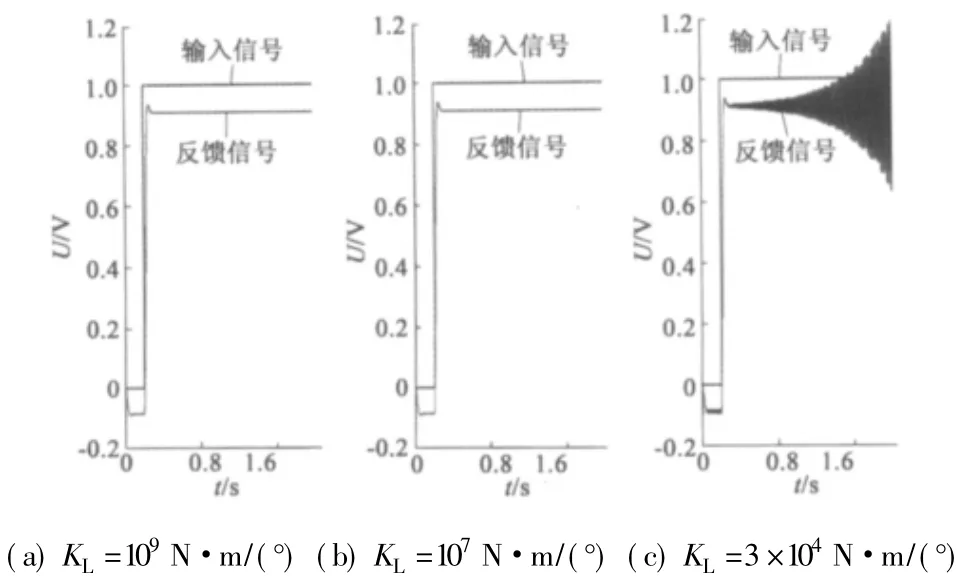
圖4 恒定負載，結構柔性系數K L 變化時階躍響應宏觀對比圖

圖5 給出了KL為109N·m/( °) 、107N·m/( °) 系統穩態時響應曲線放大示意圖。從圖中看出，KL為109N·m/( °) 時，反饋振蕩幅值約0．000 4 V，頻率約24 600 Hz，KL為107N·m/( °) 時，反饋振蕩幅值約0．000 7 V，頻率約2 450 Hz，但是振蕩曲線中心幅值基本相同。

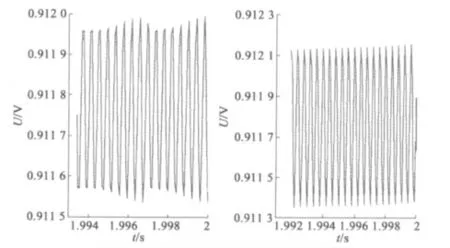
圖5 圖4 中穩態響應局部放大圖

在模型中固定KL為107N·m/( °) ，負載力矩值為10 N·m、30 N·m、50 N·m 時系統階躍響應和穩態時響應曲線放大圖如圖6 和圖7 所示。

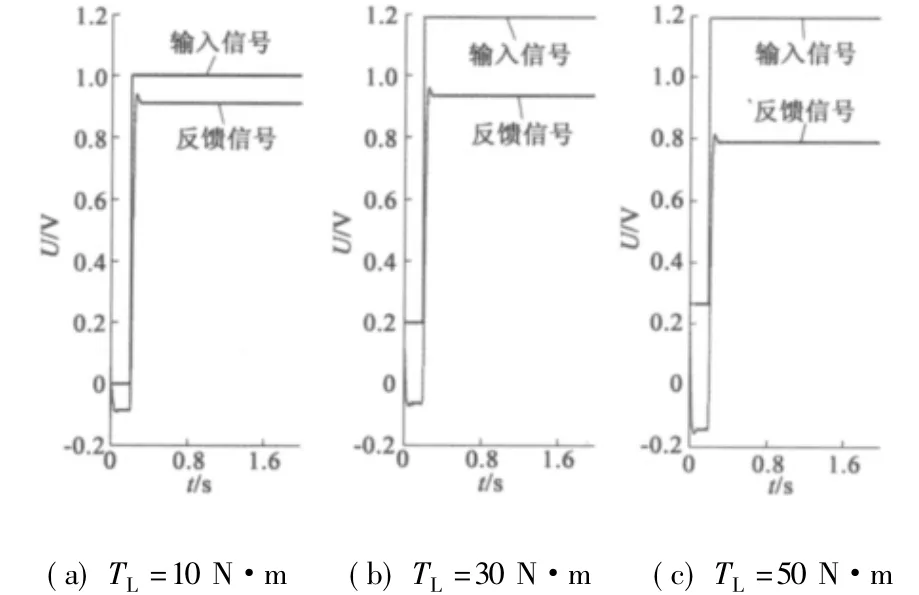
圖6 結構柔性系數K L 恒定，負載值變化時階躍響應對比圖

從圖6 和圖7 中看到，KL為107N·m/( °) 時，系統宏觀上能夠穩定跟蹤輸入階躍信號，但是隨著負載力矩增大，穩態誤差加大，但響應中疊加的高頻振蕩幅值和頻率沒有改變。

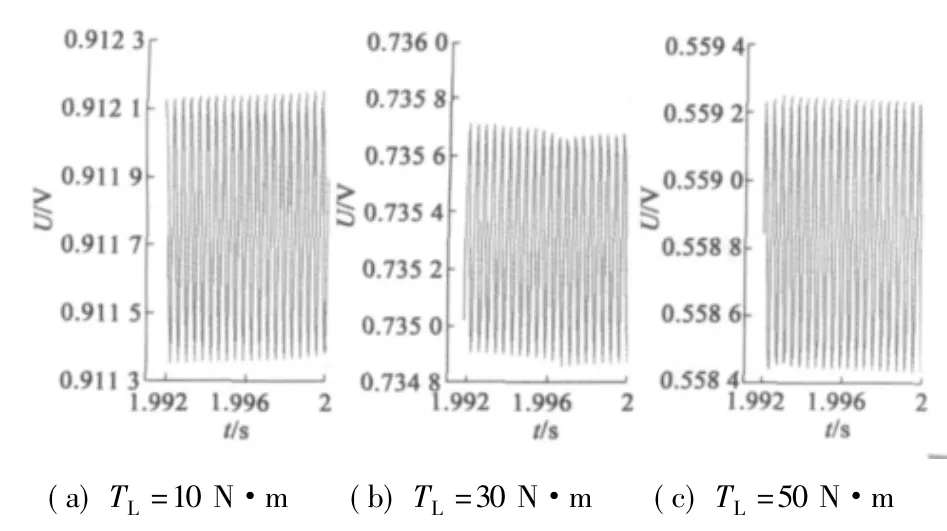
圖7 圖6 中穩態響應局部放大圖

由以上仿真可以看出，在伺服系統參數一定、響應穩定的狀態下，伺服系統跟蹤誤差只隨負載力矩大小改變，系統響應中疊加的高頻振蕩成份由傳動機構的結構柔性決定，結構柔性不影響系統穩態誤差。傳動機構結構柔性小時，伺服系統可以穩定跟蹤輸入階躍信號，隨著負載力矩增大，系統穩態誤差增大; 在相同負載力矩作用下，當結構柔性增大時，系統穩態誤差不會因柔性增大而減小，根據伺服剛度定義，可以認為系統靜伺服剛度不受影響; 但是伺服系統宏觀出現自激振蕩的風險加大，穩定裕度降低; 當結構柔性增大到一定程度，系統宏觀響應上會出現自激振蕩，系統不能穩定跟蹤輸入信號，從伺服剛度定義看，此時系統靜伺服剛度為零。

4.2 交變負載作用下系統響應對比分析

在模型中施加幅值為30 N·m，頻率為200 Hz的交變負載力矩，設置KL分別為109N·m/( °) 、107N·m/( °) 、105N·m/( °) ，仿真所得系統階躍響應穩態時曲線局部放大如圖8 所示。從圖中看到，KL分別為109N·m/( °) 、107N·m/( °) 時，系統階躍響應穩態時幅值波動頻率與力矩交變頻率相同，響應中疊加高頻振蕩，響應幅值波動約為0．001 5 V; 當KL為105N·m/( °) 時，系統處于諧振狀態，振蕩幅值約0. 01 V。

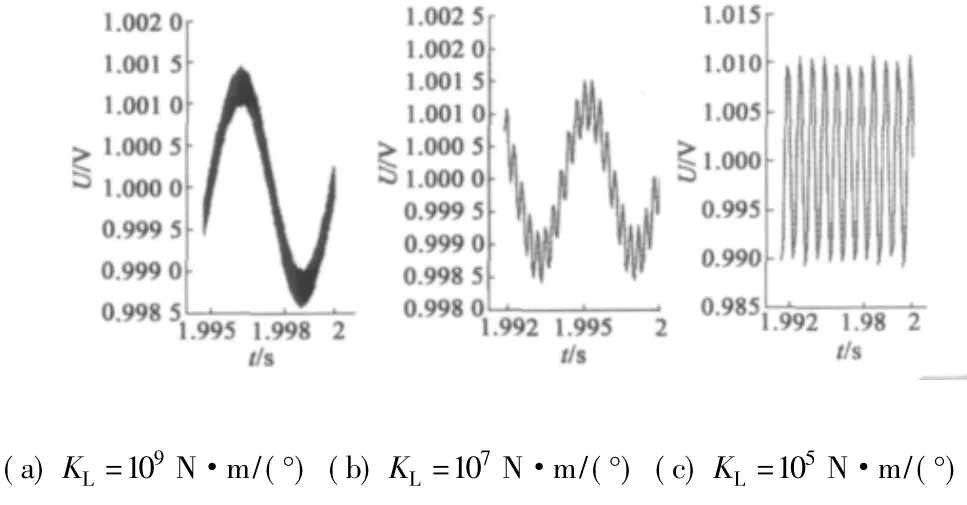
圖8 交變負載，結構柔性系數K L 變化時系統階躍響應穩態局部放大對比圖

在模型中設KL為107N·m/( °) ，施加200 Hz，幅值分別為10 N·m、30 N·m、50 N·m 交變負載，系統響應如圖9a 所示; 施加2 450 Hz，幅值分別為10 N·m、30 N·m、50 N·m 交變負載，系統響應如圖9b 所示。

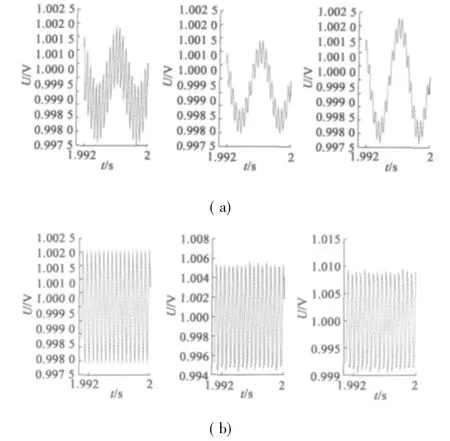
圖9 結構柔性系數K L 固定，交變負載變化系統階躍響應穩態局部放大對比圖

從以上仿真結果可知，系統在不發生諧振的狀態下，系統階躍響應穩態時幅值波動只隨負載幅值增大而增大，系統響應中疊加的高頻振蕩成份由傳動機構的結構柔性決定，結構柔性不影響因負載力矩造成的響應波動幅值; 這與施加常值負載時穩態誤差隨負載增大而增大結論是一致的，此時可以認為系統動伺服剛度不受結構柔性影響。當系統諧振時，系統響應振蕩幅值均大于穩定狀態下因負載力矩引起的波動值，并且諧振狀態下，施加負載力矩幅值越大，振蕩幅值也越大，系統諧振為不穩定狀態，因此可以認為此時系統動伺服剛度為零。

4.3 小結

綜上，不論施加常值負載還是交變負載，在系統響應不發生諧振的狀態下，負載大小決定了系統跟蹤誤差，負載越大，跟蹤誤差越大; 當系統發生自激振蕩或諧振時，系統振蕩幅值遠大于穩定狀態下系統因負載引起的跟蹤誤差。在系統穩定響應的狀態下，結構柔性不影響系統的伺服剛度，但是系統一旦振蕩不穩定，按照定義，系統伺服剛度就是零; 而決定系統是否發生諧振或自激振蕩的一個關鍵因素是傳動機構的結構柔性，結構柔性越大，系統振蕩風險越大。

4.4 頻域分析

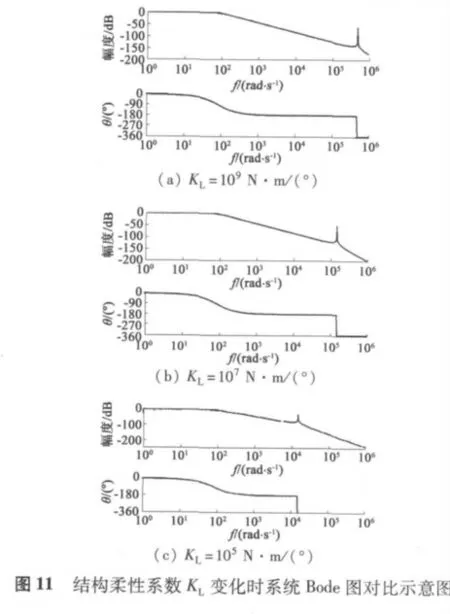
為了進一步明確系統內部影響其穩定裕度，造成響應振蕩的關鍵因素，對系統進行頻域分析。圖10 給出了KL為無窮大和KL為有限值的Bode 圖對比。圖11 給出了變化結構柔性系數KL大小時系統Bode 圖的變化規律。

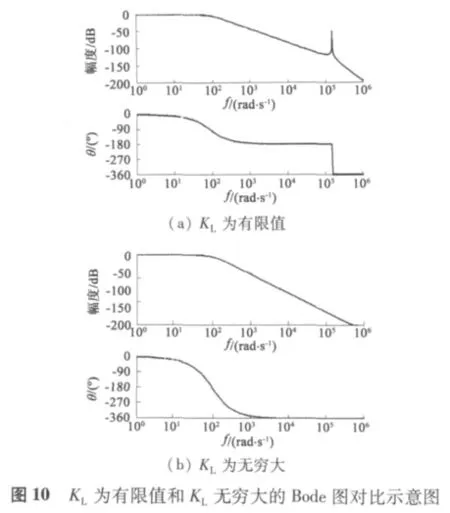
從圖10 中看到，KL為有限值時，由于結構柔性的影響，使得系統高頻段存在諧振峰，諧振點處相角滯后在180°左右，這意味著系統響應中存在有自激振蕩情況，振蕩頻率約為諧振峰頻率點頻率。在正常情況下，我們在系統響應中看不到諧振現象是因為諧振幅值很小，在宏觀上觀察不到。從圖11 中看到，隨著KL減小，即結構柔性系數增大時，諧振頻率點左移，幅值響應也逐漸增大，系統響應宏觀上出現諧振的風險加大。這與上述時域分析結果一致。同時因為諧振峰的存在，如果為了減小系統跟蹤誤差而提高增益，則系統很容易發生振蕩而不穩定。因此無法通過提高增益的方式來達到提高系統伺服剛度的目的。

5 使用陷波器提高系統剛度

從上述分析來看，無法提高系統增益來提高伺服剛度是因為系統中存在傳動機構的結構柔性因素引起的諧振峰。雖然，可以通過重新改進傳動機構等方式減小傳動機構的結構柔性，但是有時對工程應用來說代價太高。從控制理論角度看，控制系統是一個開放的系統，我們也可以通過補償、校正等手段削弱系統的諧振，提高系統穩定性，從而進一步提高系統增益，提高系統剛度。

在以上模型中，針對諧振點頻率，在控制器APR 中設計串聯陷波器如下:

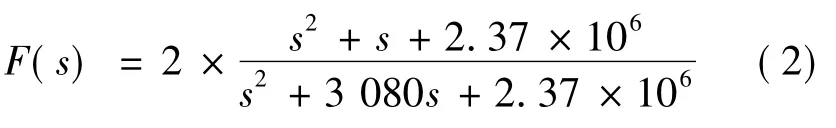
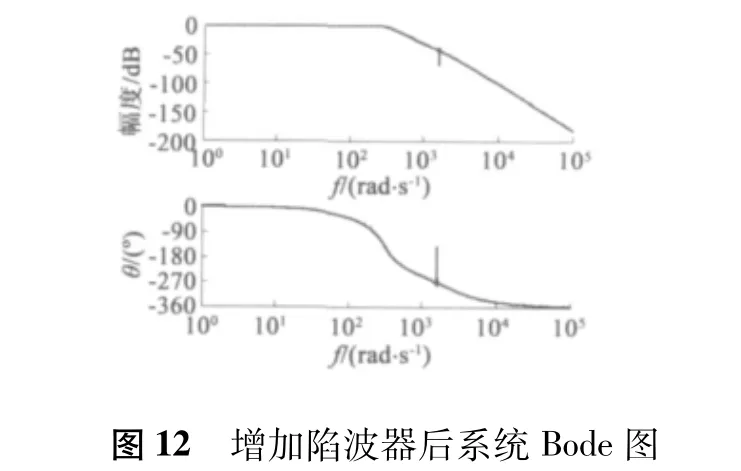
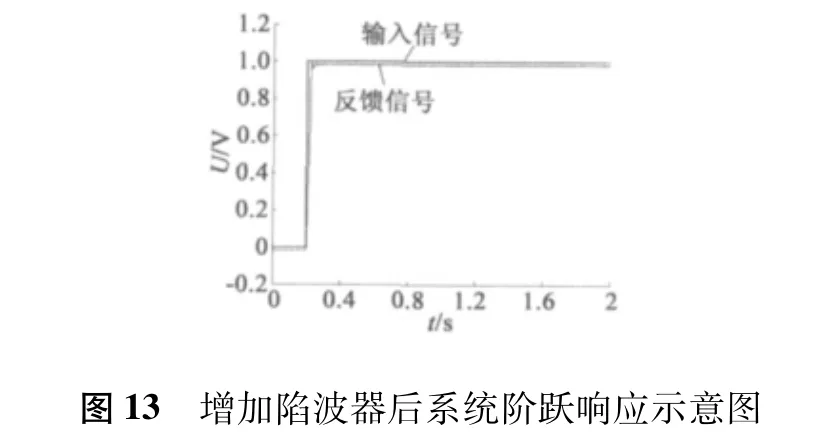
所設計的陷波器增益為2，中心頻率點與系統諧振頻率點對應，增加陷波器后，系統Bode 圖如圖12 所示。50 N·m 負載作用下，系統階躍響應如圖13 所示。從圖中看到，陷波器有效抑制了系統諧振峰，使系統響應穩定跟蹤輸入，并且陷波器增益為2，使原系統增益擴大了1 倍，系統跟蹤穩態誤差明顯減小，系統伺服剛度得到有效提高。

6 結 語

電動伺服系統工程應用中希望伺服剛度高，從控制理論分析，問題本質就是在負載作用下保持系統穩定，減小跟蹤誤差。本文提出了采用陷波器抑制傳動機構結構柔性帶來的系統諧振峰，提高系統增益來提高系統伺服剛度的方法，仿真結果分析表明，陷波器能夠有效抑制系統諧振，提高系統增益，減小跟蹤誤差，即有效提高了系統伺服剛度。

［1］ 張盛楠．電動伺服系統非線性建模、仿真與測試技術［D］．北京自動化控制設備研究所，2012．

［2］ 寇寶泉．交流伺服電機及其控制［M］．北京: 機械工業出版社，2008．

［3］ 郭慶鼎．現代永磁電動機交流伺服系統［M］．北京: 中國電力出版社，2006．

［4］ 劉剛．永磁無刷直流電機控制技術與應用［M］．北京: 機械工業出版社，2008．