基于因子分析法的滑坡變形分析

張婷婷，晏鄂川，胡顯明，范彬彬

(中國地質大學(武漢)工程學院，武漢 430074)

1 研究背景

滑坡的位移監測成果是認識滑坡機理、演化過程及其預測預報的基本信息。然而，由于滑坡類型的多樣性以及演變規律的復雜性，加之各種影響因子的綜合作用，使得滑坡變形表現出復雜特性。因此，面對復雜的監測信息，需通過某種數學分析方法對因子進行分析，獲得我們所需要的滑坡變形信息。

目前，關于位移監測資料的分析處理理論或方法很多，如灰色系統理論、人工神經網絡、時間序列分析、支持向量機等［1－3］。這些理論主要是根據監測的歷史位移信息預測(或計算)滑坡未來某個時間段的位移信息，但未對監測資料從演化系統的角度進行處理，因此，降低了滑坡變形分析結果的可信性與實用性。

因子分析的基本目的就是用少數幾個因子去描述許多指標或因素之間的聯系，即將相關比較密切的幾個變量歸在同一類中，每一類變量就成為一個因子(之所以稱其為因子，是因為它是不可觀測的，即不是具體的變量)，以較少的幾個因子反映原始資料的大部分信息，同時這幾個少數因子之間又是相互獨立的。運用這種研究方法，以滑坡位移監測資料為研究對象，我們可以找出影響位移變化的主要因素，以及它們的影響力(權重)，既合理地解釋了包含在因子之間的相關性，又簡化了觀測系統，抓住了影響所有觀測數據的主要矛盾。

因子分析最早于1904年由C.斯皮爾曼在研究心理學時提出，上世紀50年代開始在氣象學、醫學、考古學、經濟學、社會學和地質學等領域中得到廣泛應用［4－9］，但在工程領域巖土體穩定性的分析與評價中應用較少［10－11］。因此，本文將因子分析法用于滑坡位移監測資料的分析與處理，在滑坡變形公共因子分析基礎上，揭示滑坡機理，進行滑坡變形狀態分析。

2 因子分析法原理

因子分析是降維分析，降維后使變量或標本更具明確的實際意義。因子分析可分Q型和R型。Q型因子分析是對標本(樣品)進行成因分類和系統分類;R型因子分析則是研究變量之間的關系。本文以滑坡9個地表位移監測點為變量，采用R型因子分析。

2.1 因子分析的數學模型［12］

因子分析最簡單的數學模型為線性模型。根據變量X的相關矩陣，可把原來的p個變量表示成若干個因子(新變量)的線性組合的形式，其矩陣形式為

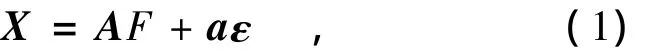
具體表達式為:

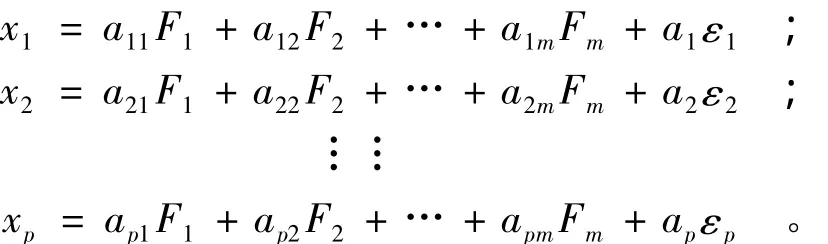
式中:F1，F2，…，Fm叫做公共因子，它們是在各個變量中都共同出現的因子，彼此相互獨立，可以把它們理解為在高維空間中的相互垂直的m個坐標軸。

ε1，ε2，…，εp叫做特殊因子，是單一變量所特有的因子，各特殊因子間以及特殊因子與所有公共因子間都是相互獨立的。

aij叫做因子荷載，是第i個變量在第j個公共因子上的負荷，矩陣因子載荷矩陣。

ai為特殊因子εi的因子系數，或者叫做特殊因子載荷。

2.2 因子求解

在進行求解時，將原始數據標準化，使其平均數為0，方差為1。采用主成分法進行因子求解，其求解式為

式中:αi(i=1，2，…，p)為相關矩陣中提取的特征值λj(j=1，2，…，m)所對應的特征向量，是單位向量;第j個特征值的平方根，是一個權，用來表示因子的重要性。

因子模型中的統計量包括因子載荷、變量共同度及公共因子方差貢獻，其統計意義如下:

(1)因子載荷aij表示第i個變量和第j個公共因子的相關系數。

(3)公共因子方差貢獻Sj是因子載荷矩陣中各列元素的平方和，它是指同一公共因子Fj對諸變量所產生的方差之總和，用來衡量該公共因子的重要性。

3 應用研究

3.1 滑坡地質概況

三峽庫區某土質滑坡，滑坡滑體主要由碎塊石夾粉質黏土組成，前部和后部較薄，中部厚度較大，約10～40 m。碎塊石成分主要來源于T2b3泥灰巖、灰巖，碎石粒徑一般5～10cm，塊石一般大于50cm，土石比4∶6，結構較為松散，滲透性較強。滑帶物質成分主要為含礫粉質黏土，厚30～200cm。滑床為由T2b2泥紫紅色粉砂質泥巖組成，巖層產狀220°∠35°。

滑坡后緣高程300 m，前緣涉水。滑坡縱長450 m，寬240 m，平均厚度20 m，總面積10.8×104m2，總體積216×104m3。滑坡平面形態呈長舌形，總體坡向193°，后窄前寬。剖面形態呈凸形，后緣處呈圈椅狀，后緣壁為高1～3 m陡坎。滑坡的東西兩側以沖溝為界，沖溝寬20～30 m，切深10～15 m。滑坡監測點布置及剖面圖如1、圖2。

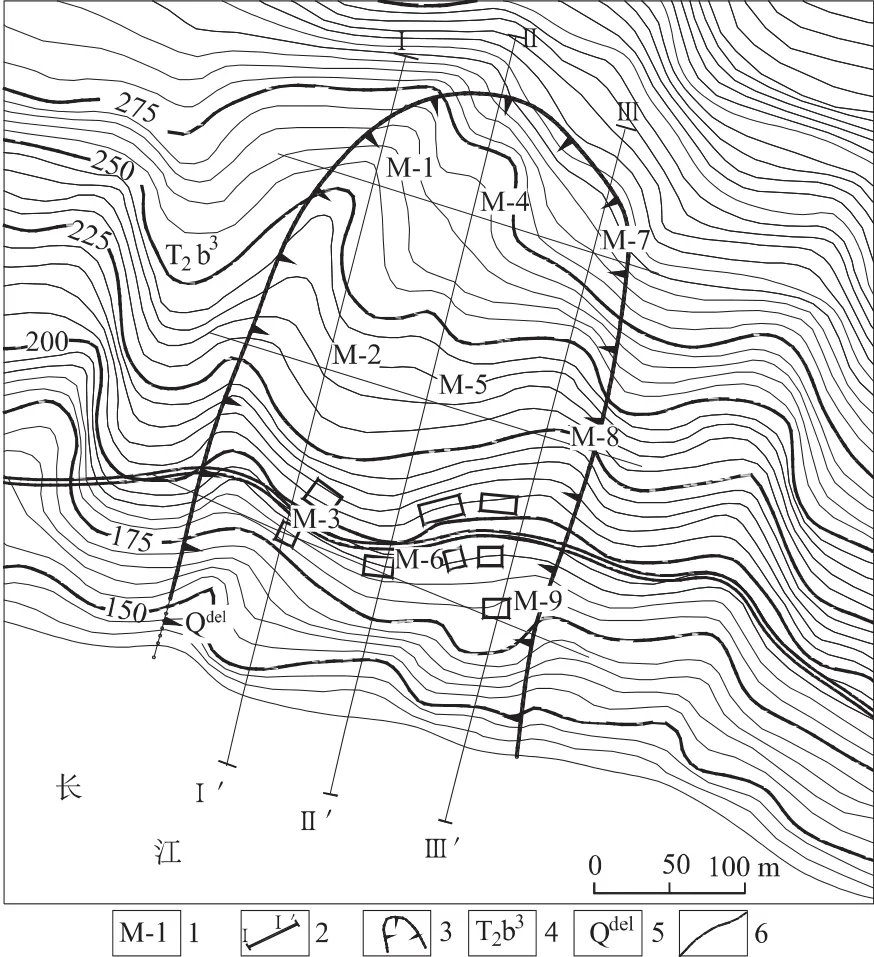
圖1 滑坡監測點平面布置Fig.1 The distribution of monitoring points on the landslide

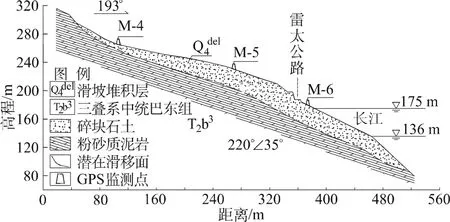
圖2 滑坡工程地質主剖面Fig.2 The main geological profile of the landslide

3.2 滑坡位移的因子分析

選取2008年10月至2009年9月(1個水文年)內的月位移量進行R型因子分析，取9個地表位移監測點為變量，求得其相關系數矩陣，并運用式(2)求得其因子解，得到因子載荷矩陣見表1。

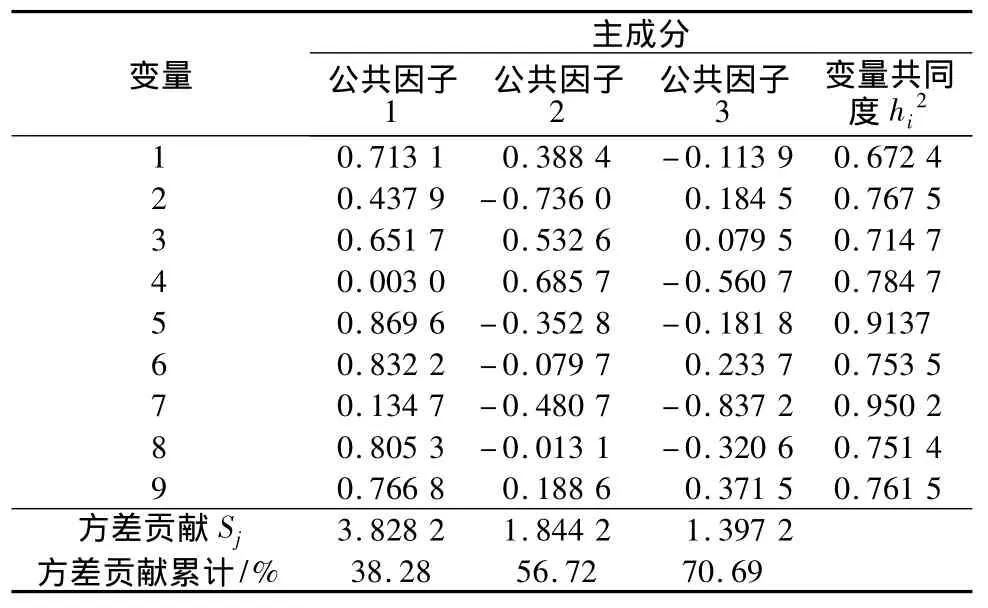
表1 因子載荷矩陣Table 1 Factor loading matrix

為了更加明確這3個公共因子的實際意義，通過因子模型的幾何意義進行解釋，將各變量的因子荷載在每個公共因子軸(坐標軸F1，F2，F3分別代表公共因子1，2，3)上的分布顯示如圖3，各個變量的因子荷載絕對值均小于1，圖中的數字為變量(監測點)。另外，圖中標出了監測點在滑坡中的位置(前、中、后分別代表滑坡前緣、中部、后緣)，其中監測點1—3位于滑坡右側區的剖面，監測點4—6位于滑坡主剖面，監測點7—9位于滑坡左側的剖面。

從圖3中的因子荷載分布圖可知，圖(a)、(b)的因子載荷分布有一定的集中趨勢。從圖3(a)可以看出，在公共因子1上投影較大的變量監測點主要位于滑坡的前緣和中部，結合實際情況，庫水作用對滑坡中前部變形的影響比較明顯，因此可以認為公共因子1為庫水因子，除此之外，對滑坡變形影響比較明顯的外部作用為降雨，因此可以認為公共因子2為降雨作用。另外，滑坡位移還與監測點所處的微地貌形態有關，因此可以認為公共因子3為監測點所在地形，這一點可從監測點3，6和9上的因子載荷較大，且位于滑坡前緣，而前緣地形較陡得到驗證。由上可知，庫水作用是影響該滑坡變形的最主要因素。

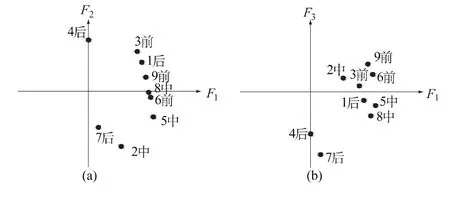
圖3 各變量公共因子載荷分布Fig.3 Factor loading distribution of each common factor

求得了因子荷載以后，將其乘以原始變量中的位移，可以得到各個公共因子在樣品(監測時間)內的位移量，由于該滑坡受庫水作用的影響較大，故將庫水因子(公共因子1)下的位移量列于表2。

從表中可以看出:庫水對位于滑坡后部的監測點4和7影響較小，其在各個月份內的位移量較小，對滑坡中前部的監測點3，5，6，8和9影響較大，位移量較大，尤其是位于主剖面上中前部的監測點5和6。另外，通過現場調查發現，該滑坡前緣存在明顯的局部變形破壞，變形區主要受長江水位的影響，滑坡前緣在庫水波動下，出現坍塌等破壞，然后牽引誘發滑坡出現前部變形。這一點與因子分析的結果是一致的。

同時，根據因子分析得到的最主要公共因子的位移量，可以對滑坡進行變形分區，指導滑坡的監測，對變形較大的部位應增加監測點，加大監測頻率。

4 滑坡變形機理分析

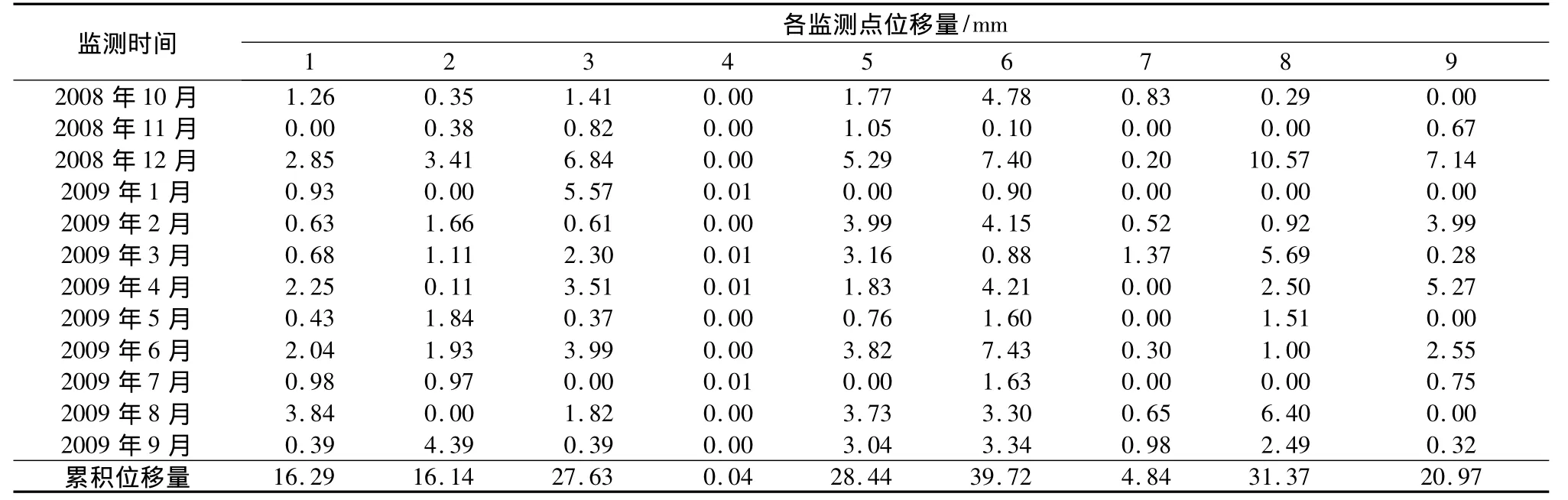
表2 庫水因子作用下的位移量Table 2 Displacements under the influence of reservoir water factor

由于庫水因子為主要影響因素，該滑坡屬于庫水型滑坡，庫水的變動引起了滑坡的主要變形，因此將庫水作用下的位移量分離出來，分析滑坡變形中庫水作用程度。根據表2，對位于滑坡主剖面上且位移量最大的監測點5和6做累積位移曲線圖(圖4)。從圖中可以看出，在1個水位年內，隨著庫水位的上升和下降，滑坡累積位移幾乎呈等斜率增加。

由于滑體所受的靜水壓力等效于其所受的浮托力和滲透力的合力［13］，因此從后者對庫水作用進行分析。庫水變動使滑體內產生浮托力和滲透力，一般而言，庫水上升過程中，浮托力產生的浮托減重效應減小了抗滑力，對滑體的穩定不利;庫水下降過程中，滲透力產生的滲透壓力效應增大了下滑力，對滑體穩定不利。對于不同類型的滑坡，這兩種作用在滑體中的作用程度不同，滲透性較好的滑坡，浮托減重效應較明顯，此類滑坡在庫水上升過程中的位移較明顯，稱之為浮托減重型滑坡;滲透性較差的滑坡，滲透壓力效應較明顯，此類滑坡在庫水下降過程中的位移變化較大，稱之為滲透壓力型滑坡;對于兩種作用都較明顯的滑坡，稱為復合型滑坡。

本文研究的滑坡即為復合型滑坡，這一點也可以從表2中的月位移量看出，監測點5和6均在2008年12月和2009年6月內的位移量較大，從圖4可知，這2個月份是庫水陡增和驟降的月份，說明庫水上升和下降對滑坡的變形均產生了重要影響。

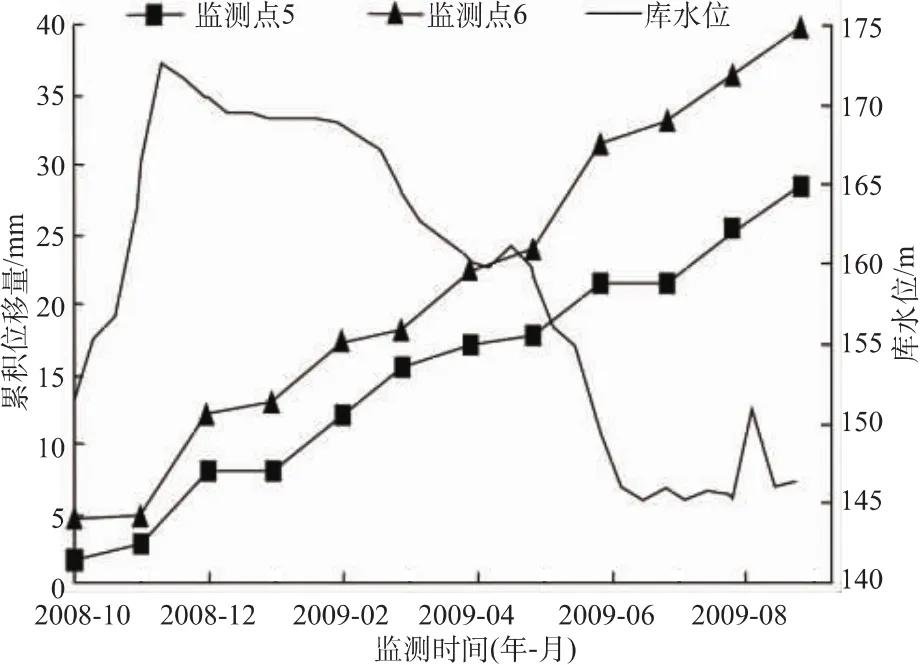
圖4 庫水因子作用下監測點5和6累積位移量Fig.4 Cumulative displacements at monitoring point 5 and 6 under the influence of reservoir water factor

5 結論

(1)通過因子分析得到了位移監測資料的公共因子有3個:其中公共因子1為庫水作用，是影響滑坡的主要因素，公共因子2反映的是降雨作用，是次要因素;公共因子反映了監測點所在的地形，為第3影響程度的因素。

(2)通過滑坡現場調查，該滑坡前緣存在明顯的局部變形破壞，變形區主要受長江水位的影響，滑坡前緣在庫水波動下，出現坍塌等破壞，然后牽引誘發滑坡現有變形區的出現。這一點與因子分析的結果一致。

(3)通過因子載荷計算了庫水因子作用下的位移量，分析了滑坡主剖面上的監測點5和6在庫水作用下的累積位移，幾乎呈等斜率直線增加。此外，監測點月位移量較大的月份為2008年12月和2009年6月，正好是庫水陡增和驟降的月份，因此庫水上升和下降對滑坡的變形均產生了重要影響，該滑坡為復合型滑坡。

［1］劉 曉，唐輝明，劉 瑜.基于集對分析和模糊馬爾可夫鏈的滑坡變形預測新方法研究［J］.巖土力學，2009，30(11):3399－3405.(LIU Xiao，TANG Huiming，LIU Yu.A New Model for Landslide Displacement Prediction Based on Set Pair Analysis and Fuzzy-Markov Chain［J］.Rock and Soil Mechanics，2009，30(11):3399－3405.(in Chinese))

［2］尹光志，張衛中，張東明，等.基于指數平滑法與回歸分析相結合的滑坡預測［J］.巖土力學，2007，28(8):1275－1278.(YIN Guang-zhi，ZHANG Weizhong，ZHANG Dong-ming，et al.Forecasting of Landslide Displacement Based on Exponential Smoothing and Nonlinear Regression Analysis［J］.Rock and Soil Mechanics，2007，28(8):1275－1278.(in Chinese))

［3］高 瑋，馮夏庭.基于灰色-進化神經網絡的滑坡變形預測研究［J］.巖土力學，2004，25(4):514－517.(GAO Wei，FENGXia-ting.Study on Displacement Prediction of Landslide Based on Grey System and Evolutionary Neural Network［J］.Rock and Soil Mechanics，2004，25(4):514－517.(in Chinese))

［4］XIONG G Y，VIRASAKDI C，GEATER A，et al.Factor Analysis on Symptoms and Signs of Chronic Low-Back Pain Based on Traditional Chinese Medicine Theory［J］.Journal of Alternative and Complementary Medicine，2011，17(1):51－55.

［5］CAI L.A Two-Tier Full-Information Item Factor Analysis Model with Applications［J］.Psychometrika，2010，75(4):581－612.

［6］KIM H J.Common Factor Analysis Versus Principal Component Analysis:Choice for Symptom Cluster Research［J］.Asian Nursing Research，2008，2(1):17－24.

［7］WANG SL，WANG J，CHEN H W，et al.The Classification of Tumor Using Gene Expression Profile Based on Support Vector Machines and Factor Analysis［C］∥IEEE Computer Society.The 6th International Conference on Intelligent Systems Design and Applications(ISDA 2006)，Ji’nan，China，Oct 15－18，2006，(2):471－476.

［8］JIANGR，FU WY，WANGJM，et al.Efficient Statistical Capacitance Variability Modeling with Orthogonal Principle Factor Analysis［C］∥IEEE/ACM International Conference on Computer Aided Design.California，USA，November，06－10，2005:683－690.

［9］FUNG W K，KWAN C W.Identifying Influential Observations for Loadings in Factor Analysis［C］∥Psychometric Society.New Developments in Psychometrics:Proceedings of the International Meeting of the Psychometric Society IMPS2001，Osaka，Japan，2003:165－172.

［10］馬水山，王志旺，張 漫.滑坡監測資料的因子分析［J］.巖石力學與工程學報，2002，21(7):1003－1006.(MA Shui-shan，WANG Zhi-wang，ZHANG Man.Factor Analysis on Monitoring Data of Landslide［J］.Chinese Journal of Rock Mechanics and Engineering，2002，21(7):1003－1006.(in Chinese))

［11］趙鵬大，胡旺亮，李紫金.礦床統計預測［M］.北京:地質出版社，1983:217－234.(ZHAO Peng-da，HU Wang-liang，LI Zi-jin.Statistical Prediction of Mineral Deposit［M］.Beijing:Geological Press，1983:217－234.(in Chinese))

［12］王學仁.地質數據的多變量統計分析［M］.北京:科學出版社，1982:249－296.(WANGXue-ren.Multivariable Statistical Analysis of Geological Data［M］.Beijing:Science Press，1982:249－296.(in Chinese))

［13］毛昶熙，段祥寶.關于滲流的力及其應用［J］.巖土力學，2009，(30):1569－1574.(MAO Chang-xi，DUAN Xiang-bao.On Seepage Forces and Application［J］.Rock and Soil Mechanics，2009，(30):1569－1574.(in Chinese ))