應用目標全息反饋和ESO的勵磁控制器設計

常家寧， 贠旭明， 于紫南， 謝國強

(1.重慶市電力公司長壽供電局， 重慶 401220；2.中國水電崇信發電有限責任公司物資部， 平涼 744200；3.吉林省電力公司吉林供電公司， 吉林 132012； 4.江西省電力科學研究院， 南昌 330000)

應用目標全息反饋和ESO的勵磁控制器設計

常家寧1， 贠旭明2， 于紫南3， 謝國強4

(1.重慶市電力公司長壽供電局， 重慶 401220；2.中國水電崇信發電有限責任公司物資部， 平涼 744200；3.吉林省電力公司吉林供電公司， 吉林 132012； 4.江西省電力科學研究院， 南昌 330000)

為了改善發電機勵磁控制器的性能，應用目標全息反饋將仿射非線性系統方程中的非線性因素轉換到含有控制輸入的狀態方程中，并得到對應的Brunovsky標準型。由于轉換后的系統中非線性因素都包含在虛擬控制輸入的方程中，可以通過構造二階的ESO來觀測系統中未知擾動并將其反饋線性化，進而得到線性模型。然后使用極點配置法來求得系統的線性部分的反饋增益系數。為驗證文中方法的有效性，在MATLAB上進行仿真試驗，仿真結果證明了該方法的可行性。

勵磁控制； 目標全息反饋； 擴張狀態觀測器； 極點配置； 布魯克斯標準型

勵磁控制系統是電力系統的重要組成部分，其設計方法一直以來備受人們的重視。在這些設計方法中，微分幾何理論作為一種嚴謹的數學理論能將仿射非線性系統轉化為Brunovsky標準型，從而為精確線性化提供了有利的條件。文獻[1～5]分別從不同方向證明了微分幾何理論在不同系統的控制器中的有效性。但基于微分幾何理論的設計方法中控制目標的選取需滿足特定的條件，因此其控制目標選取會受到一定的約束，致使部分關心的控制目標的控制性能無法滿足系統運行要求[6]。文獻[7]提出了目標全息反饋法，將系統運行時比較關心的發電機電磁功率、機端電壓和角速度作為狀態變量將其置于Brunovsky標準型中，克服了狀態變量無法靈活選取的缺點。文獻[8]的結果證明了目標全息反饋法的有效性。

另外，直接基于微分幾何理論的反饋線性化要求完整和準確的系統模型和參數，一旦系統發生擾動或含有未建模部分時，將會對系統的穩定性產生一定的影響。因此，需要一種能夠準確估計并實時反饋的觀測器對直接基于微分幾何理論的反饋線性化方法進行必要的補充。文獻[9]提出的擴張狀態觀測器ESO(extended state observer)正是能夠滿足實時跟蹤和補償的理想觀測器。文獻[10]比較了比例積分微分PID(proportion integration differentiation)控制、H2/H∞控制、精確反饋線性化方法、自抗擾控制和基于ESO的非線性魯棒控制的優缺點，并說明帶有ESO的控制器者具有較好的自適應性，為基于ESO的控制方法的應用提供了理論依據。文獻[11]將ESO和滑模變結構控制器結合起來應用無刷直流電機BLDCM(brushless direct current motor )的控制，并取得了較為理想的的結果。文獻[12]將基于ESO的魯棒控制應用于勵磁和靜止移相器的聯合控制，證明了該法具有一定的現實可行性。

本文通過目標全息反饋法選取適當變量組成新狀態方程，即轉化為含有新狀態變量的Brunovsky標準型，然后構造二階的ESO來消除擾動變量，得線性狀態方程組，并通過極點配置法得線性部分狀態反饋的表達式，最后仿真結果驗證了該方法。

1 單機無窮大系統數學模型

發電機單機無窮大系統的三階模型為

(1)

(2)

Utd=xqUssinδ/xqΣ

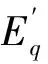
2 目標全息反饋法

對于如下的單輸入非線性控制系統：

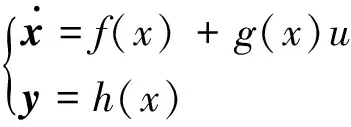
(3)

式中：x為系統n維狀態變量，是關于x可微非線性向量場；y=h(x)為m維輸出向量；u為控制變量。

如果y是式(3)輸出量期望跟蹤的目標，則可以得到多目標方程為

ei=yi-yir(i=1，2，…，m)

(4)

要想解決式(3)所表示系統的多目標跟蹤問題，在多目標方程式(4)中，尋找某輸出量yi與式(1)具有一階關系度，并把該量標記為ym，于是有

(5)

綜合式(4)和(5)，可以得到下面的方程：

(6)

3 擴張狀態觀測器

對式(6)所對應形式的狀態方程組，因為所有的非線性因素被包含在最后一個方程中，所以構造ESO時可以只考慮它，構造的ESO階數僅比它高一階即可。所以構造對應的二階ESO，形式如：

(7)

其中：w1為em估計值；w2為擴張變量，用于估計變量

(8)

(9)

對于經過ESO反饋之后的式(3)所表示的系統，如果不考慮ESO估計誤差，可近似認為該系統變為一個線性系統，極點配置法求得其反饋增益。用uo來表示經過ESO反饋之后的控制輸入：

u0=-k1e1-k2e2-…-kmem

(10)

其中：ki(i=1，2，…，m)為反饋增益。

綜合式(6)、(7)和(10)可得勵磁控制輸入：

(11)

其中：b0為系統控制輸入u0的系數。

4 設計步驟

1)首先應用目標全息反饋法在單機無窮大系統選取期望的跟蹤值

ei=[Pe-Pe0，ω-ω0，Ut-Ut0]T

(i=1，2，3)

(12)

v=Cv1+Cv2Ef

(13)

其中：

得到需要的Brunovsky標準型，系統中所有的非線性因素歸結到含有機端電壓的狀態方程中。

2)其次構造二階的ESO，w1跟蹤e3，w2跟蹤Cv1+Cv2Ef，通過反饋線性化將未知擾動抵消。

3)應用極點配置法設計經過ESO反饋之后的控制變量u0：

u0=-k1e1-k2e2-k3e3

(14)

5 仿真分析

考慮勵磁限幅作用，上下限值分別為±2。

分別采用以下兩種勵磁控制器：

1)AVR+PSS，勵磁系統AVR用機端電壓偏差值為輸入信號，PSS用轉速偏差為輸入信號；

2)本文設計的勵磁控制器，其中ESO的參數

β01=100，α1=0.25，r=0.001；

β02=300，α1=0.5，r=0.001。

通過ESO反饋線性化和極點配置法可得到勵磁規律為

(15)

5.1 原動機輸入擾動

在1 s時，原動機的輸出功率Pm發生10%的階躍擾動，動態響應曲線如圖1所示，其中實線代表本文提出的勵磁控制器，虛線則對應AVR+PSS。

(a) 功角響應曲線

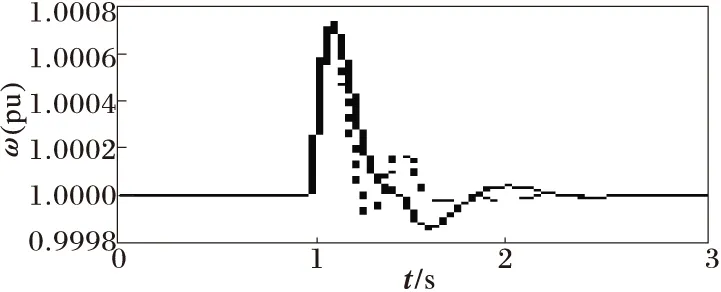
(b) 角速度響應曲線

(c) 電磁功率響應曲線

(d) 機端電壓響應曲線

從圖1可看出在兩種不同勵磁控制器作用下，除了本文功角曲線的幅值略大于AVR+PSS外，其他的三個均小于AVR+PSS。從仿真曲線上看，本文提出的勵磁控制器使得功率振蕩受到一定的抑制，而且減少了機端電壓的高頻波動。因此該勵磁控制器能夠改善系統的小干擾穩定性。

5.2 三相短路擾動

故障2為輸電線路0.1 s時發生瞬時的三相短路，持續時間為0.1 s。發電機有功功率Pe、機端電壓Ut的動態響應曲線分別如圖2所示。

(a) 功角響應曲線

(b) 角速度響應曲線

(c) 電磁功率響應曲線

(d) 機端電壓響應曲線

從上圖可看出在兩種不同勵磁控制器作用下，功率振蕩時間分別為2 s、1 s。并且從仿真曲線上看，本文提出的勵磁控制器使狀態變量有效地抑制了振蕩幅值，減少了調節時間，同時電壓的高頻振蕩也得到明顯的抑制。因此該勵磁控制器也可以改善系統的暫態穩定性。

6 結語

本文將目標全息反饋和ESO應用于勵磁系統的控制器的設計，該法所對應的勵磁規律沒有涉及較多的系統參數，使得控制器的設計變得簡便可行。目標全息反饋可以選取系統較為關心的指標作為系統的狀態變量，實現協調了系統的協調控制。由于ESO具有優良的跟蹤特性,消除了系統中的不確定因素。ESO反饋之后的反饋參數可以使用極點配置法整定，降低了參數選擇的難度。仿真結果證明了上述方法的有效性。

[1] 梅生偉,黎雄，盧強，等(Mei Shengwei,Li Xiong, Lu Qiang,etal).基于反饋線性化方法的勵磁系統非線性H_∞控制研究(Nonlinear H_∞ control for excitation systems via feedback linearization method)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA),1999,11(4):1-7.

[2] 高朝暉,林輝,張曉斌(Gao Zhaohui,Lin Hui,Zhang Xiaobin). Boost變換器帶恒功率負載狀態反饋精確線性化與最優跟蹤控制技術研究(Exact linearization and optimal tracking control of boost converter with constant power loads)[J]．中國電機工程學報(Proceedings of CSEE),2007,27(13):70-75．

[3] 顏偉,吳文勝,華智明,等(Yang Wei,Wu Wensheng,Hua Zhiming,etal).SSSC非線性控制的直接反饋線性化方法(Direct feedback linearization method for designing SSSC nonlinear control law)[J].中國電機工程學報(Proceedings of CSEE),2003,23(3):65-68.

[4] 劉棟良,嚴偉燦,趙光宙(Liu Dongliang,Yan Weican,Zhao Guangzhou).基于轉矩擾動估計的電機反饋線性化控制(Feedback linearization control of motor with torque disturbance estimation) [J].電力系統及其自動化學報(Proceedings of the CSU-EPSA), 2005，17(5)：60-63．

[5] 曹建榮,虞烈,謝友柏(Cao Jiangrong,Yu Lie,Xie Youbai).磁懸浮電動機的狀態反饋線性化控制(Dynamic feedback linearization control for induction-type bearingless motor)[J].中國電機工程學報(Proceedings of the CSEE),2001,21(9):22-26,73.

[6] 劉輝,李嘯驄,韋化(Liu Hui,Li Xiaocong,Wei Hua). 基于目標全息反饋法的單輸入多輸出控制系統極點配置(Pole assignment of nonlinear control with objective holographic feedbacks for the single input multiple output controlled system) [J].中國電機工程學報(Proceedings of the CSEE), 2008,28(4):59-64.

[7] 劉輝，李嘯驄，韋化(Liu Hui,Li Xiaocong, Wei Hua).基于目標全息反饋的發電機非線性綜合控制設計(Nonlinear integrated control design for generator unit based on NCOHF)[J].中國電機工程學報(Proceedings of CSEE),2007, 27(4):21-25.

[8] 劉輝，李嘯驄，韋化(Liu Hui,Li Xiaocong,Wei Hua). 基于目標全息反饋法的發電機非線性勵磁控制器設計(Nonlinear excitation control for generator unit based on NCOHF)[J].中國電機工程學報(Proceedings of CSEE),2007,27(1):14-18.

[9] 邵立偉,廖曉鐘,夏元清,等(Shao Liwei,Liao Xiaozhong,Xia Yuanqing,etal).三階離散擴張狀態觀測器的穩定性分析及其綜合(Stability analysis and synthesis of third order discrete extended state observer)[J].信息與控制(Information and Control),2008,37(2):135-139.

[10]余濤, 朱守真，沈善德, 等(Yu Tao, Zhu Shouzhen, Shen Shande,etal).基于擴張狀態觀測器的電力系統非線性魯棒協調控制(Extended state observer based nonlinear robust coordinated control of power systems)[J].中國電機工程學報(Proceedings of the CSEE), 2004,24(4):1-5.

[11]夏長亮,劉均華,俞衛,等(Xia Changliang,Liu Junhua,Yu Wei,etal).基于擴張狀態觀測器的永磁無刷直流電機滑模變結構控制(Variable structure control of BLDCM based on extended state observer)[J].中國電機工程學報(Proceedings of the CSEE),2006,26(20): 139-143.

[12]康忠健，孟繁玉(Kang Zhongjian,Meng Fanyu).基于擴張狀態觀測器的SVC非線性變結構控制(Nonlinear variable structure SVC control based on extended-states-observer)[J]. 繼電器(Replay)，2007,35(22):10-13.

常家寧(1986-)，男，碩士研究生，研究方向為電力系統及其自動化穩定與控制。Email:yaiba1111@163.com

贠旭明(1970-)，男，工程師，主要從事電力工程、火力發電廠技術。Email:yunxm@163.com

于紫南(1985-)，男，碩士研究生，研究方向為電力系統穩定與控制。Email:yhyuzinan@163.com

GeneratorNon-linearExcitationControllerBasedonObjectiveHolographicFeedbacksandExtendedStateObserver

CHANG Jia-ning1， YUN Xu-ming2， YU Zi-nan3， XIE Guo-qiang4

(1.Chongqing Changshou Power Supply Bureau, Chongqing 401220, China;2.Supplies Department of China Chongxin Hydro Power Generation Co., Ltd,Pingliang 744200, China;3.Jilin Power Supply Co.,LTD., Jilin 132012, China;4.Jiangxi Electric Power Research Institute, Nanchang 330000, China)

In order to obtain the corresponding Brunovsky standard type, nonlinear factors of the nonlinear affine system' equation was switched to the state equation which contains the control input factors through the targeted holographic feedback. After the switch, the nonlinear factors of system will be comprised in the suppositional control input equation. Construct a second order ESO to observe the unknown part of system and linearize the feedback, then the linear model will be obtained. The next step is to obtain the feedback gain coefficient of the system's linear part through the method of pole assignment. Finally, MATLAB was used for simulating and the result show the effectiveness of the method.

excitation control； objective holographic feedbacks； extended state observer(ESO)； pole allocation； Brunovsky standard

TM571

A

1003-8930(2012)06-0143-05

2011-05-31；

2011-08-26