基于SSI-TLS法的同步電機參數辨識

潘學萍， 陶正華

(河海大學能源與電氣學院， 南京 211100)

基于SSI-TLS法的同步電機參數辨識

潘學萍， 陶正華

(河海大學能源與電氣學院， 南京 211100)

提出基于隨機子空間和總體最小二乘相結合的同步電機參數識別新方法。根據同步電機三相短路后a相電流的時間序列，由隨機子空間法辨識出電流各分量的頻率和衰減因子；再由總體最小二乘法求得各分量的幅值，據此辨識得同步電機各參數。仿真算例表明了文中提出的方法可用于同步電機的參數辨識，并通過與現有方法的對比表明該法可提高參數辨識的精度。

同步發電機； 隨機子空間法； 總體最小二乘； 參數辨識

合理而精確的同步電機參數對電力系統電磁暫態和機電暫態的仿真分析的正確性尤為重要，如何得到更接近實際的同步電機參數成了眾多學者研究的熱點。同步電機參數的獲取主要有數值分析法、實驗測試法、頻域響應法和時域響應法，合適的參數辨識方法對同步電機參數的獲取至關重要。

同步電機瞬態參數[1]的求解一般根據發電機出口短路電流的包絡線，得到短路電流的周期分量和非周期分量，但是該方法精度不高，有較大的誤差[2]。文獻[3]應用Prony方法辨識同步電機的參數，該方法對噪聲敏感，辨識結果誤差較大[4]。文獻[5]應用希爾伯特-黃變換方法辨識同步電機參數分析精度較高，但其經驗模態分解存在端點效應問題[6]。文獻[7]提出了基于小波變換的處理方法，有很高的精度，但小波方法在實際應用中存在小波基選取問題[5]。文獻[4]基于總體最小二乘法和旋轉不變技術法TLS-ESPRIT(total least squares-estimation of signal parameters via rotational invariance technigue)，該方法抗噪能力強，辨識精度高，但是需要進行兩次奇異值分解，使得計算量增大[8]。文獻[6]提出了基于隨機子空間的同步電機參數辨識方法，但對于有阻尼的系統，所辨識的幅值誤差較大。本文在該方法的基礎上，提出將隨機子空間和總體最小二乘相結合的同步電機參數識別方法，提高有阻尼系統的幅值辨識精度。文獻[8]將該方法用于提取電力系統低頻振蕩模式信息，辨識精度較高。

文中首先基于SSI算法，從三相短路電流中提取各頻率分量及其衰減因子；再采用TLS方法，對采樣數據進行二次消除噪聲處理，獲得陣型信息，并計算各分量幅值，進而得出同步發電機各參數。最后通過仿真算例進行了驗證。

1 SSI-TLS方法

1.1SSI方法

線性系統狀態方程為

(1)

式中：Yk為測量數據向量；Xk∈Rn×1，Xk為狀態向量；Wk為過程噪聲；Vk為測量噪聲；n是系統的階數；A、C分別是系統狀態和輸出矩陣。由輸出數據Yk組成一個塊Hankel矩陣，使其分成過去Yp和將來Yf兩部分：

(2)

Yf的行空間在Yp上形成的正交投影為：

(3)

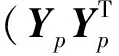
(4)

對投影矩陣進行奇異值分解得：

(5)

由式(4)、(5)得：

(6)

(7)

由式(1)得系統狀態矩陣：

(8)

1.2 特征頻率與衰減因子

對狀態矩陣A進行特征值分解：

A=ΨΛΨ-1

(9)

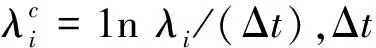
(10)

(11)

1.3 總體最小二乘法求幅值

由總體最小二乘法求出各個特征頻率對應的電流分量的幅值為

Y=Λc

(12)

式中，Y=[y1y2…yN]T；

c=[c1c2…cn]T

由式(12)得：

c=(ΛHΛ)-1ΛHY

(13)

各分量的幅值Ai為

Ai=2|ci|，i=1，2，…，n

(14)

其中特征頻率、衰減因子和幅值一一對應。

2 合成信號的參數辨識

以式(15)的合成信號為例，分析不同噪聲強度下SSI-TLS法的辨識精度。

y=e-14tcos(100πt)+0.2e-2t·

cos(200πt)+0.1e-1+e(t)

(15)

該信號包含1衰減分量及2個振蕩衰減分量，e(t)為白噪聲。設信噪比為50 dB，采樣頻率為1 kHz，采樣窗口為2 s。該信號的波形見圖1。

由公式(1)可知，隨機子空間法參數辨識時需預先確定系統的階數。對于階數不能預先確定的系統，可根據穩定圖法、或者通過陣型圖和奇異值跳轉[6]等方法先確定系統的階數。本例中，系統有三個模式，因此在疊加噪聲后可設定系統階次為5階。基于SSI-TLS法辨識得到各模式頻率與幅值，見表1。表1中同時給出了單獨采用SSI方法的辨識結果。

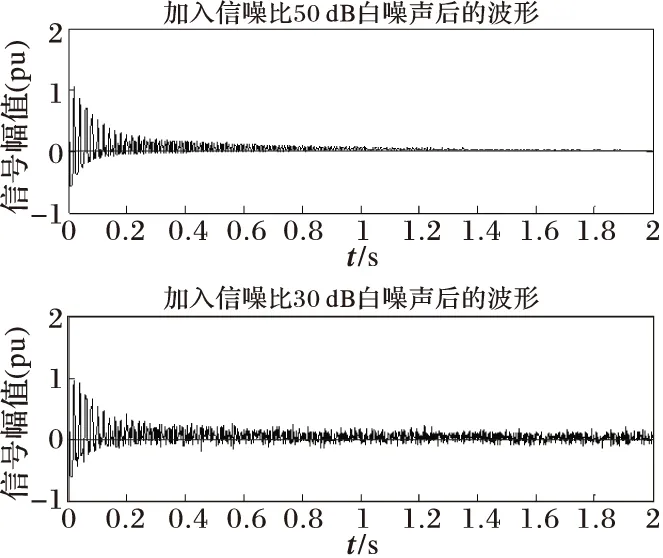
圖1 合成信號

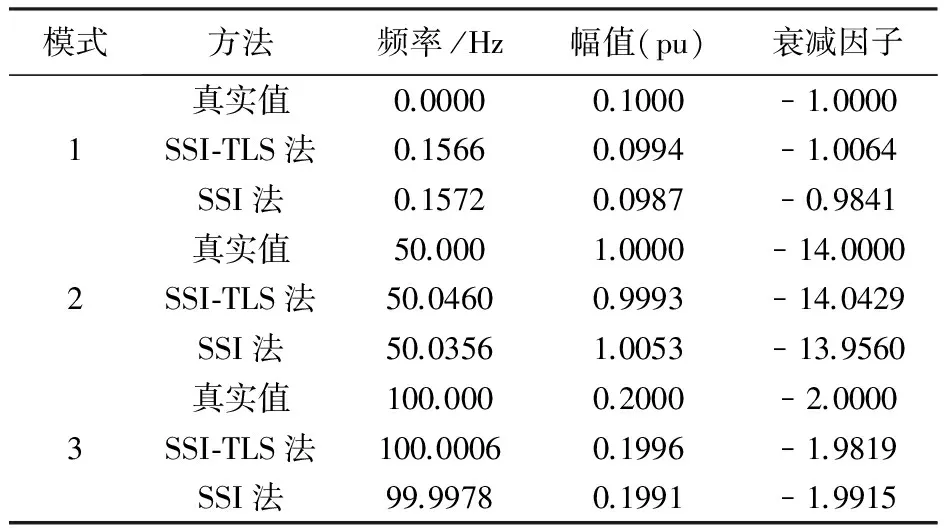
表1 SSI-TLS法和SSI法估計結果和真實值比較

從辨識結果來看，SSI-TLS法幅值計算結果較SSI法精確。同時本文的方法因不需要多次代入消去指數衰減，可以直接辨識得到各分量頻率、幅值和衰減因子，因而速度較快。增大信號內的噪聲含量，將信噪比由原來的50 dB增加到30 dB，采樣頻率同上，信號波形如圖1。基于SSI-TLS法和SSI法對系統模式進行辨識，辨識結果見表2。

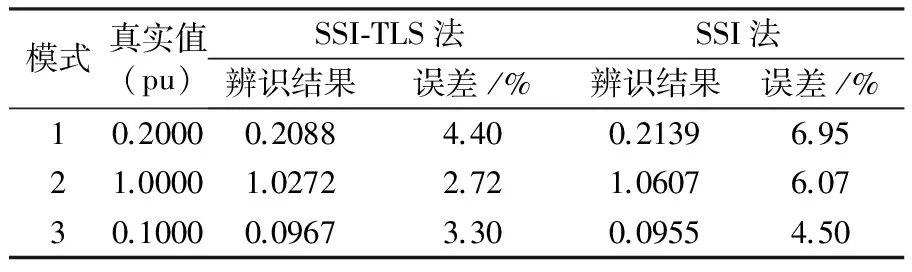
表2 兩種方法的幅值辨識結果

由表2可以看出，信號內的噪聲強度增大時，SSI-TLS辨識精度大于SSI法。這主要是因為SSI方法引入TLS后，實現了對信號的二次消噪處理，增強了抗噪能力。

3 基于SSI-TLS的同步電機參數辨識方法

進一步以同步發電機短路電流作為量測信號，辨識同步發電機各參數。設該電機的各參數(以發電機容量為基準的標幺值)為

發電機端口突然發生3相短路時，初相角φ0=π/3，內電動勢E=1，基波頻率為f=50 Hz。電機發生突然三相短路后的a相電流波形見圖2。設信噪比為45 dB，采樣頻率為1 kHz，采樣窗口為2 s。

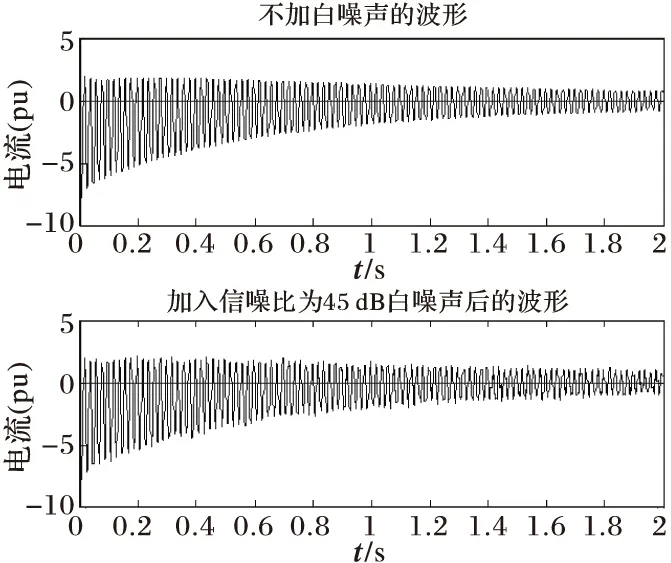
圖2 同步電機短路電流波形

由理論分析可知，同步發電機三相短路后a相電流[9]表達式如下：

(16)

式中前3部分分別為直流分量、二次諧波分量和基波分量，e(t)為噪聲。

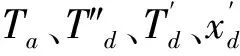
表3給出了有噪聲和無噪聲兩種情況下的辨識結果，以及SSI方法辨識結果。

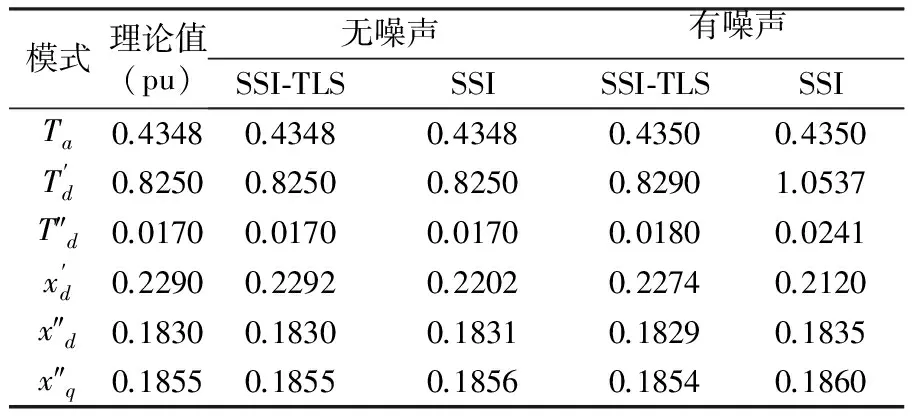
表3 兩種方法的辨識結果

由表3可知，與SSI法相比，SSI-TLS法提高了瞬態和超瞬態參數的辨識精度。在有噪聲的情況下，本文方法抗噪能力較強，瞬態參數和超瞬態參數的辨識精度較高。

圖3是辨識所得波形與實際波形的比較(為便于觀察，僅取采樣時間1.8～2 s)，由圖3可知，兩者高度吻合。

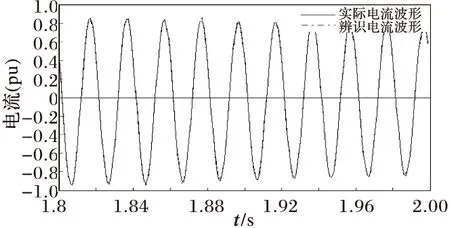
圖3 實際波形和辨識所得波形比較

4 結語

針對SSI方法對噪聲敏感、對有阻尼的模式幅值辨識誤差較大的問題，本文提出采用SSI與TLS相結合的方法進行同步發電機的參數辨識。通過人工合成算例以及同步發電機故障后的電流波形的參數辨識結果表明， TLS的引入，可增強SSI方法的抗噪聲能力，且克服SSI法無法準確辨識有阻尼系統的幅值的缺點，因而可提高參數的辨識精度。同時SSI和TLS結合后，使得辨識步驟更加簡單，可實現同步電機參數的一步辨識。通過仿真算例驗證了本文方法的有效性和優越性。

[1] 馬宏忠，胡虔生，方瑞明(Ma Hongzhong,Hu Qiansheng, Fang Reiming). 同步電機瞬變參數的測量(Transient parameter measurement of synchronous machine)[J].電力系統及其自動化學報(Proceeding of CSU-EPSA)，2000，12(2)： 8-12.

[2] 吳旭升，馬偉明，王公寶，等(Wu Xusheng，Ma Weiming，Wang Gongbao，etal).基于小波變換和Prony算法的同步電機參數辨識(Parameter identification of synchronous machine based on wavelet transform and Prony algorithm)[J]．電力系統自動化(Automation of Electric Power Systems)，2003，27(19)：38-42．

[3] 蘇小林，周雙喜( Su Xiaolin，Zhou Shuangxi ).Prony法在同步發電機參數辨識中應用(Application of Prony method to parameter identification of synchronous generators)[J].電力自動化設備(Electric Power Automation Equipment)，2006，26(9)：1-4.

[4] 李天云，祝磊，宋莉，等( Li Tianyun，Zhu Lei，Song Li，etal).基于TLS-ESPRIT的同步電機參數辨識(Parameter identification of synchronous machine based on TLS-ESPRIT )[J]. 電工技術學報(Transactions of China Electrotechnical Society)，2009，24(12)：38-42,49.

[5] 李天云，高磊，陳曉東，等(Li Tianyun，Gao Lei，Chen Xiaodong，etal).基于 HHT 的同步電機參數辨識(Parameter identification of synchronous machine based on Hilbert-Huang transform)[J].中國電機工程學報(Proceedings of the CSEE)，2006，26(8)：153-158.

[6] 李玲，李天云，黃紹平，等(Li Ling，Li Tianyun，Huang Shaoping，etal).基于隨機子空間的同步電機參數高精度辨識新方法(A high-precision approach to identify synchronous generator parameters based on stochastic subspace identification)[J].電網 技 術(Power System Technology)，2011，35(7)：156-160.

[7] 王亮，王公寶，馬偉明，等(Wang Liang，Wang Gongbao，Ma Weiming，etal).基于小波變換和神經網絡的同步電機參數辨識新方法(A new method for parameters identification of synchronous electric machine based on wavelet transform and neural network)[J]．中國電機工程學報(Proceedings of the CSEE)，2007，27(3)：1-6.

[8] 袁榮湘，江保鋒，趙樹華，等( Yuan Rongxiang，Jiang Baofeng，Zhao Shuhua，etal).隨機子空間法在低頻振蕩分析中的應用(Stochastic subspace identification for power system low frequency oscillations analysis)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA)，2011， 23(4)：51-55.

[9] 高景德，王祥珩，李發海.交流電機及其系統的分析[M].北京：清華大學出版社，1993.

[10]蔡國偉，楊德友，張俊豐，等(Cai Guowei，Yang Deyou，Zhang Junfeng，etal).基于實測信號的電力系統低頻振蕩模態辨識(Mode identification of power system low-frequency oscillation based on measured signal)[J].電網技術(Power System Technology)，2011， 35(1)：59-65.

[11]李天云，袁明哲，許廣婷，等(Li Tianyun ，Yuan Mingzhe ，Xu Guangting，etal).基于隨機子空間結合穩定圖的間諧波高精度檢測方法(An inter-harmonics high-accuracy detection method based on stochastic subspace and stabilization diagram)[J].電力系統自動化(Automation of Electric Power Systems)，2010，34(20)：50-54.

[12]張少康，李興源，王渝紅，等(Zhang Shaokang，Li Xingyuan，Wang Yuhong，etal). Prony算法在汽輪機調節系統參數辨識中的應用(Prony algorithm applied to steam turbine governing system parameter identification)[J].電力系統及其自動化學報(Proceeding of CSU-EPSA)，2010，22(6)：23-27.

[13]王興貴，王言徐，智勇(Wang Xinggui， Wang Yanxu， Zhi Yong). 遺傳算法在發電機勵磁系統參數辨識中的應用(Application of genetic algorithm in generator excitation system parameters identification)[J].電力系統及其自動化學報(Proceeding of CSU-EPSA)，2010，22(1)：76-79.

[14]劉取.電力系統穩定性及發電機勵磁控制[M]. 北京：中國電力出版社，2007.

潘學萍(1972-)，女，博士，副教授，研究方向為電力系統分析與控制。Email:xueping_pan@163.com

陶正華(1987-)，男，碩士研究生，研究方向為風電機組參數辨識。Email:taozhenghua910@163.com

ParameterEstimationofSynchronousMachineBasedonSSI-TLS

PAN Xue-ping， TAO Zheng-hua

(College of Energy and Electrical Engineering，Hohai University，Nanjing 211100，China)

A new method is proposed in this paper for synchronous parameter estimation. This method includes two stage estimation processes. The first stage uses stochastic subspace identification (SSI) method to estimate frequency and damping ratio of each current component based on measuring a-phase post-fault current. And then the next stage considers total least squares (TLS) in order to estimate the magnitude of each oscillatory component based on the parameters of synchronous machine. Simulations show that the method proposed in this paper can improve the estimation accuracy.

synchronous machine； stochastic subspace identification(SSI)； total least squares(TLS)； parameter identification

TM301

A

1003-8930(2012)06-0058-04

2012-07-13；

2012-08-16