ANSYS在傳熱學多媒體教學中的應用

劉輝敏

洛陽理工學院 河南洛陽 471023

ANSYS在傳熱學多媒體教學中的應用

劉輝敏

洛陽理工學院 河南洛陽 471023

為改善教學效果，將ANSYS引入傳熱學多媒體課程。介紹了傳熱計算相關理論，以典型的傳熱過程為例，采用ANSYS對其溫度場進行了分析。采用ANSYS能夠調動課堂氣氛，有利于學生對知識點的掌握。

ANSYS；傳熱學；多媒體教學；有限單元法

材料工程基礎是高等學校無機非金屬材料工程專業的一門重要專業基礎課程，傳熱學則是本課程的重點和難點之一。傳熱學的主要特點為抽象概念多，理論性強，數學基礎要求高。對于這門課程，學生首先應理解基本概念，掌握理論知識，然后能夠將其應用于分析解決實際問題。然而，學生在對傳熱學問題進行計算時，只有簡單問題才能求出理論解，對于許多復雜問題則顯得無能為力，以致影響其對本課程的掌握和學習興趣。將ANSYS數值模擬引入傳熱學多媒體教學，可對復雜結構及現象進行可視化分析，而且重要物理量的變化過程可通過圖像顯示出來，從而激發學生學習興趣。

1 溫度場的計算

1.1 導熱方程

在固體介質中，熱傳導服從傅立葉定律。對于一般三維傳熱問題，瞬態溫度場的場變量T(x，y，z，t)在直角坐標系中滿足如下方程：

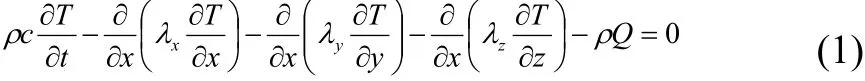
式中，T－材料的瞬態溫度，℃；t—經歷的時間，s；λx，λy，λz—材料沿x，y，z方向的導熱系數，W/m?℃；ρ—材料密度，kg/m3；c—材料比熱，kJ/kg?℃；Q—物體內部熱源密度，W/kg。

式(1)中，第一項是體元升溫需要的熱量；第二、三和四項是由x，y和z方向流入體元的熱量；最后一項是體元內熱源產生的熱量。上述方程，必須附加初始條件和邊界條件才能得到唯一解。

1.2 初始條件與邊界條件

1.2.1 初始條件

指所求解問題的初始溫度場，也就是在零時刻的溫度分布，可用式(2)來表示：

式中，T0(x，y，z)為已知溫度函數。

一是防汛抗旱減災成效顯著。堅持防汛抗旱兩手抓，冬春共投入抗旱資金16.7億元，抗旱澆灌面積5 878萬畝（391.87萬hm2），為全省糧食生產實現“十連增”提供了有力保障；科學處置7次較強降雨過程，汛期全省共緊急轉移群眾11 381人。組織開展了近年來規模最大的清障行動，投入資金1億元，出動人員10萬人次，動用機械1萬余臺次，完成清除樹障、阻水違章建筑等清理任務985項，特別是清理了多年未能解決的灤河入海口養殖蝦池約6 000畝（400 hm2），確保了全省防洪安全。

1.2.2 邊界條件

指物體表面或邊界與周圍環境的熱交換情況，通常有三類重要的邊界條件。

(1)第一類邊界條件。指物體邊界上的溫度分布函數已知，用公式表示為：

式中，Tw(x，y，z，t)為已知的物體表面的溫度分布函數，隨時間和位置的變化而變化。

(2)第二類邊界條件。指物體邊界上的熱流密度已知，用公式表示為：

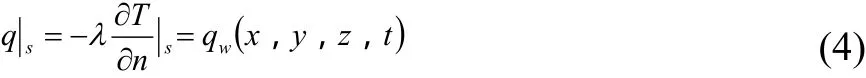
式中，qw(x，y，z，t)為已知的物體表面的熱流密度分布函數，隨時間和位置的變化而變化。

(3)第三類邊界條件。指物體與其周圍環境介質間的對流傳熱系數和介質的溫度已知，用公式表示為：

式中，k—對流傳熱系數；Tf—介質溫度。k和Tf可以是已知的常數，也可以是某種已知的分布函數。

實際生產中的許多傳熱問題，雖然也可用數學分析法解出，但運算過程十分煩瑣，倘若問題的幾何條件和邊界條件比較復雜，用數學分析法就更加困難，有時甚至不能求解。此時，采用有限單元法將是最佳的選擇。

1.3 有限單元法

有限單元法被廣泛應用于傳熱問題計算中，它特別適用于數值求解非線性熱傳導問題以及具有不規則幾何形狀和邊界的復雜導熱問題。有限單元法的基本思想可歸納如下：

(1)將結構連續體離散為若干個單元，各單元通過其邊界上的結點連接成組合體。(2)用近似函數分片地表示全求解域內待求的未知變量，而單元內的近似函數用未知場變量在單元各結點上的數值與其對應的插值函數表示，從而將求解原函數無窮多自由度問題轉換為求解場變量函數結點值的有限自由度問題。(3)通過和原問題數學模型等效的變分原理或加權余量法，建立求解場變量函數結點值的代數方程或常微分方程，并應用數學方法求解得到答案。

概言之，有限元分析問題的主要步驟為問題及求解域定義，求解域離散化，確定狀態變量及控制方法，單元推導，總裝求解，聯立方程組求解和結果解釋。

2 ANSYS在傳熱學教學中的應用

ANSYS是一種通用有限元軟件，它在溫度場分析中得到十分廣泛的應用。在結構上，該軟件具有前處理、分析器及后處理三個基本模塊。利用這三個模塊，就可以解決傳熱學課程教學中遇到的問題。前處理器的主要功能包括單元選用、定義單元特性及材料性質、產生有限元模型。分析器是最重要的部分，通過它主要確定分析方式及其解法選項、設定約束邊界條件、設置外力或能量源的邊界條件、設置輸入/輸出控制或求解。后處理器則主要是將計算結果以圖形或文字形式輸出。ANSYS分析處理作業流程如下：

前置設置→進入前處理器→選用適當的單元，定義單元特性及材料性質→建立被分析物體的實體模型→產生有限元模型→離開前處理器→進入分析器→確定分析方式及其解法選項→設置約束邊界條件→設置外力或能量源的邊界條件→設置輸出控制與求解→離開分析器→進入后處理器→輸出圖形或文字信息→離開后處理器。

在課程教學中，可先將書本上的基本概念、基本原理采用傳統教學方法講授，力求使學生理解與掌握。在此基礎上，利用ANSYS解決一些典型的、復雜的傳熱問題，并演示在傳統教學中不能得到的一些重要物理量的變化過程及其他重要信息，使學生加深對概念和基本原理的理解。

對于傳熱學問題，應用ANSYS可實現對傳導傳熱、對流傳熱、輻射傳熱以及相變問題等進行靜態和動態分析，以下舉例分別加以說明。

3 示例

3.1 鋼球冷卻過程分析

有一個半徑為150mm，初始溫度為1 000℃的銅球，將其突然置于溫度為30℃且對流換熱系數為60W/(m2?℃)的流體介質中。計算：(1)第10s時整個銅球的溫度分布；(2)銅球表面任一點的溫度在50s內的變化情況。已知銅球的比熱容為390J/kg?℃，密度為8 900kg/m3，熱導率為383W/(m?℃)。

本例可簡化為二維平面分析問題，選用PLANE55平面單元進行瞬態分析，結果分別如圖1和圖2所示。

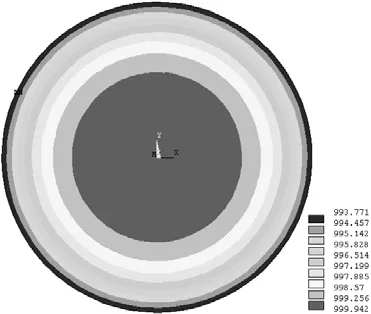
圖1 第15 s時銅球的溫度分布

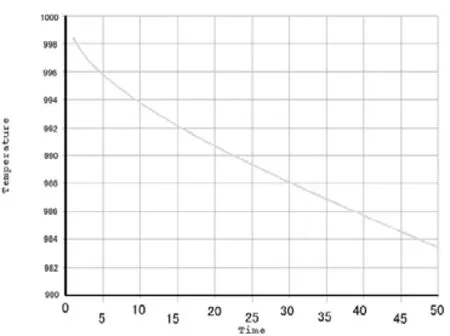
圖2 銅球表面任一點溫度在50 s內的變化情況

3.2 兩圓柱間熱輻射分析

有兩個圓柱C1和C2，它們之間的位置關系如圖3所示。C1的外徑為1.0in，內徑為0.75in；C2的外徑為0.5in，內徑為0.25in，兩圓柱中心相距0.2in。C1外表面溫度為120℃，內表面輻射系數為0.6。C2內表面溫度為1 200℃，外表面輻射系數為0.9。環境溫度恒為80℃，計算兩圓柱之間的溫度分布情況。

假設兩圓柱無限長，忽略長度方向的影響，故本例可簡化為二維平面問題，選用PLANE35六節點二階三角形平面單元進行靜態分析，結果如圖4所示。

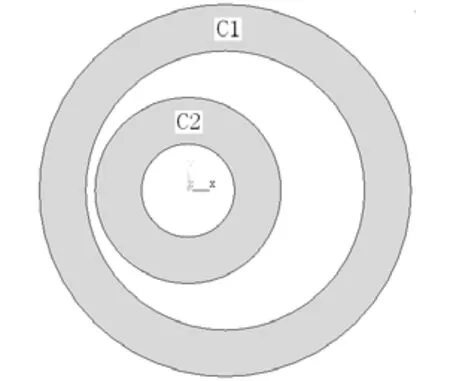
圖3 幾何模型圖

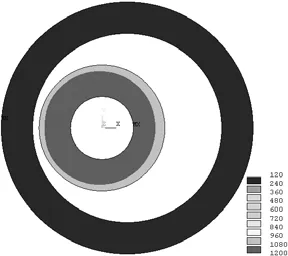
圖4 兩圓柱之間的溫度分布

3.3 茶杯中水結冰過程分析

一圓柱形玻璃杯，直徑為60mm，高度為90mm。杯內盛有初始溫度為0℃的水，環境溫度為-25℃，試對杯中水的結冰過程進行分析。已知杯中水的頂面及側面的對流傳熱系數均為20 W/(m2?℃)，水的材料參數見表1。計算45min內玻璃杯中水的溫度場分布情況，以及玻璃杯邊緣點A處的溫度和熱流密度變化情況(點A位于圓柱母線的中點)。

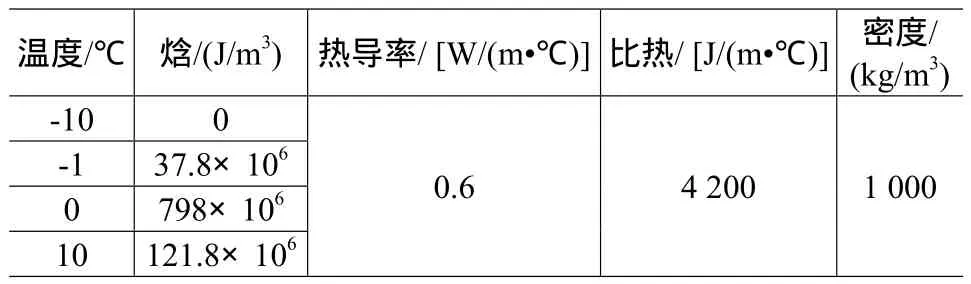
表1 水的材料參數

本例屬于軸對稱問題，采用二維4節點平面熱分析PLANE55單元進行有限元分析。在第15min、第30min和第45min時，玻璃杯中水的溫度場分布分別見圖5所示。點A處溫度和熱流密度隨時間的變化情況分別見圖6和圖7所示。

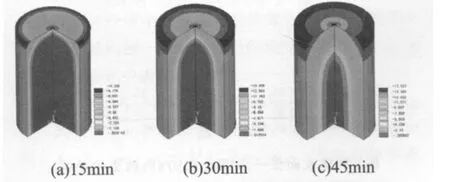
圖5 玻璃杯中水的溫度場分布

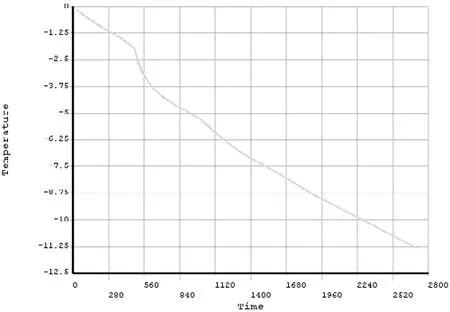
圖6 點A處溫度隨時間的變化

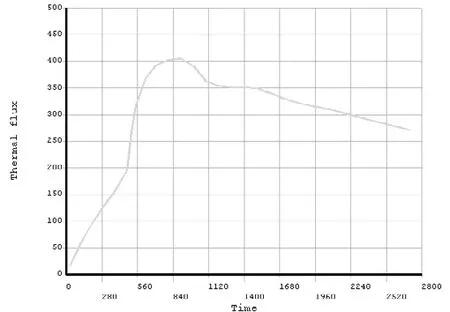
圖7 點A處熱流密度隨時間的變化

通過以上分析可知，ANSYS可提供豐富而重要的信息，使學生對物體傳熱過程中的等溫線、熱流量、路徑上的溫度分布以及溫度場的變化情況有更為全面和直觀的了解，幫助學生對基本概念和理論知識的理解、消化與記憶。實踐表明，在枯燥的理論講解及公式推導過程中配以ANSYS數值模擬，可以調動課堂氣氛，增加學生的學習興趣，提高教學效果。

ANSYS在解決復雜傳熱問題時具有直觀、生動、快速和信息豐富的特點，將其應用于傳熱學多媒體教學，能夠調動課堂氣氛，激發學生學習興趣，有利于他們對知識點的掌握。

[1] 徐德龍,謝俊林.材料工程基礎[M].武漢:武漢理工大學出版社,2008.

[2] 劉建軍.基于ANSYS的硅酸鹽熱工基礎課程教學模式探討[J].中國陶瓷,2006,4(21):47-50.

[3] 許鑫華.計算機在材料科學中的應用[M].北京:機械工業出版社,2003.

[4] 周昌玉,賀小華.有限元分析的基本方法及工程應用[M].北京:化學工業出版社,2006.

[5] 張國志,胡仁喜,陳繼剛.ANSYS10.0熱力學有限元分析實例指導教程[M].北京:機械工業出版社,2003.

Application of ANSYS in heat transfer multimedia teaching

Liu Huimin
Luoyang institute of science and technology, Luoyang, 471023, China

To improve teaching effect, ANSYS was introduced in the heat transfer multimedia course. The correlation theory about heat transfer calculation was introduced, then the temperature field of typical heat transfer process as examples was analyzed by ANSYS. Applying ANSYS to heat transfer multimedia teaching can activate classroom atmosphere, increase students’ learning interesting, and help them mastering knowledge point.

ANSYS; heat transfer; multimedia teaching; f nite element method

2011-10-07

劉輝敏，博士，副教授。