深部巷道圍巖變形破壞機制分析

李 杰，宋春明，胡 嘯，陳文濤，范鵬賢

(1.解放軍理工大學 爆炸沖擊防震防災國家重點實驗室，南京 210007；2.空軍工程環境質量站，北京 102208)

1 引 言

隨著工程的埋深增加和規模加大，目前在深地下工程的設計和施工過程中遇到了一些共同的難題[1－5]，例如，采用何種支護方法提高圍巖穩定性，如何避免能量突然釋放引起的巖爆等等，要回答這些問題，必須對高地應力條件下深部巖體的變形破壞特性與破壞準則進行詳細的探討。

20世紀80年代初，國外就已經開始針對深部礦井問題進行專題研究。由于巖石工程不斷向深地下發展，一些國家和地區，尤其有深井礦山的國家，美國、俄羅斯、加拿大、澳大利亞、南非，波蘭等都集中人力物力，針對深部開采等相關技術以及基礎問題等展開了深入的研究，取得了巨大的進展[6－7]。

對于深部問題的研究我國雖然起步較晚，但在錢七虎院士等的大力倡導下[8]，我國學者也對深部巖體力學等進行了富有成效的研究，一些科學家對深部巖體的特征科學現象（分區破裂化、沖擊地壓、超低摩擦、巖體的低頻準共振現象等）提出了一系列獨到的觀點，在巖體的結構層次及其形成機制、力學性質的關系、深部巖體的變形與運動特性方面取得了階段性的成果[9－11]，如周小平等[12－13]利用彈性力學理論，得到了在原巖應力及開挖擾動作用下巷道圍巖的彈性應力場及位移場，認為當彈性應力場滿足破裂條件時巖體發生破裂，形成破碎區。戚承志等[14]利用連續相變理論，研究了巷道圍巖的分區破裂化現象。馮夏庭等[15]在錦屏II級水電站工程實踐的基礎上，根據支護要求和控制因素將深埋硬巖隧洞的破壞現象詳細分類，分析各種破壞模式（重點討論巖爆）的發生機制、表現形態以及調控策略等等。

本文在已有研究的基礎上，采用彈脆性本構模型對深部圍巖應力分布以及變形破壞機理進行分析，對深部圍巖支護以及分區破裂化現象機理闡述等都具有一定的意義。

2 數學計算模型

為便于分析，探討圓截面水平坑道的開挖問題，如圖1所示，將問題看作平面應變問題，在極坐標（r,θ）下平衡微分方程及幾何方程分別為[16]：

式中：σr、σθ分別為徑向和環向應力；εr、εθ為徑向和環向應變；ur為徑向位移；γrθ為剪切應變。

坑道掘進時，巷道周圍巖體中發生應力重新分布，其初始狀態為靜水壓力(取柱坐標)：式中：γ0為重度；H為巷道埋深；σr、σθ、σz的上標0表示初始應力。

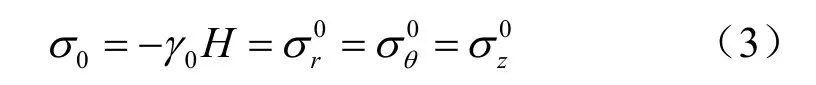
平面應變條件下坑道附近的應力分布通常如圖1所示。圖中， ri為開挖半徑；rc為不可恢復區半徑；pi為支撐壓力；σθmax為峰值支撐壓力，這能在大量實驗中得到，用彈塑性介質或具有摩擦力的介質模型計算能得到同樣的應力分布圖。

在有支承壓力 σθmax的區段附近，最可能的是

2.1 塑性區域的解

考慮到支承壓力 σθmax的增加是的幾倍，以及由于坑道附近不可逆變形的發展，在 ri≤r＜rc的區域產生不可恢復變形區域。為分析簡單，采用如圖2所示的脆性簡化模型。圖中，τ為剪切應力；γ為剪切應變；τf、τs分別為極限剪切強度與殘余強度；γ*為極限剪切應變；μ為剪切模量，這對于闡述機理來說是有好處的，因為復雜的模型往往會掩蓋事物的本質。

圖2 脆性簡化模型Fig.2 Brittle failure model

巖體強度準則采用Tresca準則：

如達到極限剪切應變，應力降為殘余強度：

從滑移破壞的觀點來看，數值τf是由連續介質變形到“破壞”的過渡點，這時 γ=γ*，滑移面上剪切的發展確定了材料的峰值后的性狀，當 γ≥γ*時，巖體被滑移線網格分劃成具有一定尺度的塊體（或條帶），它們之間的相互摩擦決定著殘余強度的大小。

2.2 彈性區域的解

在彈性區域，r≥rc，由胡克定律有力-應變關系為

式中：λ、μ為拉梅系數。

將式（8）代入平衡微分方程式（1）可得

式（9）的解的一般形式可以寫成

結合邊界條件以及連續性條件：

計算可得彈性區內的應力以及位移：

對于不可恢復區的位移可以按不同的假設計算，設不可恢復區的體積變化是彈性的，則

方程式（15）的解為

2.3 算例

令 σc=2τs，計算可以得到

（1）不可恢復區半徑

由式（14）可以計算出不可恢復區半徑，對其進行無量綱化處理，可以得到如下公式：

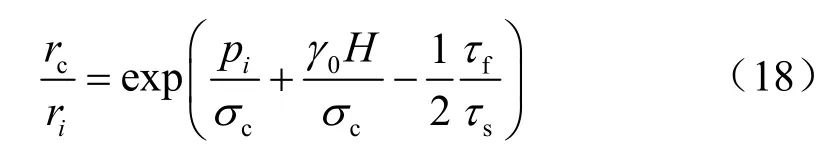
如果不考慮支護強度的影響，要使深地下開挖周圍圍巖產生不可恢復區的條件為

圖 3、4分別為不同支護強度和開挖深度對不可恢復區半徑的影響曲線(計算取τf/τs=3/2)，同時由參考公式(4.23)可以知道，支護條件對不可恢復區的半徑有著深刻的影響，理論上如果對開挖區及時的施加足夠大的支護強度，可以消除不可恢復區的產生，這一臨界條件為

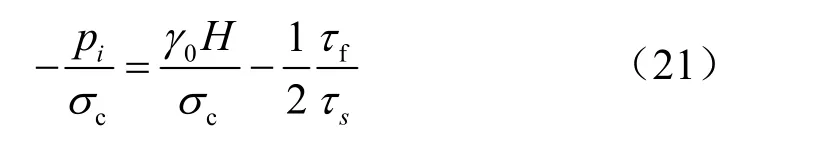
圖3 開挖深度對不可恢復半徑的影響Fig.3 Effects of excavation depth on radius of irrecoverable deformation area

圖4 支護強度對不可恢復半徑的影響Fig.4 Effects of support strength on radius of Irrecoverable deformation area

（2）應力位移分布曲線

利用式（7）、（12）、（13）、（16）可以計算得到周圍圍巖的應力和位移分布曲線。取下列參數進行計算： ri= 3 m，彈性模量 E=5 GPa，泊松比ν=0.25，τs= 15 MPa，τf= 20 MPa，σ0= -45 MPa，pi分別取 pi=0、0.1σ0，可以得到不同支護強度下的應力位移分布曲線，如圖5、6所示。

圖5 不同支護強度下應力分布曲線Fig.5 Stress distribution curves under different support strengths

圖6 不同支護強度下位移分布曲線Fig.6 Displacement distribution curves under different support strengths

取同樣的計算參數，不考慮支護即 pi=0，σ0分別取-σ0=σc=30 MPa，-σ0=1.5σc，-σ0=2σc，則可得不同初始應力狀態下的應力位移分布曲線，如圖7、8所示。

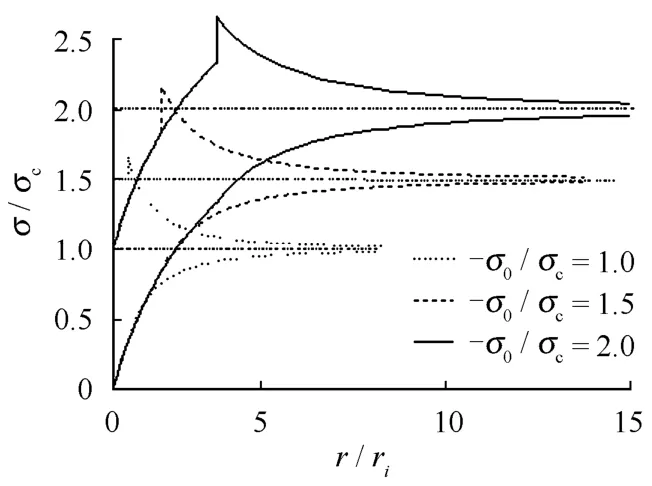
圖7 不同初始應力狀態下應力分布曲線Fig.7 Displacement curves under different initial geostress states

圖8 不同初始應力狀態下位移分布曲線Fig.8 Displacement distribution curves under different initial geostress states

由圖8可見，支護強度對不可恢復區峰值應力值影響不是很大，但是，對于開挖面位移和不可恢復區半徑發展影響很大，當支護強度達到一定程度時，對這種影響逐漸減小，實際工程中應該選擇合適的支護強度以達到施工成本和支護效果的最大優化比。

（3）開挖面位移

在式（16）中，令r=ir可以得到開挖斷面的累計位移，這一位移用ui來表示，則

由式（22）可以繪制徑向位移與初始應力0σ或者支護壓力pi之間的關系曲線，同樣利用參數E =5 GPa，ν=0.25，sτ= 15 MPa，fτ= 20 MPa進行計算，可以得到初始地應力以及支護強度對開挖面誘發位移的影響曲線，分別如圖9、10所示。

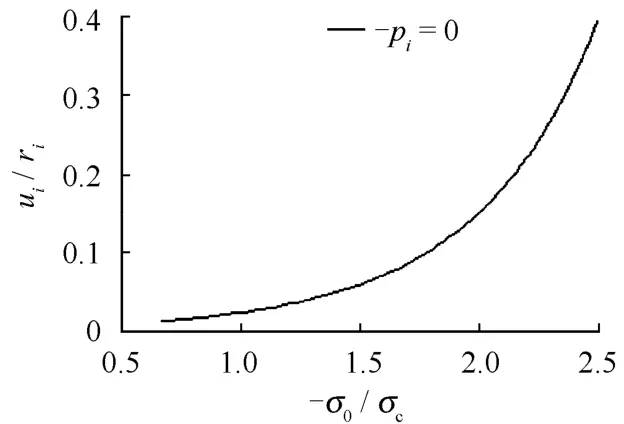
圖9 初始地應力對開挖斷面累計位移的影響Fig.9 The effects of initial geostress on total displacement

圖10 支護強度對開挖斷面累計位移的影響Fig.10 The effect of support strength on total displacement

式（22）以及圖 10對于實際工程的意義也是顯而易見的。利用式（22）可以簡單估算控制洞壁位移時所需的支護壓力，例如，側壁的支護壓力值為通過式（22）計算所得的-pi，頂板以及底板所需的支護壓力值則分別為-pi+γ0（rc-ri）以及-pi-γ0（rc-ri）。

如果在圍巖開挖斷面監測到的位移超出了按式（22）計算的數值，按可認為在最大應力區附近產生了分層剝離(區域拉伸破碎)。

3 區域拉伸破碎條件計算

根據文獻[17]，分層剝離是開挖卸荷圍巖體積變化的主要原因，這也可以用來定性解釋分區破裂化現象，分層剝離使得圍巖開挖斷面監測到的位移大大超出按式（22）計算的數值。

取峰值壓力(r=rc)附近區域的巖體單元進行研究，由上述計算可知，開挖卸荷的過程中，所取單元的應力狀態由最初的靜水壓力狀態逐步轉變成與峰值應力相對應的應力狀態（圖 11中(a)狀態轉變為(b)狀態），如果進一步開挖卸荷，剪切應力τrθ=（σr-σθ）/2將達到極限狀態從而進入反向屈服階段，產生塑性流動。

圖11 巖體單元應力狀態演化示意圖Fig.11 Stress state evolution sketch of the rock mass unit

這樣所研究單元在大的軸向應力σθ以及小 的徑向應力σr壓縮作用下，其徑向位移εr很容易 達到極限拉伸應變，從而產生“分層剝離”，下面計算產生區域拉伸破碎的條件，為方便計算，引入下列張量符號[18]：

式中：σij為應力張量；δij為特克羅內克爾記號；p為靜水力；Sij為偏應力張量。則建議的本構模型可以用下式表示：

式中：εij為應變張量；為塑性應變張量；Kp為考慮到體積膨脹的體積模量。

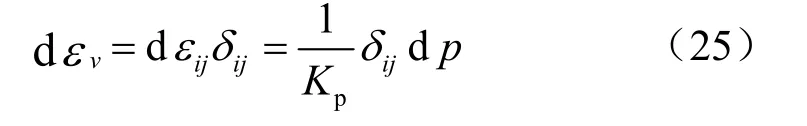
對于深部巖體來說，由于長期處于高地應力作用下，屬于密實介質，可以認為其具有體積模量K（K為常數），這是所能得到的巖體的最大體積模量。卸荷時，初始階段可能是彈性卸荷，而一旦其應力組合滿足屈服準則，則可能進入塑性階段，由于剪切變形的存在引起塊體的轉動，從而產生密實堆垛的破壞即擴容，從而引起體積模量的減小。卸荷模量Kp是一個變量，應當與巖石的破壞程度有關，目前還沒有Kp的詳細資料，只能通過實驗和插值給出，但明顯Kp＜K。

這樣可以計算由于開挖造成的指向圍巖開挖面的徑向應變：由于變形在徑向以外的方向的發展受到限制，因此，由于體積膨脹使得材料在徑向產生的應變為

由于彈性變形使得材料在r方向的應變值為

對式（28）進行無量綱化，可以得到

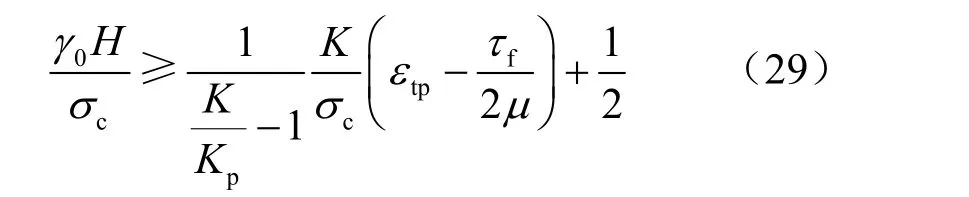
由式（30）可見，產生區域拉伸破碎的埋深條件與巖體的力學性質和破碎尺度密切相關。

4 結 論

（1）滑移剪切變形的發展將圍巖劃分成具有一定尺度的塊體（或條帶），它們之間的相互摩擦決定著殘余強度的大小。

（2）支護強度對不可恢復區峰值應力值影響不是很大，但對開挖面位移和不可恢復區半徑發展影響很大。當支護強度達到一定程度時，對這種影響逐漸減小，實際工程中應該選擇合適的支護強度以達到施工成本和支護效果的最大優化比。

（3）開挖卸荷使深部圍巖處于各向不均勻壓縮作用（大的軸向應力以及小的徑向應力）下，從而產生 “分層剝離”（拉伸破碎），分層剝離的存在使得圍巖開挖斷面監測到的位移大大超出按連續介質理論計算得到的數值。

（4）采用考慮擴容的計算模型可以得到圍巖產生區域拉伸破碎的條件，如果不考慮支護強度的影響，要使深地下開挖周圍圍巖產生不可恢復區的條件為式（20），而產生區域拉伸破碎的條件為式（30）。

[1] GURTUNCA R G, KEYNOTE L.Mining below 3 000 m and challenges for the South African gold mining industry[C]//Proceedings of Mechanics of Jointed and Fractured Rock.Rotterdam: BALKEMA A A, 1998.

[2] YERYOMENKO A A, GAIDIN A P, YERYOMENKO V A, et al.Features of technological block working in a rock-burst hazardous deposite[J].Journal of Mining Science, 2000, 36(6): 592－594.

[3] SHEMYAKIN E I, FISENKO G L, KURLENYA M V.Zonal disintegration of around underground workings,PartⅠ.Date of in situ observations[J].Journal of Mining Science, 1986, 22(3): 157－168.

[4] 錢七虎.深部巖體工程響應的特征科學現象及“深部”的界定[J].東華理工學院學報(自然科學版).2004,27(1): 1－5.QIAN Qi-hu.The characteristic scientific phenomena of engineering response to deep rock mass and the implication of deepness[J].Journal of East China Institute of Technology (Natural Science), 2004, 27(1):1－5.

[5] FENG Xia-ting.New rock mechanics development in China[C]//12th ISRM International Congress on Rock Mechanics.Beijing: [s.n.], 2011: 71－79.

[6] 何滿潮, 謝和平, 彭蘇萍, 等.深部開采巖體力學研究[J].巖石力學與工程學報, 2005, 24(16): 2803－2813.HE Man-chao, XIE He-ping, PENG Su-ping, et al.Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24(16): 2803－2813.

[7] HUDSON J A.The next 50 years of the ISRM and anticipated future progress in rock mechanics[C]//12th ISRM International Congress on Rock Mechanics.Beijing: [s.n.], 2011: 47－55.

[8] 錢七虎.巖土工程的第四次浪潮[J].地下空間, 1999,19(4): 267－272.QIAN Qi-hu.The fourth wave of geotechnology[J].Underground Space, 1999, 19(4): 267－272.

[9] 王明洋, 周澤平, 錢七虎.深部巖體的構造和變形與破壞問題[J].巖石力學與工程學報, 2006, 25(3): 448－455.WANG Ming-yang, ZHOU Ze-ping, QIAN Qi-hu.Tectonic, deformation and failure problems of deep rock mass[J].Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 448－455.

[10] 顧金才, 顧雷雨, 陳安敏.深部開挖洞室圍巖分層斷裂破壞機制模型試驗研究[J].巖石力學與工程學報, 2008,27(3): 433－438.GU Jin-cai, GU Lei-yu, CHEN An-min.Model test study on mechanism of layered fracture within surrounding rock of tunnels in deep stratum[J].Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 433－438.

[11] 謝和平, 鞠楊, 黎立云.基于能量耗散與釋放原理的巖石強度與整體破壞準則[J].巖石力學與工程學報, 2005,24(17): 3003－3010.XIE He-ping, JU Yang, LI Li-yun.Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3003－3010.

[12] 周小平, 錢七虎, 張伯虎, 等.深埋球形洞室圍巖分區破裂化機理[J].工程力學, 2010, 27(1): 69－75.ZHOU Xiao-ping, QIAN Qi-hu, ZHANG Bo-hu, et al.The mechanism of the zonal disintegration phenomenon around deep spherical tunnels[J].Engineering Mechanics, 2010, 27(1): 69－75.

[13] 周小平, 錢七虎.深埋巷道分區破裂化機制[J].巖石力學與工程學報, 2007, 26(5): 877－885.ZHOU Xiao-ping, QIAN Qi-hu.Zonal fracturing mechanism in deep tunnel[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 877－885.

[14] QI Cheng-zhi, WANG Ming-yang, QIAN Qi-hu.Evolution of the deformation and fracturing in rock masses near deep-level tunnels[J].Journal of Mining Science, 2009, 45(2): 112－119.

[15] 吳文平, 馮夏庭, 張傳慶, 等.深埋硬巖隧洞圍巖的破壞模式分類與調控策略[J].巖石力學與工程學報, 2011,30(9): 1782－1802.WU Wen-ping, FENG Xia-ting, ZHANG Chuan-qing,et al.Classification of failure modes and controlling measures for surrounding rock of deep tunnel in hard rock[J].Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1782－1802.

[16] JACGER J C, COOK N G.Fundamentals of rock mechanics[M].London: Chapman and Hall, 1979.

[17] 錢岳紅, 王德榮, 李杰, 等.掌子面前支撐壓力帶巖層變形破壞機制研究[J].巖土力學, 2011, 32(10), 3058－3064 QIAN Yue-hong, WANG De-rong, LI Jie, et al.Study of mechanism of rock mass deformation and failure ahead of working face on supporting zone[J].Rock and Soil Mechanics, 2011, 32(10): 3058－3064.

[18] 鄭穎人, 沈珠江, 龔曉南.巖土塑性力學原理[M].北京: 中國建筑工業出版社, 2002.