應力-溶解耦合作用下的鹽腔水溶建腔機制研究

湯艷春，周 輝，許 模

（1. 成都理工大學 地質災害防治與地質環境保護國家重點實驗室，成都 610059；2. 中國科學院武漢巖土力學研究所 巖土力學與工程國家重點實驗室，武漢 430071；3. 三峽大學 土木與建筑學院，湖北 宜昌 443002）

1 引 言

儲庫鹽腔一般采用水溶法建造，在水溶建腔過程中，控制合理的鹽腔形狀和尺寸一方面可以保證鹽腔有足夠的儲存容量，另一方面對于確保鹽腔圍巖的力學穩定性也是至關重要的。

前人圍繞巖鹽溶腔形態控制和穩定性及其相關特性，開展了大量和富有成效的研究工作。在巖鹽溶腔穩定性及其相關力學性質方面，HOU Zheng-meng[1]對地下工程開挖擾動區內巖鹽的力學和滲透性質進行了研究；LIANG等[2]對層狀鹽巖的力學特性進行了試驗研究；房敬年等[3]根據巖鹽單/三軸壓縮試驗和細觀力學試驗結果，對巖鹽的彈塑性損傷耦合機制進行了研究；張鵬等[4]利用彈塑性力學理論，對巖鹽溶腔頂板失穩機制進行了研究；尹雪英等[5－7]對儲氣庫長期穩定性進行了數值模擬計算和分析；楊強等[8]針對能源儲備地下庫群整體穩定性評價，運用考慮有限元強度折減法的變形穩定理論，建立了強度折減系數與塑性余能范數關系曲線的庫群整體穩定性和破壞的關鍵判據。在溶腔形態控制方面，班凡生等[9－10]、趙志成等[11]對巖鹽儲氣庫水溶建腔流體輸運理論以及溶腔形態變化規律進行了研究；霍琰等[12]對鹽穴建腔期腔內鹵水流場規律及夾層與流場的相互影響關系進行了研究。在巖鹽應力-溶解耦合機制研究及其相關性質方面，周輝等[13]建立了鹽巖裂隙滲流-溶解耦合模型，并通過試驗驗證了模型的適用性。湯艷春等[14－19]通過單軸壓縮條件下巖鹽應力-溶解耦合效應的細觀力學試驗以及三軸應力作用下巖鹽溶蝕特性試驗，對巖鹽應力-溶解耦合特性進行了分析，認為有無應力作用下的巖鹽溶蝕機制是一致的，兩者之間的差別在于溶蝕作用面積不同；溶蝕作用下巖鹽力學性質發生變化的機制在于巖鹽發生溶解使得巖鹽的宏觀力學參數發生了變化，但巖鹽破壞的力學機制并沒有本質上的改變；基于所提出的等效擴散系數的概念，建立了應力作用下的巖鹽溶蝕模型；在考慮黏聚力隨溶蝕作用發生變化的前提下，建立了溶蝕作用下巖鹽塑性力學模型。

目前所開展的大量研究工作忽略了巖鹽應力-溶解耦合效應對鹽腔水溶建腔過程的影響，這會對溶腔的形狀控制和力學穩定性分析結果造成不可忽略的誤差。本文通過巖鹽應力-溶解耦合效應對 鹽腔水溶建腔過程影響的分析，對應力-溶解耦合作用下的鹽腔水溶建腔機制進行研究，為進一步研究儲庫鹽腔水溶建腔機制提供理論依據和分析基礎。

2 應力-溶解耦合作用下的鹽腔水溶建腔機制

對于巖鹽溶蝕作用來說，應力的作用（特別是在產生塑性應變之后）對巖鹽溶蝕特性會產生非常明顯的影響，其影響是不可忽略的[14]。反過來，溶蝕作用也會對巖鹽的力學性質產生很大的影響，會使巖鹽的力學參數發生變化[16,19]，在實際鹽腔成腔過程分析中，必須考慮溶蝕作用下巖鹽力學性質的變化，因此，在鹽腔成腔過程的分析中必須要考慮應力與溶解的耦合效應對巖鹽水溶建腔的影響。

在鹽腔水溶建腔過程中，應力-溶解耦合作用下的鹽腔水溶建腔機制在于：一方面，在已具備的鹽腔形態條件下，鹽腔圍巖由于應力作用產生大量的裂紋，腔壁圍巖與水接觸后，水對裂紋和鹽腔表面產生溶蝕作用，并在鹽腔圍巖中形成一定的溶蝕影響范圍。在水的溶蝕影響范圍之內，腔壁圍巖由于溶蝕作用的影響，其在水的溶蝕影響范圍內的圍巖區域的巖鹽的力學性質發生變化，從而對整個鹽腔圍巖的應力場、應變場造成影響。另一方面，由于鹽腔邊界處圍巖力學性質的變化，水對鹽腔邊界處圍巖的溶蝕作用受到影響，鹽腔內部溶蝕過程發生改變，從而對鹽腔形態產生不可忽略的影響。

綜上分析可知，在鹽腔水溶建腔過程中，鹽腔形態以及鹽腔圍巖力學性質之間相互影響、相互制約。

3 應力-溶解耦合作用下的鹽腔水溶建腔計算方法

根據應力-溶解耦合作用下的鹽腔水溶建腔機制，針對實際的鹽腔水溶單井建腔工藝，建立應力-溶解耦合作用下的鹽腔水溶建腔計算方法。

3.1 計算思路

應力-溶解耦合作用下的鹽腔水溶建腔過程可采用如下計算思路：

①給定初始的鹽腔形態，對鹽腔圍巖的初始應力場、應變場進行計算，計算時采用溶蝕前圍巖介質巖鹽的力學性質參數。

②鹽腔圍巖與水接觸后，鹽腔圍巖受水影響范圍內的巖鹽力學性質參數發生變化。基于溶蝕作用下巖鹽塑性力學模型，對溶蝕作用下鹽腔圍巖進行力學計算。

③依據溶蝕后圍巖應力-應變分布，以及應力作用下的巖鹽溶蝕模型，進行應力作用下鹽腔形狀計算，獲取一定溶解時間之后的鹽腔形狀變化。第①～③步可合并稱為第一循環步。

④基于已改變的鹽腔形狀，以及溶蝕作用下巖鹽塑性力學模型，對鹽腔圍巖進行進一步的力學計算。繼而進行進一步的應力作用下鹽腔形狀計算。該步可稱為第二循環步。

⑤重復第二循環步的計算步驟，通過不斷的循環計算，即可得到應力-溶解耦合作用下的鹽腔水溶建腔過程。

3.2 計算模型的建立

3.2.1 模型的基本假設

考慮到計算的需要，可作簡化和基本假設：（1）忽略巖鹽結晶方向、層理等微構造的各向異性對溶蝕過程的影響，假設巖鹽是各向同性的均質材料。（2）不考慮巖鹽的流變特性等具時間效應的力學特性。（3）忽略溫度對巖鹽力學性質以及巖鹽溶蝕過程的影響。（4）假設巖鹽地層無雜質。（5）假設溶蝕過程中，鹽腔的腔體形態為軸對稱結構。（6）忽略地層傾角等地質因素對鹽腔水溶建腔過程的影響。（7）忽略初始地應力場對鹽腔初始形狀的影響。（8）假設在鹽腔內部進行溶解時，水影響范圍以外的巖鹽的力學性質不受水的影響。（9）假設鹽腔中流體運動為層流流動。

3.2.2 幾何模型

針對實際的單井鹽腔水溶建腔工藝，本文取如圖1所示的1/2物理模型進行計算。圖1中，鹽腔的初始形態為一球形，P0為上覆均布荷載； P1為側壓力；I代表鹽腔初始位置；II代表預定溶腔范圍線，所建立的坐標系原點在鹽腔的中心點。在圖 1中，由于所建立的計算模型的高度H較小，故可近似認為側壓力 P1為均布荷載。

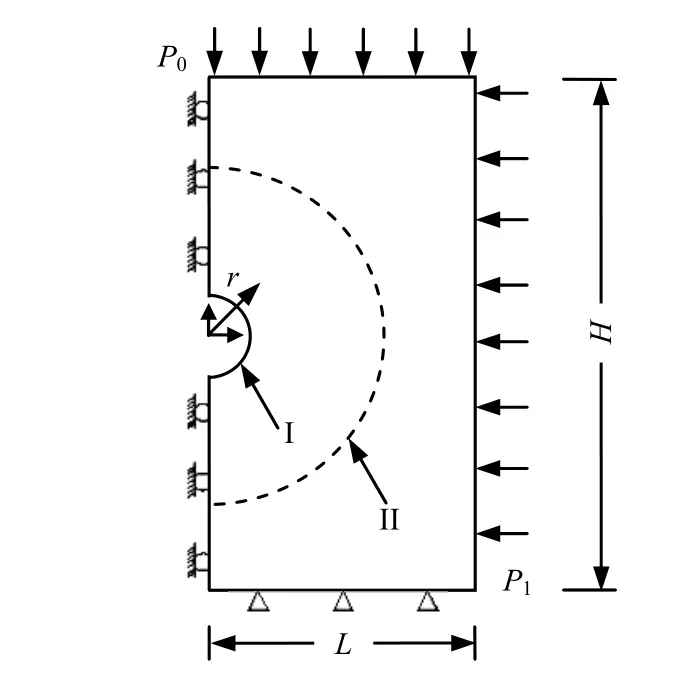
圖1 鹽腔幾何模型示意圖Fig.1 Sketch of geometrical model of rock-salt cavern

3.2.3 鹽腔圍巖區域網格劃分

對鹽腔圍巖區域網格劃分的規則如下：①沿鹽腔圍巖邊界，邊界網格均勻劃分。②鹽腔圍巖邊界網格的外法線方向過鹽腔的中心點。③在初始鹽腔至預定溶腔范圍線內部的區域，采用等間距的環向網格劃分方式進行網格劃分。

依照上述網格劃分規則，對鹽腔圍巖區域進行網格劃分，其網格劃分示意圖如圖2所示。

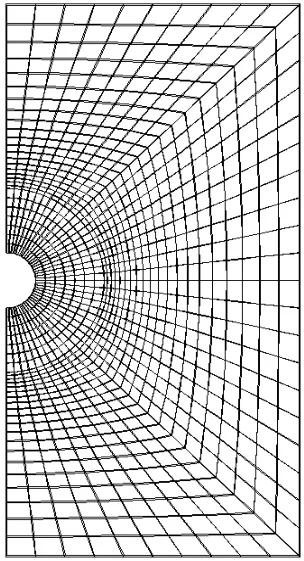
圖2 鹽腔圍巖區域網格劃分示意圖Fig.2 Meshing sketch of adjacent rock area of rock-salt cavern

3.3 計算步驟

為了計算應力-溶解耦合作用下的鹽腔水溶建腔過程，編制了有限差分計算程序來計算應力-溶解耦合作用下的鹽腔形態變化，以及不同溶腔形態時的圍巖應力場和應變場。具體計算步驟如下。

3.3.1 第一循環步的計算

（1）無溶蝕作用下巖鹽力學計算

給定初始的鹽腔形態，對鹽腔圍巖的初始應力場、應變場進行計算。采用的力學模型是應變硬化-軟化模型，應用FLAC計算軟件進行數值計算，黏聚力隨著等效塑性應變的變化可采用式（1）[16]中溶解前的計算公式來計算。

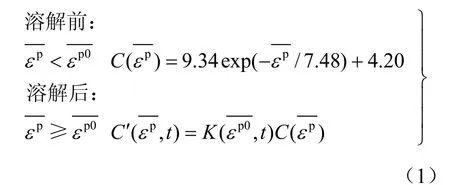
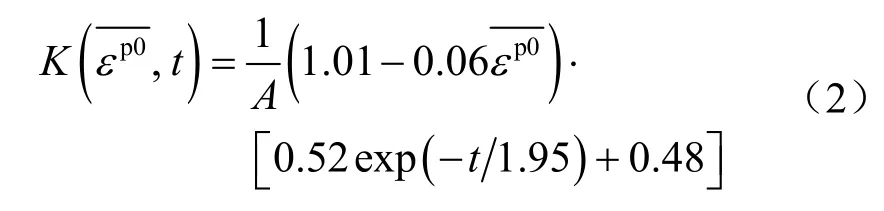
式中：A為常數，取為0.578。

（2）將鹽腔充滿水，忽略充水過程對鹽腔形狀的影響。

（3）溶蝕作用下巖鹽力學模型的計算

鹽腔圍巖與水接觸后，假定鹽腔圍巖受水影響范圍為鹽腔圍巖邊界單元。依據溶蝕作用下巖鹽塑性力學模型（該模型的假設條件、計算方法和參數等參考文獻[16]），對溶蝕作用下鹽腔圍巖進行力學計算，具體計算步驟：①改變鹽腔圍巖邊界單元的黏聚力參數值，在水影響作用范圍內的鹽腔圍巖邊界單元的黏聚力值采用式（1）中溶解后的黏聚力值計算公式來計算。②對于在水影響范圍以外的鹽腔圍巖單元，黏聚力值采用式（1）中溶解前的計算公式來計算。③使用FLAC計算軟件對鹽腔圍巖的應力場和應變場重新計算。④給出圍巖邊界單元的等效塑性應變值。

（4）應力作用下鹽腔形狀計算

基于所給出的圍巖邊界單元等效塑性應變值，將鹽腔內流體區域單獨考慮，近似模擬水溶建腔工藝，對鹽腔內流體區域的濃度場進行計算，進而可得到鹽腔形狀的變化。具體計算過程為

①建立鹽腔內流體區域計算模型

單獨考慮鹽腔內的流體區域，建立的計算模型如圖3所示。圖中，Ω為流體區域；Γ1為不溶邊界；Γ2為側溶邊界，即鹽腔圍巖邊界；A、B分別為Γ1和Γ2的交點。需要說明的是：側溶邊界Γ2的形狀隨著溶蝕作用而不斷變化。

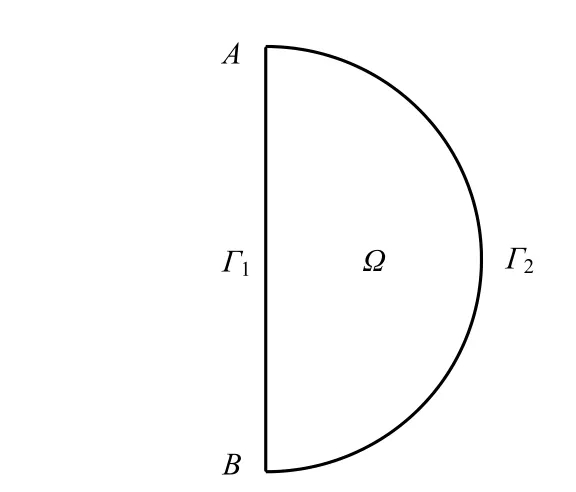
圖3 流體區域計算模型示意圖Fig.3 Sketch of fluid area model

在初始時刻(初始條件)，流體區域Ω內初始的濃度場C和速度場u均為0，可標記為

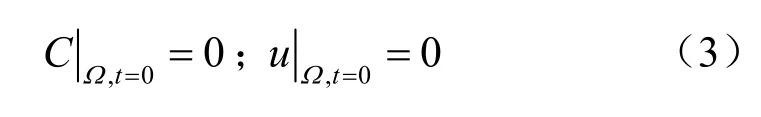
對于計算模型的邊界條件，速度邊界條件在鹽腔邊界表面上可取無滑移邊界條件，即

濃度邊界條件：溶蝕表面Γ2濃度取常數，即飽和濃度Cs；Γ1為不滲透邊界，可標記為

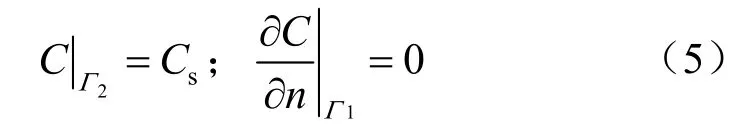
由于在側溶邊界上速度為 0，故可以采用單軸壓縮條件下巖鹽應力-溶解耦合效應的細觀力學試驗結果來計算鹽腔圍巖邊界上不同等效塑性應變下巖鹽的溶解速率。

②流體區域網格劃分

流體區域網格劃分與鹽腔圍巖區域的網格劃分不同，兩者只是共用一個鹽腔邊界；流體區域用四邊形網格進行劃分，靠近Γ1的區域網格小而密，遠離Γ2的區域網格大而疏。

③應力作用下鹽腔形狀計算

根據所給出的圍巖邊界單元的等效塑性應變值。鹽腔側溶邊界處的等效擴散系數 D*值（D*的概念是宏觀上單位時間內通過單位面積的質量流與法向濃度梯度的比例系數，用于描述應力作用下單位溶蝕面積上的宏觀溶蝕速率[15]）可由式（6）[15]確定。

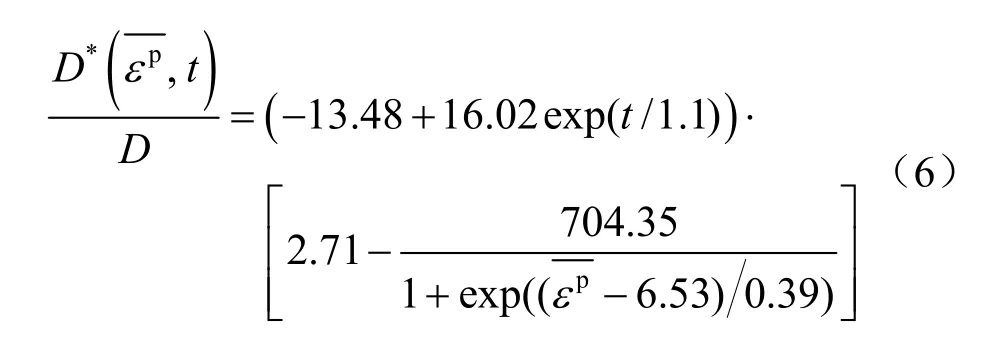
式中：無應力作用時巖鹽溶蝕的擴散系數D=2.0×10-9m2/s；為等效塑性應變（%）；t為溶解時間（100 s）。

將所確定的 D*值代入應力作用下巖鹽溶蝕模型中，對鹽腔內流體區域內濃度場進行計算，求得時間t內濃度場的變化（t為這一步中巖鹽溶解過程的總時間）。應力作用下巖鹽溶蝕模型的計算方法見參考文獻[15]。

鹽腔形狀計算。溶解厚度R與側溶邊界Γ2處濃度梯度之間的計算公式[15]為

根據式（7）可以計算出溶解t所溶解掉的R值，繼而求得側溶邊界Γ2的形狀變化。

物質平衡檢驗。根據物質平衡原理，對整個鹽腔流體計算區域進行總質量的守衡檢驗。假定在tn+1時刻進行質量守衡檢驗，定義相對誤差進行物質平衡檢驗：

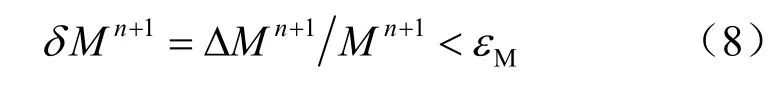
式中：εM為質量守衡許可誤差，如果計算出來的結果不符合式（8），則調整計算，控制和調整時間步長和單元大小； Mn+1為tn+1時刻實際計算的總質量值； ΔMn+1采用如下計算公式：

式中：M0為初始狀態的總質量；為 tn+1時刻流出的總質量；為tn+1時刻流入的總質量。

④溶解時間t的控制

溶解時間 t的選擇取決于所溶解掉的巖鹽厚度，當鹽腔側溶邊界處的溶解厚度R＞d時（d為圍巖邊界單元厚度），則認為鹽腔內流體的溶蝕計算停止，從而確定溶解時間t。

至此，第一循環步的計算結束，鹽腔圍巖的應力應變場以及鹽腔形狀已發生了變化。

3.3.2 第二循環步的計算

（1）導入第一循環步中計算出來的鹽腔形狀。

（2）進行溶蝕作用下鹽腔圍巖力學計算

計算過程：①將第一循環步中溶解掉的鹽腔圍巖邊界單元“開挖”，在 FLAC計算中對這些單元賦NULL，并算出此時圍巖中的等效塑性應變分布。②由于溶解“開挖”，鹽腔圍巖邊界發生了變化，變化后的鹽腔圍巖邊界單元的黏聚力值采用式（1）中溶解后的黏聚力值計算公式計算。③對于在水影響范圍以外的鹽腔圍巖單元，其黏聚力值采用式（1）中溶解前的計算公式來計算。④使用FLAC計算軟件計算出溶蝕作用下圍巖邊界單元的等效塑性應變值。

（3）進行應力作用下鹽腔形狀計算

基于上一循環步所計算出的鹽腔形狀，對鹽腔流體區域建立計算模型，劃分網格；基于溶蝕作用下圍巖邊界單元的值，采用式（6）確定鹽腔側溶邊界處的 D*值，根據應力作用下巖鹽溶蝕模型以及 D*值，對濃度場以及鹽腔形態進行計算，同時進行溶解計算中時間步長的控制以及物質平衡檢驗。

在第二循環步中，計算過程基本與第一循環步相同，假設條件、控制條件也與第一循環步相同。

緊接著的計算步驟就是第二循環步的重復，通過不斷地循環計算，就可以得到不同溶解時間下鹽腔形狀的變化。當鹽腔圍巖邊界達到預定的溶腔范圍線時，停止計算。

采用的應力-溶解耦合作用下的鹽腔形態變化計算程序流程圖見圖 4，溶蝕作用下鹽腔圍巖力學模型計算模塊的流程圖見圖 5，應力作用下鹽腔形狀計算模塊的流程圖見圖6。

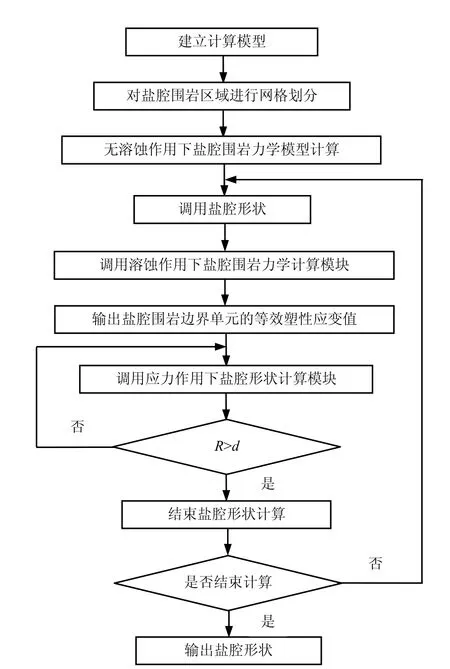
圖4 應力-溶解耦合作用下的鹽腔形態變化計算程序流程圖Fig.4 Flow chart of computing program of rock-salt cavern shape under coupled mechanical-dissolving effect

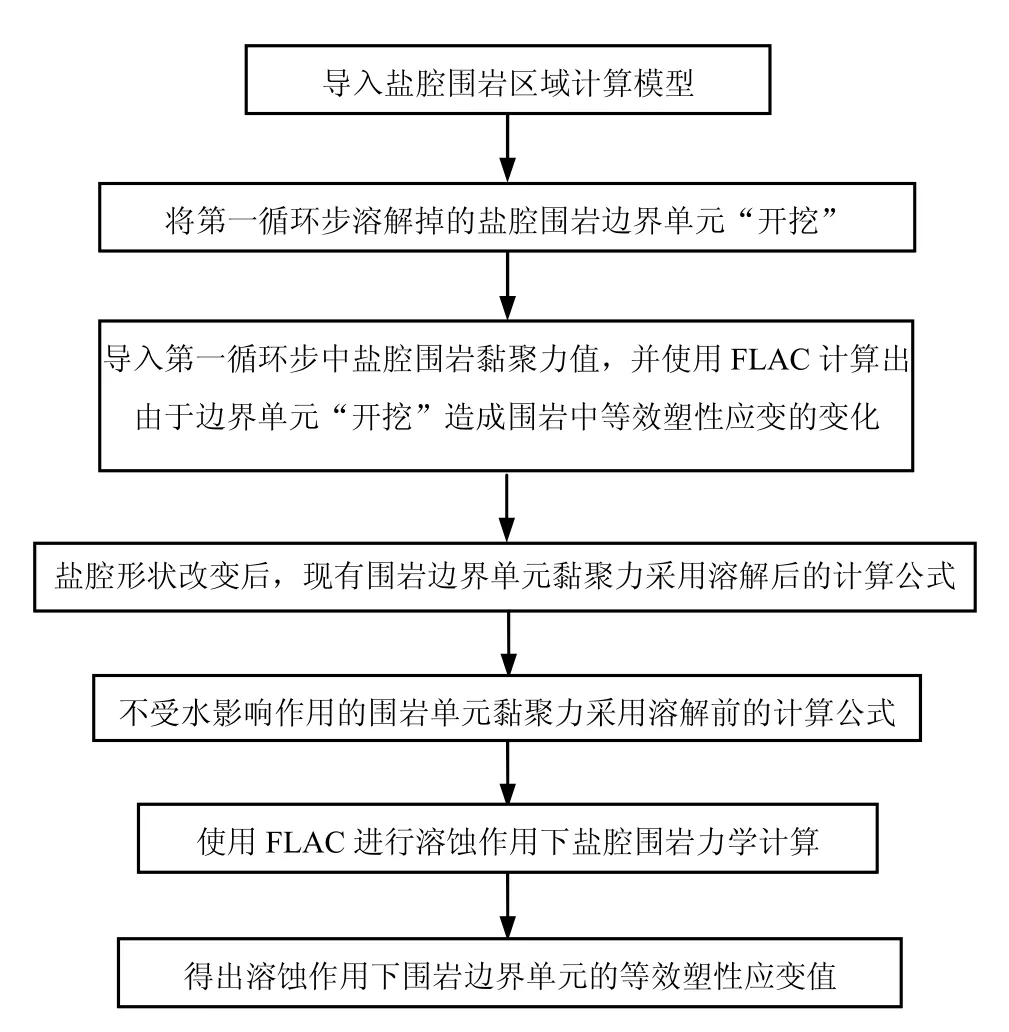
圖5 溶蝕作用下鹽腔圍巖力學計算模塊流程圖Fig.5 Flow chart of computing program of wall rock mechanical model under dissolving effect

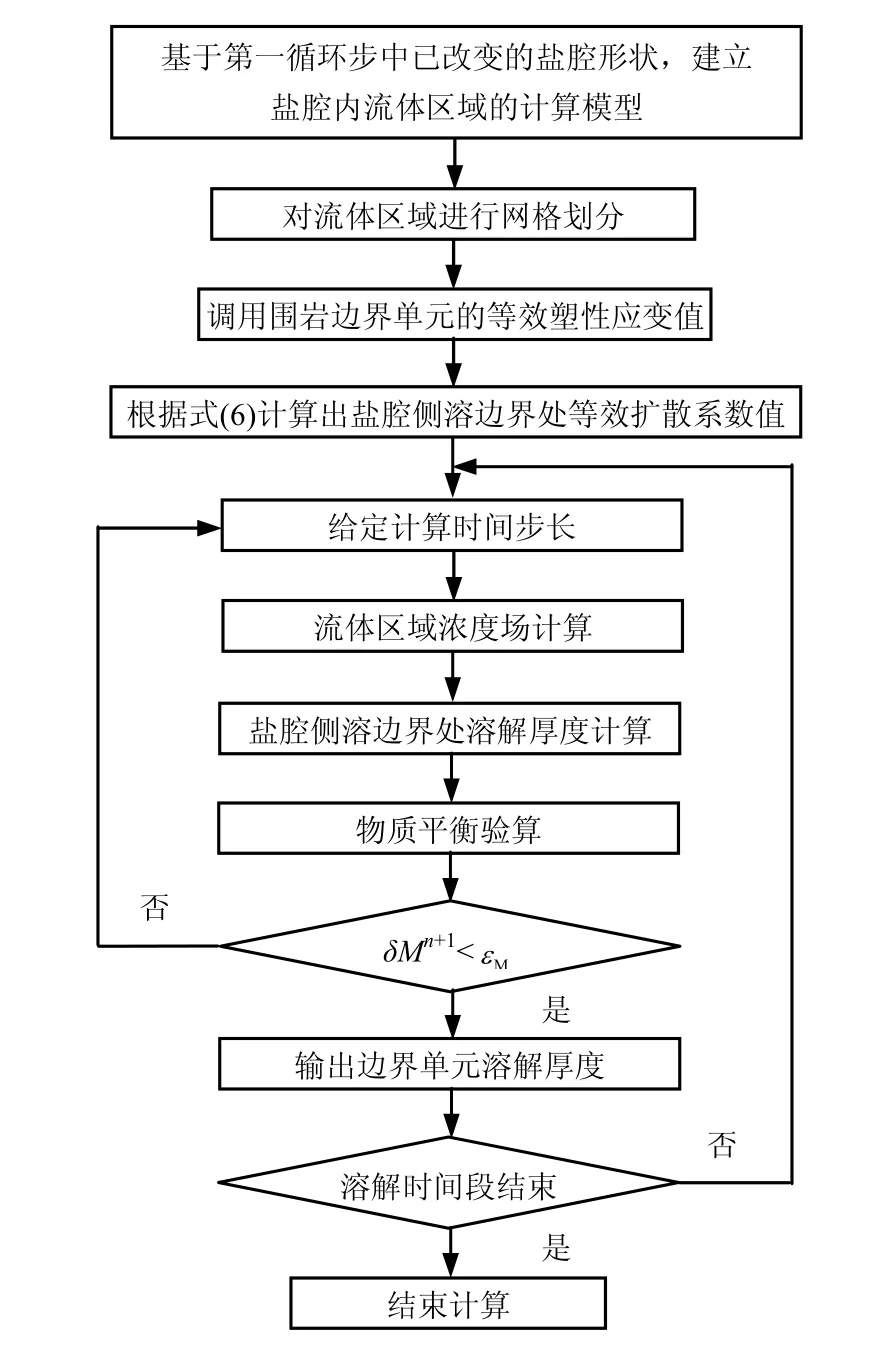
圖6 應力作用下鹽腔形狀計算模塊流程圖Fig.6 Flow chart of computing program of rock-salt cavern shape under mechanical effect

4 應力-溶解耦合與純溶解作用下鹽腔水溶建腔計算結果比較

為了更加清晰地反映應力-溶解耦合作用對鹽腔水溶建腔過程的影響，對應力-溶解耦合與純溶解作用下鹽腔水溶建腔的計算結果進行對比分析。

4.1 純溶解作用下鹽腔水溶建腔計算步驟

純溶解作用下鹽腔水溶建腔過程的計算在建立的計算模型、流體區域網格劃分，以及鹽腔內流體區域計算模型的初始條件、邊界條件和模型假設等方面，與應力作用下鹽腔形狀計算基本一致。兩者之間最主要的不同在于：在純溶解作用下鹽腔水溶建腔過程的計算中，鹽腔側溶邊界處擴散系數是相同的，都取純溶解狀態下的擴散系數D，其值不受應力因素的影響。純溶解作用下鹽腔水溶建腔過程的計算程序流程圖如圖7所示純溶解作用下鹽腔水溶建腔過程的具體計算步驟：

①建立純溶解作用下鹽腔內流體區域的計算模型，其初始的計算模型如圖3所示。

②調用鹽腔形狀。

③給定純溶解作用下鹽腔側溶邊界處的擴散系數D值，對每一個時間步長內鹽腔內流體區域的濃度場變化進行計算。

④計算鹽腔側溶邊界處的溶解厚度。

⑤得出鹽腔形狀。

⑥溶解時間步長以及物質平衡檢驗與上述應力作用下鹽腔形狀計算中的一致。

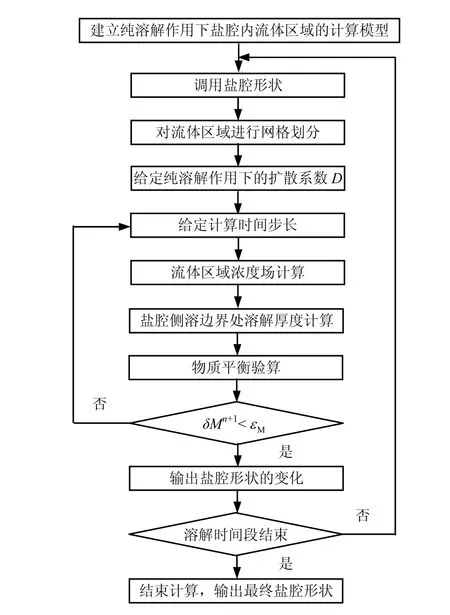
圖7 純溶解作用下鹽腔形狀計算程序流程圖Fig.7 Flow chart of computing program of rock-salt cavern shape under dissolving effect

4.2 計算結果對比

鹽腔計算模型的具體參數為：高度H = 60 m，寬度L = 30 m，初始鹽腔的半徑r = 2.5 m，預定鹽腔范圍線的半徑R = 10 m，上覆均布荷載P0= 25 MPa，側壓力P1= 30 MPa，巖鹽密度ρs= 2160 kg/m3。在初始溶腔和預定溶腔范圍線之內的區域，采用等間距的環向網格進行劃分，其厚度均為d = 20 cm。

通過應力-溶解耦合與純溶解作用下鹽腔水溶建腔計算，所取得的不同循環步時應力-溶解耦合與純溶解作用下鹽腔形狀變化如圖8所示，所取得的不同循環步時應力-溶解耦合作用下鹽腔圍巖區域的等效塑性應變分布變化如圖9所示。圖8中，綠色區域代表不同循環步時純溶解作用下鹽腔被溶解掉的區域，白色的區域與綠色區域之和代表不同循環步時應力-溶解耦合作用下鹽腔被溶解掉的區域，藍色區域則代表不同循環步時未溶解的圍巖區域。

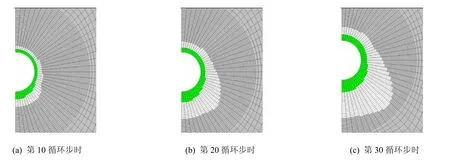
圖8 不同循環步時應力-溶解耦合與純溶解作用下鹽腔形狀變化Fig.8 Difference between rock-salt cavern shape at different cycle steps under coupled mechanical-dissolving effect and dissolving effect

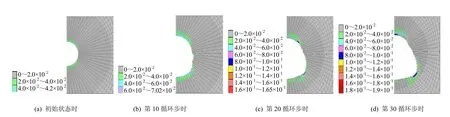
圖9 不同循環步時應力-溶解耦合作用下鹽腔圍巖區域等效塑性應變變化Fig.9 Difference between equivalent plastic strain of wall rock on rock-salt cavern under coupled mechanical-dissolving effect at different cycle steps

從圖8、9中可以看出，（1）隨著溶蝕作用的進行，鹽腔圍巖中的等效塑性應變分布發生了很大的變化，隨著鹽腔形狀的變化，在鹽腔形狀改變最大的地方，圍巖中的等效塑性應變也急劇變化。（2）在相同條件下，應力-溶解耦合作用下鹽腔的溶蝕速率比純溶解作用下鹽腔的溶蝕速率快，且在應力-溶解耦合作用下所溶解的巖鹽區域要比純溶解作用下所溶解的區域大。（3）隨著計算循環步的增加，鹽腔右下方的圍巖邊界單元的等效塑性應變發生明顯變化，并且使得應力-溶解耦合作用下鹽腔被溶解掉的區域（即白色區域）在右下方變化更為突出。造成該現象的原因是由于應力-溶解耦合作用下，首先由于初始狀態下圍巖邊界單元的等效塑性應變分布不同，造成不同圍巖邊界單元處溶蝕速率也不相同，從而使鹽腔形狀發生了改變；繼而，由于鹽腔形狀發生了改變，其圍巖邊界單元處的等效塑性應變分布也隨之發生改變。在等效塑性應變大的地方，溶蝕速率變大，使得此處溶腔形狀變化加大；而由于溶腔形狀變化加大，則此處發生應力集中，等效塑性應變值會變得更大，就會進一步加大此處溶腔形狀的變化。（4）應力-溶解耦合作用、純溶解作用下計算得到的鹽腔形狀，都為上小下大，但存在著較大的差別。純溶解作用下計算得到的鹽腔形狀為雞蛋狀，而應力-溶解耦合作用下計算得到的鹽腔形狀為梨形，并且比純溶解作用下計算得到的鹽腔的下端更扁更寬。

圖10為在應力-溶解耦合作用、純溶解作用下計算得到的鹽腔形狀與實際鹽腔形狀的對比圖。

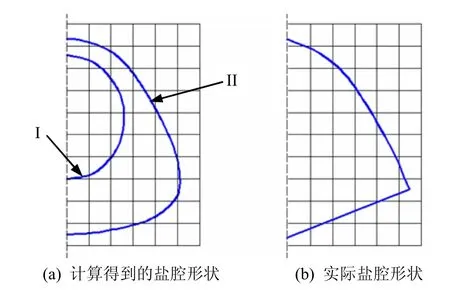
圖10 計算得到鹽腔形狀與實際鹽腔形狀對比Fig.10 Difference between computing rock-salt cavern shape

在圖10(a)中，曲線I為純溶解作用下計算得到的鹽腔形狀，曲線 II為應力-溶解耦合作用下計算得到的鹽腔形狀，圖中的豎向虛線代表中心軸。圖10(b)為實際溶腔形狀[5]，可見應力-溶解耦合作用下計算得到的鹽腔形狀與實際溶腔形狀較為符合。

5 結 論

（1）在鹽腔成腔過程中，應力-溶解耦合效應對鹽腔形狀的影響不可忽略。

（2）應力-溶解耦合作用下的鹽腔水溶建腔機理在于，由于溶蝕作用，在水的溶蝕影響范圍內的腔壁圍巖力學性質發生變化。同時，由于腔壁邊界處圍巖力學性質的改變，造成鹽腔內部溶蝕過程發生變化，從而使鹽腔形態發生改變。

（3）根據應力-溶解耦合作用下的鹽腔水溶建腔機理，針對實際的鹽腔水溶單井建腔工藝，建立了應力-溶解耦合作用下的鹽腔水溶建腔計算方法。

（4）使用編制的應力-溶解耦合作用下的鹽腔形態變化計算程序以及FLAC計算軟件對水溶建腔過程進行了計算，并對應力-溶解耦合作用、純溶解作用下計算得到的鹽腔形狀與實際鹽腔形狀進行了對比，發現應力-溶解耦合作用下計算得到的鹽腔形狀與實際溶腔形狀較為符合。

本文研究成果可為進一步研究儲庫鹽腔水溶建腔機制提供理論依據和分析基礎。

[1]HOU Zheng-meng. Mechanical and hydraulic behavior of rock salt in the excavation disturbed zone around underground facilities[J]. International Journal of Rock Mechanics and Mining Sciences,2003,40: 725－738.

[2]LIANG W G,YANG C H,ZHAO Y S,et al. Experimental investigation of mechanical properties of bedded salt rock[J]. International Journal of Rock Mechanics &Mining Sciences,2007,44(3): 400－411.

[3]房敬年,周輝,胡大偉,等. 巖鹽的彈塑性損傷耦合模型研究[J]. 巖土力學,待刊.FANG Jing-nian,ZHOU Hui,HU Da-wei,et al. Study of coupled elasto-plasto-damage model of rock salt[J]. Rock and Soil Mechanics,in press.

[4]張鵬,盧青峰,張文廣,等. 巖鹽溶腔頂板穩定性分析及其控制[J]. 中國井礦鹽,2011,42(3): 11－14.ZHANG Peng,LU Qing-feng,ZHANG Wen-guang,et al.Stability analysis and control of rock salt cavern roof[J].China Well and Rock Salt,2011,42(3): 11－14.

[5]尹雪英,楊春和,陳劍文. 金壇鹽礦老腔儲氣庫長期穩定性分析數值模擬[J]. 巖土力學,2006,27(6): 869－874.YIN Xue-ying,YANG Chun-he,CHEN Jian-wen.Numerical simulation research on long-term stability of gas storage in Jin-tan salt mine[J]. Rock and Soil Mechanics,2006,27(6): 869－874.

[6]戴永浩,陳衛忠,楊春和,等. 金壇鹽巖儲氣庫運營模型試驗研究[J]. 巖土力學,2009,30(12): 3574－3580.DAI Yong-hao,CHEN Wei-zhong,YANG Chun-he,et al.A study of model test of Jintan rock salt gas storage’s operation[J]. Rock and Soil Mechanics,2009,30(12):3574－3580.

[7]郤保平,趙陽升. 層狀鹽巖溶腔儲氣庫長期運行穩定性研究[J]. 地下空間與工程學報,2007,3(8): 1562－1567.XI Bao-ping,ZHAO Yang-sheng. Investigation on stability of gas storage caverns in bedded rock salt[J].Chinese Journal of Underground Space and Engineering,2007,3(8): 1562－1567.

[8]楊強,鄧檢強,呂慶超,等. 基于能量判據的鹽巖庫群整體穩定性分析方法[J]. 巖石力學與工程學報,2011,30(8): 1513－1521.YANG Qiang,DENG Jian-qiang,Lü Qing-chao,et al.Global stability analytical method of cavern group in salt rock based on energy criterion[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(8): 1513－1521.

[9]班凡生. 鹽穴儲氣庫水溶建腔優化設計研究[D]. 北京：中國科學院滲流流體力學研究所,2008.

[10]班凡生,耿晶,高樹生,等. 巖鹽儲氣庫水溶建腔的基本原理及影響因素研究[J]. 天然氣地球科學,2006,17(2): 261－266.BAN Fan-sheng,GENG Jing,GAO Shu-sheng,et al.Studying on basic theory and influence factor of gas storage in salt caverns building with water solution[J].Natural Gas Geoscience,2006,17(2): 261－266.

[11]趙志成,朱維耀,單文文. 鹽穴儲氣庫水溶建腔機制研究[J]. 石油勘探與開發,2003,30(5): 107－109.ZHAO Zhi-cheng,ZHU Wei-yao,SHAN Wen-wen.Research on mechanism of solution mining for building underground gas storage in salt cavern[J]. Petroleum Exploration and Development,2003,30(5): 107－109.

[12]霍琰. 鹽巖儲氣庫建腔期流場實驗研究及數值模擬[D].重慶: 重慶大學,2010.

[13]周輝,湯艷春,胡大偉,等. 鹽巖裂隙滲流-溶解耦合模型及試驗研究[J]. 巖石力學與工程學報,2006,25(5):946－950.ZHOU Hui,TANG Yan-chun,HU Da-wei,et al. Study of coupled penetrating-dissolving model and experiment for salt rock cracks[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(5): 946－950.

[14]湯艷春,周輝,馮夏庭,等. 單軸壓縮條件下巖鹽應力-溶解耦合效應的細觀力學試驗分析[J]. 巖石力學與工程學報,2008,27(2): 294－302.TANG Yan-chun,ZHOU Hui,FENG Xia-ting,et al.Analysis of meso-mechanical test of rock salt considering couple stress-dissolving effects under unixial compression[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(2): 294－302.

[15]湯艷春,周輝,馮夏庭,等. 應力作用下巖鹽的溶蝕模型研究[J]. 巖土力學,2008,29(2): 296－302.TANG Yan-chun,ZHOU Hui,FENG Xia-ting,et al.Study of dissolving model under effect of stress for rock salt[J]. Rock and Soil Mechanics,2008,29(2): 296－302.

[16]湯艷春,周輝. 溶蝕作用下巖鹽塑性力學模型研究[J].巖石力學與工程學報,待刊.TANG Yan-chun,ZHOU Hui. Study of rock salt plasticmechanical model with dissolving effect[J]. Chinese Journal of Rock Mechanics and Engineering,in press.

[17]湯艷春,房敬年,周輝. 三軸應力作用下巖鹽溶蝕特性試驗研究[J]. 巖土力學,待刊.TANG Yan-chun,FANG Jing-nian,ZHOU Hui. Study of rock salt dissolving characteristics test with triaxial stress effect[J]. Rock and Soil Mechanics,in press.

[18]TANG Yan-chun,ZHOU Hui. Experimental study of dissolving effect on mechanical characteristics of rock salt[C]//The 43rd US Rock Mechanics Symposium and 4th U.S.-Canada Rock Mechanics Symposium. Asheville:[s. n. ],2009.TANG Yan-chun,ZHOU Hui,XIONG Jun. Study on some phenomena of rock salt mechanical property test with dissolving effect[J]. Advanced Science Letters,2012,12: 299－303.