蒼嶺特長公路隧道地應力場反演分析

汪 波，何 川，吳德興,，耿 萍

（1.西南交通大學 地下工程系，成都 610031；2.浙江省交通規劃設計研究院，杭州 310006）

1 引 言

初始地應力場是影響地下工程圍巖應力、位移分布以及破壞形式的重要因素之一，是地下工程設計的基本指標，尤其在長大公路隧道中，利用的初始地應力場是否可靠將直接影響到工程設計與施工的可靠性與安全性。

隨著測試技術的發展以及先進測量儀器的推廣應用，人們已能獲得較為可靠的實測地應力值[1]。但由于場地和經費等原因，不可能進行大量的全面量測，測量成果在很大程度上反映的是當地的局部應力場，加之巖體應力場影響因素眾多，測量成果受到測量誤差的影響，使測量值有一定的離散性。因此，為了更好地滿足工程設計和施工的需要，在甄選現場可靠的實測地應力資料基礎上，結合工程區地質條件，同時考慮工程區域的地形地貌特點，提出了多種依據某種數學模式來推求初始應力場的方法[2－5]。這些分析方法根據研究手段的不同又分為①邊界荷載調整法；②應力函數法；③三維有限元回歸分析法；④基于人工神經網絡初始地應力場的三維反分析法等。實際應用中考慮到邊界調整法存在諸如分析時無規律可循，對解的惟一性沒有理論依據，解的收斂性也難于判斷。應力函數法用于有限元計算時求出的應力分量并不能惟一求出其所對應的位移等缺點，在區域應力場分析中并未廣泛采用[6－8]。而由郭懷志、馬啟超等提出的有限元數學模型回歸分析初始應力場的方法，由于在分析過程中引入數理統計中的多元回歸分析原理，使得該法相對于其他初始應力場的分析方法具有相對科學性、可靠性及解的惟一性等優點，其在我國水利水電行業得到了迅速推廣，并取得了較為理想的效果。但在我國公路隧道中由于受工程重要性及規模等限制，利用該法進行初始應力場的研究還相對較少，目前僅見于雪峰山隧道[9－10]等特大型工程中。有鑒于此，本文擬采用多元回歸分析手段，在甄選蒼嶺隧道現場可靠的實測地應力資料基礎上，結合工程區實際地質、地形條件，對整個隧道區域的初始地應力場進行反演分析，最終獲得隧道軸線方向上應力場分布狀況，為隧道開挖過程中圍巖穩定性研究提供基礎性資料。

2 蒼嶺隧道工程區地應力實測資料

2.1 現場實測地應力資料

蒼嶺隧道是浙江省境內的一座特長公路隧道，總長度約2×7500 m，為我國目前在建的最長公路隧道之一，隧道區巖性單一，大部分為熔結凝灰巖，夾少量的花崗斑巖，構造發育較輕微，從施工過程來看，影響較大的為出口附近 F4斷層，隧道最大埋深達768 m，在此條件下進行隧道開挖施工，地應力的大小與分布對隧道的穩定性將產生重要影響。

設計中為查明工程區的地應力大小、方向及地應力對隧道圍巖穩定的影響，在隧道軸線附近部位采用水壓致裂法完成了CS1、CS2和CS33個鉆孔的原位地應力測試工作，獲得了工程區隧道圍巖的地應力大小、方向等力學參數，如圖1、表1所示[11]。

由圖1、表1可以看出：

除地應力測孔2在124.6～127.0 m為斷層破碎帶，鉆進過程中涌水，說明斷層有一定儲水空隙或通道，距離斷層附近的地應力值不高，沒有比較明顯的應力集中區域外，其余應力值基本隨著孔深的增加而隨之增大。由3個印模段確定最大水平主應力方向分別為N58° W、和N70° W。

綜合上述3個鉆孔實測地應力資料可以看出，蒼嶺隧道工程區地應力總體呈現 SH＞Sh＞Sv的特征，兩個水平應力均大于垂直應力，水平主應力占主導地位。測孔附近的地應力場以NWW向擠壓為主。

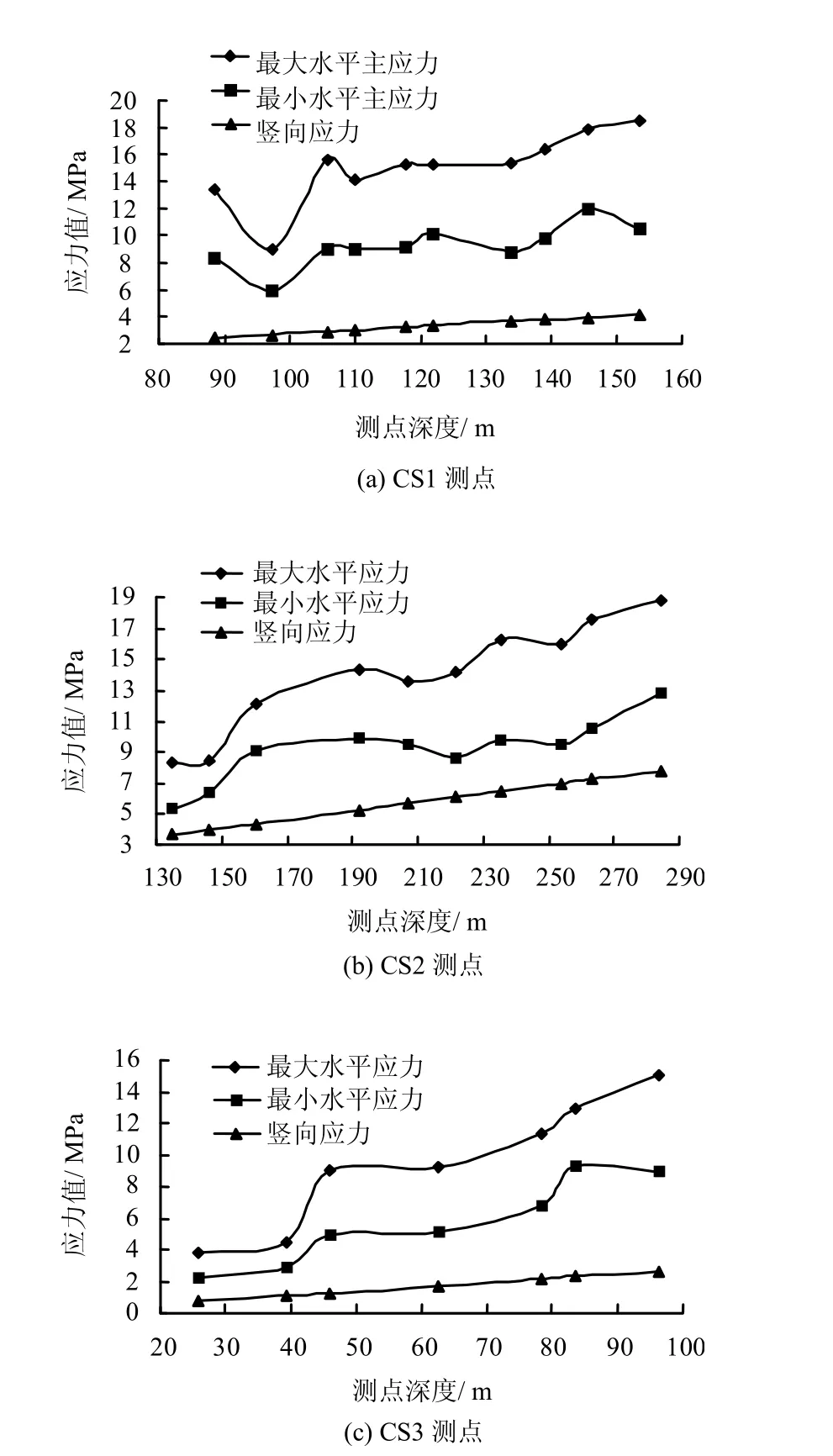
圖1 現場實測應力分布圖Fig.1 Curves of in-site measured stress distributions

表1 現場實測應力結果Table 1 Results of on-site measured stresses

2.2 地應力實測資料可靠性分析

由于地應力場成因復雜，影響因素眾多，加之受測量誤差影響，各測點實測數據的可靠性有待于進一步驗證，考慮到后續地應力場回歸分析以計算坐標系xyz中坐標應力分量為基本對象，而地應力實測值是按主應力平面方位和傾角給出，故需將實測地應力進行適當的坐標變換[12－13]（如表 2及式（1）所示）。

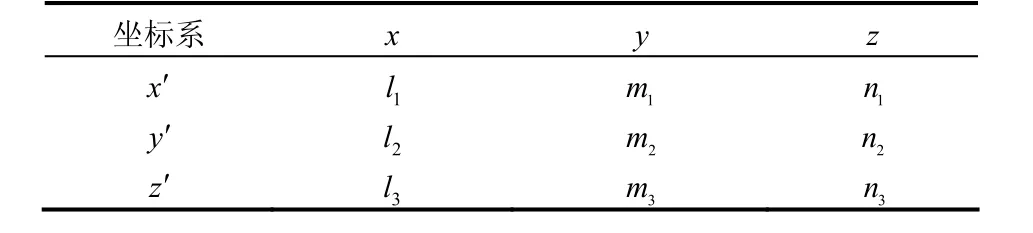
表2 不同坐標系方向余弦表Table 2 Direction cosine table in different coordinate systems

根據每組空間實測應力的量值和方位,，同時考慮到蒼嶺隧道實測過程中假定鉛直面內無剪應力存在，故利用式（1）進行坐標轉換后得到 Sx、Sy、Sz、Sxy4個應力分量，并據此獲得實測地應力特征參數換算成果如圖2所示。

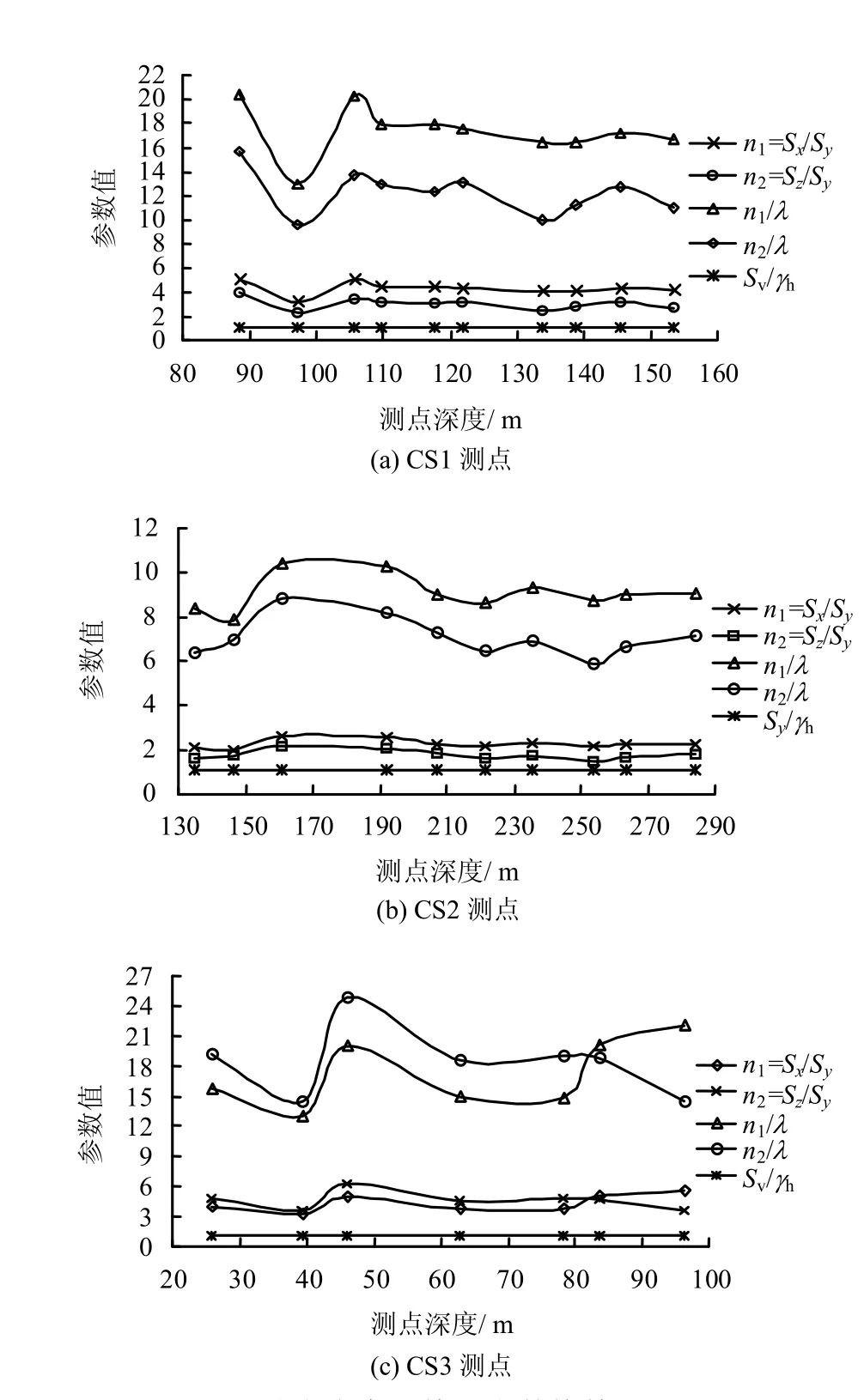
圖2 地應力實測特征參數換算成果圖Fig.2 Conversion results of characteristic parameters of insitu stresses of characteristic parameters of conversion plan

表3 地應力實測特征參數換算結果Table 3 Conversion results of characteristic parameters of in-situ stresses

從圖2、表3可以看出：

（1）隧址區地應力實測分量之間的關系總體上呈現出 Sx＞Sz＞Sy的特點。CS2測點附近n1、n2值明顯小于CS1、CS3測點處的相應值，說明該處由于受斷層帶影響而產生了應力松弛，故水平面內的應力值較小。且隧道軸線同大主應力方向基本一致。

（2）地應力實測值中的水平分量遠大于巖體自重泊松效應所形成的水平應力，隧道區存在一定地質構造作用，巖體地應力由自重與構造應力組成；從實測鉛直向應力Sy與上覆巖體自重形成的豎向應力γh對比關系看，比值均在1.1左右，表明實測鉛直向應力場與自重應力場基本一致。

（3）綜合比較CS1、CS3測點可知：此兩測孔處地質條件基本相當，受構造運動影響均較小，兩測孔處應力水平應相差不大，但從圖2中可以看出，CS3測點處n1、n2值的分布與CS1點處明顯不同，CS3點處n1、n2值分布至深度達85 m后才與CS1點趨于一致，造成此種差異的原因可能是由于CS3實測點位深度較淺，受淺表生改造作用所致[14]。同時CS1、CS2點處個別測點與同位置其他測點相比較也存在一定的差異（如CS1測孔處第2點、CS2測孔處第3、4點等）。綜合比選分析后，在后續的應力回歸過程中選取埋深大、實測應力相對較為穩定可靠的17個測點作為回歸對象。

3 工程區初始應力場反演回歸分析

3.1 計算范圍、模型及參數的確定

計算范圍的確定應遵循以下2個原則[13]：①幾何范圍必須包含全部工程影響區域，且適當增大，減少邊界影響。②邊界處的幾何約束條件易于確定，宜將山脊線與河谷線選作邊界，因其兩側地形大致對稱，可假定此類邊界條件不會在與邊界線垂直的方向上發生位移。通過分析蒼嶺隧道工程區的范圍、工程地質與水文地質條件以及地應力實測點的分布情況，在平面上，選擇了蒼嶺隧道線路附近約2600 m×8100 m的長方形區域作為主要計算區域，其中沿隧道軸線方向（長度方向，x軸方向）取8000 m，垂直于隧道線路軸線方向（寬度方向，z軸方向）取2600 m，在立面圖（高度方向，y軸方向）上，模型底面取自設計高程以下-200 m，頂面高程取實際地形高程擬合成三維的曲面。該計算區域從公路路線 K94＋410至K102＋830，包括蒼嶺隧道開挖全長；并且包含主要斷層在內。具體計算范圍及網格見圖3。

為了保證計算精度，又便于劃分單元，本次三維模型離散化全部采用 10節點四面體等參單元（Solid92）。在劃分有限元網格時，采用了不同精度的網格劃分：在對計算結果影響最大的主要計算區域采用了較高的網格密度，在輔助計算區域內采用了相對較低的網格密度，具體操作是在計算最為關心的CS1、CS2和CS3測孔附近、斷層破碎帶附近以及隧道軸線附近對網格進行了適當的加密。這樣的網格劃分既保證了計算精度，同時也控制了計算的規模。（網格剖分如圖3所示）。計算模型共計單元數189272個，節點數273468個。

隧道工程區巖性主要分為3種：一是分布最為廣泛的熔結凝灰巖；二是在進口附近分布的花崗斑巖，三是施工過程中揭露的對本隧道影響較大的F4斷層破碎帶，模型建立時考慮到斷層空間跨度大，在地層中的具體形態難以調查清楚，依據設計斷面圖取了一層厚度約為150 m的薄層來模擬斷層。計算中巖體材料參數的選取是在綜合參考蒼嶺隧道地質試驗資料和現場試驗的基礎上確定如表4所示。

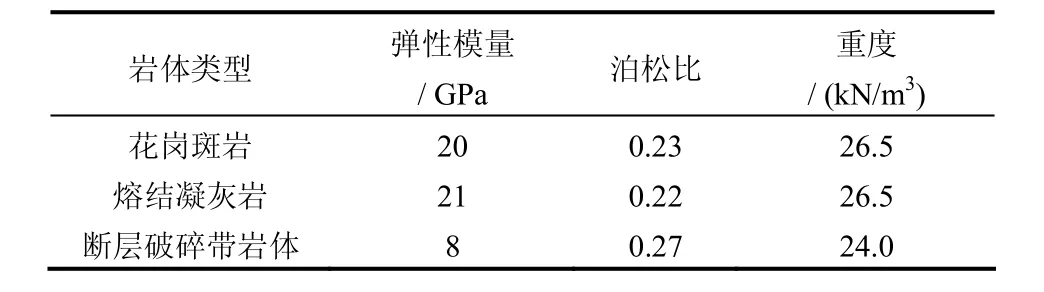
表4 巖體力學性質參數表Table 4 Mechanical parameters of rock masses

3.2 初始應力場反演回歸分析基本原理及其在蒼嶺隧道中實現過程

式中：σjk為第k觀測點j應力分量的觀測值；為i工況下k觀測點 j應力分量的有限元計算值；應力分量 j=1,2,… 6，對應6個初始應力分量，根據最小二乘法原理，使得殘差平方和Q為最小值的法方程式為

解此法方程式，得n個待定回歸系數 b=(b1, b2,…,bn)T，則計算區域內任意一點的回歸初始應力可由式（2）獲得，為衡量回歸效果，需進行前述的相關檢驗。

根據蒼嶺隧道實測地應力結果，將計算域內的地應力場視為自重應力場和邊界構造應力場的線性疊加，組合成蒼嶺隧道區域地應力場值。鑒于蒼嶺隧道水壓致裂法所測得的地應力結果無鉛直面內的剪切應力，在本次反演回歸中僅選取自重應力場和3個邊界水平構造應力場：即自重、東西及南北向擠壓構造和水平面內的剪切構造。計算中具體的實現過程如下：

（1）自重應力場：采用巖體實測重度，計算在自重作用下產生的自重應力場。

（2）構造應力場：在平面內，側面分別施加單位均布壓力來模擬東西、南北方向構造作用力,對水平面內剪切應力的模擬，依據文獻[9，15]，通過施加邊界位移來模擬。

3.3 蒼嶺隧道工程區應力場反演回歸結果分析

利用3個鉆孔共17個測點資料和4個三維有限元模擬地應力場結果，用最小二乘法多元回歸分析，得到分別對應自重應力、隧道軸線方向構造應力、垂直軸線方向構造應力和水平面內剪切應力的4個回歸系數 b1=9.0491，b2=-6.5334，b3=-3.6726，b4=2.2281和一個自由項 b0=2.9412，由此獲得形如式（5）的蒼嶺隧道工程區巖體的初始應力場回歸公式。

并利用相關公式得出復相關系數 r=0.8940，接近于 1，說明回歸的效果較好。偏相關系數V1=141.65，V2=305.97，V3=1681.77，V4=513.03，V5=19.58，偏相關系數中前4項均較大，說明所施加的各項分量對觀測數據的作用效果明顯，為不可剔除項，第5項偏相關系數雖相對較小，但由于該項反映隧道內的惟一剪應力影響項，綜合考慮構造應力影響后認為也不應剔除。同時利用式（5），獲得了實測各點應力分量的回歸值，并將其轉化為主應力值后與各實測點主應力值進行比較（如圖4所示）。

從圖中可以看出，實測與回歸的各主應力量值隨深度的總體變化趨勢是一致的，即呈增大的趨勢，3測點中豎向主應力回歸與實測值間擬合程度較好，基本趨于一致，這與豎向應力在水壓致裂法實測時的基本假定有關（見前述）；而水平主應力存在偏差，且這種偏差隨著測點深度、位置的不同而各異。總體而言，CS1位置處大部分測點SH、Sh實測值與回歸值吻合較好，僅在深度較大部位存在部分偏差，但最大差值不超過4 MPa；CS2部位各測點Sh實測值與回歸值擬合較好，但SH實測值與回歸值間存在較大差異；CS3各測點回歸值與實測值表現出與 CS2點相同的特征，最大差值達 5 MPa左右。造成上述差異的原因：一是水壓致裂法實測水平方向地應力的精度一般要低于自重方向；二是水平構造應力產生原因較為復雜，影響因素較多，特別是CS2、CS3測點處，前者位于斷層位置，后者則測深較淺，影響因素更為復雜。

從主應力之間的關系來看，回歸分析的主應力值同樣呈現出 SH＞Sh＞Sv的趨勢。同時將回歸獲得的各測點應力分量轉化為主應力作用方向可以看出，實測的 3個測點處最大主應力平均方位為N65.7° W，而回歸值中最大主應力平均方位為N67.04° W，二者較為接近。

綜合上述分析可知：回歸地應力值與實測值在量值上接近，變化趨勢基本相同，說明回歸得到的隧道區的應力場是合理的；同時，也進一步驗證了現場地應力量測結果。

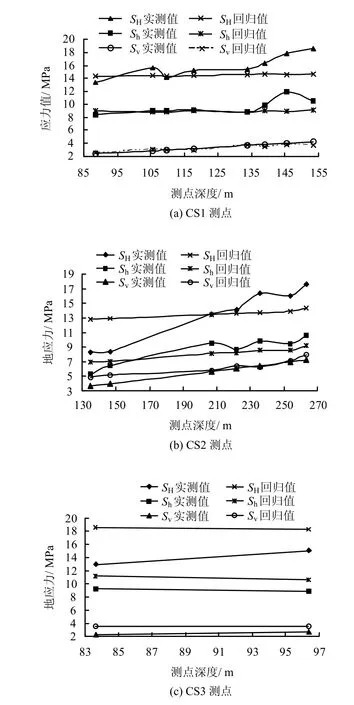
圖4 各測點主應力實測-回歸值-深度圖Fig.4 Curves of measured-regression value-depth of measured principal stresses for measured points

4 隧道軸線方向初始應力場分析

當求得回歸系數后，依據式（5），獲得了蒼嶺隧道線路軸線方向地應力場分布情況，并據此轉化為主應力值SH、Sh、Sv（如圖5所示）。

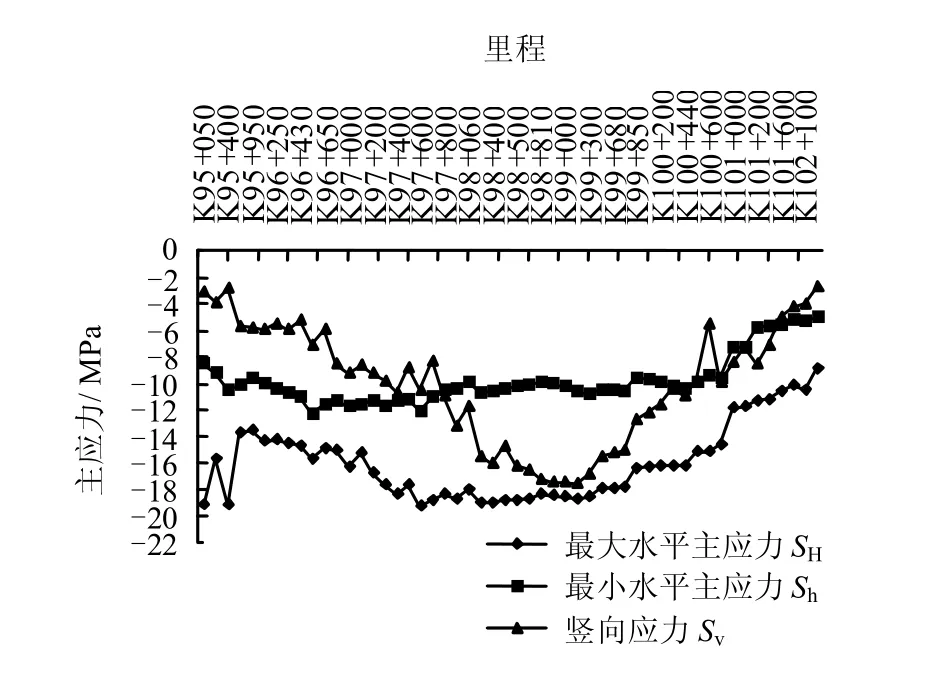
圖5 蒼嶺隧道軸線方向主應力場分布圖Fig.5 Principal stress field distribution of axis direction in Cangling tunnel

從圖中可以看出，隧道軸線上最大水平主應力較大值區域位于K97+300～K99+850附近，量值變化范圍為17.7～19.2 MPa；最小水平主應力的較大值位于K96+350～K97+700附近，量值變化范圍為10.7～12.3 MPa；自重應力場最大值位于K99+100附近，量值達17.6 MPa。縱觀隧道線路方向的主應力場變化規律可知，隧道軸線上的最大水平主應力值最初隨著埋深的增大而逐漸增加，但在K97+300后隨著埋深的增大幾乎保持不變，說明最大水平主應力場在隧道大埋深段基本處于穩定狀態，直至K99+700處產生了轉折，即此后隨著埋深的增加逐漸減小。以K98+200里程為臨界點，該里程點之前線路軸線方向的初始應力場中水平主應力占絕對主導地位，其量值上明顯大于以自重為主的豎向應力場；但在此里程之后，即K98+200～K99+700之間，隧道軸線上的初始應力場由最初的水平構造應力為主逐漸過渡為豎向的自重應力場與其相當，并在K99+100附近豎向自重應力場達到最大；隨后隨著里程的增加，又逐漸過渡到與初始進口段相同的應力水平，即以水平構造應力場為主。將隧道進出口附近回歸出的應力水平同水壓致裂法實測的CS1、CS3點處的應力水平對比可知，理論分析及實測結論相一致：即水平主應力值均明顯大于以自重應力場為主的豎向應力，再次說明了回歸結果的可靠性。分析中為避免邊界效應的影響，在上述隧道軸線的應力場分析中未考慮洞口段。

由于隧道線路在整個工程區域內的走向并不是直線，而是有轉折，因此，初始應力場中的最大主應力方向和隧道線路方向的夾角不是惟一的，具體如表5所示。

表5 最大主應力方向與隧道軸線間交角Table 5 Angles of the maximum principal stresses and tunnel axes directions

從上述大主應力與隧道軸線方向的夾角來看，二者交角在里程K100+793之前均較小，有利于隧道的穩定，在出口段交角較大，不利于隧道的穩定性，但有利的是該位置段主應力值相對較小，對隧道的穩定性影響相對也較弱。建議根據上述應力回歸結果進一步優化隧道線位走向，以期最大限度減少地應力場地不利影響。

5 結 論

（1）蒼嶺隧道工程區地應力總體呈現 SH＞Sh＞Sv的特征。測孔附近的地應力場以 NWW 向擠壓為主；

（2）綜合比選分析后選取埋深大、實測應力相對較為穩定可靠的17個測點作為最終回歸對象；

（3）比較回歸與現場實測值可知：主應力方向基本一致，主應力之間的分布關系大致相同，說明利用該法獲得的工程區初始應力場是較為合理的。但個別點差異較大。

（4）獲取了整個蒼嶺隧道軸線方向地應力場展布規律，并根據不同地段大主應力與隧道軸線方向的夾角對隧道穩定性狀況進行了分析，據此建議進一步優化蒼嶺隧道線位走向。

[1] 梅松華, 盛謙, 馮夏庭, 等. 龍灘水電站左岸地下廠房區三維地應力場反演分析[J]. 巖石力學與工程學報2004, 23(23): 4006－4011.MEI Song-hua, SHENG Qian, FENG Xia-ting. Back analysis of 3D in-situ stress field of undergroud powerhouse area of Longtan hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2004,23(23): 4006－4011.

[2] 艾凱. 地應力回歸分析與工程運用[J]. 礦山壓力與頂板管理, 2005, (8): 83－85.

[3] 豐定樣, 谷光榮, 楊家嶺, 等. 關于地下工程有限元分析中初始地應力場的假定[J]. 地下工程, 1982, (2): 20－27.

[4] 郭懷志, 馬啟超, 薛璽成, 等. 巖體初始應力場的分析方法[J]. 巖土工程學報, 1983, 5(3): 64－75.GUO Huai-zhi, MA Qi-chao, XUE Xi-cheng, et al. The analytical method of the initial stress field for rock masses[J]. Chinese Journal of Geotechnical Engineering, 1983, 5(3): 64－75.

[5] 朱伯芳. 巖體初始地應力反分析[J]. 水利學報, 1994,(10): 30－35.ZHU Bo-fang. Back analysis of initial stress in rock masses[J]. Journal of Hydraulic Engineering, 1994,(10): 30－35.

[6] 李永松, 尹健民, 艾凱, 等. 地應力回歸分析方法與工程應用實例[J]. 長江科學院院報, 2006, 23(4): 41－46.LI Yong-song, YIN Jian-min, AI Kai, et al. Unloading characteristic evaluation of Xiaowan hydropower station’s foundation rock mass by borehole elasticity modulus method[J]. Journal of Yangtze River Scientific Research Institute, 2006, 23(4): 41－46.

[7] 束加慶, 任旭華, 張繼勛, 等. 隧洞工程區三維初始地應力場的回歸分析[J]. 紅水河, 2006, 25(1): 46－49.SHU Jia-qing, REN Xu-hua, ZHANG Ji-xun, et al.Regression analysis of the 3D initial geostress field of tunnel project region[J]. Hongshui River, 2006, 25(1): 46－49.

[8] 戚藍, 丁志宏, 馬斌, 等. 初始地應力場多方程回歸分析[J]. 巖土力學, 2003, 24(增刊1): 137－139.QI Lan, DING Zhi-hong, MA Bin, et al. Regresstion analysis of initial in-situ stress field with multiple variables and equations[J]. Rock and Soil Mechanics,2003, 24(Supp. 1): 137－139.

[9] 邱祥波, 李術才, 李樹忱. 三維地應力場回歸分析方法與工程應用[J]. 巖石力學與工程學報, 2003, 22(10):1613－1617.QIU Xiang-bo, LI Shu-cai, LI Shu-chen. 3D geostress regression analysis method and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2003,22(10): 1613－1617.

[10] 朱光儀, 郭小紅, 陳衛忠, 等. 雪峰山公路隧道地應力場反演及工程應用[J]. 中南公路工程, 2006, 31(1): 71－75.ZHU Guang-yi, GUO Xiao-hong, CHEN Wei-zhong, et al.Inversion of in situ stress and its application to Xuefengshan roadway tunnel[J]. Journal of Central South Highway Engineering, 2006, 31(1): 71－75.

[11] 浙江省交通規劃設計研究院. 蒼嶺隧道施工圖設計工程地質勘察報告[R]. 杭州, 2004.

[12] 李莉, 何江達, 林正偉, 等. 糯扎渡水電站地下廠房初始地應力場研究[J]. 紅水河, 2003, 22(4): 28－32.LI Li, HE Jiang-da, LIN Zheng-wei, et al. Study on initial geostress of underground powerhouse of Nuozhadu power station[J]. Hongshui River, 2003, 22(4): 28－32.

[13] 楊林德. 巖土工程問題的反演理論與工程實踐[M]. 北京: 科學出版社, 1996: 314－349.

[14] 王蘭生. 地殼淺表圈層與人類工程[M]. 北京: 地質出版社, 2004.

[15] 張奇華, 鐘作武, 龔壁新. 施加邊界位移產生純剪應力及反分析應用[J]. 長江科學院學報, 2000, 17(2): 34－36.ZHANG Qi-hua, ZHONG Zuo-wu, GONG Bi-xin.Method of generating pure shear stress by adding boundary displacement and its application to back analysis for geostress field[J]. Journal of Yangtze River Scientific Research Institute, 2000, 17(2): 34－36.